Similar presentations:
Информатика
1.
ИнформатикаЛекции – 6 часов
Практические работы – 4 часа
Лабораторные работы – 4 часа
Экзамен
2. Литература
1.Гарибов, А. И. Информатика [Электронный ресурс] : учебное
пособие / А. И. Гарибов, Д. А. Куценко, Т. В. Бондаренко. —
Электрон. текстовые данные. — Белгород : Белгородский
государственный технологический университет им. В.Г. Шухова,
ЭБС АСВ, 2012. — 224 c. — 2227-8397. — Режим доступа:
http://www.iprbookshop.ru/27282.html
2.
Тушко, Т. А. Информатика [Электронный ресурс] : учебное пособие /
Т. А. Тушко, Т. М. Пестунова. — Электрон. текстовые данные. —
Красноярск : Сибирский федеральный университет, 2017. — 204 c.
— 978-5-7638-3604-2. — Режим доступа:
http://www.iprbookshop.ru/84360.html
3.
Системы счисленияСистема счисления - это совокупность приемов и правил
для записи чисел цифровыми знаками.
Числа записываются по определенным правилам с
помощью символов некоторого алфавита, называемых
цифрами.
системы счисления
позиционные
непозиционные
4.
Непозиционной называют систему счисления, в которой значениецифры не зависит от ее положения в числе.
− Единичная система счисления
III - число 3
− Римская система счисления
I
1
V
5
X
10
L
50
Например:
MCMLXXVIII = 1978
C
100
D
500
M
1000
5.
Позиционной называют систему счисления, в которой количественноезначение цифры зависит от ее положения в числе.
Пример: В десятичном числе 757,7 первая
семерка означает 7 сотен, вторая – 7
единиц,
третья – 7 десятых долей единицы.
Базис позиционной системы счисления – это последовательность
чисел, каждое из которых задает значение цифры по ее месту в записи
числа, т.е. вес каждого разряда.
Базис традиционных позиционных систем счисления
…, P3, P2, P1, P0, P-1, P-2, P-3,…
Основание (P) – знаменатель этой геометрической прогрессии.
Основание определяет количество цифр, используемых в этой системе
счисления.
6. Алфавит системы счисления – это совокупность цифр, используемых в этой системе. Если основание сиcтемы q<10, то в качестве
Алфавит системы счисления – это совокупность цифр, используемых вэтой системе.
Если основание сиcтемы q<10, то в качестве алфавита используют
первые q арабских цифр, если q>10, то в качестве алфавита используют
10 арабских цифр и (q-10) первых латинских букв.
Основание
Система
Алфавит
q=2
Двоичная
01
q=4
Четверичная
0123
q=8
Восьмеричная
01234567
q=16
шестнадцатеричная
0123456789ABCDEF
A – 10; B – 11; C – 12; D – 13; E – 14; F – 15.
7.
В общем случае любое число A в позиционной системесчисления с основание q можно представить в виде:
an-1qn-1 + an-2qn-2 + …+a1q1 + a0q0 + a-1q-1 +…+ a-mq-m
Где
q – основание системы счисления;
qi – вес i-го разряда;
ai – цифры системы счисления;
n – число целых разрядов;
m – число дробных разрядов.
Такая запись называется развернутой формой записи числа
(полиномом разложения).
an-1an-2a1 a0 ,a-1 +…+ a-m – сокращенная запись данного числа в
системе счисления с основанием q.
Примеры:
q=8
q=2
3111,0248
11,112
n=4
n=2
m=3
m=2
8. Правило перевода чисел из любой позиционной системы счисления в десятичную AqA10
Правило перевода чисел из любой позиционнойсистемы счисления в десятичную
Aq A10
Переводимое число необходимо записать в виде суммы
произведений цифр числа на основание системы счисления в
степени, соответствующей позиции цифры в числе.
5 4 3 2 1 0 -1 -2
111000, 112=1 25+1 24+1 23+1 2-1+1 2-2 =
= 32 + 16 + 8 + ½ + ¼ = 56,7510
421,58 = 4 82+2 81+1 80+5 8-1 = 256 + 16 + 1 + 5/8 =
273,62510
A7,C16 = 10 161+7 160+12 16-1 = 160 + 7 + 12/16 =
167,7510
9.
Правило перевода целых десятичных чисел всистему с основанием q
A10 Aq
1) последовательно выполнять деление данного числа и
получаемых целых частных на основание новой системы счисления
до тех пор, пока не получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой
системе счисления, привести в соответствие с алфавитом новой
системы счисления;
3) составить число в новой системе счисления, записывая его,
начиная с последнего полученного остатка.
10.
an–1 qn–1+an–2 qn–2+… a1 q1 +a0q
an–1 qn–1+an–2 qn–2+… a1
q
an–1 qn–1+an–2 qn–2+… a2
q
= an–1 2n–2 +…+ a1 (остаток a0)
= an–1 2n–3+…+ a2 (остаток a1)
= an–1 2n–4 +…+ a3 (остаток a2)
...
На n-м шаге получим набор цифр: a0a1a2…an–1
11.
Перевод чисел в двоичную системусчисления
363 181 90
45
22
11
5
2
1
1
1
0
1
1
0
1
1
0
36310 = 1011010112
28
27
26
25
24
23
22
21
20
256 128 64
32
16
8
4
2
1
4210 = 1010102
1710 = 100012
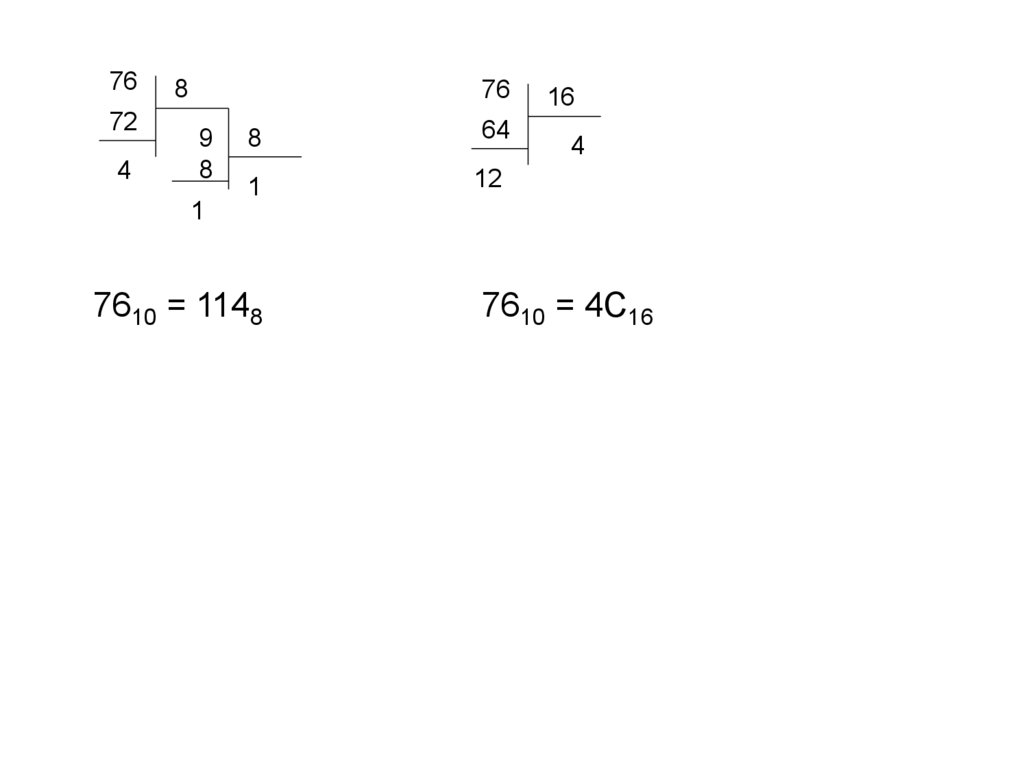
12.
7672
4
8
76
9
8
8
64
1
12
16
4
1
7610 = 1148
7610 = 4С16
13.
Правило перевода дробной части числа издесятичной системы в систему с основанием q
A10 Aq
Дробную часть числа умножаем на q, после чего целая часть запоминается и
отбрасывается. Полученная дробная часть умножается на q и т.д. Процесс
продолжается до тех пор, пока дробная часть не станет равной 0. Целые
части, выписываются после запятой в порядке их получения. Результатом
может быть либо конечная, либо бесконечная дробь. Во втором случае
обрывают умножение на каком-либо шаге и получают приближенную запись
исходного числа в системе с основанием q.
0,37510 A2
0,6510 A4
0 375
0 75
1 5
1 0
0,37510=0,0112
x2
0 65
x4
2 6
2 4
1 6
0,6510=2(21)4
14. Перевод Ap Aq
Перевод Ap AqЕсли p=qk (k>1, целое число), тогда при переводе чисел из системы с
основанием p в систему с основанием q каждую цифру в системе с
основанием p заменяют k цифрами в системе с основанием q (k-значным
числом).
16=24
При переводе чисел из шестнадцатеричной системы в двоичную каждой
шестнадцатеричной цифре ставится в соответствие 4 двоичные цифры
(двоичная тетрада), а при обратном преобразовании каждой двоичной
тетраде ставится в соответствие 1 шестнадцатеричная цифра. Тетрады в
двоичном числе отсчитываются от запятой вправо и влево.
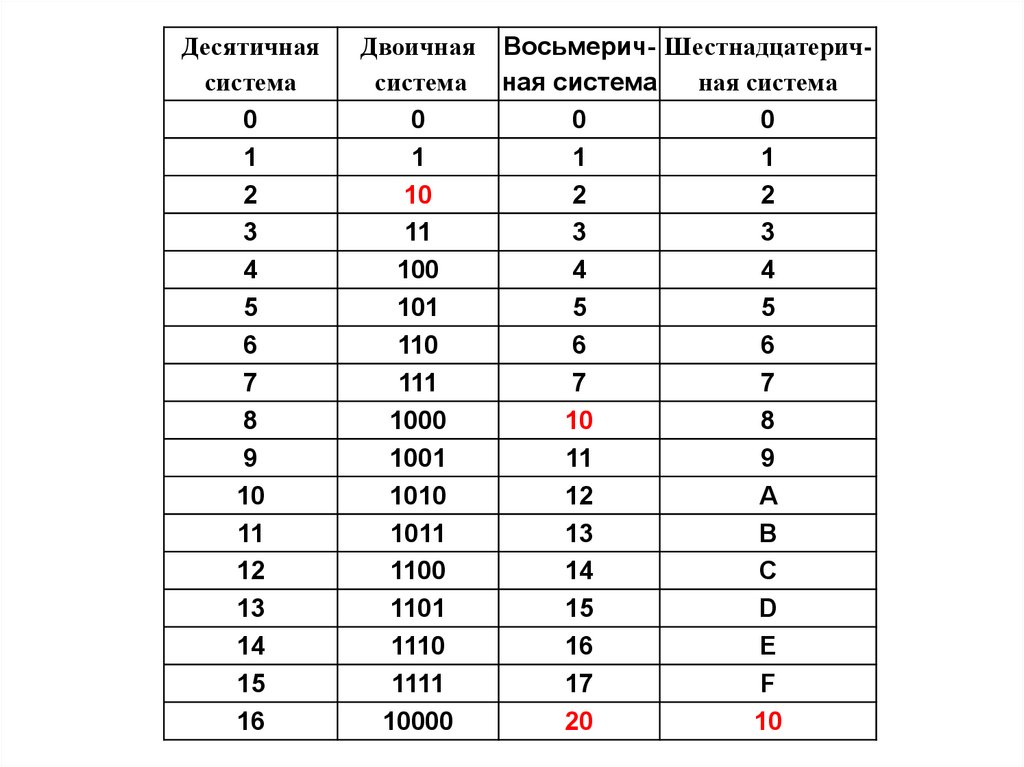
15.
Десятичнаясистема
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Двоичная
система
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
10000
Восьмерич- Шестнадцатеричная система
ная система
0
0
1
1
2
2
3
3
4
4
5
5
6
6
7
7
10
8
11
9
12
A
13
B
14
C
15
D
16
E
17
F
20
10
16.
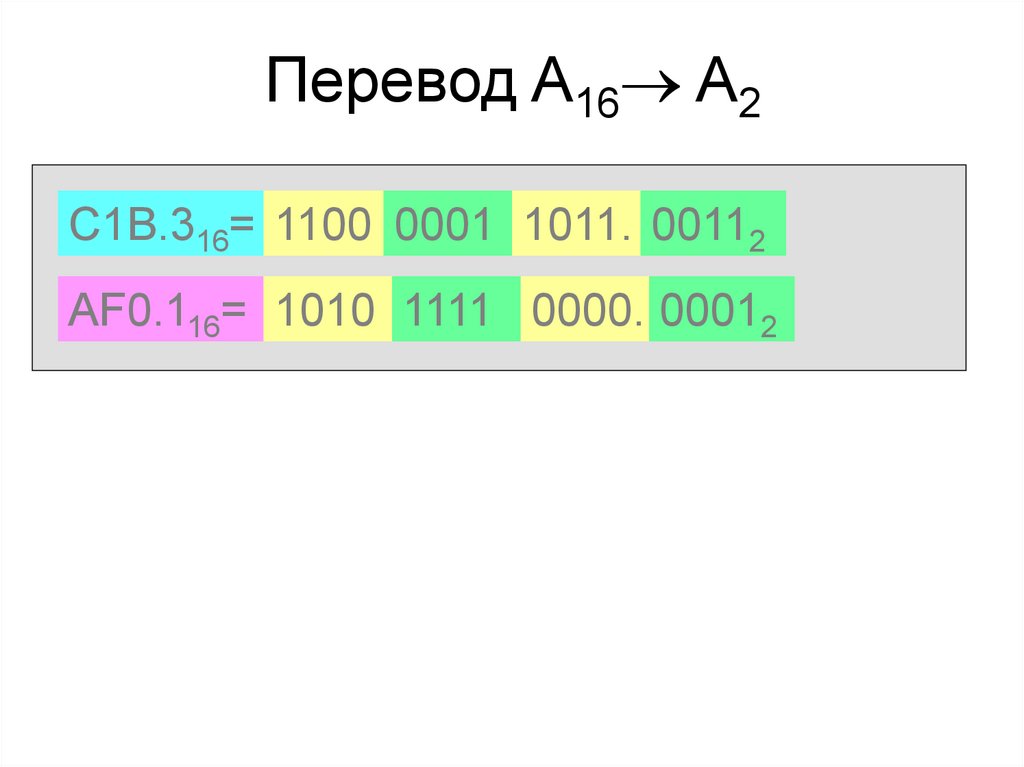
Перевод A16 A2C1B.316= 1100 0001 1011. 00112
AF0.116= 1010 1111 0000. 00012
17.
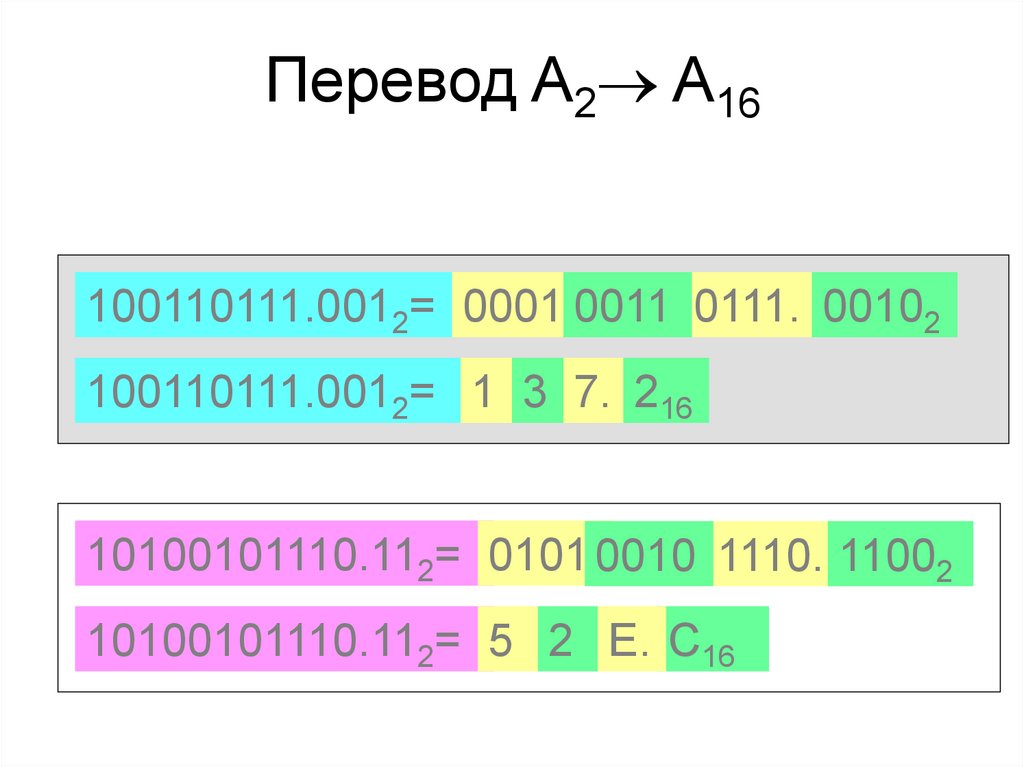
Перевод A2 A16100110111.0012= 0001 0011 0111. 00102
100110111.0012= 1 3 7. 216
10100101110.112= 0101 0010 1110. 11002
10100101110.112= 5 2 Е. С16
18.
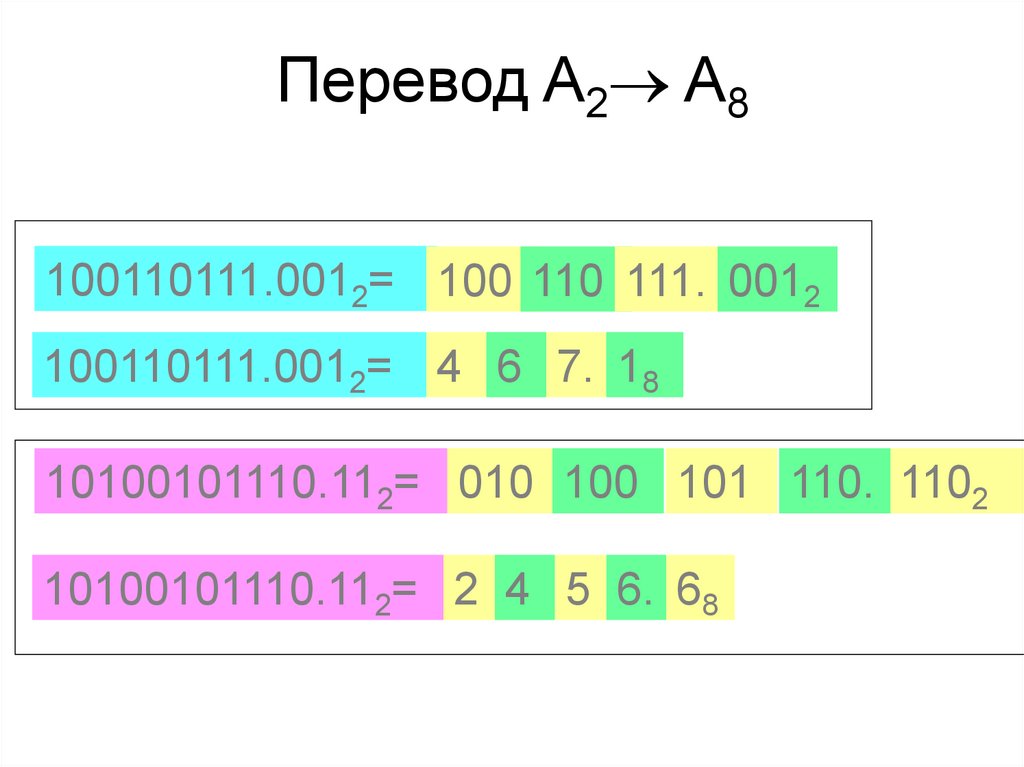
Перевод A2 A8100110111.0012= 100 110 111. 0012
100110111.0012= 4 6 7. 18
10100101110.112= 010 100 101 110. 1102
10100101110.112= 2 4 5 6. 68
19.
Перевод A2 A874.68= 111 100. 1102
310.58= 011 001 000. 1012
20.
Двоичная арифметикаСложение
Вычитание
0
1
1
+ 0
+ 0
+ 1
0
1
1 0
-
0
0
0
-
1
0
переносы
1
1
1
1
1
1
1 1 0 1 0 0 1 1
Число 1
1 1 0 1 1 1
Число 2
Сумма
1 0 0 0 0 1 0 1 0
Сумма
1 0
1
1
1
2
0
1
2
1 1 0 1 0 0 1 1
Число 1
Число 2
-
0
0
заем 1
+
1
1
заем 2
1
1
-
-
1 1 0 1 1 0
1 0 0 1 1 1 0 1
21.
Двоичная арифметикаУмножение
1 1 1 1 0
1 1 1 0
0 0 0 0 0
+
1+1
1
1
1 1
1 1 1 1 0
Деление
1 0 0 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1
1 0 1 1 1 1
1 1 0 0 0 1
1 1 0 0 0 1
1 0 1 1 1 1
1 1 1 1 0
1 0 1 1 1 1
1 1 1 0
1 0 1 1 1 1
0 1 0 0 1 0 0
0
22.
Арифметика в восьмеричной ишестнадцатеричной системах
счисления
q=16
A 0 C 6 1
A 0 C 6
1
+ 2 8 F D 7
- 2 8 F D 7
C 9 C 3 8
7 7 C 8 A
q=8
+
7 0 0 6 1
7 0 0 6 1
2 7 6 5 4
- 2 7 6 5 4
1 1 7 7 3 5
4 0 2 0 5
23.
Двоично-десятичная системасчисления (BCD 8421)
Десятичная
цифра
Двоичнодесятичный
запись
0
0000
1
0001
2
0010
3
0011
4
0100
5
0101
Неупакованное число
6
0110
173=0011 0001 0011 0111 0011 0011
7
0111
8
1000
9
1001
Используется в цифровых
устройствах ввода-вывода
числовой информации.
1001 0101 0011 10002=38200
1001 0101 0011 10002-10=9538
Упакованное число
173= 0001 0111 0011
24.
Сложение двоично-десятичных чисел+
0 1 1 0
0 0 1 1
0 1 1 1
0 1 1 0
6 3 7 6
+ 0 0 0 1
1 0 0 0
1 0 0 0
1 0 0 1
1 8 8 9
0 1 1 1
1 0 1 1
1 1 1 1
1 1 1 1
0 1 1 0
0 1 1 0
0 1 1 0
1
1
1
1 0 0 0
0 0 1 0
0 1 1 0
8 2 6 5
0 1 0 1
Вычитание двоично-десятичных чисел
-
6 3 7 6
1 8 8 9
4 4 8 7
-
0 1 1 0
0 0 1 1
0 1 1 1
0 1 1 0
0 0 0 1
1 0 0 0
1 0 0 0
1 0 0 1
0 1 0 0
1 0 1 0
1 1 1 0
1 1 0 1
0 1 1 0
0 1 1 0
0 1 1 0
0 1 0 0
1 0 0 0
0 1 1 1
25.
Представление целых чиселЦелые числа могут представляться в компьютере со знаком
или без знака.
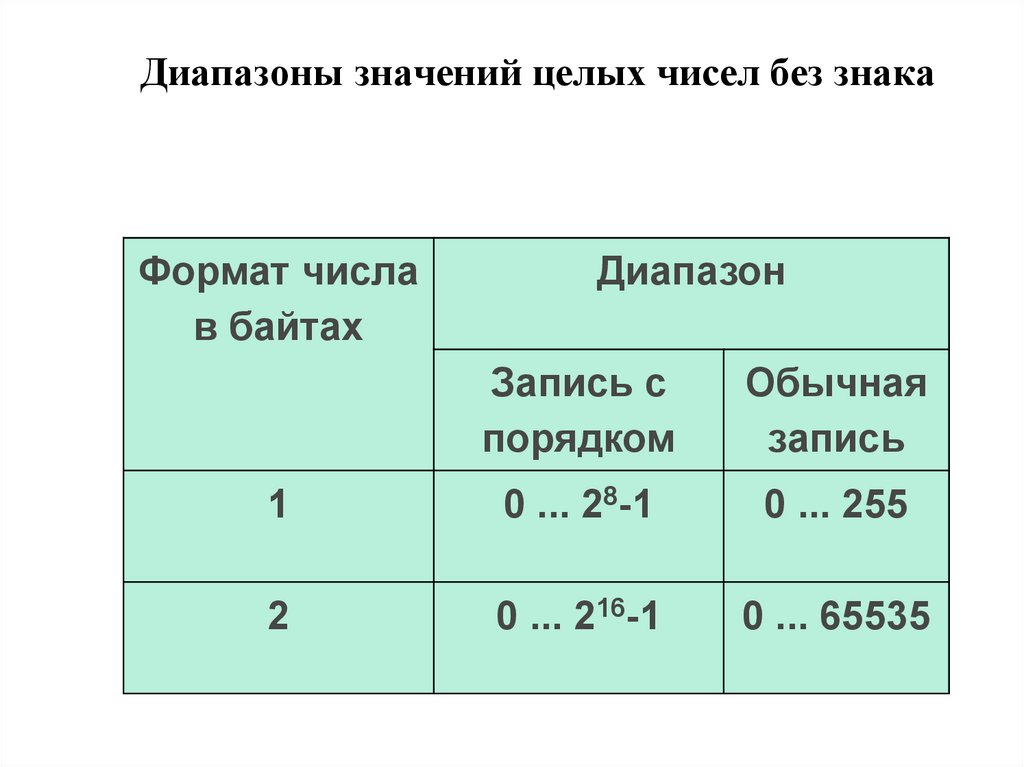
Целые числа без знака обычно занимают в памяти один
или два байта и принимают в однобайтовом формате
значения от 000000002 до 111111112 , а в двубайтовом
формате - от 00000000 000000002 до 11111111111111112.
26.
Диапазоны значений целых чисел без знакаФормат числа
в байтах
Диапазон
Запись с
порядком
Обычная
запись
1
0 ... 28-1
0 ... 255
2
0 ... 216-1
0 ... 65535
27.
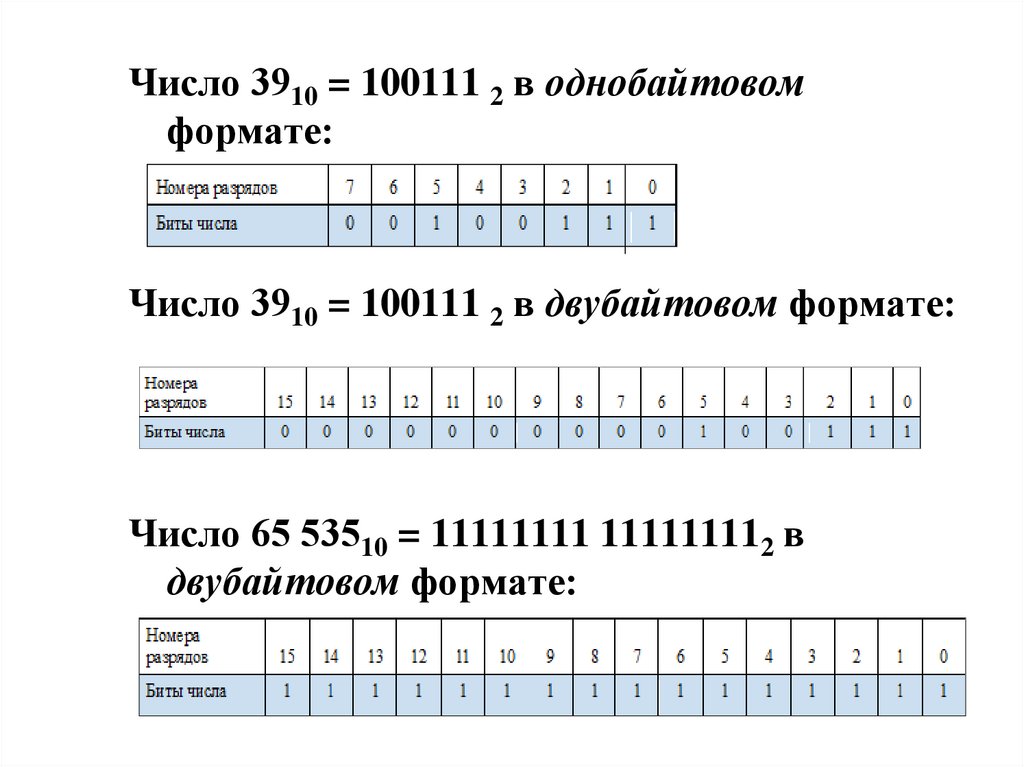
Число 3910 = 100111 2 в однобайтовомформате:
Число 3910 = 100111 2 в двубайтовом формате:
Число 65 53510 = 11111111 111111112 в
двубайтовом формате:
28.
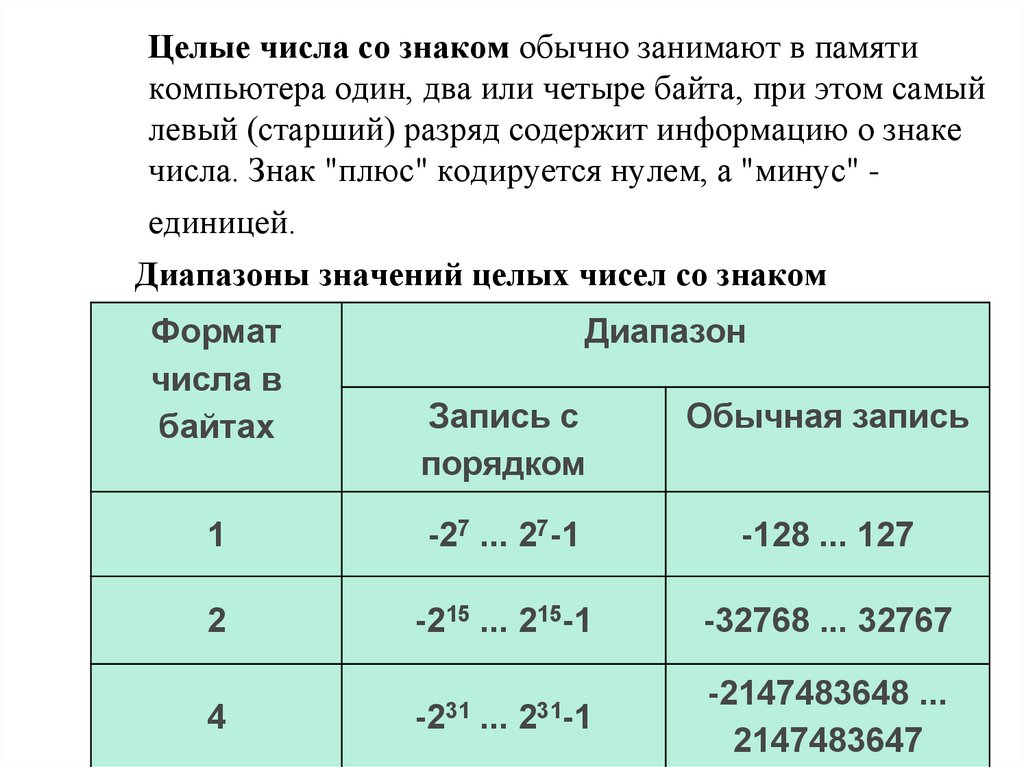
Целые числа со знаком обычно занимают в памятикомпьютера один, два или четыре байта, при этом самый
левый (старший) разряд содержит информацию о знаке
числа. Знак "плюс" кодируется нулем, а "минус" -
единицей.
Диапазоны значений целых чисел со знаком
Формат
числа в
байтах
Диапазон
Запись с
порядком
Обычная запись
1
-27 ... 27-1
-128 ... 127
2
-215 ... 215-1
-32768 ... 32767
4
-231 ... 231-1
-2147483648 ...
2147483647
29.
Рассмотрим особенности записи целых чисел со знаком напримере однобайтового формата, при котором для знака
отводится один разряд, а для цифр абсолютной величины семь разрядов.
В компьютерной технике применяются три формы записи
(кодирования) целых чисел со знаком: прямой код,
обратный код, дополнительный код.
Положительные числа в прямом, обратном и
дополнительном кодах изображаются одинаково двоичными кодами с цифрой 0 в знаковом разряде
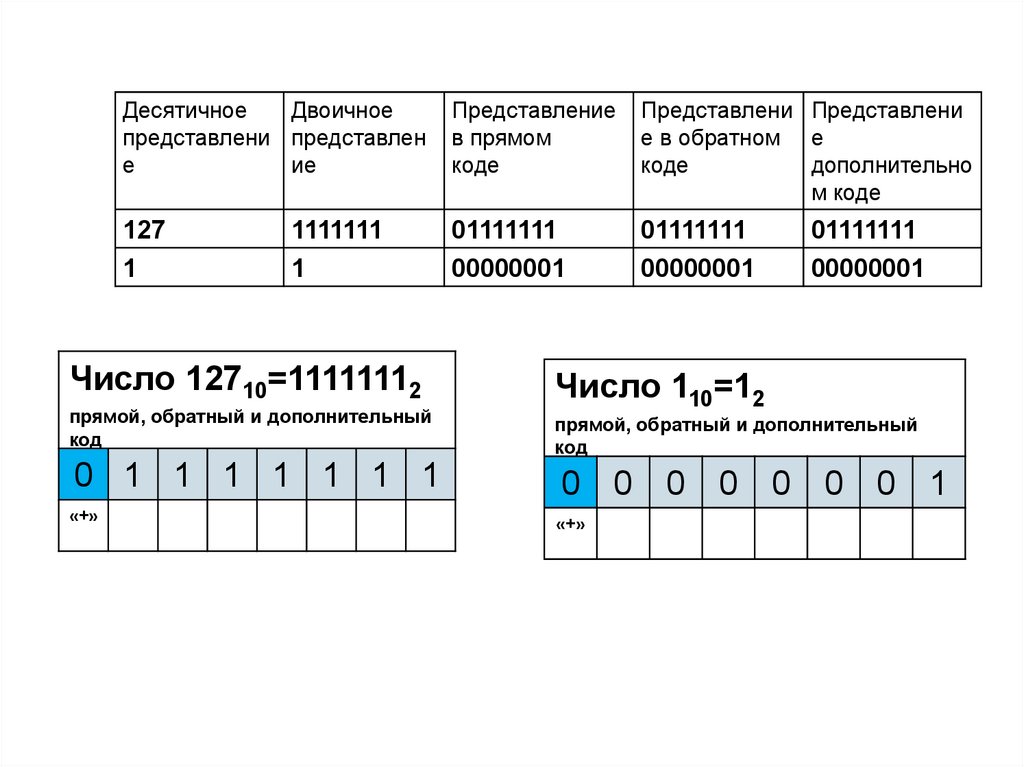
30.
ДесятичноеДвоичное
представлени представлен
е
ие
Представление
в прямом
коде
Представлени Представлени
е в обратном е
коде
дополнительно
м коде
127
1
01111111
00000001
01111111
00000001
1111111
1
Число 12710=11111112
прямой, обратный и дополнительный
код
01111111
00000001
Число 110=12
прямой, обратный и дополнительный
код
0 1 1 1 1 1 1 1
0 0 0 0 0 0 0 1
«+»
«+»
31.
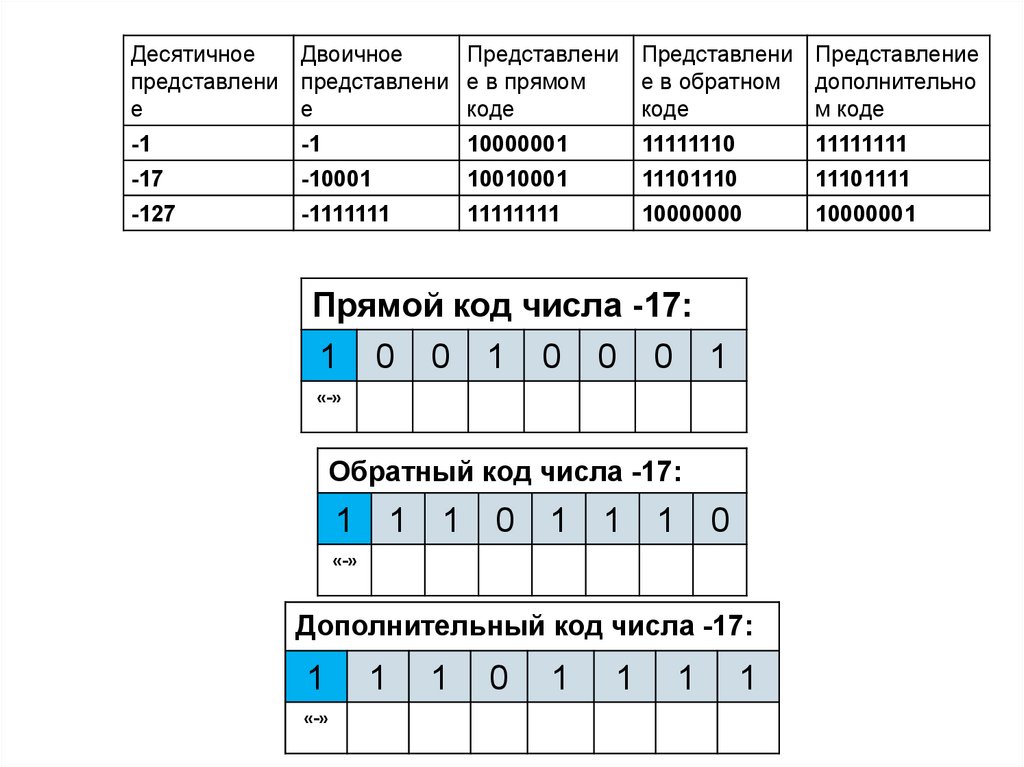
Отрицательные числа в прямом, обратном идополнительном кодах имеют разное изображение.
Прямой код. В знаковый разряд помещается цифра 1, а в
разряды цифровой части числа - двоичный код его
абсолютной величины
[-23]пк=1.0010111
Обратный код. Получается инвертированием всех цифр
двоичного кода абсолютной величины числа, включая
разряд знака: нули заменяются единицами, а единицы –
нулями.
[-23]ок=1.1101000
Дополнительный код. Получается образованием
обратного кода с последующим прибавлением единицы к
его младшему разряду.
[-23]дк=1.1101001
32.
ДесятичноеДвоичное
Представлени Представлени Представление
представлени представлени е в прямом
е в обратном дополнительно
е
е
коде
коде
м коде
-1
-1
10000001
11111110
11111111
-17
-10001
10010001
11101110
11101111
-127
-1111111
11111111
10000000
10000001
Прямой код числа -17:
1
0
0
1
0
0
0
1
«-»
Обратный код числа -17:
1
1
1
0
1
1
1
0
«-»
Дополнительный код числа -17:
1
«-»
1
1
0
1
1
1
1
33.
34.
35.
Операции над числами сфиксированной точкой
A-B=A+(K-B)-K
Kдоп=qn; Kобр=qn-1.
q=2, n=8
Kдоп=28=256=1000000002
Kобр=28-1=255=111111112
Кобр
1 1 1 1 1 1 1 1
[+3]
0 0 0 0 0 0 1 1
[-3]ок
1 1 1 1 1 1 0 0
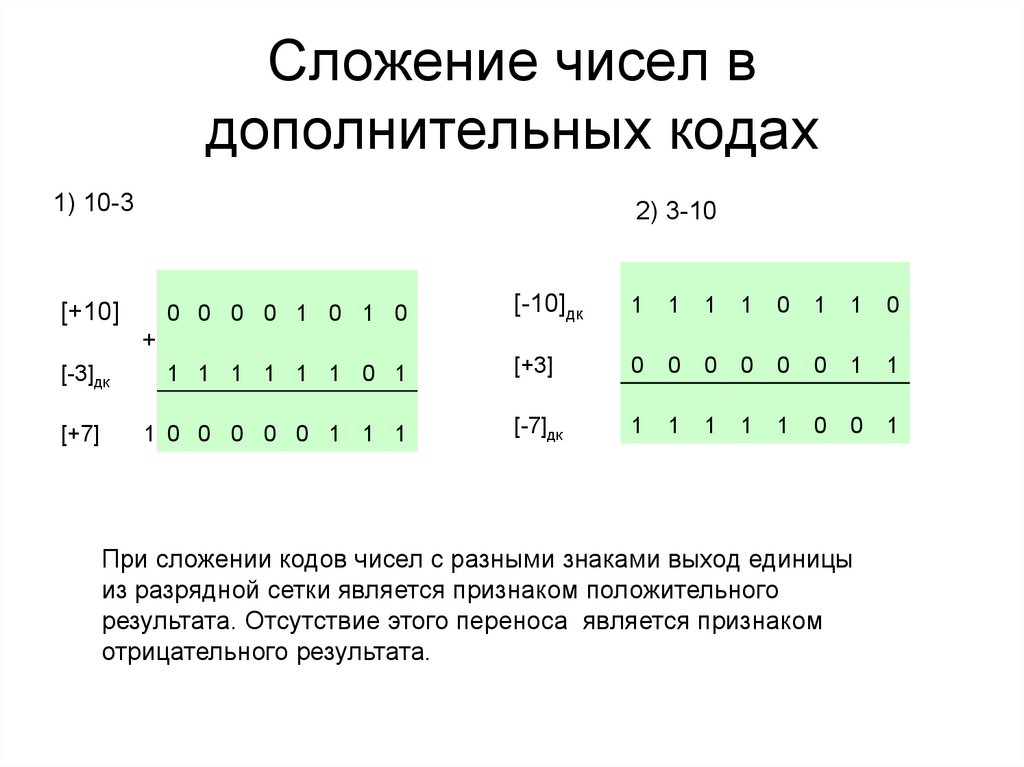
36. Сложение чисел в дополнительных кодах
1) 10-32) 3-10
0 0 0 0 1 0 1 0
[-10]дк
1
1
1
1
0
1
1
0
[-3]дк
1 1 1 1 1 1 0 1
[+3]
0
0
0
0
0
0
1
1
[+7]
1 0 0 0 0 0 1 1 1
[-7]дк
1
1
1
1
1
0
0
1
[+10]
+
При сложении кодов чисел с разными знаками выход единицы
из разрядной сетки является признаком положительного
результата. Отсутствие этого переноса является признаком
отрицательного результата.
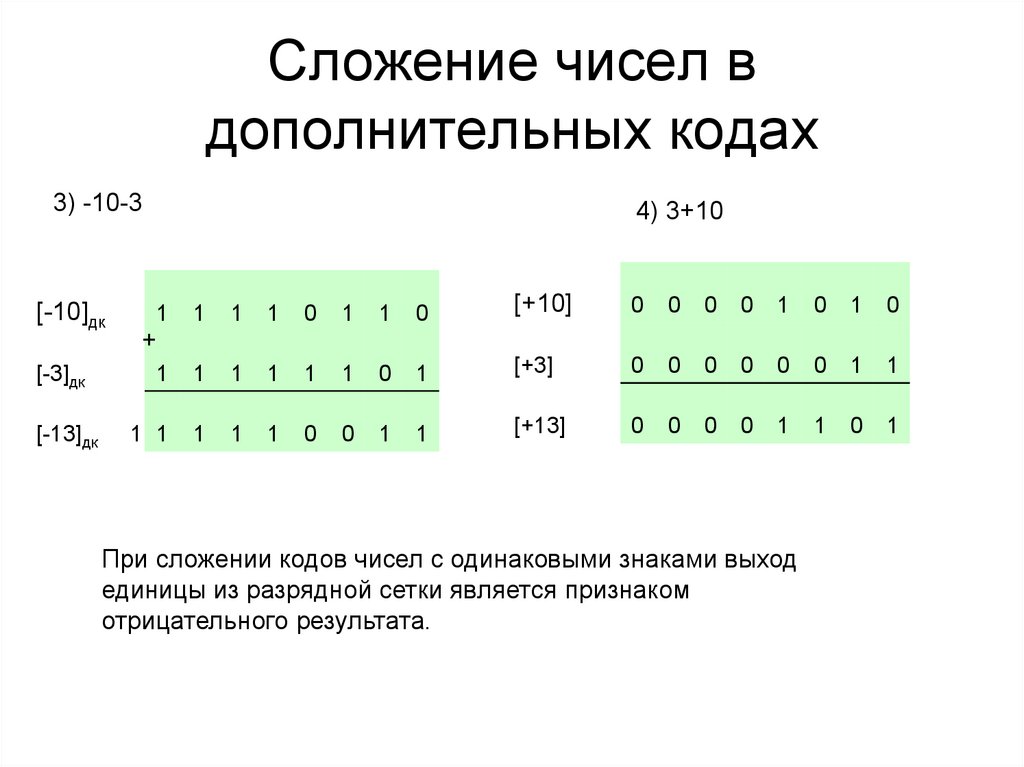
37. Сложение чисел в дополнительных кодах
3) -10-3[-10]дк
4) 3+10
1
1
1
1
0
1
1
0
[+10]
0
0
0
0
1
0
1
0
+
[-3]дк
1
1
1
1
1
1
0
1
[+3]
0
0
0
0
0
0
1
1
[-13]дк
1 1
1
1
1
0
0
1
1
[+13]
0
0
0
0
1
1
0
1
При сложении кодов чисел с одинаковыми знаками выход
единицы из разрядной сетки является признаком
отрицательного результата.
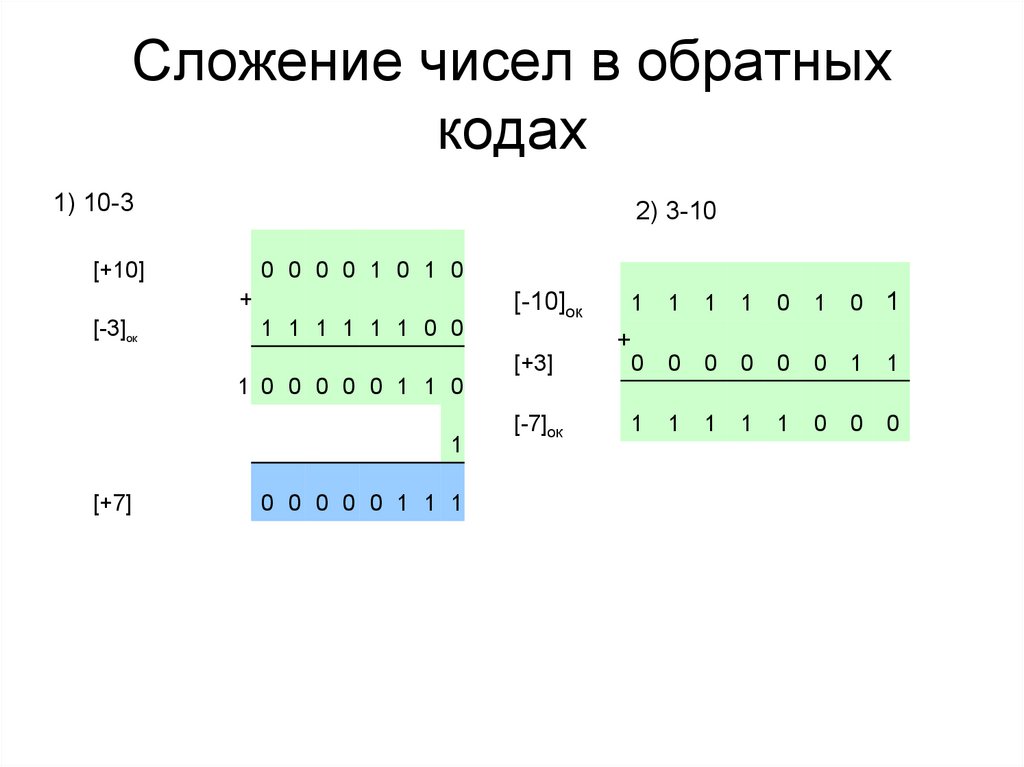
38. Сложение чисел в обратных кодах
1) 10-32) 3-10
[+10]
0 0 0 0 1 0 1 0
+
[-3]ок
1 1 1 1 1 1 0 0
1 0 0 0 0 0 1 1 0
1
[+7]
0 0 0 0 0 1 1 1
[-10]ок
[+3]
[-7]ок
1
1
1
1
0
1
0 1
0
0
0
0
0
0
1
1
1
1
1
1
1
0
0
0
+
39. Сложение чисел в обратных кодах
3) -10-3[-10]ок
1
[-3]ок
+1 1 1 1 1 1 0 0
1 1
1
1
1
1
1
1
0 1
0 0
0 1
0 1
1
[-13]ок
1
1
1
1
0 0
1 0
40.
Переполнение разрядной сетки[+65]
0 1 0 0 0 0 0 1
[+97]
0 1 1 0 0 0 0 1
1 0 1 0 0 0 1 0
Признаки переполнения разрядной сетки:
1.
Знак суммы не совпадает со знаками слагаемых;
2.
Переносы из старшего разряда суммы в знаковый и из
знакового не согласуются, т.е. один из них присутствует, а
другой отсутствует.
41.
Модифицированные коды00 – положительное число
11 – отрицательное число
01 – положительное переполнение
10 – отрицательное переполнение
[+65]
0 0 1 0 0 0 0 0 1
[+97]
0 0 1 1 0 0 0 0 1
0 1 0 1 0 0 0 1 0
42.
Представление вещественныхчисел
Любое вещественное число А может быть записано в
экспоненциальной форме:
±А =±m qp, где:
m - мантисса числа (множитель, содержащий все значащие
цифры числа);
q - основание системы счисления;
p - порядок числа.
Пример. 472 может быть представлено так:
4,72 102= 0,00472 105= 47200 10-2= 0,
0,472 103
Такое
представление
числа
называется
представлением в формате с плавающей запятой.
43.
Мантисса нормализованного числа должна быть правильнойдробью и иметь после запятой цифру, отличную от нуля.
1
Mq 1
q
(1)
Запись нуля считается нормализованной, если и мантисса, и
порядок равны нулю.
0,0000101012 0,101012 2 1002
44. Стандарт IEEE 754
Форматы чисел:Одинарный (single). Занимает в памяти 4 байта
32 разрядное нормализованное число со знаком, 8
разрядным смещенным порядком и 24 разрядной
мантиссой.
Двойной (double). Занимает в памяти 8 байтов
64 разрядное нормализованное число со знаком, 11
разрядным смещенным порядком и 53 разрядной
мантиссой.
45.
Формат с плавающей запятойs
e
m
Если k – это число разрядов, отводимое под порядок,
тогда
e p 2k 1 1
(2)
Для одинарного формата:
e p 28 1 1 p 127 p2 11111112
Для двойного формата:
e p 211 1 1 p 1023 p2 11111111112
46.
Формат с плавающей запятойs
e
m
Мантисса нормализованного числа в этих форматах
должна удовлетворять неравенству (3). Целая часть
мантиссы, всегда равная 1, не хранится в памяти (скрытая 1).
1 M2 2
(3)
Диапазон
представления
вещественных
чисел
определяется количеством разрядов, отведённых для
хранения порядка числа, а точность - количеством разрядов,
отведённых для хранения мантиссы.
47.
Пример представления числа в одинарном формате120,125=1111000,0012=1,111000001 2110
p=1102
e=1102+11111112=100001012
s=0 – число положительное
0
s
1
0
0
0
0
e
1
0
1
1
1
1
0
0
0
0
0
1
0 …
m
42F0400016 – внутреннее представление числа 120,125 в
одинарном формате
С2F0400016 – внутреннее представление числа -120,125 в
одинарном формате
48.
Пример представления числа в двойном форматеe=1102+11111111112=100000001012
s=1 – число отрицательное
1
s
1
0
0
0
0
0
e
0
0
1
0
1
1
1
1
0
0
0
0
0
1
0 …
m
С05Е08000000000016 – внутреннее представление числа -120,125
в двойном формате
49.
431BA00016 – внутреннее представление числа в одинарномформате
0
1
0
s
0
0
0
1
1
0
0
0
1
1
0
1
e
e
[-127]дк
1 0 0 0 0 1 1 0
+ 1 0 0 0 0 0 0 1
1 0 0 0 0 0 1 1 1
p=1112=7
1,00110111010 2111 = 10011011,1012=155,625
1
m
1
0
1 0
...
50.
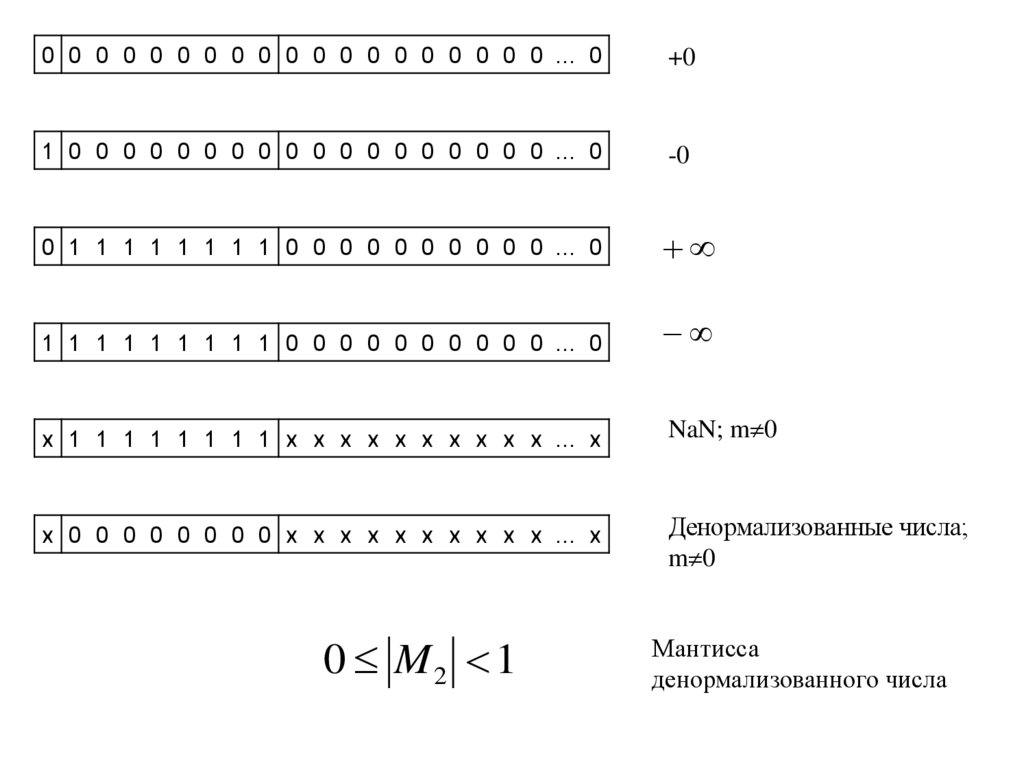
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 … 0+0
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 … 0
-0
0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 … 0
1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 … 0
x 1 1 1 1 1 1 1 1 x x x x x x x x x x … x
NaN; m 0
x 0 0 0 0 0 0 0 0 x x x x x x x x x x … x
Денормализованные числа;
m 0
0 M2 1
Мантисса
денормализованного числа
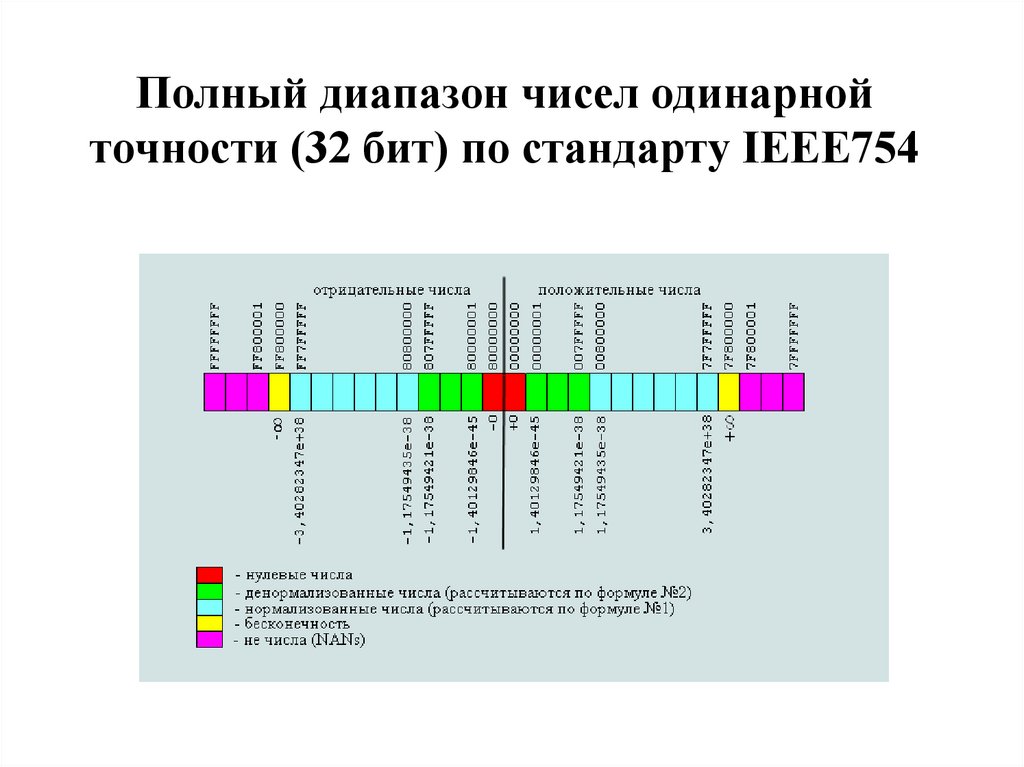
51. Полный диапазон чисел одинарной точности (32 бит) по стандарту IEEE754
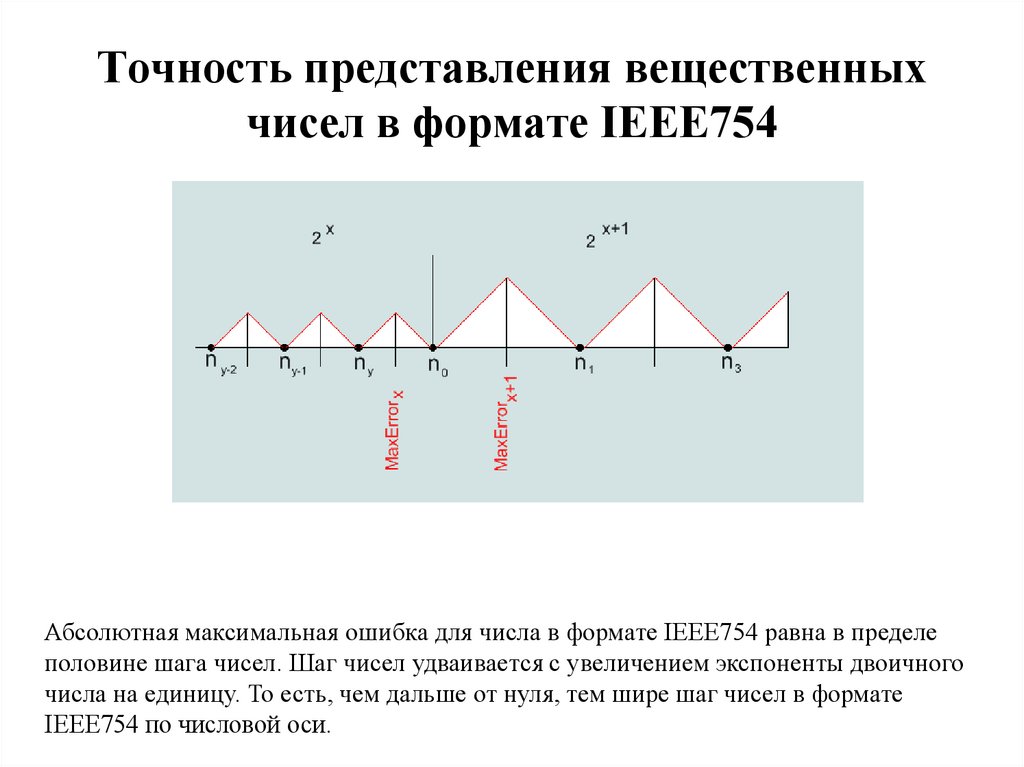
52. Точность представления вещественных чисел в формате IEEE754
Абсолютная максимальная ошибка для числа в формате IEEE754 равна в пределеполовине шага чисел. Шаг чисел удваивается с увеличением экспоненты двоичного
числа на единицу. То есть, чем дальше от нуля, тем шире шаг чисел в формате
IEEE754 по числовой оси.




































 informatics
informatics








