Реляционные языки (лекция 5)

1.

Федеральное государственное бюджетное
образовательное учреждение
высшего образования
«Оренбургский государственный университет»
Кафедра прикладной информатики в экономике и
управлении
БАЗЫ ДАННЫХ
1

2.

Тема : Реляционные языки
4 часа
Разработчик Панова Н.Ф.
2

3.

Реляционные языки
1 Введение в реляционные языки
2 Реляционная алгебра
3 Реляционное исчисление
3

4.

Реляционные
языки
используются
для
манипулирования данными, т.е. обеспечивают
выборку и обновление данных.
Реляционные языки делятся на две группы:
Процедурные;
Непроцедурные
4

5.

Процедурный язык можно описать как язык, с
помощью которого можно сообщить СУБД, как
построить новое отношение из одного или
нескольких
существующих
в
базе
данных
отношений.
5

6.

Непроцедурный реляционный язык определяет,
каким будет некоторое отношение, созданное на
основе одного или нескольких других отношений
базы данных.
6

7.

Реляционная алгебра — это высокоуровневый
теоретический процедурный
язык операций,
позволяющих создавать на основе одного или
нескольких отношений другое отношение без
изменения самих исходных отношений.
Операции реляционной алгебры делятся на 2
группы:
традиционные
операции над множествами
(объединение, разность, пересечение, декартово
произведение);
специальные реляционные операции (выборка,
проекция, деление, соединение).
7

8.

Некоторые операции могут выполняться
только над отношениями, совместимыми
по типу. Такие отношения должны иметь
одинаковые
схемы,
т.е.
одинаковое
количество атрибутов
с совпадающими
доменами;
Некоторые операции избыточны, т.е. могут
быть реализованы с помощью других
операций. Автор, Э.Кодд, выделил их как
самостоятельные операции, так как они
реализуют определенные виды запросов.
8

9.

Объединение
Объединением R ∪ S двух совместимых по типу
отношений R
и S называется отношение,
состоящее
из
множества
кортежей,
принадлежащих R или S или одновременно обоим
отношениям. Кортежи-дубликаты из результата
удаляются.
9

10.

Разность
Разностью R - S двух совместимых по типу
отношений
R
и
S
называется
отношение,
содержащие кортежи, которые принадлежат R и не
принадлежат S.
R-S
10

11.

Пересечение
Пересечением R∩S двух совместимых по типу
отношений R и S
называется отношение,
состоящие
из
множества
кортежей,
принадлежащих
одновременно
обоим
отношениям.
R∩S
11

12.

Избыточность операции пересечение
Пересечение можно реализовать с помощью
других операций
R∩S = R – (R – S)
12

13.

Декартово произведение
Операция декартова произведения R x S
определяет новое отношение, которое является
результатом
конкатенации
(т.е.
сцепления)
каждого кортежа из отношения R с каждым
кортежем из отношения S.
R
Поставщик
ООО «Нива»
Завод №1
S
Товар
Вафли
Батон
ЗАО «Колос»
13

14.

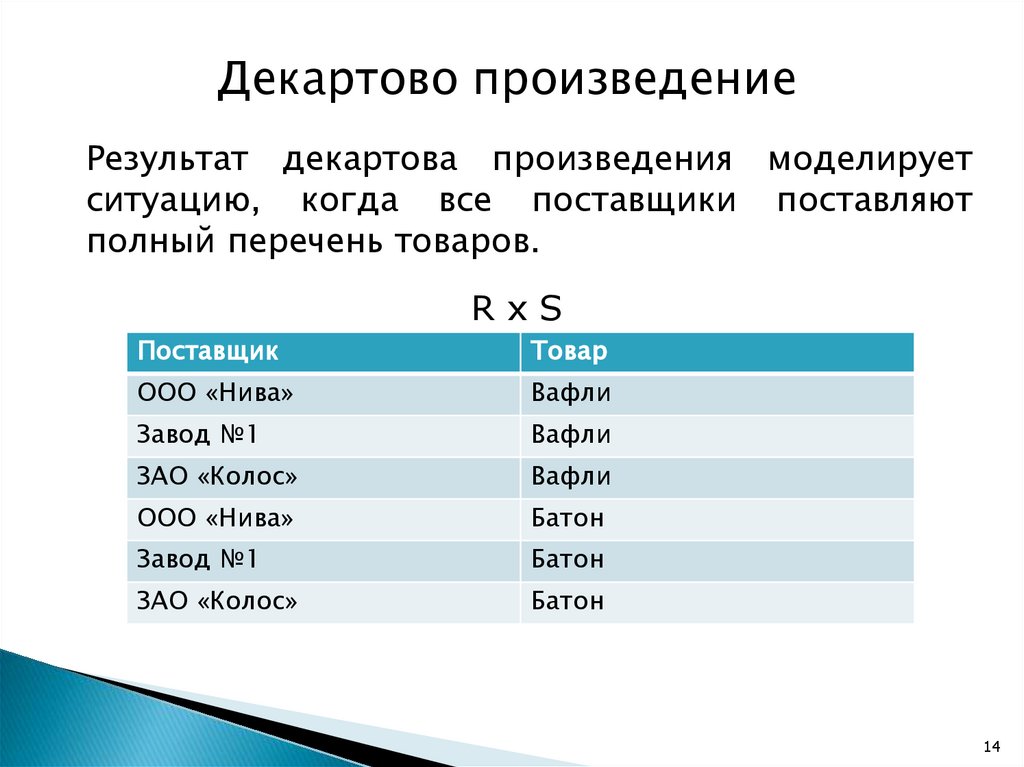
Декартово произведение
Результат декартова произведения моделирует
ситуацию, когда все поставщики поставляют
полный перечень товаров.
RxS
Поставщик
Товар
ООО «Нива»
Вафли
Завод №1
Вафли
ЗАО «Колос»
Вафли
ООО «Нива»
Батон
Завод №1
Батон
ЗАО «Колос»
Батон
14

15.

Проекция
Проекция П атр.1, …атр.n (R) – это унарная операция,
которая выполняется над одним отношением R и
возвращает
новое
отношение,
содержащее
вертикальное подмножество исходного отношения,
создаваемое путем извлечения значений указанных
атрибутов.
Кортежи-дубликаты
из
результата
исключаются.
15

16.

Выборка
Выборка F (R)– эта унарная операция , которая
выполняется над одним отношением и возвращает
горизонтальное
подмножество
исходного
отношения, содержащее множество кортежей
отношения
R,
удовлетворяющих
заданному
предикату (условию) F.
Цена >1000 (R)
Пример реализует запрос: выбрать сведения о
товарах, цена которых превышает 1000. Более
сложные предикаты содержат логические операции
AND, NOT, OR.
16

17.

Деление
Пусть отношение R определено на множестве
атрибутов А, а отношение S определено на
множестве атрибутов B, причём В ⊆ A , т.е. B
является подмножеством А.
Пусть С= А-В, т.е. С - это множество атрибутов
отношения R, которые не являются атрибутами
отношения S.
Тогда результатом деления R ÷ S является
отношение,
определённое
на
множестве
атрибутов С и содержащее набор кортежей
отношения
R,
которые
соответствуют
комбинации всех кортежей S.
17

18.

Деление
Пусть S содержит номенклатуру изделий,
которую выпускает завод. Пусть отношение R
содержит сведения о том, какие изделия в
цехах действительно выпускаются. Требуется
определить
номера
цехов,
в
которых
выпускается вся номенклатура изделий.
18

19.

Деление
Такой запрос реализуется с помощью операции
деления.
19

20.

Деление
Операция деления является избыточной, так как
её можно сформулировать на основе других
операторов:
Т1=Пс (R);
Т2= Пс ((SxT1)-R);
T=T1-T2
Для
рассмотренного
выше
примера
последовательность действий будет следующей:
множество С состоит из одного атрибута – цех.
Выполним операцию Пс(R). В результате получим
отношение Т1,содержащее номера всех цехов.
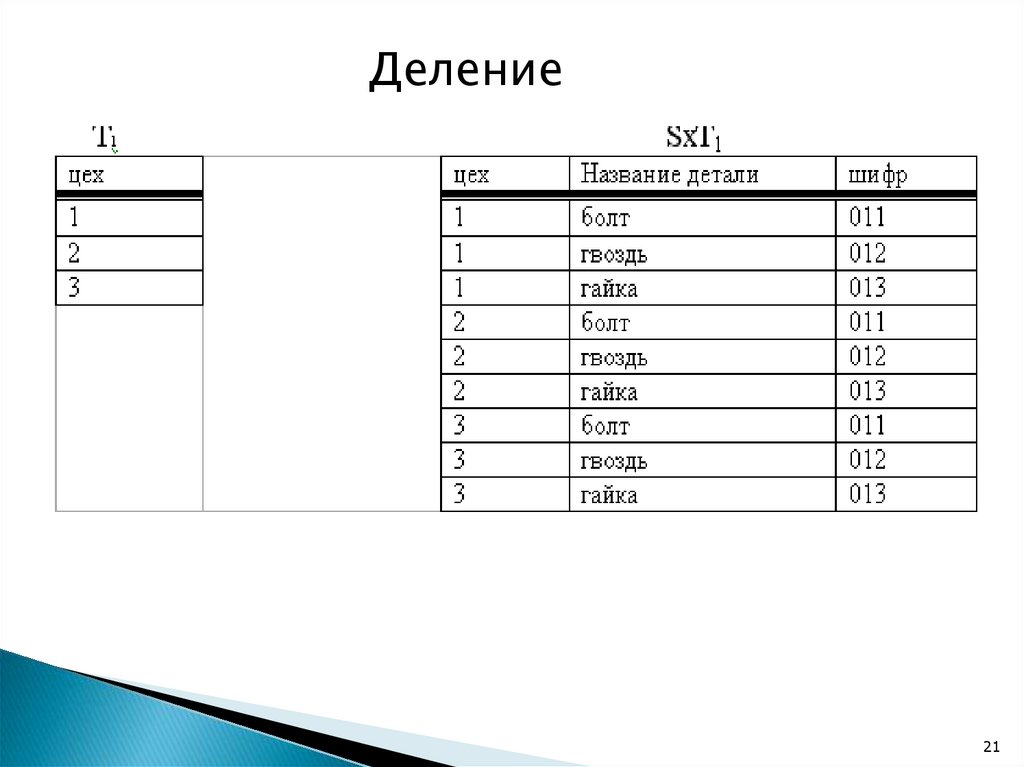
Результатом операции SxT1 будет отношение,
содержимое которого моделирует ситуацию, когда
все цеха выпускают полную номенклатуру изделий.
20

21.

Деление
21

22.

Деление
Выполнив операцию (SxT1)-R получим
отношение, содержащее список цехов и изделий,
которые на самом деле в данных цехах не
производятся.
22

23.

Деление
Результатом операции проекции
Т2= Пс ((SxT1)-R) будет множество цехов, в
которых полная номенклатура изделий не
выпускается.
Если исключить это множество из множества
всех цехов, т.е. выполнить операцию T1-T2,
результат запроса будет получен.
23

24.

Соединение
Операция соединения выполняется над
двумя отношениями.
Существует несколько типов операций
соединения.
тета- соединение (θ - Join);
соединение по эквивалентности;
внешнее
или
открытое
(outer
join)
соединение;
24

25.

Тета - соединение
Тета-соединение
R⋈FS
возвращает
отношение,
которое
содержит
кортежи
декартового произведения отношений R и S,
удовлетворяющие предикату F.
Предикат F имеет вид R.ai θ S.bi ,
где ai – атрибут R,
bi – атрибут S,
операция
θ
означает
операцию
отношения < , > , = , >= , <= или <>.
25

26.

Тета - соединение
Обозначение
тета-соединения
можно
переписать на основе базовых операций
выборки и декартова произведения, как
показано ниже.
R⋈FS = F( R x S)
26

27.

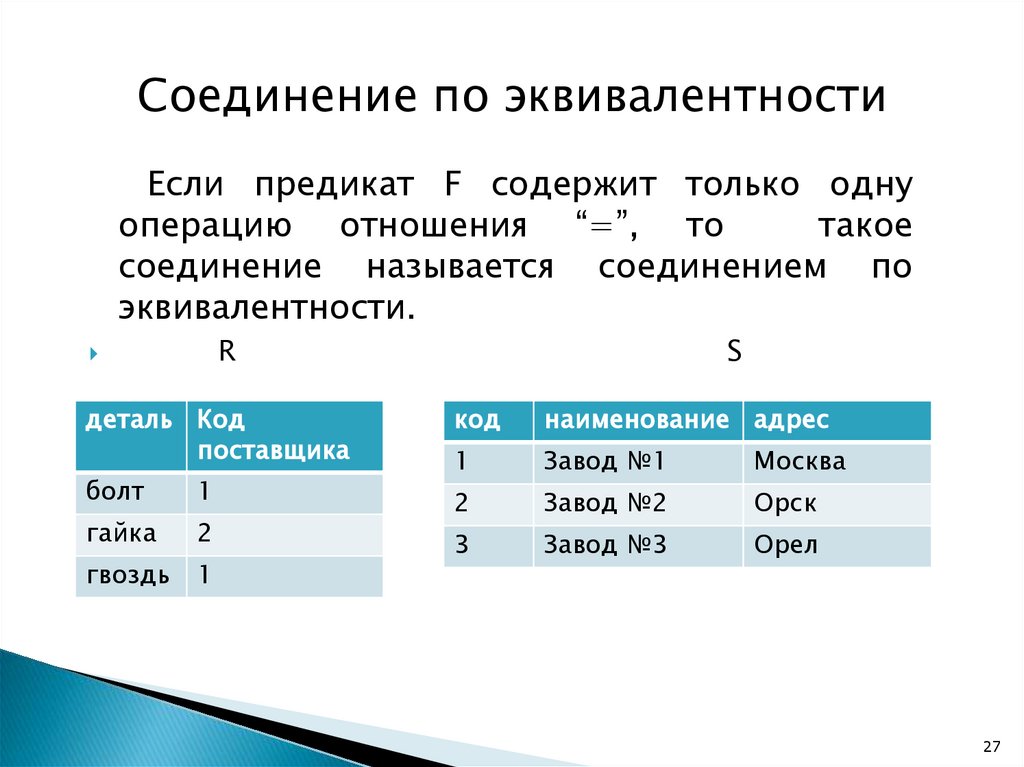
Соединение по эквивалентности
Если предикат F содержит только одну
операцию отношения “=”, то
такое
соединение называется соединением по
эквивалентности.
R
S
деталь Код
поставщика
код
наименование адрес
болт
1
1
Завод №1
Москва
гайка
2
2
Завод №2
Орск
гвоздь
1
3
Завод №3
Орел
27

28.

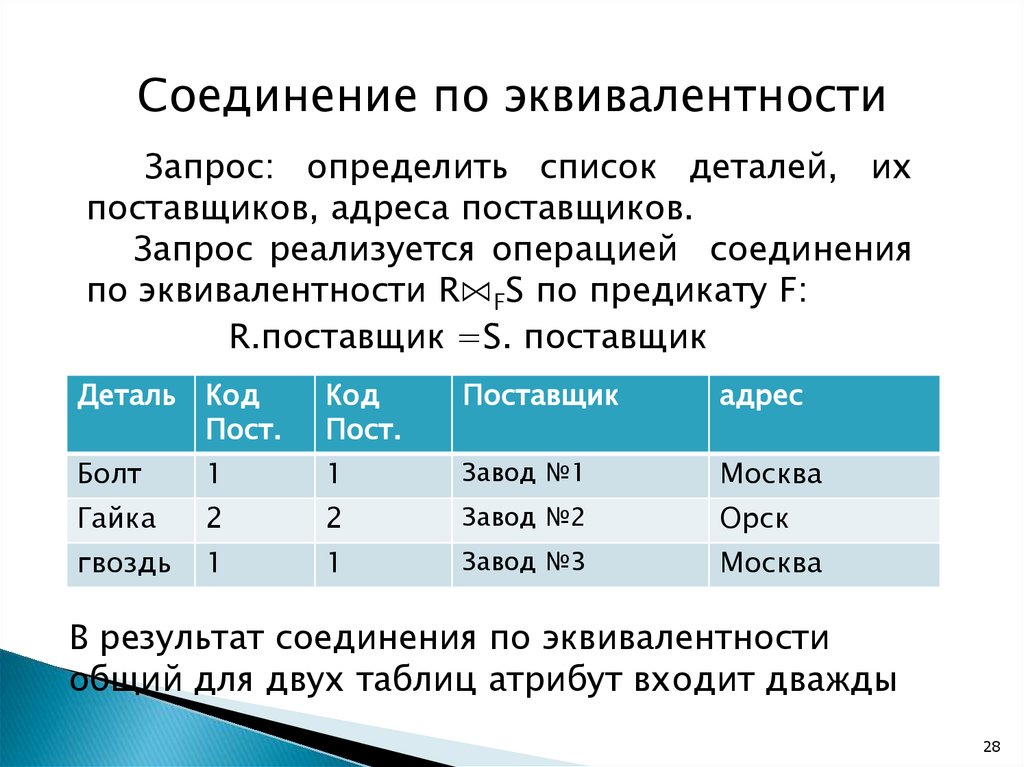
Соединение по эквивалентности
Запрос: определить список деталей, их
поставщиков, адреса поставщиков.
Запрос реализуется операцией соединения
по эквивалентности R⋈FS по предикату F:
R.поставщик =S. поставщик
Деталь
Код
Пост.
Код
Пост.
Поставщик
адрес
Болт
1
1
Завод №1
Москва
Гайка
2
2
Завод №2
Орск
гвоздь
1
1
Завод №3
Москва
В результат соединения по эквивалентности
общий для двух таблиц атрибут входит дважды
28

29.

Естественное соединение
R ⋈ S. Естественным соединением называется
соединение
по
эквивалентности
двух
отношений R и S, выполненное по всем общим
атрибутам,
из
результатов
которого
исключается по одному экземпляру каждого
общего атрибута.
R⋈S
Деталь
Код
Пост.
наименов адрес
ание
Болт
1
з-д 1
Москва
Гайка
2
з-д 2
Орск
гвоздь
1
з-д 1
Москва
29

30.

Внешние соединения
Внешние соединения используются, когда
требуется,
чтобы
кортеж
одного
из
отношений
вошел
в
результирующее
отношение, даже если в другом отношении
для него не нашлось совпадающего
значения.
30

31.

Внешние соединения
Внешние соединения бывают следующих
видов:
левое внешнее соединение;
правое внешнее соединение;
полное внешнее соединение.
31

32.

Левое внешнее соединение
R ⊳ S. Левым внешним соединением
называется соединение, при котором в
результирующее
отношение
включаются
также кортежи отношения R, не имеющие
совпадающих значений в общих столбцах
отношения S.
Для обозначения отсутствующих значений
во втором отношении используется значение
null.
32

33.

Левое внешнее соединение. Пример
:
Отношение абитуриент
содержит перечень
абитуриентов,
в
отношении
Результаты
тестирования хранятся даты и количество
баллов,
набранных
абитуриентами
при
прохождении тестирования. Однако не все
абитуриенты успели пройти тесты.
33

34.

Левое внешнее соединение. Пример
Требуется вывести список абитуриентов с
результатами тестирования, включая тех, кто ещё
не успел его пройти.
Такой запрос может быть реализован с
помощью левого внешнего соединения.
Абитуриент ⊃⊳ Результаты тестирования
Код
Фио
Специальность
Дата
результат
117
Иванов
ПИ
21.08.19
120
503
Сидоров
ИН
25.08.19
75
224
Петров
ИСТ
Null
Null
34

35.

Правое внешнее соединение
R ⊲⊂ S. Правым внешним соединением
называется
соединение,
при
котором
кортежи S, не имеющие совпадений в общих
столбцах отношения R, также включаются в
результирующее отношение.
Отсутствие совпадающих значений во
втором отношении задаётся определителем
null.
Рассмотренный выше запрос может быть
реализован и с помощью операции правого
внешнего соединения
Результаты тестирования ⊲⊂ Абитуриент
35

36.

Полное внешнее соединение
R S . Полное внешнее возвращает
отношение, которое включает все кортежи из
обоих отношений и в котором для обозначения
несовпадающих
значений
используется
определитель null.
36

37.

Реляционное
исчисление
–
это
высокоуровневый теоретический непроцедурный
язык.
Различают реляционное исчисление кортежей и
реляционное исчисление доменов.
37

38.

Термин исчисление заимствован из раздела
логики,
который
называется
исчислением
предикатов. Под предикатом
понимается
истинностная функция с аргументами.
Если P – предикат, то множество всех значений
переменной, для которых значение Р становится
истинным, можно записать следующим образом:
{x │ P(x)}.
38

39.

В реляционном исчислении кортежей задача
состоит в нахождении таких кортежей, для
которых предикат становится истинным. Это
исчисление основано на переменных кортежа.
Переменными
кортежа
являются
такие
переменные, областью определения которых
служит указанное отношение.
В реляционном исчислении доменов также
используются переменные, но их значения
берутся из области определения атрибутов, а не
из кортежей отношения.
39

40.

Любому выражению реляционного исчисления
можно сопоставить операцию реляционной
алгебры и наоборот.
Пример:
Пусть R1= {r1}, т.е. отношение R1состоит из
множества кортежей {r1},
R2= {r2}, т.е. отношение R2 состоит из
множества кортежей {r2}.
Тогда выражение
{r | r є R1 ∨r є R2} описывает отношение,
которое является объединением отношений R1
и R2, т. е. это выражение эквивалентно
операции реляционной алгебры R1 ∪ R2.
40

41.

Пусть R1= {r1}, т.е. отношение R1состоит из
множества кортежей {r1},
R2= {r2}, т.е. отношение R2 состоит из
множества кортежей {r2}.
Тогда выражение
{r | r є R1 ∧r є R2} эквивалентно операции
реляционной алгебры R ∩ S.
{r | r є R1 ∧r R2} эквивалентно операции
реляционной алгебры R - S.
Студент(код, фио, группа)
R=Пфио(Студент) эквивалентно выражению
{r.фио | r є Студент}
41

42.

1. На какие группы делятся реляционные языки?
2. Что используют операции реляционных языков
в качестве операндов?
3. На какие группы делятся операции
реляционной алгебры?
4. Какие операции реляционной алгебры требуют
совместимости по типу исходных отношений?
5. Назовите специальные реляционные операции.
6. Какие операции реляционной алгебры являются
унарными?
7. Какие типы переменных используются в
выражениях реляционного исчисления?
42

43.

1. Клиент(код, ФИО, дата рождения)
2. Агент( код, ФИО, должность)
3. Тип договора (код, наименование)
4. Договор(номер, дата, сумма, код_агента,
код_клиента, код_типа_договора)
5. Запросы
6. Получить список наименований должностей
агентов
7. R = П наименование (Должность)
8. Получить сведения о клиентах старше 60 лет
9. R = F (Клиент)
10.F: дата рождения <’01.01.1956’
43

44.

Получить даты, на которые заключены
договора на суммы от 500 до 1000 рублей
R = F (Договор)
F: сумма>=500 сумма<=1000
R1 = П дата (R)
44

45.

Получить даты, в которые были заключены договора
между агентом Ивановым и клиентом Петровым
R1 = договор ⋈F агент
F: Договор. Код_агента = Агент.код
R2 = R1 ⋈F Клиент
F: R1.код_клиента = Клиент.код
1. R3 = F (R1)
2. F: ФИО_агента=«Иванов» ФИО_клиента=«Петров»
3. R4 = П дата (R3)
45

46.

1. Выяснить ФИО агентов, которые в сентябре 2020 года
не заключили ни одного договора
R1 = F (Договор)
F: дата>=’01.09.20’ дата<=‘30.09.20’
R2 = R1 ⋈F агент
F: R1. Код_агента = Агент.код
R4 = П ФИО (R2) – ФИО агентов, которые в сентябре
договора заключали
R5 = П ФИО (агент) – ФИО всех агентов
R6 = R5-R4
46