Коллоидная химия. Молекулярно - кинетические свойства дисперсных систем (лекция 4)

1. Коллоидная химия ИТХТ им. М.В. Ломоносова кафедра НС и ПЯ группы ХХБО-01-03-2022

ЛЕКЦИЯ 4
Шубенкова Екатерина Гаррьевна

2. Коллоидная химия

ЛЕКЦИЯ 4
Молекулярно-кинетические
свойства дисперсных систем
Шубенкова Е.Г.
2024

3. План лекции:

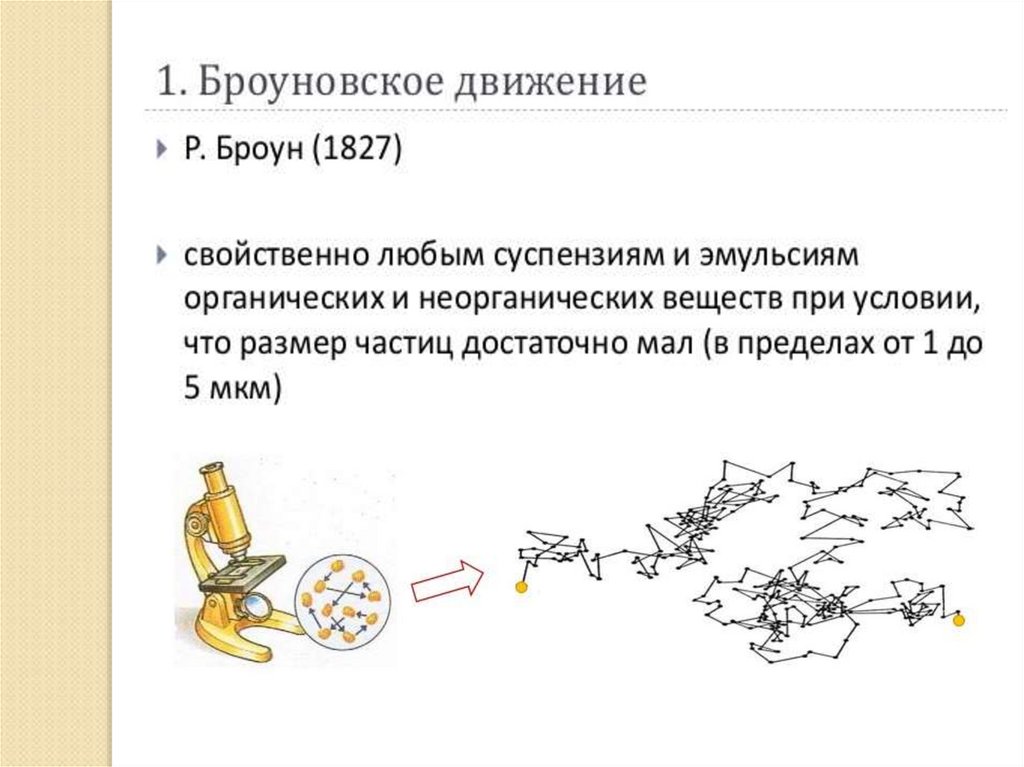
1. Броуновское движение, его причины и общенаучное
значение.
2. Понятие о диффузии. Первый и второй законы Фика.
3. Физический смысл коэффициента диффузии, его
размерность. Уравнение Эйнштейна-Стокса.
4. Соотношение между среднеквадратичным сдвигом и
коэффициентом диффузии. Вывод уравнения Эйнштейна Смолуховского.
5. Седиментация прямая и обратная, поток седиментации.
6. Седиментационное уравнение незаряженной частицы.
Диффузионно-седиментационное равновесие. Вывод
гипсометрического закона.
7. Дисперсный анализ. Уравнение для определения
радиуса частиц дисперсной фазы по скорости
седиментации. Интегральные и дифференциальные
кривые распределения частиц полидисперсных систем по
размерам.
8. Седиментация в центробежном поле. Определение
массы частицметодами скоростного и равновесного
ультрацентрифугирования.

4.

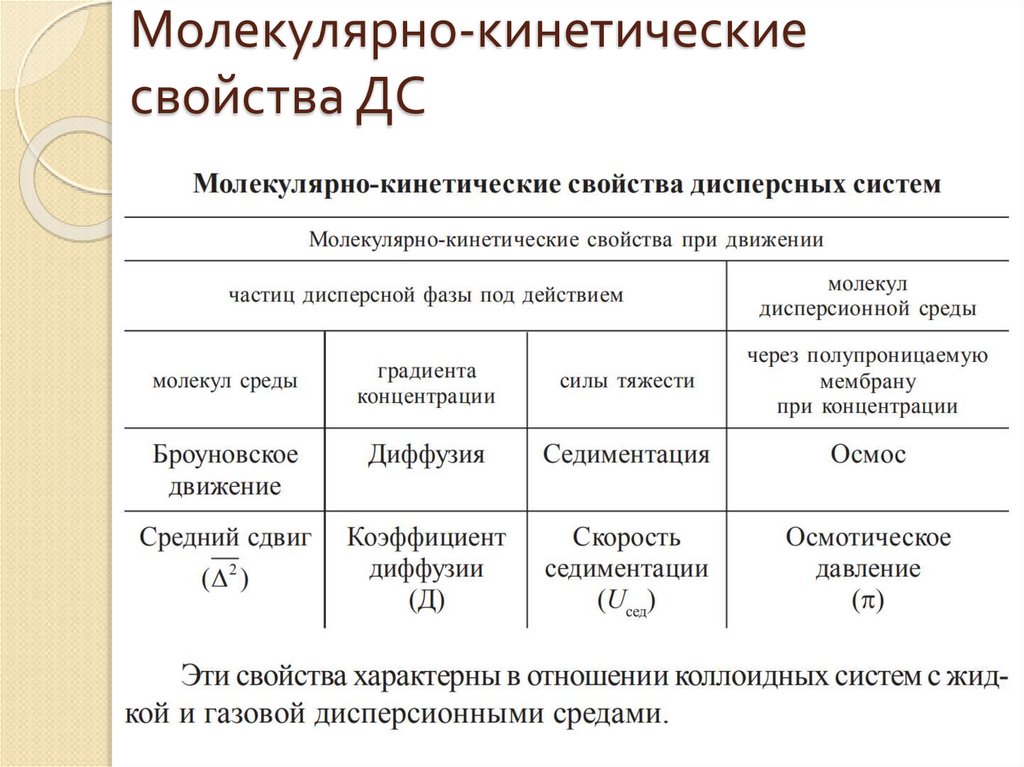
5. Молекулярно-кинетические свойства коллоидных растворов

6. Молекулярно-кинетические свойства ДС

7.

8.

9.

10. Общенаучное значение броуновского движения

Общенаучное
движения
значение
броуновского
1. Теоретическое обоснование тепловой природы броуновского
движения
явилось
доказательством
реальности
существования молекул. В связи с этим теория броуновского
движения
убедительно
склонила
чашу
весов
в
пользу
материалистического мировоззрения.
2.
С
помощью
броуновского
движения
доказывается
статистический характер второго закона термодинамики.
В результате броуновского движения возникают флуктуации
концентрации на молекулярном уровне или уровне малых частиц.
Когда коллоидная частица самопроизвольно поднимается в
броуновском движении, потенциальная энергия системы возрастает.
При опускании частицы вниз за счет возросшей потенциальной
энергии можно совершить работу. Следовательно, теплота
окружающей среды превращается в работу в отсутствие начальной
разности температур, то есть мы приходим к неверному выводу о
том, что действует вечный двигатель второго рода.
Ошибочность подобного заключения состоит в том, что подобная
схема применима к отдельной частице, но не применима к
множеству частиц.
Согласно теории вероятностей, при большом числе частиц, если
одна
частица
движется
вверх,
приводя
к
увеличению
потенциальной энергии, то всегда найдется другая частица,
двигающаяся вниз, и потенциальная энергия не изменится.
Таким
образом,
второе
начало
термодинамики
не
применимо к отдельной частице, так как оно является
вероятностным законом. Так броуновское движение привело
к доказательству статистического характера второго закона
термодинамики.

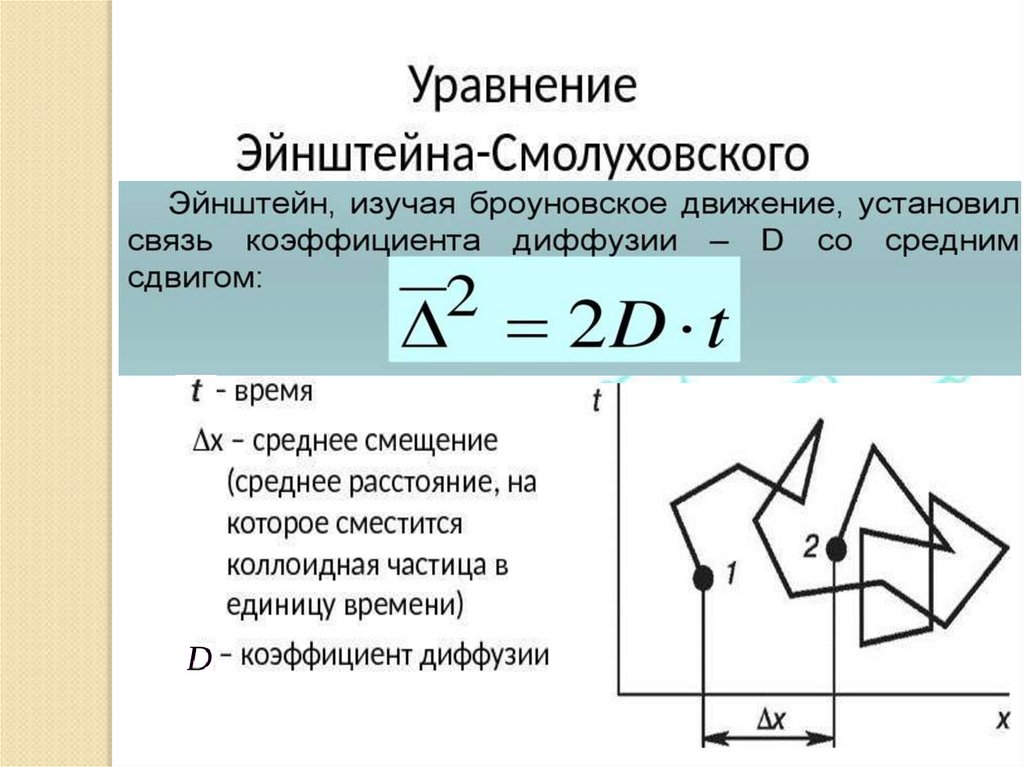
11. Средний сдвиг частицы

Эйнштейн создал в 1905 году статистическую теорию
броуновского движения.
Основным постулатом этой теории является полная
хаотичность движения, то есть рассмотрение движения
частицы как «случайного блуждания» в трех измерениях в
нем наблюдается совершенная равноправность всех
направлений.
Истинный
путь
движения
частицы
определить невозможно, но можно определить среднее
расстояние, на которое она смещается.
Для количественных расчетов
применяют среднеквадратичное
значение проекции смещения
частицы:
21 22 ...
n
Проекция траектории движения
частицы на плоскость.
где n - число отдельных проекций.
Среднеарифметическое
значение
проекции смещения равно нулю, так
как
все
направления
движения
равновероятны.

12.

13.

14.

15.

Первый закон Фика характеризует стационарный процесс диффузии:

16.

КОЭФФИЦИЕНТ ДИФФУЗИИ

17.

ПРИМЕНЕНИЕ УРАВНЕНИЯ ЭНШТЕЙНА

18.

19. Вывод уравнения Эйнштейна–Смолуховского

Согласно Эйнштейну и Смолуховскому, поток диффузии при
переносе вещества вдоль направления х, составляет
1
1
c1 c2
2
Jd 2
c1 c2
2
Градиент концентрации, согласно этой модели, равен:
По первому закону Фика:
Jd D
При сравнении этих уравнений:
Jd
dc i
dx
dc
c c2
1
dx
c1 c2 D c 2 c1
2
получаем уравнение Эйнштейна – Смолуховского, которое
устанавливает взаимосвязь между макроскопическим и
микроскопическим описанием процесса диффузии:
2
2 D

20.

21. Второй закон Фика

Характеризует нестационарный процесс диффузии и
описывает накопление вещества в различных точках
пространства в зависимости от времени поглощения
вещества твердым телом, то есть сорбцию:
2
C
C
D
x 2
(4)
Зависимость коэффициента диффузии от температуры
выражается уравнением типа уравнения Аррениуса:
D DO e
ED RT
где ED - энергия активации диффузии.
(5)

22.

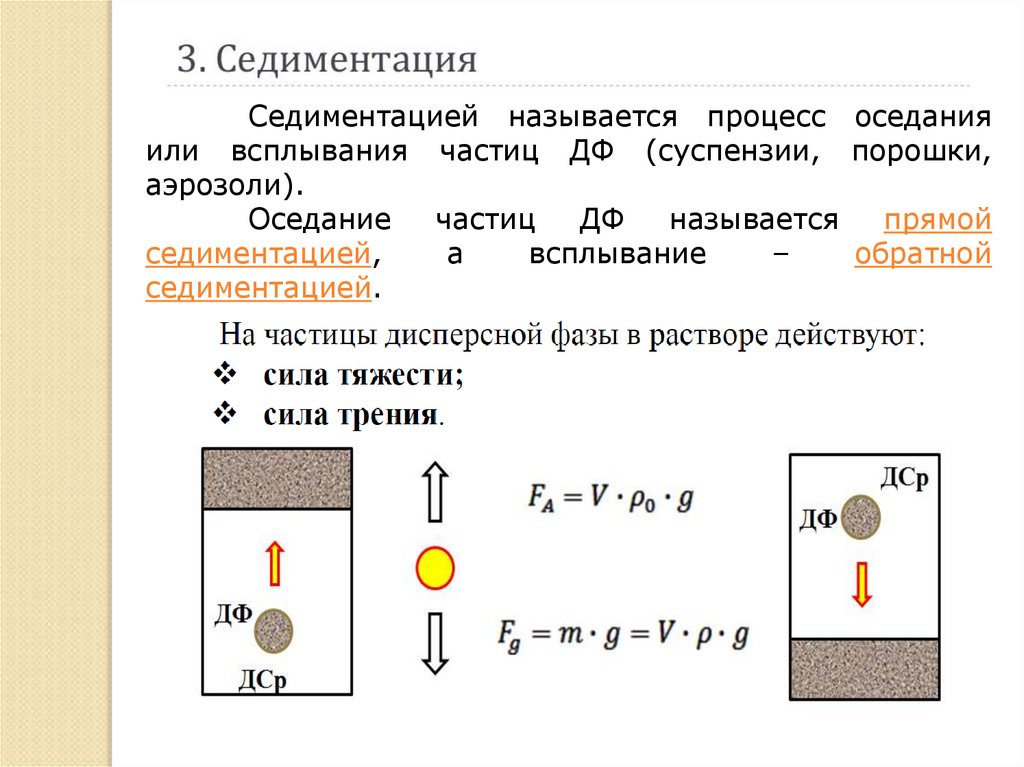
Седиментацией называется процесс оседания
или всплывания частиц ДФ (суспензии, порошки,
аэрозоли).
Оседание
частиц
ДФ
называется
прямой
седиментацией,
а
всплывание
–
обратной
седиментацией.

23.

24. УСЛОВИЯ ПРИМЕНЕНИЯ ЗАКОНА СТОКСА

1. Скорость оседания частицы должна быть
постоянной (применимо для частиц размером от 0,1 до
100 мкм).
2. Частицы должны иметь сферическую форму.
3. Оседающие частицы должны быть твердыми. При
анализе эмульсий в уравнение Стокса должны быть
введены поправки.
4. Частицы должны полностью смачиваться
жидкостью, в которой они оседают. В этом случае на
поверхности твердых частиц образуется слой из
молекул жидкости, перемещающийся вместе с
частицей. При движении происходит скольжение
между двумя слоями жидкости и в уравнении Стокса
величина действительно представляет собой
коэффициент вязкости жидкости.
5.На оседание отдельной частицы не должны влиять
соседние частицы (концентрация суспензий не выше
0,5-1%).
6. Скорость оседания частиц не должна превышать
определенного предела, иначе вблизи частицы
возникает турбулентное движение жидкости и
зависимость, выражаемая уравнением Стокса, не
соблюдается.

25.

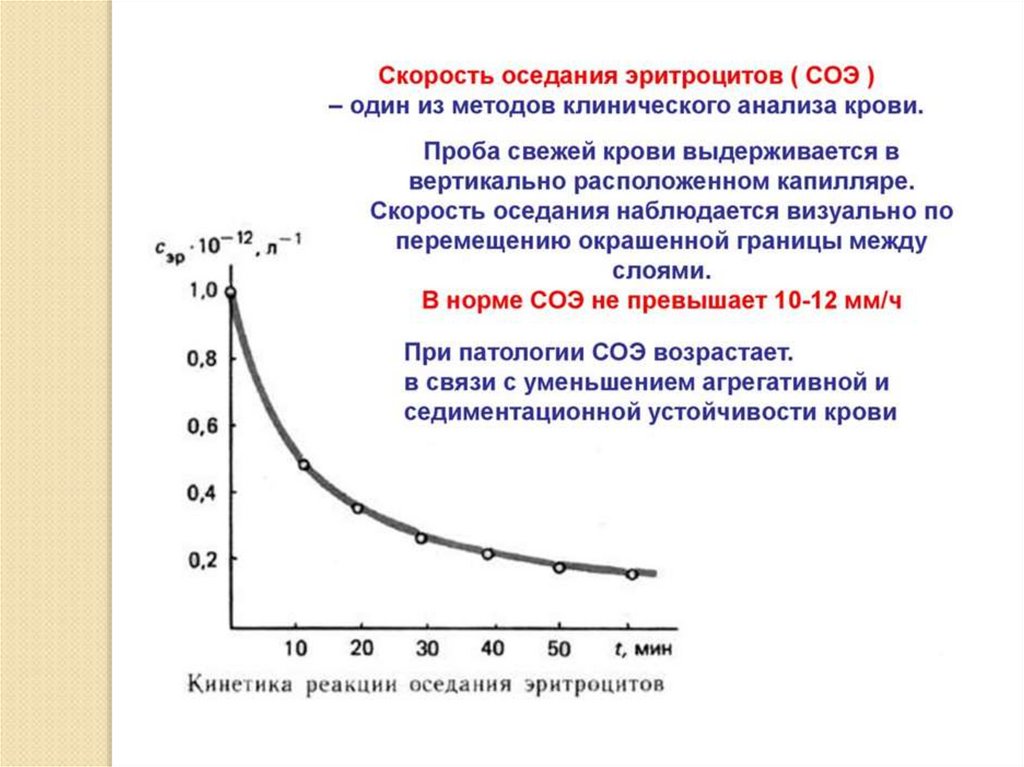
СКОРОСТЬ СЕДИМЕНТАЦИИ
Вначале частица движется ускоренно, так как сила тяжести
превышает силу трения. Однако по мере увеличения скорости
движения растет и сила трения, и в некоторый момент времени
сила трения уравновешивает силу тяжести, вследствие чего
частица начинает двигаться с постоянной скоростью.
H

26.

27.

28.

Кинетическая устойчивость обеспечивается
гидродинамическими факторами: вязкостью и
плотностью среды, плотностью и размером частиц.

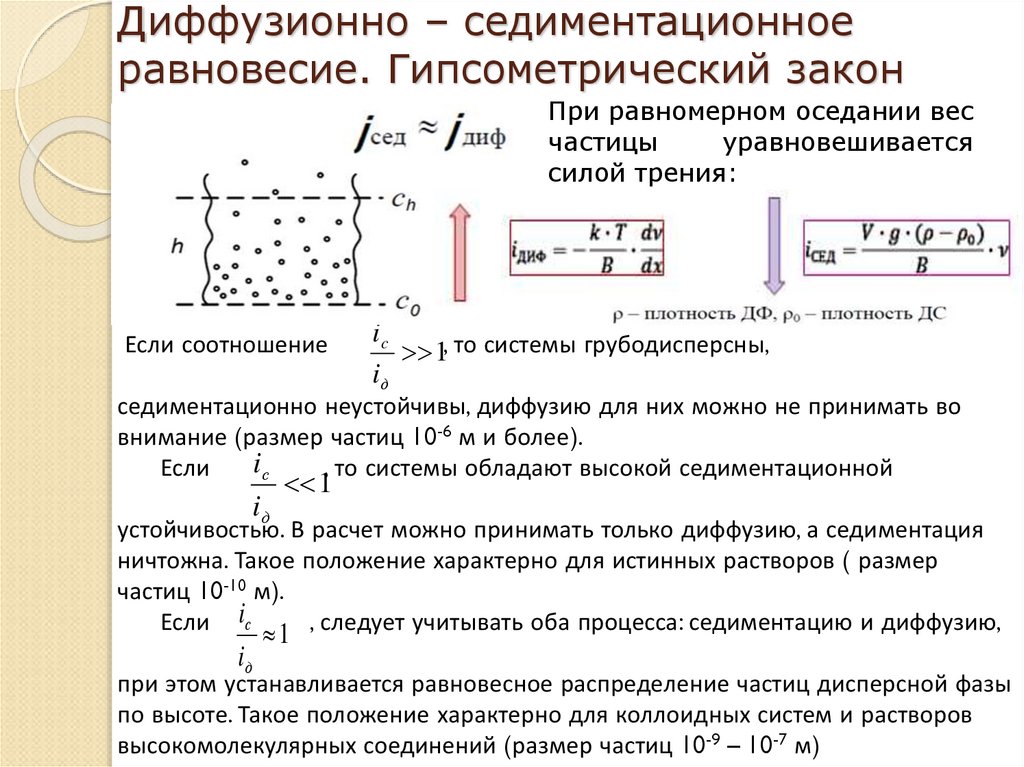
29. Диффузионно – седиментационное равновесие. Гипсометрический закон

При равномерном оседании вес
частицы
уравновешивается
силой трения:
Если соотношение
ic
1, то системы грубодисперсны,
iд
седиментационно неустойчивы, диффузию для них можно не принимать во
внимание (размер частиц 10-6 м и более).
iс
Если
, то системы обладают высокой седиментационной
iд
1
устойчивостью. В расчет можно принимать только диффузию, а седиментация
ничтожна. Такое положение характерно для истинных растворов ( размер
частиц 10-10 м).
Если iс
, следует учитывать оба процесса: седиментацию и диффузию,
iд
1
при этом устанавливается равновесное распределение частиц дисперсной фазы
по высоте. Такое положение характерно для коллоидных систем и растворов
высокомолекулярных соединений (размер частиц 10-9 – 10-7 м)

30.

При условии равновесия
:
.
m g
dс
с D
B
dx
iс iд
k T
B
dс m g
dx
с
k T
D
m g
k T dс
с
B
B dx
Так как градиент концентрации изменяется по высоте, то
dx dh
После интегрирования получим:
c
m g h
ln 0
ch
k T
m g h
c0
e k T
ch
c h cO e
m g h
k T
Это частный случай распределения молекул по Больцману.
Если значение С заменить пропорциональным ей значением р, то
получим
p
m g h
ln O
ph
k T
или
pO
k T ln
m g h
ph
Это выражение известно под названием гипсометрического
закона,
определяющего распределение молекул газа по
высоте (hypsos-высота (лат)). Левая часть уравнения представляет собой
работу обратимого изотермического расширения моля газа, правая часть уравнения
является работой поднятия моля газа на высоту h.
Гипсометрический закон для золей записывается
в следующем виде:
k T ln
сO
1 V m g h
сh

31. Седиментационное уравнение незаряженной частицы

Рассмотрим седиментацию незаряженной частицы, масса
которой равна m, а объем - V , в жидкости плотностью ρ .
На частицу действуют направленные в разные стороны сила
тяжести m g и сила Архимеда m0 g ,
где - m0 масса
жидкости в объеме частицы, равная V .
Седиментационная сила, которая не зависит от
формы частицы, равна их разности:
__
f с m g V g m 1 V g
__
__
V - удельный объем частицы.
При оседании частицы действует сила трения, равная
BU
В – коэффициент трения
U – скорость седиментации
При стационарном режиме оседания седиментационная сила
уравновешивается силой трения.
__
m 1 V g B U

32. Седиментационный анализ

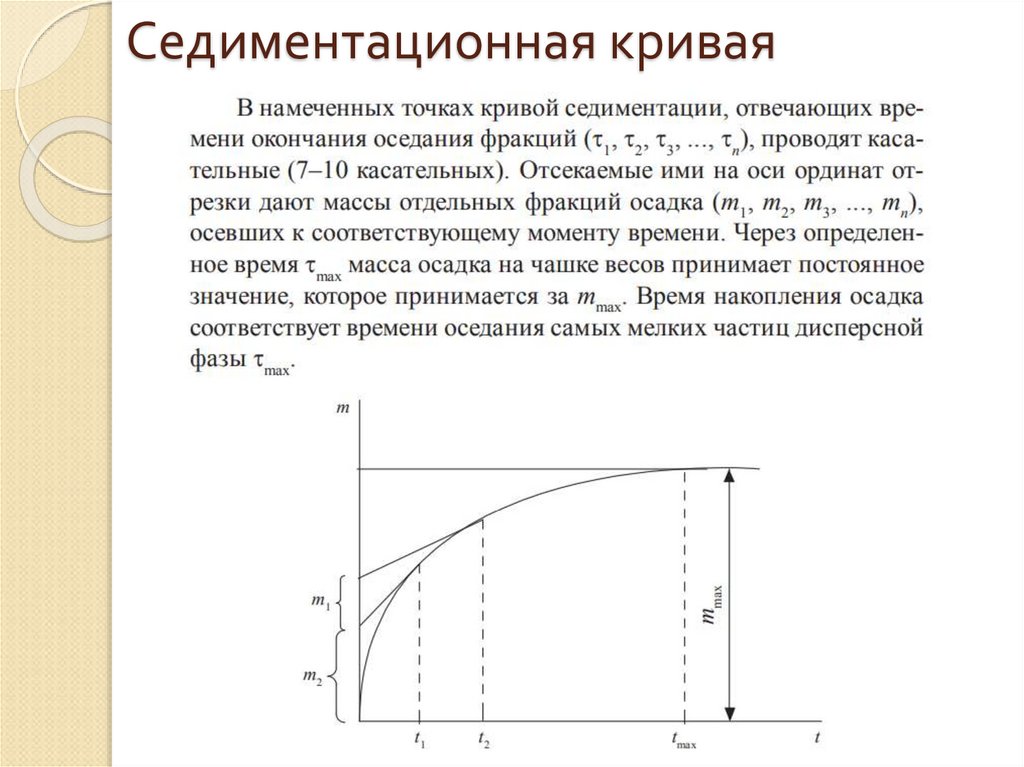
33. Седиментационная кривая

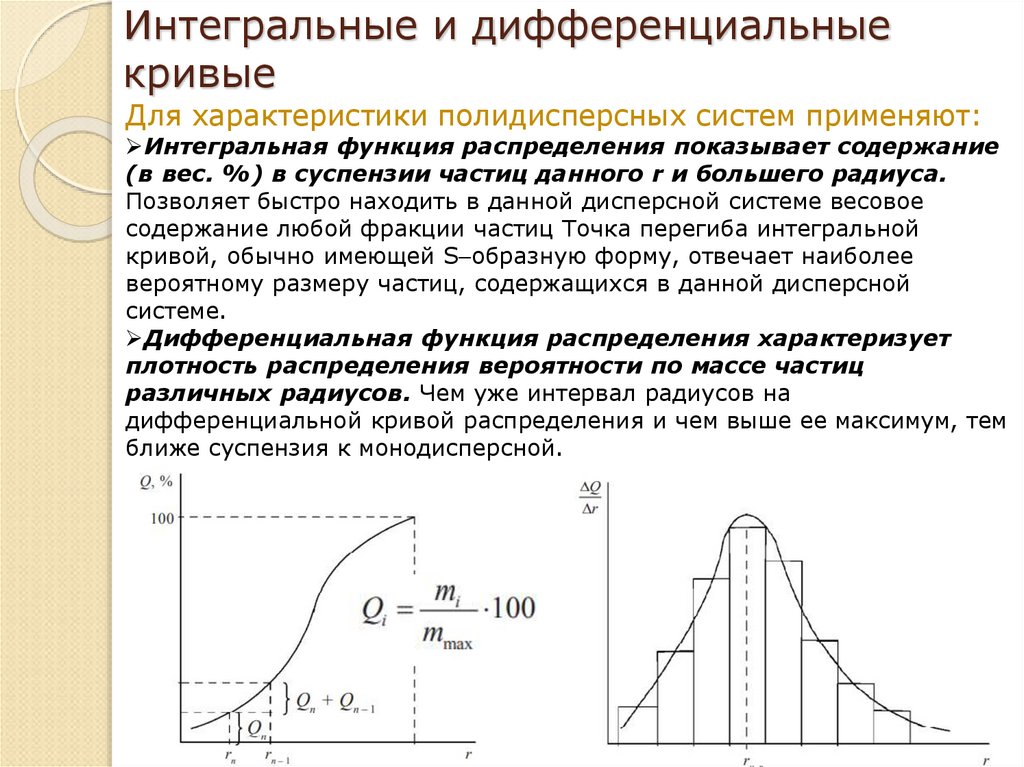
34. Интегральные и дифференциальные кривые

Для характеристики полидисперсных систем применяют:
Интегральная функция распределения показывает содержание
(в вес. %) в суспензии частиц данного r и большего радиуса.
Позволяет быстро находить в данной дисперсной системе весовое
содержание любой фракции частиц Точка перегиба интегральной
кривой, обычно имеющей S образную форму, отвечает наиболее
вероятному размеру частиц, содержащихся в данной дисперсной
системе.
Дифференциальная функция распределения характеризует
плотность распределения вероятности по массе частиц
различных радиусов. Чем уже интервал радиусов на
дифференциальной кривой распределения и чем выше ее максимум, тем
ближе суспензия к монодисперсной.

35.

36.

37. Скоростное ультрацентрифугирование

Существуют два метода определения размеров частиц с
использованием ультрацентрифуги:
•скоростное ультрацентрифугирование;
•равновесное ультрацентрифугирование.
В методе скоростного ультрацентрифугирования применяются
центробежные ускорения порядка 10 5 g ,
седиментационное уравнение принимает вид:
dx
__
2
B
x m 1 V
dt
x - расстояние частицы от оси вращения, - t время.
Константа седиментации
k T
S m 1 V
D
k T S
m
D 1 V
dx
S
dt
x
2
D
k T
B
Этот метод не является абсолютным, так
как требует определения коэффициента
диффузии независимым методом.

38. Равновесное ультрацентрифугирование

При
равновесном
ультрацентрифугировании
используют
ускорения порядка (103 -104)g. При установлении равновесия частицы
располагаются в виде полосы, ширина которой определяется
соотношением процессов седиментации и диффузии. Количество
вещества, переносимого через единицу сечения кюветы, равно
D
1
ic c m 1 V 2 x d
B
__
Обратный поток вещества вследствие диффузии равен
iд D
k T
B
dс
d
dx
В условиях равновесия, после интегрирования от х1 до х2 и от С1 до С2
2 k T ln c 2 c1
__
2
2
2
1 V
x 2 x1
Равновесное ультрацентрифугирование является абсолютным
методом определения масс частиц и макромолекул. Значения масс
вычисляются лишь из разности концентраций на расстоянии и от оси
вращения. При работе методом равновесного ультрацентрифугирования
необходимо проводить ультрацентрифугирование длительное время.
Равновесное
ультрацентрифугирование
связано
с
термодинамической седиментационной устойчивостью (ТСУ). ТСУ не
зависит от вязкости и увеличивается с повышением температуры, т.к. усиливается
тепловое движение частиц.
2
2
c
__ 2 x 2 x1
m 1 V
k T ln 2
2
c1
m

39.

40.

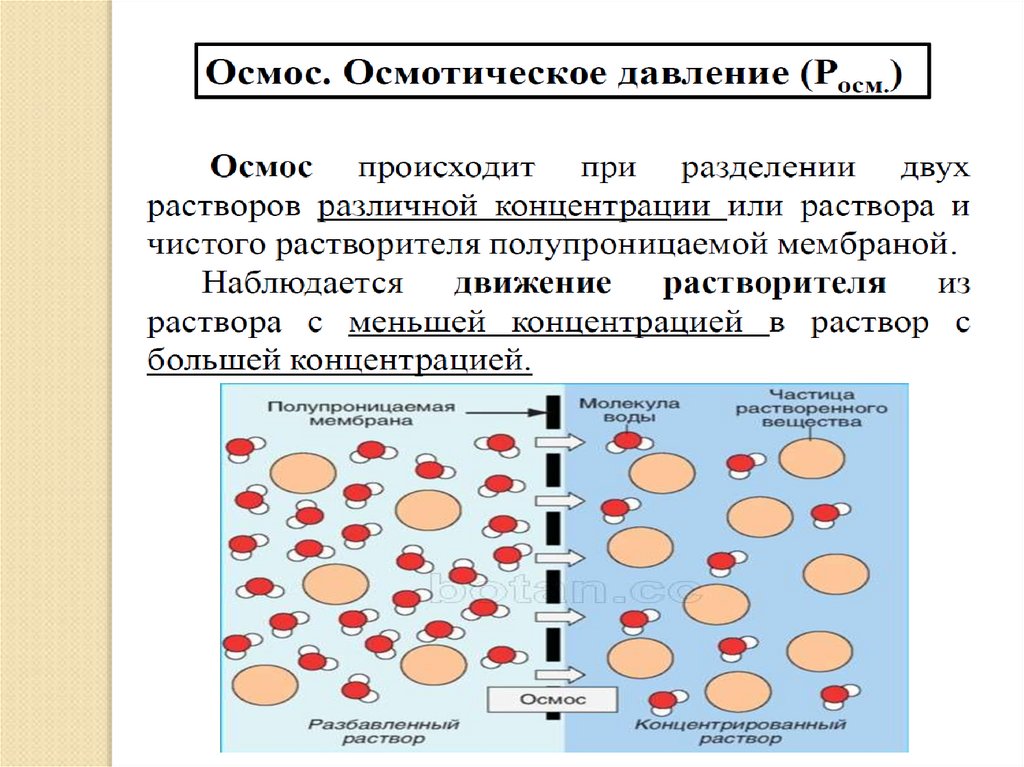
41. Осмотическое давление в коллоидных растворах

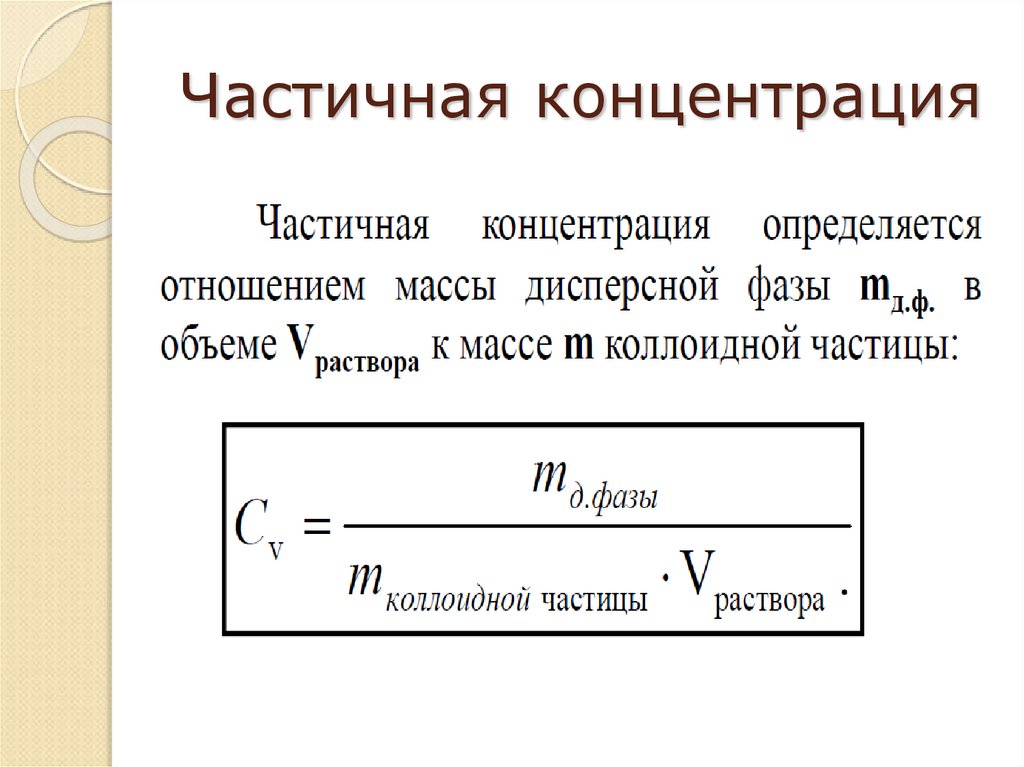
42. Частичная концентрация

43. Осмотическое давление в коллоидных растворах

Значение осмотического давления коллоидных
систем во времени непостоянно.
Причина в агрегации частиц и, как следствие, уменьшении их
общего числа.