1031630

1.

Схема решения задач по теории вероятности
1.
2.
3.
4.
5.
Выяснить, в чем состоит рассматриваемое в задаче
испытание.
Обозначьте буквами события, рассматриваемые в условии
задачи.
С помощью введенных обозначений выразите событие,
вероятность наступления которого необходимо найти.
* Если требуется найти вероятность суммы событий,
выясните, совместны или несовместны рассматриваемые
события.
* Если же требуется найти вероятность произведения
событий, выясните, зависимы или независимы
рассматриваемые события.
Выберите соответствующую условию задачи формулу и
выполните необходимые вычисления.

2.

Формула полной вероятности
Пусть событие A может произойти вместе с одним
из независимых событий B , B , ..., B
Обозначим через A/ B событие - «событие A
i
произошло вместе с .
1
2
n
Bi
Тогда справедлива формула
P A P A / B1 P B1 P A / B2 P B2 P A / Bn P Bn

3.

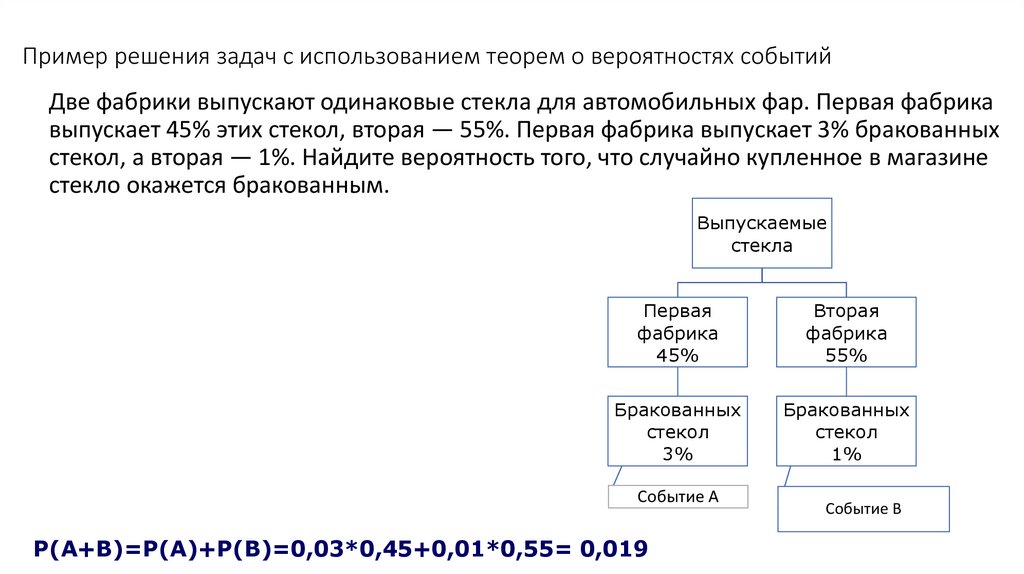
Пример решения задач с использованием теорем о вероятностях событий
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика
выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных
стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине
стекло окажется бракованным.
Выпускаемые
стекла
Первая
фабрика
45%
Вторая
фабрика
55%
Бракованных
стекол
3%
Бракованных
стекол
1%
Событие А
P(A+B)=P(A)+P(B)=0,03*0,45+0,01*0,55= 0,019
Событие В

4.

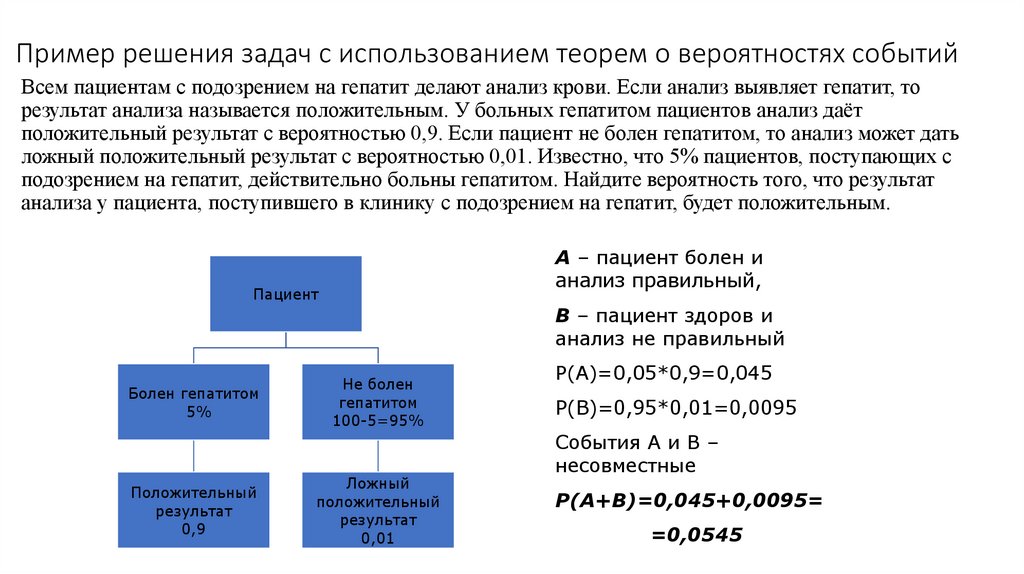
Пример решения задач с использованием теорем о вероятностях событий
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то
результат анализа называется положительным. У больных гепатитом пациентов анализ даёт
положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать
ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с
подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат
анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
A – пациент болен и
анализ правильный,
Пациент
Болен гепатитом
5%
Положительный
результат
0,9
B – пациент здоров и
анализ не правильный
Не болен
гепатитом
100-5=95%
Ложный
положительный
результат
0,01
P(A)=0,05*0,9=0,045
P(B)=0,95*0,01=0,0095
События А и В –
несовместные
P(A+B)=0,045+0,0095=
=0,0545

5.

Пример решения задач с использованием теорем о вероятностях событий
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в
понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того,
что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число
пассажиров будет от 10 до 17.
Количество
пассажиров в
понедельник
Событие А
меньше 10
Событие В
от 10 до 17
Событие А+В
меньше 18
0, 51
х
0,82
События A и B – несовместные, следовательно
0,82=0,51+x. Значит x=0,31

6.

Домашнее задание
Решить задачу
При подозрении на наличие некоторого заболевания пациента
отправляют на ПЦР-тест. Если заболевание действительно есть, то
тест подтверждает его в 91% случаев. Если заболевания нет, то тест
выявляет отсутствие заболевания в среднем в 93% случаев.
Известно, что в среднем тест оказывается положительным у 10%
пациентов, направленных на тестирование.
При обследовании некоторого пациента врач направил его на ПЦРтест, который оказался положительным. Какова вероятность того, что
пациент действительно имеет это заболевание?