2_Preobrazovanie_i_preobrazovateli_izmeritelnoy_informatsii_PiPII

1. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ ПРЕОБРАЗОВАТЕЛЕЙ

Физическая величина Х, характеризующая
объект измерений (температура, давление,
линейное или угловое перемещение и др.),
называется измеряемой величиной.

2. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Совокупность операций, направленных на
установление
численного
значения
физической величины, составляет процесс
измерения.
• Если
при
измерении
используются
электронные средства обработки сигнала,
необходимо
сначала
преобразовать
измеряемый параметр в эквивалентную
электрическую величину, причем сделать это
нужно как можно точнее.

3. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Это значит, что полученная электрическая величина
должна содержать всю информацию об измеряемом
параметре.
• Преобразователь – это устройство, которое,
подвергаясь воздействию физической величины,
выдает эквивалентный сигнал, обычно электрической
природы (заряд, ток, напряжение или комплексное
сопротивление), являющийся функцией измеряемой
величины:
• Y = F(Х),
(2.1)
• где Y – выходная электрическая величина
преобразователя, а X – входная (неэлектрическая)
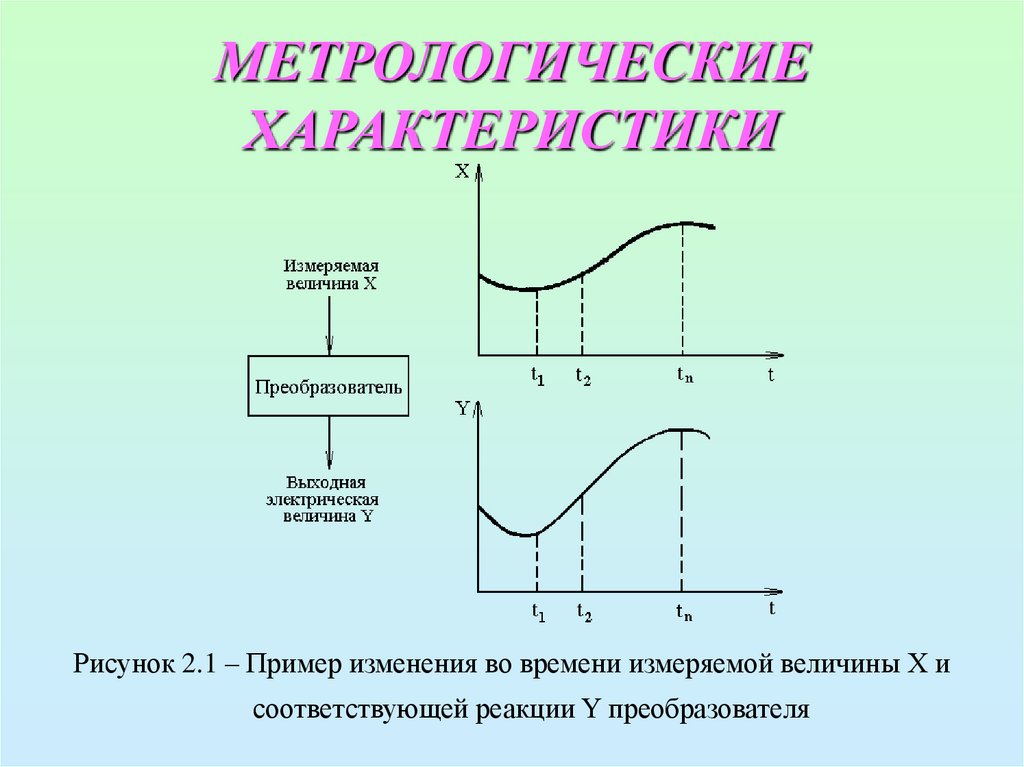
величина (рисунок 2.1).

4. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

Рисунок 2.1 – Пример изменения во времени измеряемой величины X и
соответствующей реакции Y преобразователя

5. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Функция преобразования (ФП) – это
функциональная зависимость выходной
величины измерительного преобразователя от входной, описываемая
аналитическим выражением, в виде
таблиц или графически.
• В аналитически задаваемую функцию
преобразования
обычно
входят
конструктивные параметры преобразователя (датчика).

6. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Измерив значение выходного сигнала Y
преобразователя, можно определить тем
самым значение входной величины X
(рисунок 2.2).
• Соотношение Y=F(X) выражает в общей
теоретической форме физические законы,
положенные
в
основу
работы
преобразователей.

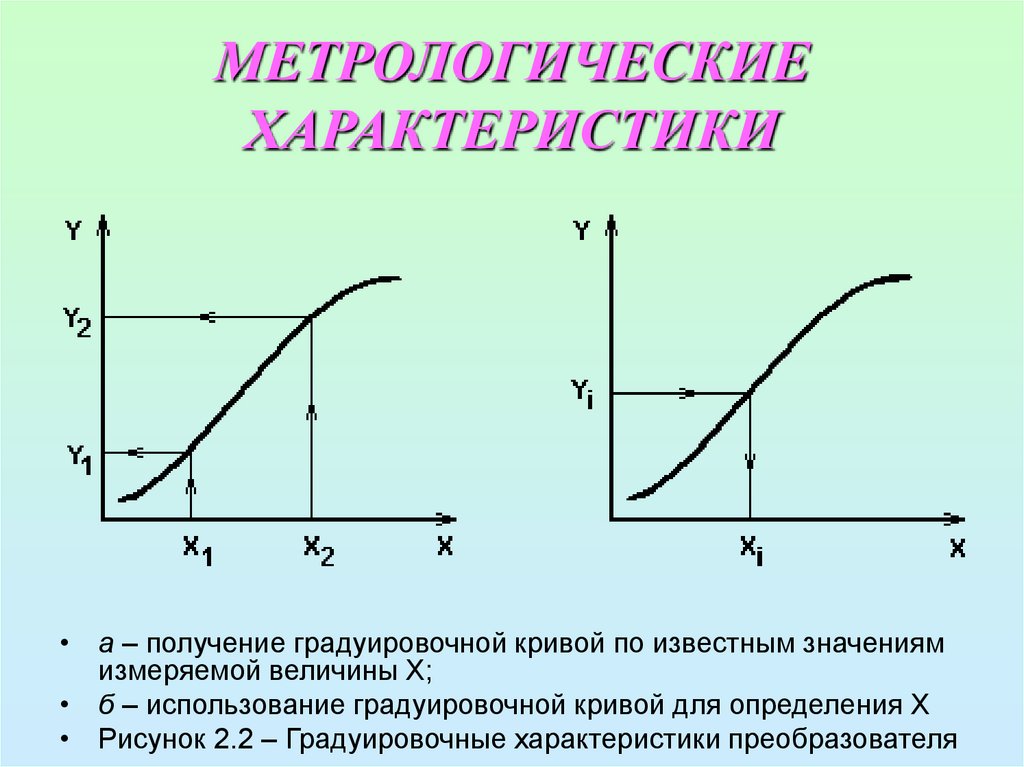
7. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• а – получение градуировочной кривой по известным значениям
измеряемой величины Х;
• б – использование градуировочной кривой для определения Х
• Рисунок 2.2 – Градуировочные характеристики преобразователя

8. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Для
всех
преобразователей
функция
преобразования
• – соотношение Y = F(X) –
• в
численной
форме
определяется
экспериментально в результате градуировки.
• В этом случае для ряда точно известных
значений X измеряют соответствующие
значения Y, что позволяет построить
градуировочную кривую (рисунок 2.2,а).
• Из этой кривой для всех полученных в
результате измерения значений Y можно
найти соответствующие значения искомой
величины X (рисунок 2.2,б).

9. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Чаще
всего
стремятся
функцию
преобразования сделать линейной, т.е.
установить прямую пропорциональность между изменением входной
величины
Y
и
соответствующим
приращением выходной величины X
преобразователя.

10. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Для
описания
линейной
функции
преобразования Y = F(X) = Y0 + S X
достаточно двух параметров: начального
значения выходной величины Y0 (нулевого
уровня), соответствующего нулевому (или
какому-либо
другому
характерному)
значению входной величины X, и показателя
относительного
наклона
характеристики,
называемого чувствительностью преобразователя
Y
S
X

11. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Чувствительность преобразователя –
свойство
преобразователя,
определяемое отношением изменения
выходной величины измерительного
преобразователя к вызывающему ее
изменению входной величины.
• Как правило, это именованная величина
с
разнообразными
единицами,
зависящими от природы входной и
выходной величин.

12. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Для
реостатного
преобразователя,
например,
• единица чувствительности – Ом/мм,
• для термопары – мВ/К,
• для фотоэлемента – мкА/лм,
• для двигателя – об/(с В) или Гц/В,
• для гальванометра – мм/мкА и т.д.

13. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Важнейшей проблемой при проектировании и
использовании преобразователя является
обеспечение постоянства чувствительности,
которая должна как можно меньше зависеть
от значений Х (определяя линейность
характеристики преобразования) и частоты
их изменений, от времени и от воздействия
других
физических
величин,
характеризующих не сам объект, а его
окружение (они называются влияющими на
результаты измерений величинами).

14. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Однако
чувствительность
каждого
преобразователя постоянна только на
определенном
участке
функции
преобразования, который ограничивается с
одной стороны пределом преобразования, а
с другой – порогом чувствительности.
• Предел
преобразования
данного
преобразователя – это максимальное
значение входной величины, которое еще
может быть им воспринято без искажения и
без повреждения преобразователя.

15. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• Порог чувствительности – это
минимальное
изменение
значения
входной величины, способное вызвать
заметное
изменение
выходной
величины преобразователя.
• Значение порога чувствительности
принято определять равным половине
полосы
неоднозначности
функции
преобразования при малых значениях
входной величины.

16. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ

• При
нелинейной
функции
преобразования
чувствительность
зависит
от
значения
входной
величины.

17. Погрешности измерительных преобразователей

• Важной
характеристикой
любого
измерительного преобразователя является
его основная погрешность, которая может
быть обусловлена
• принципом действия,
• несовершенством конструкции
• или технологии его изготовления
• и проявляется при нормальных значениях
влияющих величин или нахождении их в
пределах нормальной области.

18. Погрешности измерительных преобразователей

• Основная
погрешность
измерительного
преобразователя может иметь несколько
составляющих, обусловленных:
• неточностью образцовых средств измерений,
с
помощью
которых
проводилось
определение функции преобразования;
• отличием
реальной
градуировочной
характеристики от номинальной функции
преобразования;

19. Погрешности измерительных преобразователей

• приближенным (табличным, графическим,
аналитическим)
выражением
функции
преобразования;
• неполным
совпадением
функции
преобразования при возрастании и убывании
измеряемой
неэлектрической
величины
(гистерезис функции преобразования);
• неполной
воспроизводимостью
характеристик
измерительного
преобразователя
(чаще всего чувствительности).

20. Погрешности измерительных преобразователей

• При градуировке серии однотипных
преобразователей оказывается, что их
характеристики несколько отличаются
друг от друга, занимая некоторую
полосу.
• Поэтому
в
формуляре
на
измерительный
преобразователь
приводится
некоторая
средняя
характеристика,
называемая
номинальной.

21. Погрешности измерительных преобразователей

• Разности между номинальной (паспортной) и
реальной характеристиками преобразователя
рассматриваются как его погрешности.
• Для
преобразователей
определение
абсолютных и относительных погрешностей
несколько сложнее.
• Они определяются по входу ВХ и выходу
ВЫХ и характеризуют отличие реальной
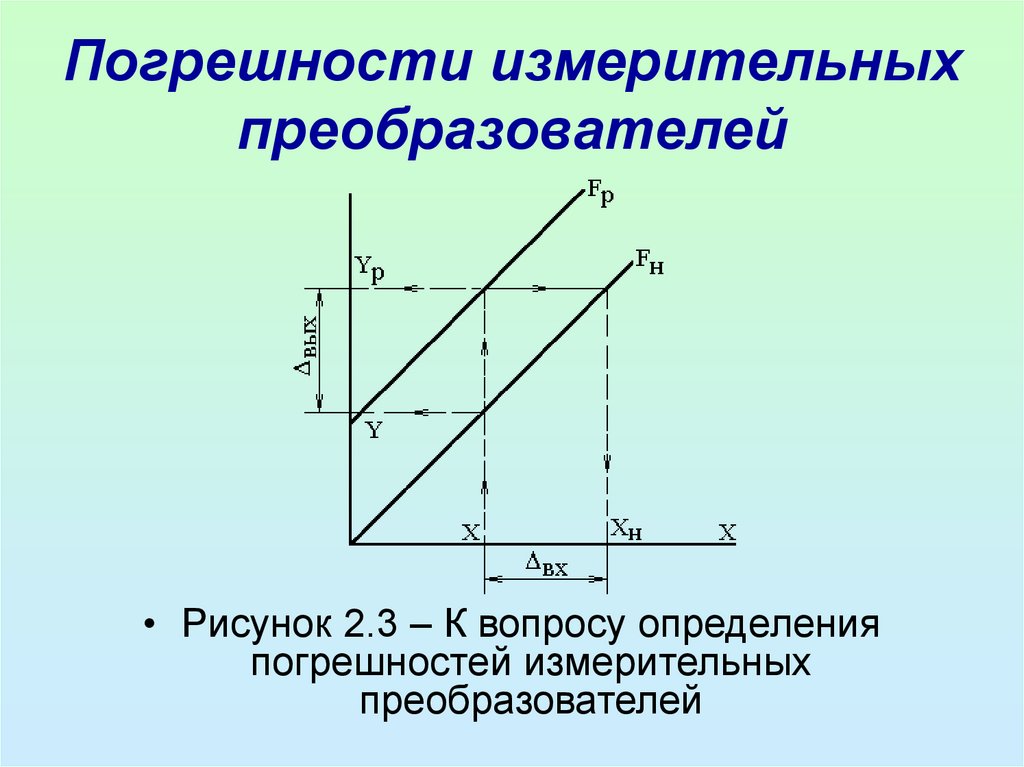
характеристики преобразования YР = FР(X) от
номинальной YН = FН(X) (рисунок 2.3).

22. Погрешности измерительных преобразователей

• Для оценки погрешности по выходу находят
значения YР и YН при заданном значении
входной величины X. Тогда ВЫХ = YР - YН, а
относительная погрешность = ВЫХ/YР.
• По входу ВХ = ХН – Х, где ХН = FН-1(YР)
определяется через значение YР и функцию,
обратную FН, т.е. XН – такое значение X,
которое при номинальной характеристики
дало бы на входе значение YР;
• = ВХ/Х – относительная погрешность.

23. Погрешности измерительных преобразователей

• Рисунок 2.3 – К вопросу определения
погрешностей измерительных
преобразователей

24. Погрешности измерительных преобразователей

• Погрешности
измерительных
преобразователей в целом аналогичны
погрешностям
СИ
электрических
величин.
• По характеру поведения во времени
погрешности бывают
• систематические,
• случайные
• и промахи (грубые погрешности).

25. Погрешности измерительных преобразователей

• В зависимости от условий эксплуатации –
• основные
(для
нормальных
условий
эксплуатации) и
• дополнительные (при выходе влиявших
величин за пределы нормальных областей).
• Причинами
основной
могут
быть
идеализация принципа действия, неточность
градуировки,
невоспроизводимость
от
экземпляра
к
экземпляру
ФП,
несовершенство конструктивного исполнения
ИП.

26. Погрешности измерительных преобразователей

• Дополнительные
погрешности
определяются в первую очередь тем,
насколько при разработке, изготовлении
и эксплуатации ИП удалось "подавить"
воздействие мешающих факторов на
фоне естественной входной величины.

27. Погрешности измерительных преобразователей

• В зависимости от скорости изменения
измеряемой
величины
различают
статические и динамические погрешности.
• Статические не зависят от скорости
изменения,
• а динамические зависят и равны нулю при
равной нулю скорости.
• Таким образом, динамические погрешности
определяются инерционными свойствами ИП.

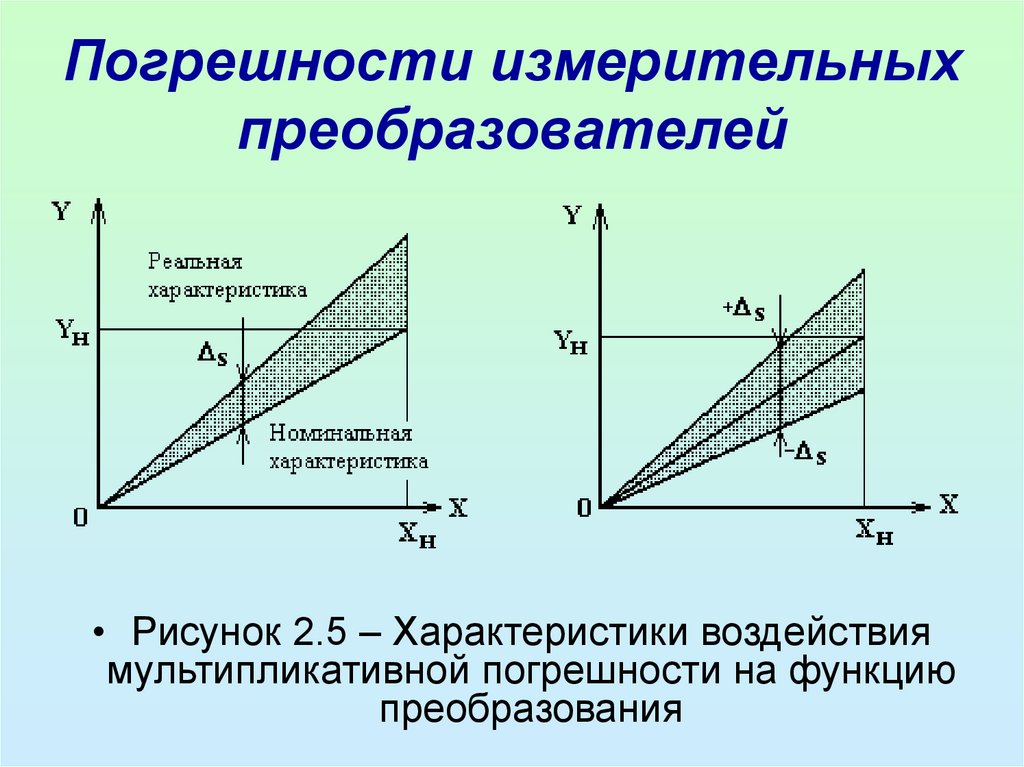
28. Погрешности измерительных преобразователей

• По
характеру
зависимости
погрешностей
от
преобразуемой
величины X различают
• аддитивные и
• мультипликативные,
• проявляющиеся в искажении характера
функции преобразования.

29. Погрешности измерительных преобразователей

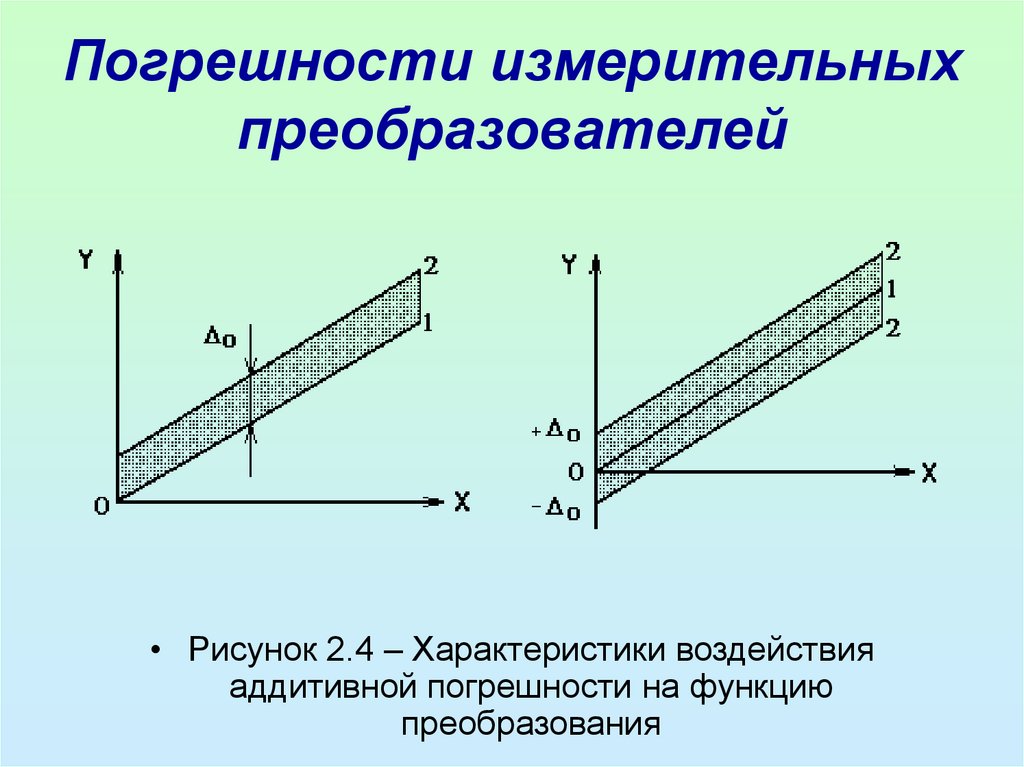
• Аддитивными (погрешности смещения нуля)
называются погрешности, значения которых
не зависят от преобразуемой физической
величины.
• При их наличии реальная 2 характеристика
преобразователя
смещена
относительно
номинальной 1 вверх (вниз) на постоянное
значение (рисунок 2.4,а) и выходная
величина Y для всех Х оказывается больше
(меньше) на 0.

30. Погрешности измерительных преобразователей

• Рисунок 2.4 – Характеристики воздействия
аддитивной погрешности на функцию
преобразования

31. Погрешности измерительных преобразователей

• Погрешность
нуля
может
быть
как
систематической, так и случайной. В первом
случае ее можно компенсировать путем
введения в прибор специальной регулировки
для установки нуля.
• Во
втором
случае
(рисунок
2.4,б)
скорректировать её нельзя и ФП смещается
случайным образом параллельно самой
себе,
образуя
постоянную
полосу
погрешностей ± 0(2 0).

32. Погрешности измерительных преобразователей

• Примером систематической аддитивной
погрешности
может
служить
погрешность
из-за
неточности
установки нуля перед измерением.
• Примером случайной – погрешность изза посторонних электрических наводок
на линейные цепи.

33. Погрешности измерительных преобразователей

• Мультипликативными
(погрешности
чувствительности) называются погрешности,
пропорциональные
значениям
преобразуемой величины.
• При этом изменяется крутизна функции
преобразования
(рисунок
2.5),
т.е.
чувствительность и реальная характеристика
преобразователя
2
отличаются
от
номинальной 1 на значение S(X) (рисунок
2.5,а) или образуют полосу погрешностей
± S(Х) при их случайном характере (рисунок
2.5,б).

34. Погрешности измерительных преобразователей

• Рисунок 2.5 – Характеристики воздействия
мультипликативной погрешности на функцию
преобразования

35. Погрешности измерительных преобразователей

• Примером систематической мультипликативной погрешности может служить
изменение коэффициента передачи
потенциометрической
цепи
с
резистивными ИП вследствие старения.
• Примером случайной – погрешность изза посторонних электрических наводок
на нелинейную цепь.

36. Погрешности измерительных преобразователей

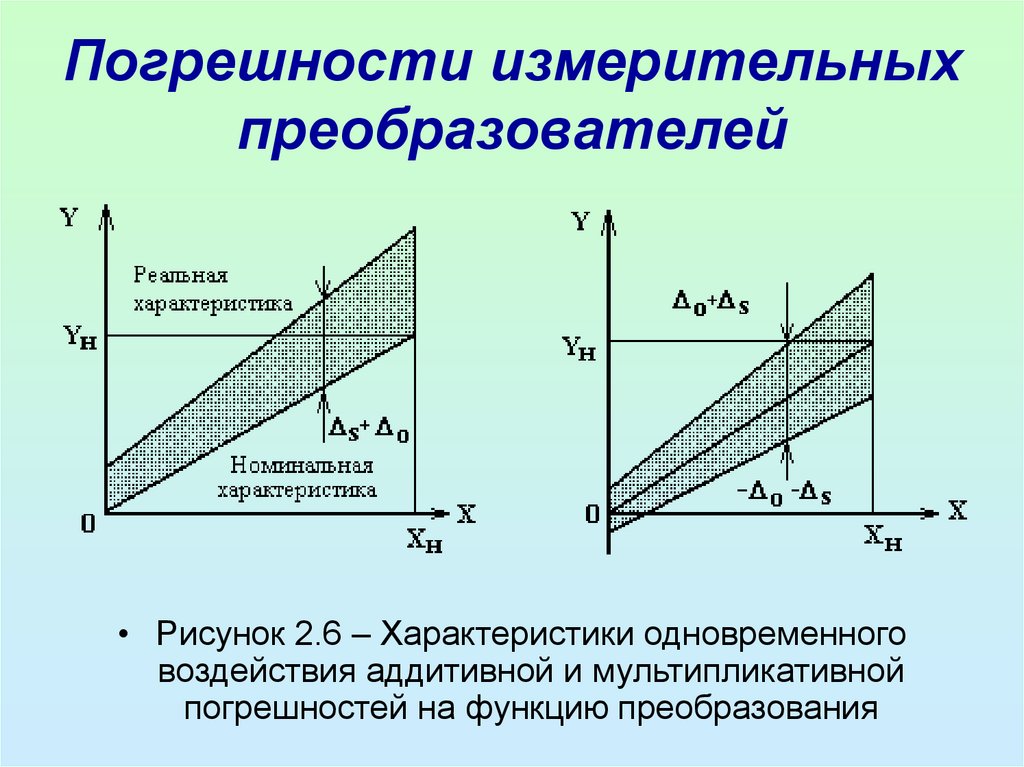
• В большинстве реальных преобразователей
аддитивная
и
мультипликативная
составляющие погрешности присутствуют
одновременно.
• В
результате
полоса
погрешностей
распределяется так, как показано на рисунке
2.6.
• При обработке результатов аддитивные и
мультипликативные
составляющие
погрешности суммируются геометрически как
некоррелированные составляющие.

37. Погрешности измерительных преобразователей

• Рисунок 2.6 – Характеристики одновременного
воздействия аддитивной и мультипликативной
погрешностей на функцию преобразования

38. Погрешности измерительных преобразователей

• Для
дискретных
ИП
(например,
реостатные проволочные) характерна
еще
одна
разновидность
–
погрешность квантования.
• Эта погрешность возникает во всех
дискретных устройствах, в том числе в
цифровых
измерительных
преобразователях.

39. Погрешности измерительных преобразователей

• Аналогично СИ электрических величин погрешности
СИ
неэлектрических
величин
могут
быть
представлены в виде абсолютной, относительной
или приведенной погрешности.
• К числу важнейших параметров ИП относится порог
чувствительности,
под
которым
понимается
значение преобразуемой (измеряемой) величины X0,
численно равное значению аддитивной погрешности.
• Таким
образом,
порог
чувствительности
определяется погрешностью смещения нуля и
ограничивается, как правило, собственными шумами
преобразователя.

40. Погрешности измерительных преобразователей

• Другим
параметром,
связанным
с
погрешностями,
является
предел
преобразования (предел измерения) Xk, то
есть
максимальное
значение
входной
величины, которое может преобразовать ИП
без существенных искажений.
• Интервал значений от X0 до Xk, в котором
погрешность не превышает 10 %, называется
полным диапазоном преобразования данного
преобразователя.

41. Погрешности измерительных преобразователей

• В полном диапазоне проводить измерения
нецелесообразно, так как
на его краях
абсолютная
погрешность
измерения
достигает 100 %, т.е. результат измерения не
определен.
• Поэтому вводится понятие рабочий диапазон
преобразований (измерений), в пределах
которого
удовлетворяются
заданные
требования к точности преобразования.
• Таким образом, верхний предел рабочего
диапазона определяется мультипликативной
составляющей погрешности.

42. Погрешности измерительных преобразователей

• Градуировка
измерительного
преобразователя
(определение
реальной функции преобразования)
производится
с
использованием
средств измерений неэлектрических и
электрических величин.
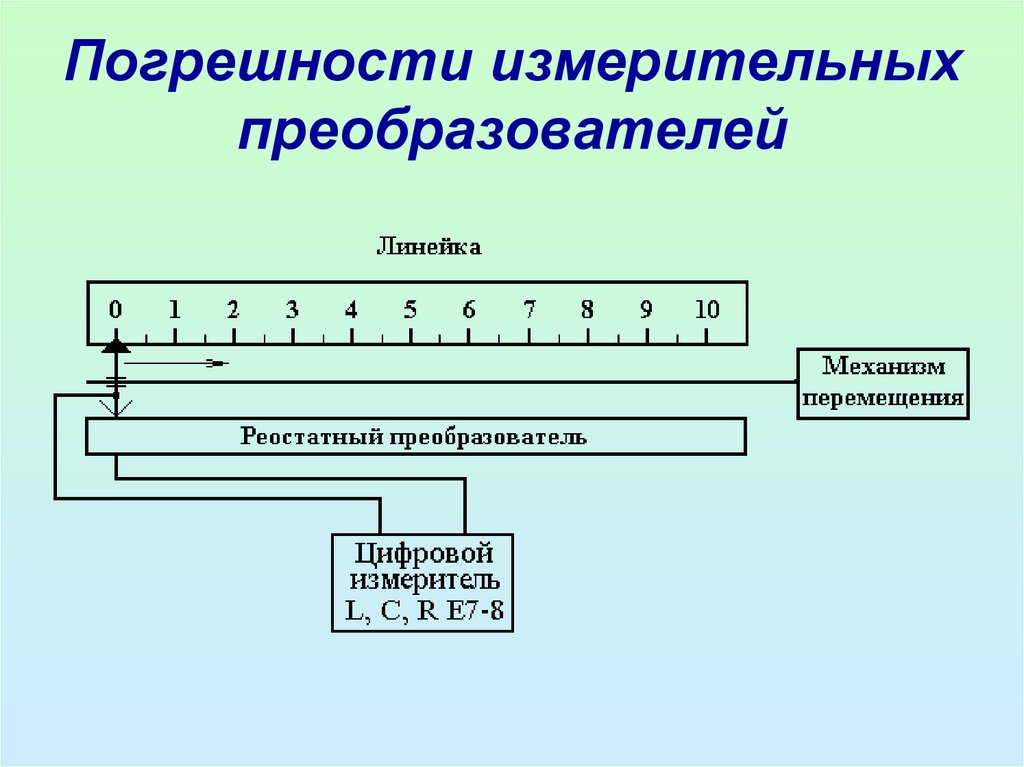
• Структурная схема установки для
градуировки
реостатного
преобразователя
представлена
на
рисунке 2.

43. Погрешности измерительных преобразователей

44. Погрешности измерительных преобразователей

• В
качестве
средства
измерения
линейного
перемещения
(неэлектрической
величины)
используется линейка, а средства
измерения электрической величины –
активного сопротивления – цифровой
измеритель L, C, R – E7-8.

45. Погрешности измерительных преобразователей

• Процесс
градуировки
преобразователя
заключается в следующем.
• С
помощью
механизма
перемещения
подвижный контакт (движок) реостатного
преобразователя
последовательно
устанавливается на оцифрованные отметки
шкалы линейки и на каждой отметке
производится
измерение
активного
сопротивления преобразователя с помощью
прибора Е7-8.
• Измеренные
значения
линейного
перемещения и активного сопротивления
заносятся в градуировочную таблицу 1.

46. Погрешности измерительных преобразователей

• В
этом
случае
получаем
функцию
преобразования
измерительного
преобразователя, заданную в табличной
форме.
• При получении графического изображения
функции
преобразования
необходимо
воспользоваться
рекомендациями,
приведенными на рисунке 1,а.

47. Погрешности измерительных преобразователей

• Но при этом следует иметь в виду, что измерение
линейного перемещения и активного сопротивления
произведено
с
погрешностью,
обусловленной
инструментальными погрешностями используемых
средств измерений.
• В связи с этим и определение функции
преобразования произведено также с погрешностью
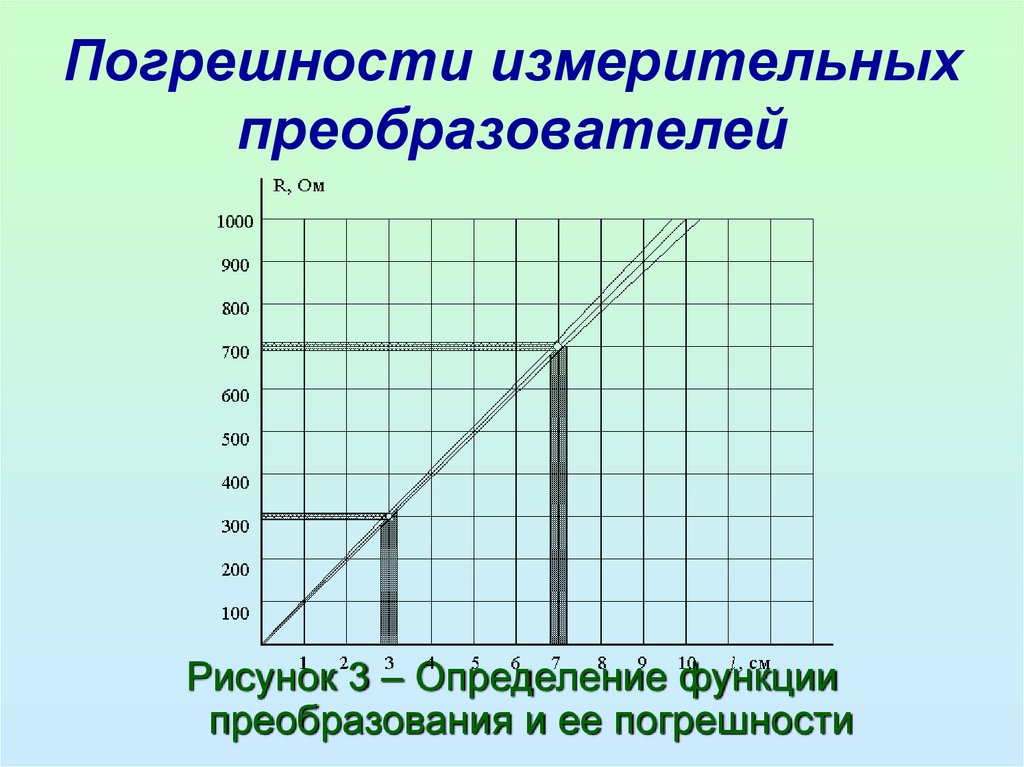
(рисунок 3).
• Поскольку определение функции преобразования
проводилось путем косвенных измерений, то и
оценка ее погрешности должна проводиться как
погрешности результата косвенного измерения по
формуле

48. Погрешности измерительных преобразователей

2
F
F
ФП
Y
X
Y
X
2

49. Погрешности измерительных преобразователей

• где
F
Y
F
Х
частные производные;
• Y, X – инструментальные
погрешности средств измерений.

50. Погрешности измерительных преобразователей

Рисунок 3 – Определение функции
преобразования и ее погрешности