Similar presentations:
Треугольник Серпинского
1.
Треугольник Серпинского2.
Треугольник СерпинскогоЭто фрактал, который получается из треугольника путём
рекурсивного деления его на меньшие треугольники. На каждом шаге
каждый треугольник заменяется на ещё три равносторонних
треугольника меньшего размера. Этот процесс повторяется до
бесконечности для каждого из меньших треугольников, которые
остались.
3.
ВацлавСерпинский
(14.03.1882 21.10.1969)
Польский математик. Известен трудами в
области теории множеств, теории чисел,
теории функций и топологии.
В математике известны и «треугольник
Серпинского»
и также «ковер Серпинского» в виде
непрерывной кривой, проходящей через
каждую точку квадрата
4.
Некоторые свойства треугольникаСерпинского
5.
Бесконечность
Процесс
рекурсивного
деления треугольника
повторяется до
бесконечности, что
приводит к бесконечному
числу мелких
треугольников в
структуре.
6.
ПлотностьТреугольник заполняет
всё пространство внутри
исходного треугольника,
но при этом имеет
конечную площадь, так
как его размер
уменьшается с каждой
итерацией.
7.
Фрактальность
Треугольник
Серпинского
обладает
сложной и
повторяющейс
я структурой
на
всех
уровнях
масштаба.
8.
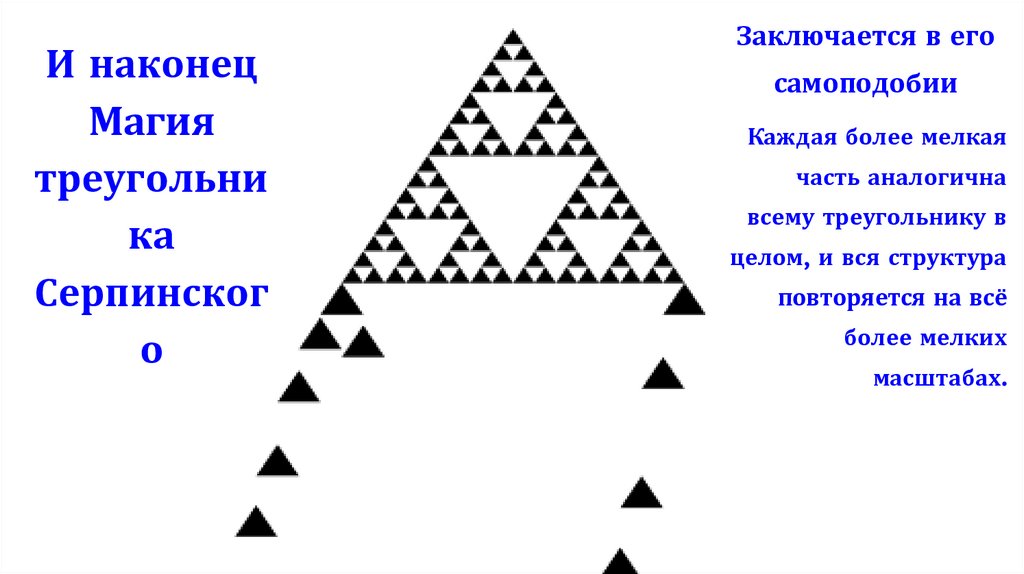
И наконецМагия
треугольни
ка
Серпинског
о
Заключается в его
самоподобии
Каждая более мелкая
часть аналогична
всему треугольнику в
целом, и вся структура
повторяется на всё
более мелких
масштабах.
9.
10.
ТреугольникСерпинского
находит
применение в
различных
областях
11.
Компьютерная графика и анимацияТреугольник
Серпинского
используют для
создания узоров и
текстур, а также
для генерации
фрактальных
ландшафтов и
фоновых
изображений в
компьютерной
графике и
анимации











 mathematics
mathematics








