презентация

1.

Свободные колебания.
Гармоничные колебания.
Затухающие и вынужденные
колебания

2.

Что общего между
движением на этих
фотографиях?

3.

Колебание – повторяющийся с
течением времени какой–либо
процесс

4.

Открыл соотношение
между длиной маятника и
временем каждого
качания.
Изобрел первые часы с
маятником и нашел центр
качания физического
маятника.

5.

Гюйгенс изобрел первые часы с маятником (1657) и
во втором издании своей монографии «Маятниковые
часы» (1673) исследовал ряд проблем, связанных с
движением маятника, в частности нашел центр
качания физического маятника.

6.

Большой вклад в изучение колебаний внесли многие ученые:
английские – У. Томсон (лорд Кельвин) и Дж. Рэлей,
русские – А.С. Попов и П.Н. Лебедев,
советские – А.Н. Крылов, Л.И. Мандельштам, Н.Д. Папалекси

7.

Колебания
бывают
механические,
электромагнитные,
химические,
термодинамические и
различные
другие.
Несмотря
на
такое
разнообразие, все они
имеют между собой
много
общего.

8.

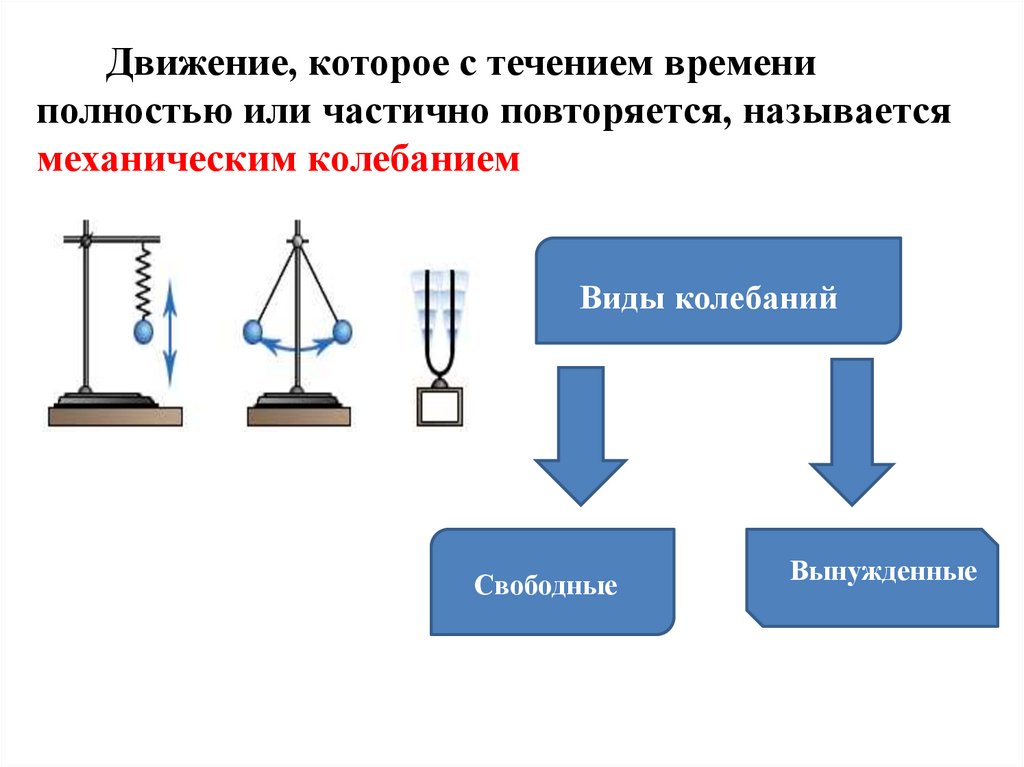
Движение, которое с течением времени
полностью или частично повторяется, называется
механическим колебанием
Виды колебаний
Свободные
Вынужденные

9.

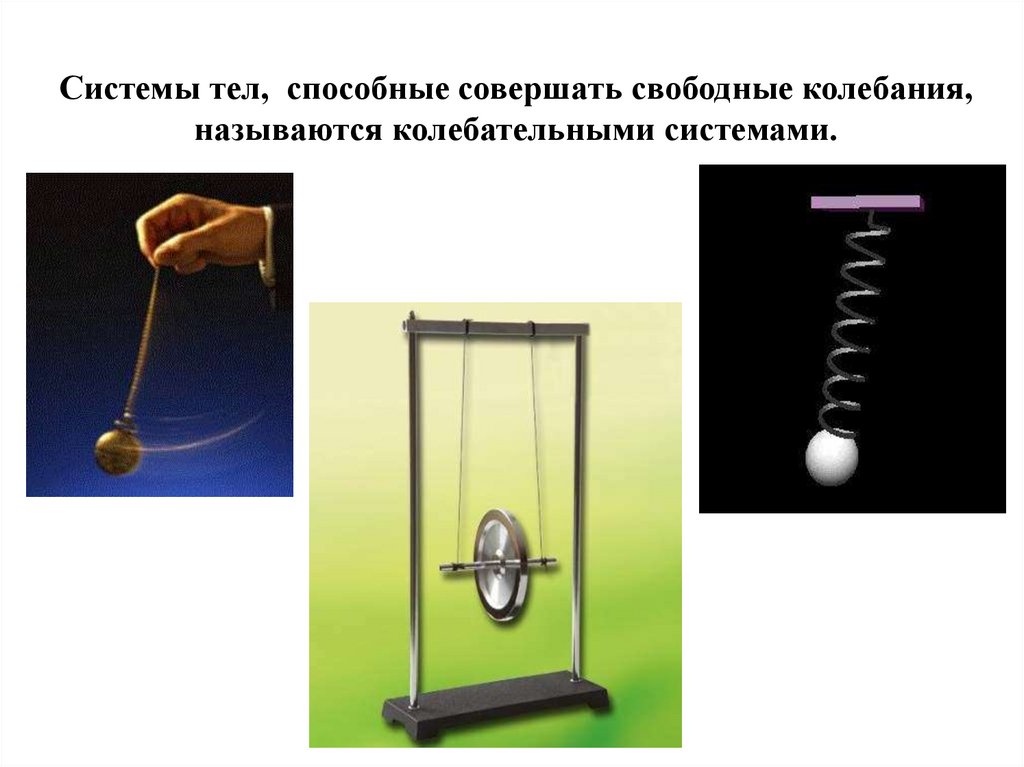
Системы тел, способные совершать свободные колебания,
называются колебательными системами.

10.

Маятником называют твердое тело,
совершающее под действием приложенных к
нему сил колебания около неподвижной точки
или вокруг оси.
Виды маятников
пружинный
нитяной

11.

Маятник Фуко
Первая публичная
демонстрация была
осуществлена в 1851 г. В
Парижском Пантеоне

12.

Маятники Максвелла и Обербека

13.

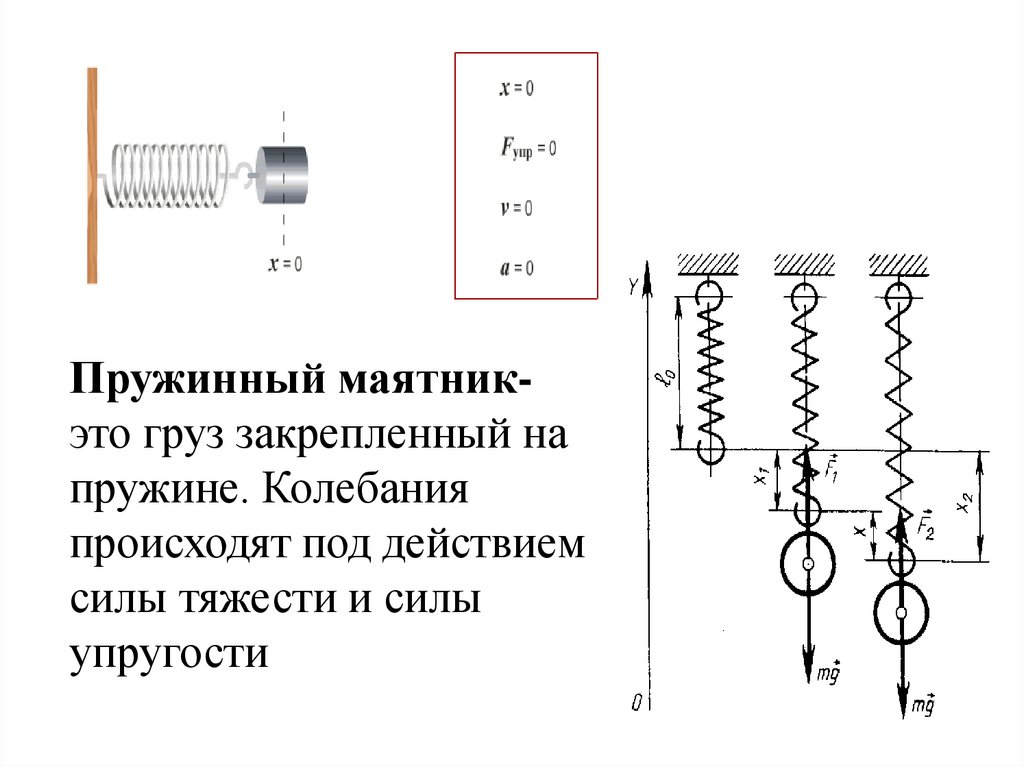
Пружинный маятникэто груз закрепленный на
пружине. Колебания
происходят под действием
силы тяжести и силы
упругости

14.

Уравнение свободных колебаний
пружинного маятника.
где ах – ускорение, т - масса, х смещение пружины, k – жесткость
пружины.

15.

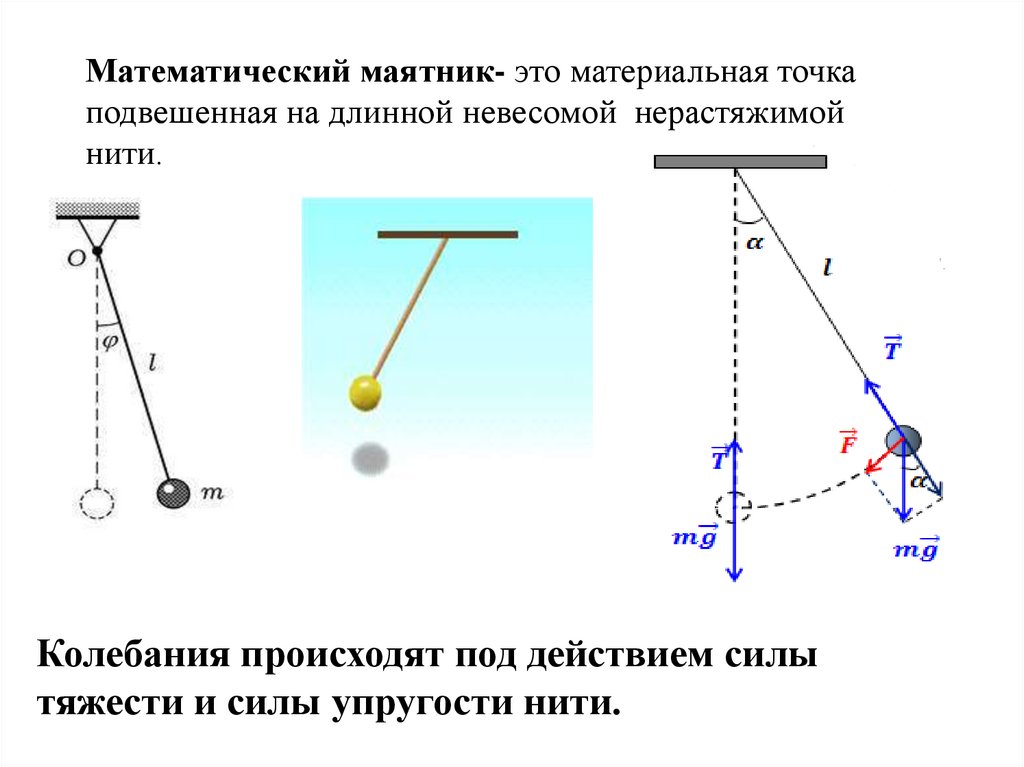
Математический маятник- это материальная точка
подвешенная на длинной невесомой нерастяжимой
нити.
Колебания происходят под действием силы
тяжести и силы упругости нити.

16.

Уравнение свободных колебаний
математического маятника
где ах – ускорение, g – ускорение
свободного падения, х - смещение, l –
длина нити маятника.

17.

Основные характеристики колебания

18.

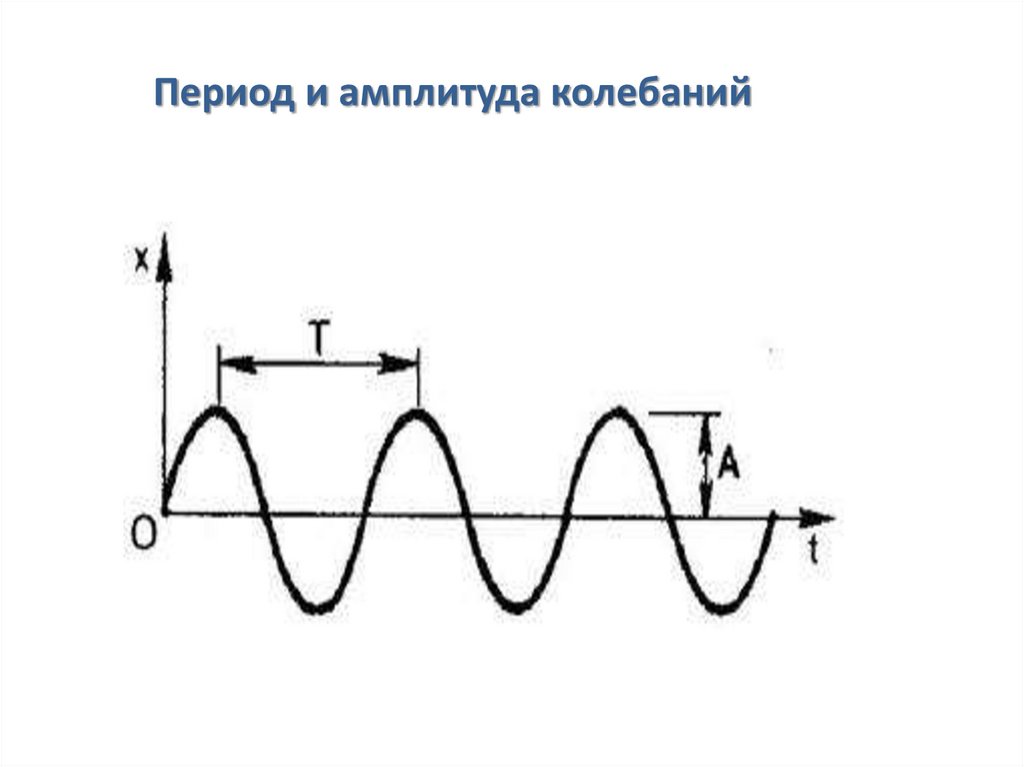
Период и амплитуда колебаний

19.

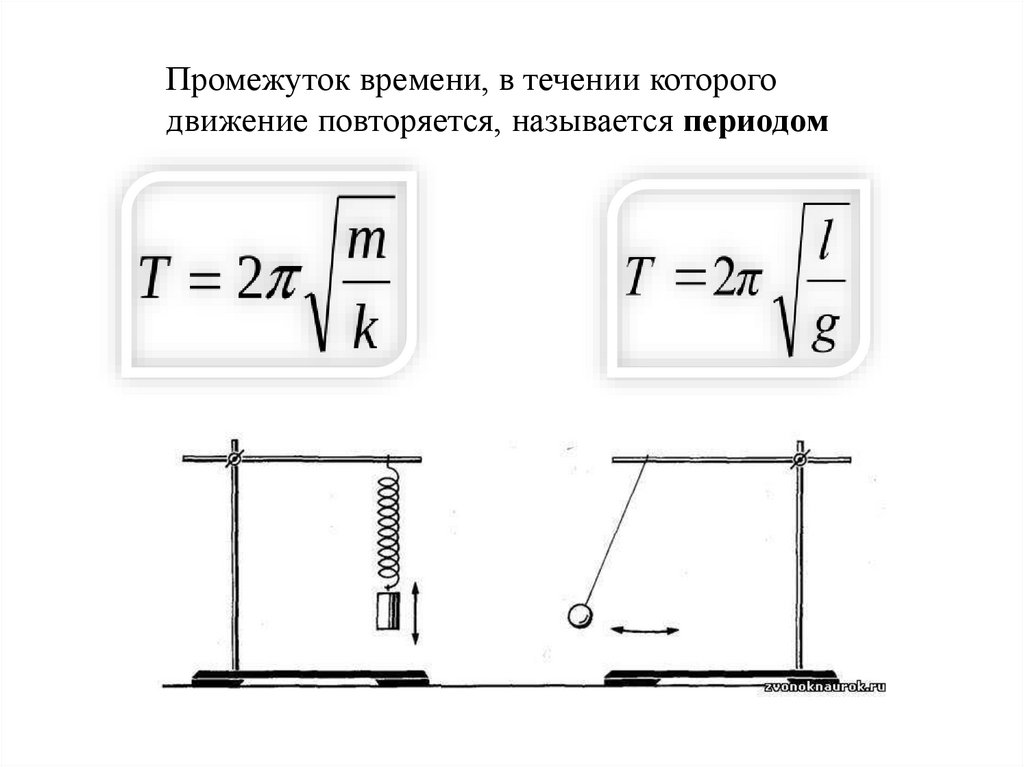
Промежуток времени, в течении которого
движение повторяется, называется периодом

20.

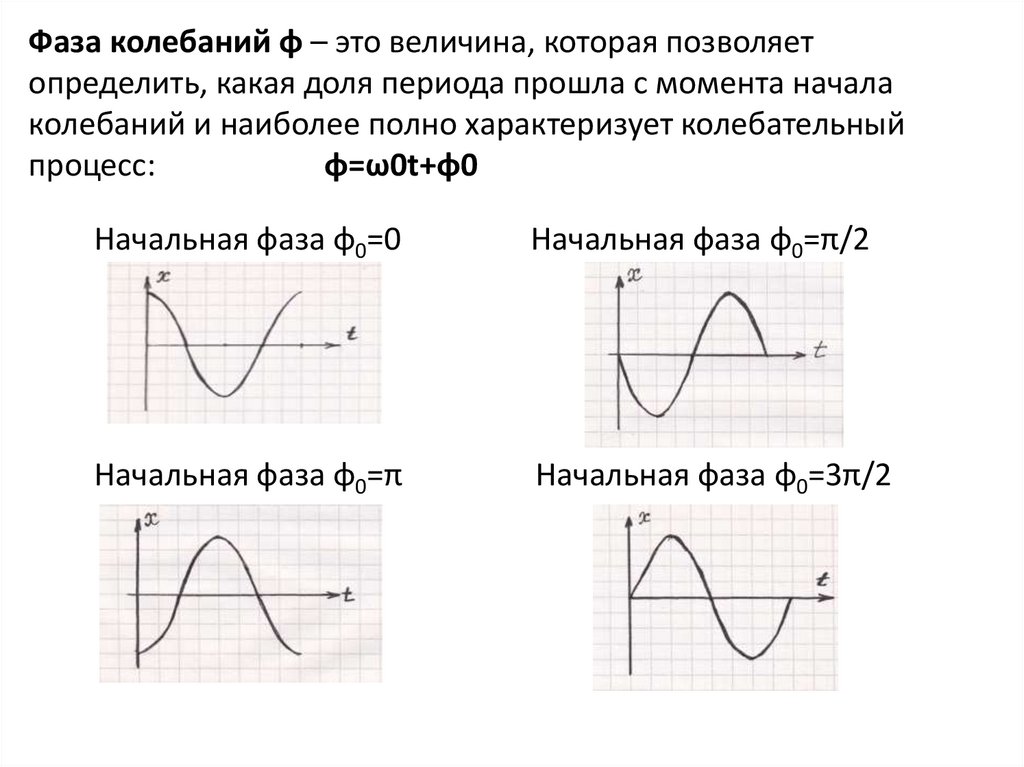
Фаза колебаний φ – это величина, которая позволяет
определить, какая доля периода прошла с момента начала
колебаний и наиболее полно характеризует колебательный
процесс:
φ=ω0t+φ0
Начальная фаза φ0=0
Начальная фаза φ0=π/2
Начальная фаза φ0=π
Начальная фаза φ0=3π/2

21.

Уравнение гармонических
колебаний
Гармонические колебания – это колебания,
происходящие по закону синуса или косинуса
Xm – амплитуда колебаний
x = xm cos (ωt + φ0)
φ0 – начальная фаза колебаний
ω – циклическая частота
ω=2πν
φ = ωt + φ0 – фаза колебаний в
данный момент времени

22.

Силы, действующие между
телами системы, называют
внутренними
Силы, действующие на тела
системы со стороны тел, не
входящих в нее, называют
внешними

23.

Свободными колебаниями называются
колебания в системе под действием
внутренних сил, после того как система
выведена из положения равновесия.
С течением времени свободные
колебания вследствие трения
затухают.

24.

Системы тел, которые
способны совершать
свободные колебания,
называются
колебательными
системами

25.

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
• Вынужденные колебания -колебания, происходящие под
действием внешней периодической силы.
• Внешняя периодическая сила, называемая вынуждающей,
сообщает колебательной системе дополнительную
энергию, которая идет на восполнение энергетических
потерь, происходящих из-за трения.
• Если вынуждающая сила изменяется во времени по
закону синуса или косинуса, то вынужденные колебания
будут гармоническими и незатухающими.

26.

• Частота вынужденных колебаний равна
частоте вынуждающей силы. В случае, когда
частота вынуждающей силы υ совпадает с
собственной частотой колебательной системы
υ0, происходит резкое возрастание амплитуды
вынужденных колебаний — резонанс.
• Резонанс возникает из-за того, что при υ =
υ0 внешняя сила, действуя в такт со
свободными колебаниями, все время со
направлена со скоростью колеблющегося тела
и совершает положительную работу: энергия
колеблющегося тела увеличивается, и
амплитуда его колебаний становится
большой.

27.

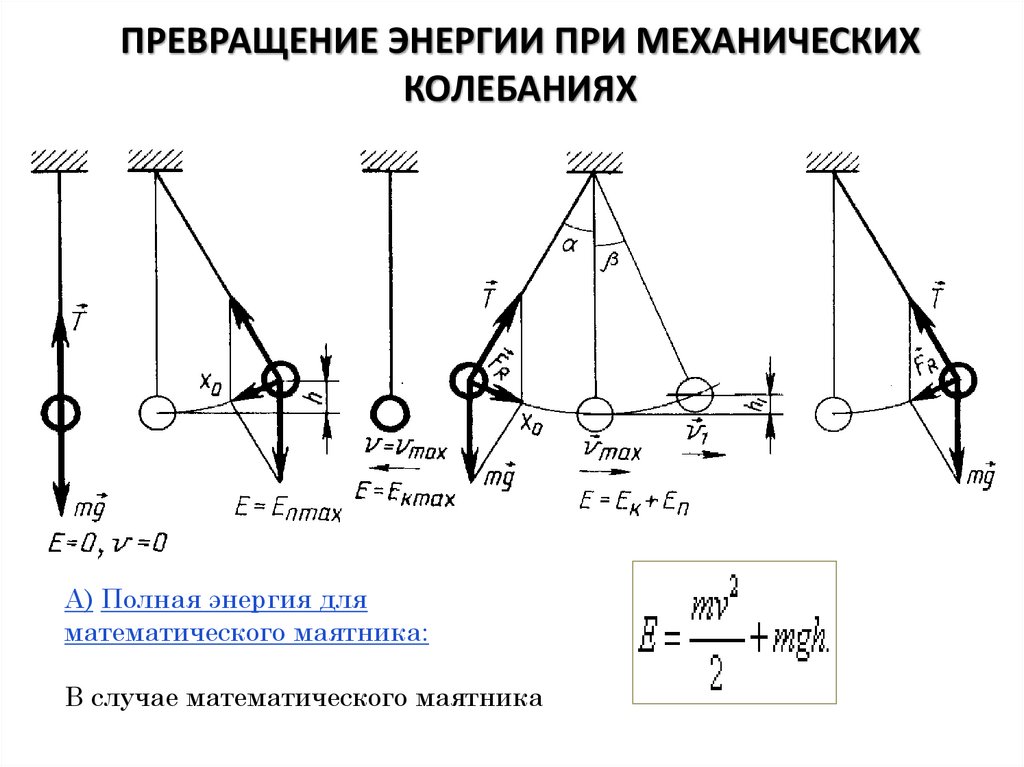
ПРЕВРАЩЕНИЕ ЭНЕРГИИ ПРИ МЕХАНИЧЕСКИХ
КОЛЕБАНИЯХ
А) Полная энергия для
математического маятника:
В случае математического маятника

28.

• Б) Превращения энергии при колебаниях пружинного
маятника происходи в соответствии с законом сохранения
механической энергии:
• При движении маятника вниз или вверх от положения
равновесия его потенциальная энергия увеличивается, а
кинетическая - уменьшается. Когда маятник проходит
положение равновесия (х = 0), его потенциальная энергия
равна нулю и кинетическая энергия маятника имеет
наибольшее значение, равное его полной энергии.
• Таким образом, в процессе свободных колебаний маятника
его потенциальная энергия превращается в кинетическую,
кинетическая в потенциальную, потенциальная затем снова
в кинетическую и т. д. Но полная механическая энергия при
этом остается неизменной.
• Полная энергия пружинного маятника:

29.

• В) При гармонических колебаниях пружинного маятника
происходят превращения потенциальной энергии упруго
деформированного тела:
в его кинетическую энергию:
• где k – коэффициент упругости, х - модуль смещения маятника
из положения равновесия, m - масса маятника, v - его
скорость.
• В соответствии с уравнением гармонических колебаний:

30.

31.

Практическая работа
в группах

32.

Фамилия, имя:_______
,класс:__
«Самоконтроль»:
– многое понял, многому научился;
– я удовлетворен своей работой на
уроке;
– как мало я знаю, мне надо многому
научиться.

33.

Домашнее задание:
Сообщение по теме «Маятники в быту в
природе и в технике» или изготовить любой
маятник