Similar presentations:
Young’s experiment (lecture 5)
1.
Physics 2Voronkov Vladimir Vasilyevich
2. Lecture 5
• Interference– Young’s experiment
• Diffraction
– Fraunhofer Diffraction Pattern
– Intensity of Single-Slit Diffraction Pattern
– Resolution of Slit
– Resolution of Circular Aperture
– Diffraction Grating
3. Physical optics
Ray optics or geometry optics can not explain suchphenomena like polarization, diffraction and
interference. Those are explained by physical
optics or wave optics.
4. Interference
• Interference is spatial superposition of two ormore light waves, which gives increase or decrease
in the amplitude of the resultant wave at different
points of the space.
• Interference at given point is constructive, if the
source waves are in one phase, and the resultant
amplitude is larger then the source amplitudes.
• Interference is destructive, if the source waves are
out of phase, and they cancel each other.
5.
In order to observe interference in light waves, thefollowing conditions must be met:
• The sources must be coherent—that is, they
must maintain a constant phase with respect to
each other.
• The sources should be monochromatic—that is, of
a single wavelength.
• The waves must be of the same polarization.
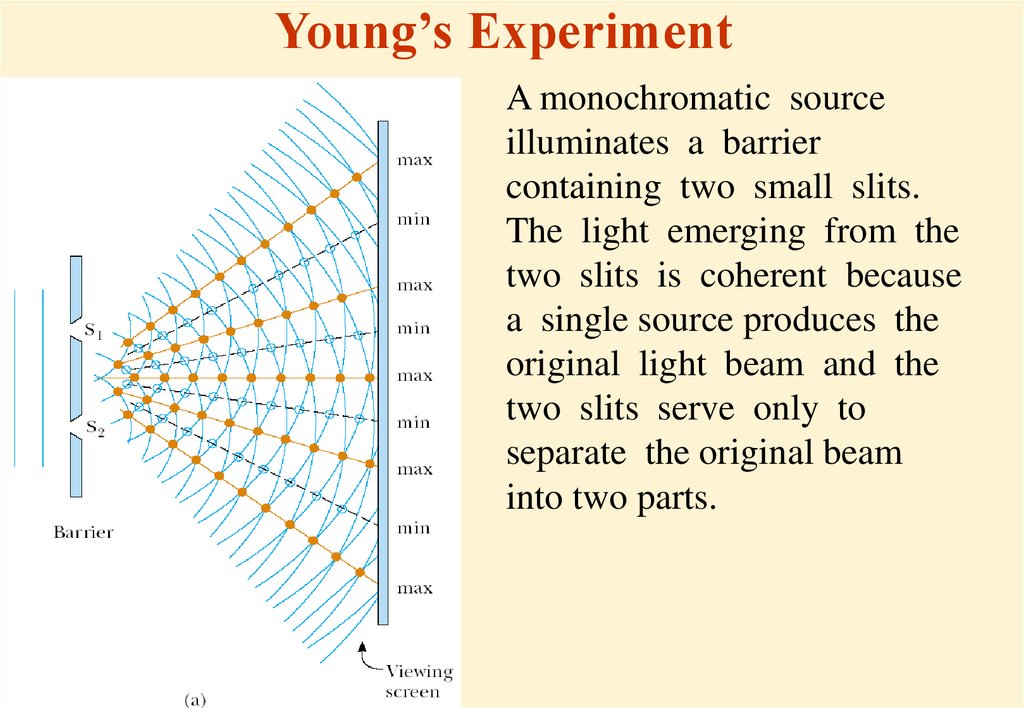
6. Young’s Experiment
A monochromatic sourceilluminates a barrier
containing two small slits.
The light emerging from the
two slits is coherent because
a single source produces the
original light beam and the
two slits serve only to
separate the original beam
into two parts.
7.
• The light from both slitsproduces on a viewing
screen a visible pattern of
bright and dark parallel bands
called fringes.
• When the light from the slits
arrives at a point on the
screen such that
constructive interference
occurs at that location, a
bright fringe appears.
• When the light from the two
slits combines destructively
at any location on the
screen, a dark fringe
results.
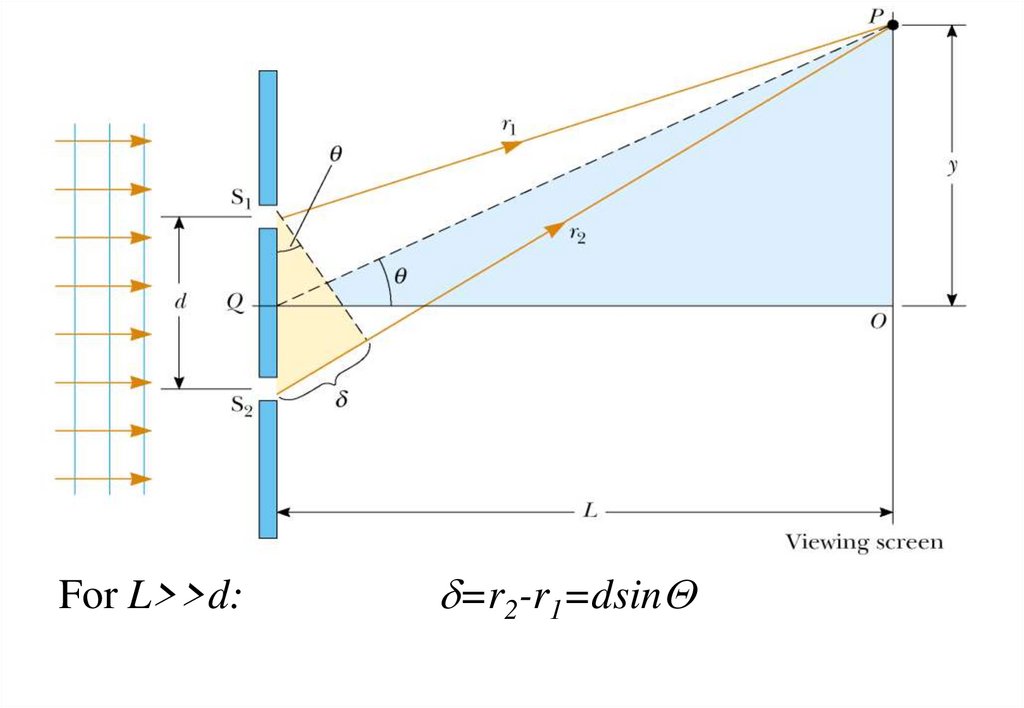
8.
For L>>d:d=r2-r1=dsinQ
9.
Thus, constructive interference is atWhen d is an odd multiple of l/2, the two waves
arriving at point P are 180° out of phase and give
rise to destructive interference. Therefore, the
condition for dark fringes, or destructive
interference, at point P is
10.
To calculate vertical positions of fringes we usethat d>>l because in practice L is often on the
order of 1 m, d a fraction of a millimeter, and ,l a
fraction of a micrometer for visible light. Under
these conditions, Q is small; thus, we can use the
small angle approximation sinQ ≈ tanQ. Then
11.
• Young’s double-slit experiment provides amethod for measuring the wavelength of light. In
fact, Young used this technique to do just that.
• Additionally, Young’s experiment confirms the
wave model of light. It was inconceivable that
particles of light coming through the slits could
cancel each other in a way that would explain the
dark fringes.
12. Diffraction
Term diffraction includes the following phenomena:• Bending of waves around obstacles.
• Interference between waves that emanate from a large
number, or even a continuous set of sources.
• Diffraction gratings consisting of many slits or sources
of coherent light, and such gratings have important
applications in the study of atomic systems and
crystalline materials.
• Behavior of waves after they pass through an aperture;
each infinitesimal part of the aperture acts as a source of
waves, and the resulting pattern of light and dark is a
result of interference among the waves emanating from
these sources.
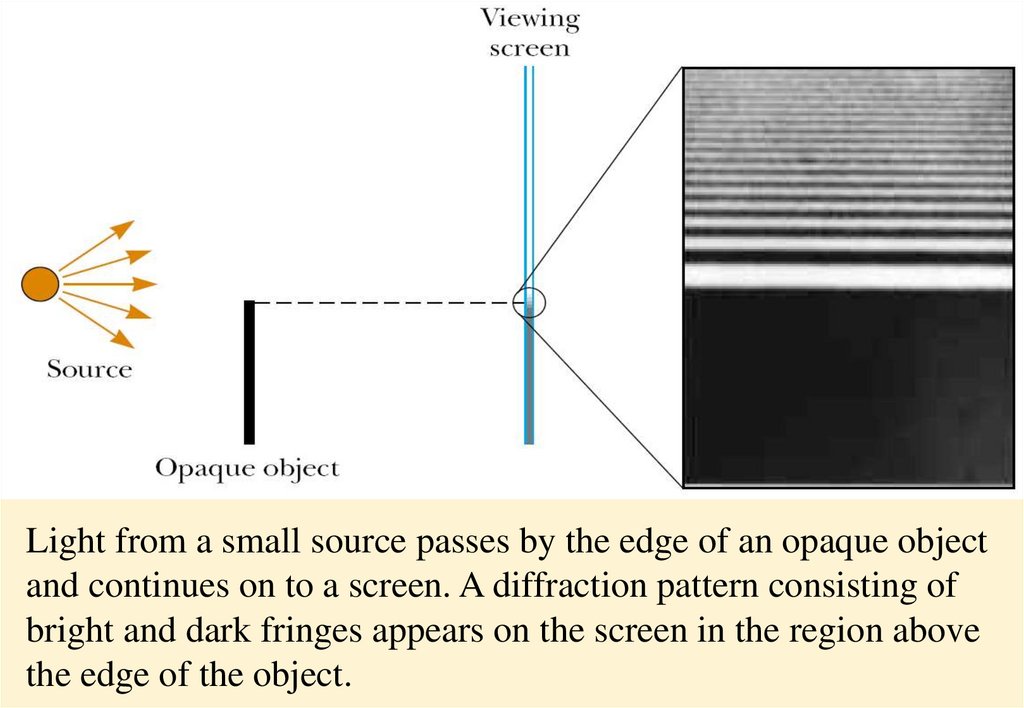
13.
Light from a small source passes by the edge of an opaque objectand continues on to a screen. A diffraction pattern consisting of
bright and dark fringes appears on the screen in the region above
the edge of the object.
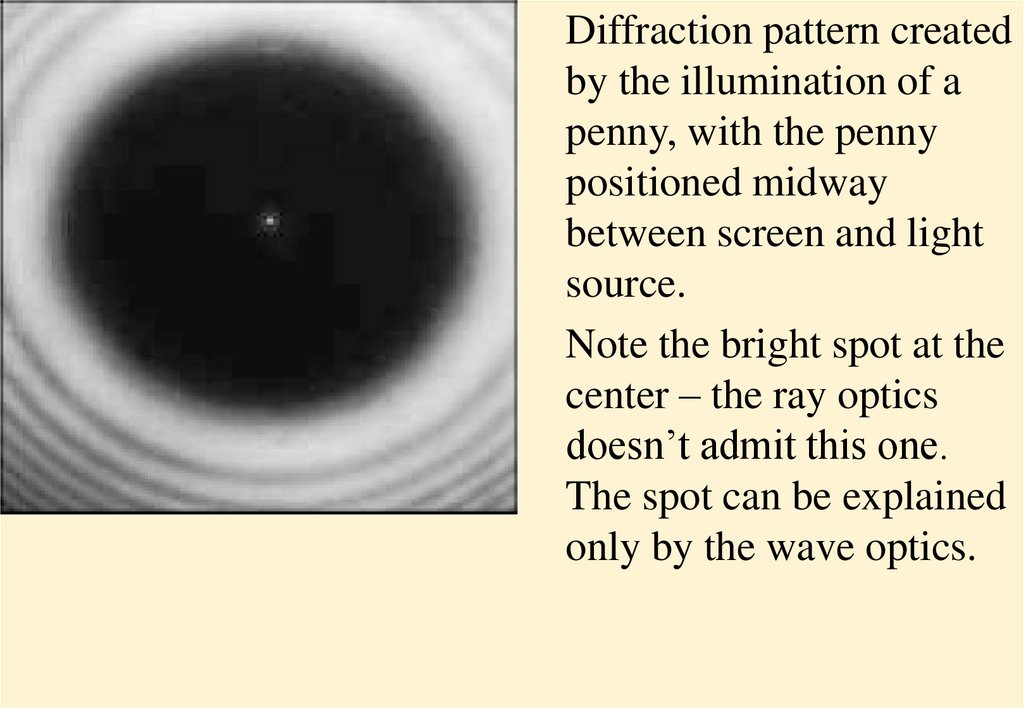
14.
Diffraction pattern createdby the illumination of a
penny, with the penny
positioned midway
between screen and light
source.
Note the bright spot at the
center – the ray optics
doesn’t admit this one.
The spot can be explained
only by the wave optics.
15.
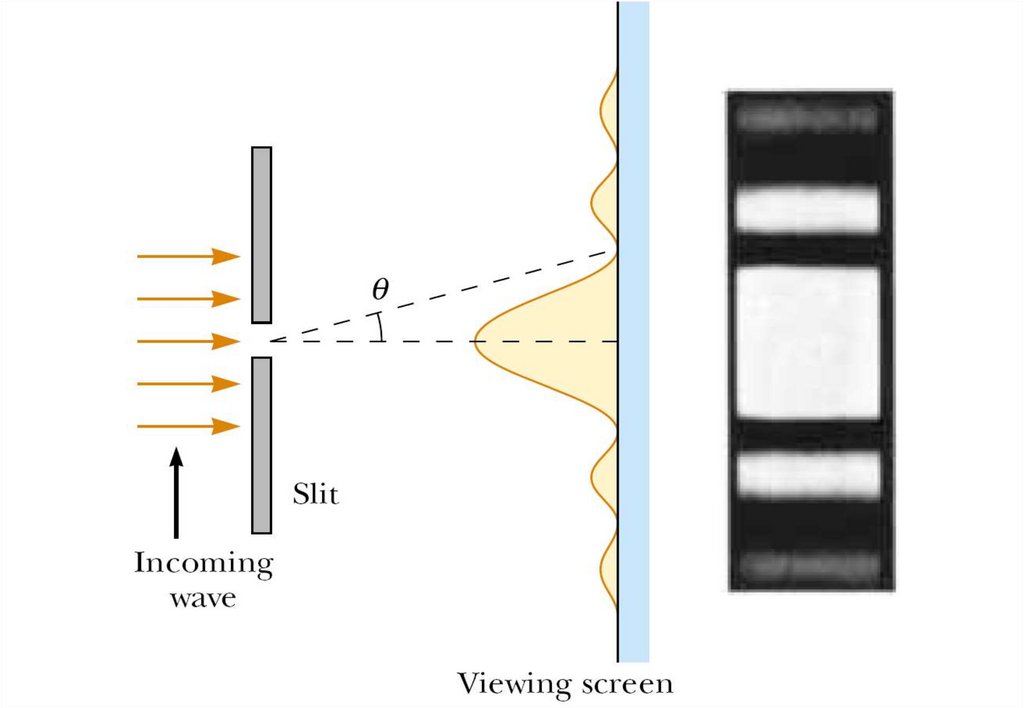
The diffraction pattern thatappears on a screen when
light passes through a narrow
vertical slit. The pattern
consists of a broad central
fringe and a series of less
intense and narrower side
fringes.
16. Fraunhofer Diffraction Pattern
The main assumptions for the Fraunhofer pattern:• The incident waves are planar, for example from a
very distant point source. So, the rays reaching the
screen are approximately parallel.
• The source, aperture, and detector are all very far
apart or when lenses are used to convert spherical
waves into plane waves.
• These assumptions simplify the calculations of
path-length difference and phase differences.
17.
18.
On the previous slide there is Fraunhoferdiffraction pattern of a single slit. The pattern
consists of a central bright fringe flanked by
much weaker maxima alternating with dark
fringes. (Drawing not to scale.). A
photograph of a single-slit Fraunhofer
diffraction pattern is included.
19.
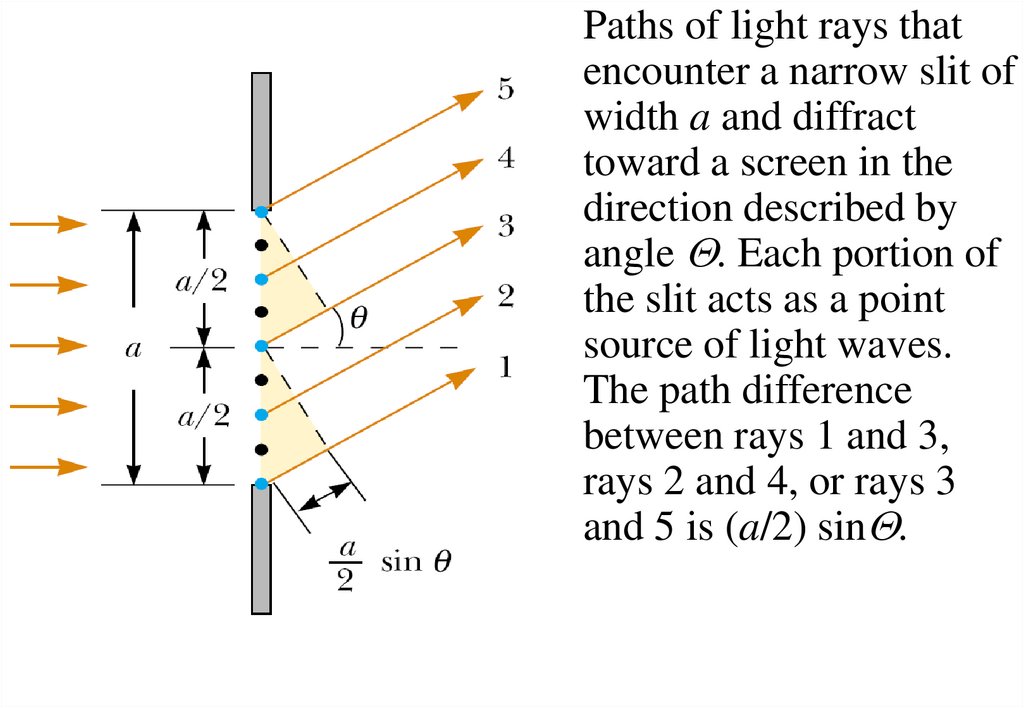
Paths of light rays thatencounter a narrow slit of
width a and diffract
toward a screen in the
direction described by
angle Q. Each portion of
the slit acts as a point
source of light waves.
The path difference
between rays 1 and 3,
rays 2 and 4, or rays 3
and 5 is (a/2) sinQ.
20.
According to Huygens’s principle, each portion ofthe slit acts as a source of light waves. Hence, light
from one portion of the slit can interfere with light
from another portion, and the resultant light
intensity on a viewing screen depends on the
direction Q. Based on this analysis, we recognize
that a diffraction pattern is actually an interference
pattern, in which the different sources of light are
different portions of the single slit.
21.
Considering that all the waves are in phase as they leave theslit, we can state that ray 1 travels farther than ray 3 by an
amount equal to the path difference (a/2)sinQ, where a is the
width of the slit. Similarly, the path difference between rays 2
and 4 is also (a/2) sinQ, as is that between rays 3 and 5. If this
path difference is exactly half a wavelength (corresponding to a
phase difference of 180°), then the two waves cancel each
other and destructive interference results. If this is true for two
such rays, then it is true for any two rays that originate at
points separated by half the slit width because the phase
difference between two such points is 180°. Therefore, waves
from the upper half of the slit interfere destructively with
waves from the lower half when
22.
Thus, we have destructive interference whenThis result was obtained when we divided the slit
into two equal parts. If we divide the slit into even
number parts 2m, then we get the condition for
destructive interference:
23.
A broad central bright fringe is observed; this fringe is flanked bymuch weaker bright fringes alternating with dark fringes. The various
dark fringes occur at the values of Qdark. Each bright-fringe peak
lies approximately halfway between its bordering dark-fringe minima.
Note that the central bright maximum is twice as wide as the
secondary maxima.
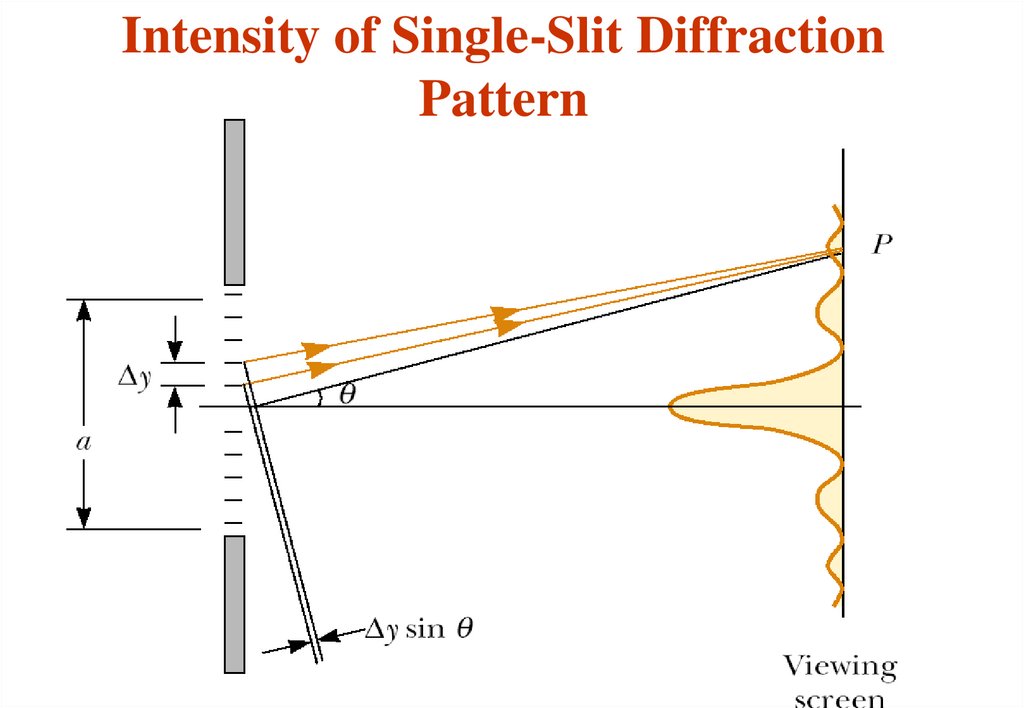
24. Intensity of Single-Slit Diffraction Pattern
25.
Each zone Dy acts as a source of coherentradiation, and each contributes an incremental
electric eld of magnitude E at some point on the
screen. We obtain the total electric eld
magnitude E at a point on the screen by
summing the contributions from all the zones.
The incremental electric eld magnitudes between
adjacent zones are out of phase with one another
by an amount Db:
26.
To nd the magnitude of the total electric eld on thescreen at any angle Q, we sum the incremental
magnitudes DE due to each zone. For small values of Q,
we can assume that all the DE values are the same. It is
convenient to use phasor diagrams for various angles.
When Q = 0, all phasors are aligned, because all the waves
from the various zones are in phase:
In this case, the total electric eld at the center of the
screen is E0=NDE, where N is the number of zones.
27.
The resultant magnitude ER at some small angle Q. Each phasordiffers in phase from an adjacent one by an amount Db. In this
case, ER is the vector sum of the incremental magnitudes and
hence is given by the length of the chord. Therefore, ER < E0.
The total phase difference b between waves from the top and
bottom portions of the slit is
where a=NDy is the width of the slit.
28.
As Q increases, the chain of phasors eventually forms theclosed path:
At this point, the vector sum is zero, and so ER = 0,
corresponding to the rst minimum on the screen. Noting that b
= NDb = 2p in this situation, we see from the equation in the
previous slide that:
This equation for the first minimum is in agreement with the one
we received using only the Huygens’s principle.
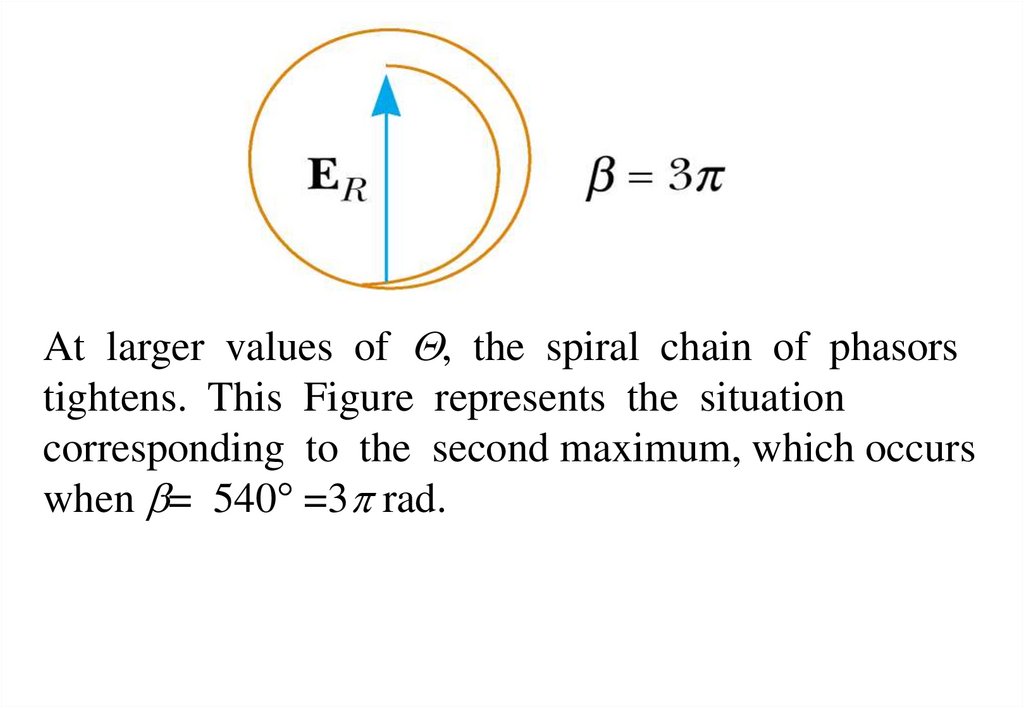
29.
At larger values of Q, the spiral chain of phasorstightens. This Figure represents the situation
corresponding to the second maximum, which occurs
when b= 540° =3p rad.
30.
All the ends of the phasorslie on the circular arc of
radius R. The resultant
electric field magnitude ER
equals the length of the
chord (blue line).
Combining with the
previous expression:
31.
The resultant light intensity I at a point on the screen isproportional to the square of the magnitude ER:
I ~ E2R
Then we get the expression for intensity:
where Imax is the intensity at Q = 0 (the central maximum).
Substituting the expression for b we obtain:
32.
From the obtained result minima occur whenor
The result is in agreement with the previous
expression obtained using only the Huygens's
principle.
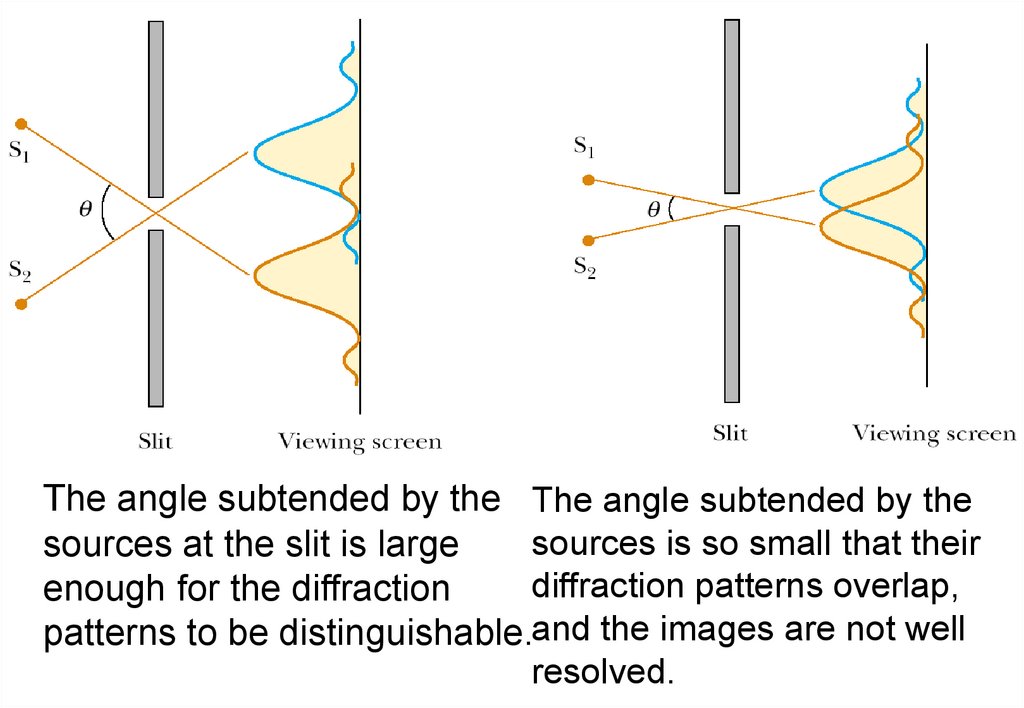
33. Resolution of Slit
• If the two sources are far enough apart to keep theircentral maxima from overlapping, their images can be
distinguished and are said to be resolved.
• If the sources are close together, the two central maxima
overlap, and the images are not resolved.
Rayleigh’s criterion is used to determine whether two
images are resolved:
When the central maximum of one image falls on
the rst minimum of another image, the images are
said to be just resolved.
34.
The angle subtended by the The angle subtended by thesources is so small that their
sources at the slit is large
diffraction patterns overlap,
enough for the diffraction
patterns to be distinguishable.and the images are not well
resolved.
35.
From Rayleigh’s criterion, we can determine the minimumangular separation Qmin subtended by the sources at the slit
for which the images are just resolved. Using the equation
for the minima in a single-slit diffraction, we can define the
angle of the first minimum as
Considering that l<<a:
For the images to be resolved, the angle subtended by the two
sources at the slit must be greater than l/a.
36. Resolution of Circular Aperture
The sources arefar apart, and the
patterns are well
resolved.
The sources are closer
The sources are so
together such that the
close together that
angular separation just
the patterns are
satis es Rayleigh’s
not resolved.
criterion, and the patterns
are just resolved.
37.
Mathematical analysis shows that the limitingangle of resolution of the circular aperture is
D is the diameter of the aperture,
l is the wavelength of the incident light.
Note that this expression is like that for slit.
38. Diffraction Grating
The diffraction grating, consists of a large number of equallyspaced parallel slits.
• A transmission grating can be made by cutting parallel
grooves on a glass plate with a precision ruling machine. The
spaces between the grooves are transparent to the light and
hence act as separate slits.
• A re ection grating can be made by cutting parallel grooves
on the surface of a re ective material. The re ection of light
from the spaces between the grooves is specular, and
the re ection from the grooves cut into the material is
diffuse.
• Current technology can produce gratings with slit spacing d =
(1/5 000) cm = 2*10-4 cm.
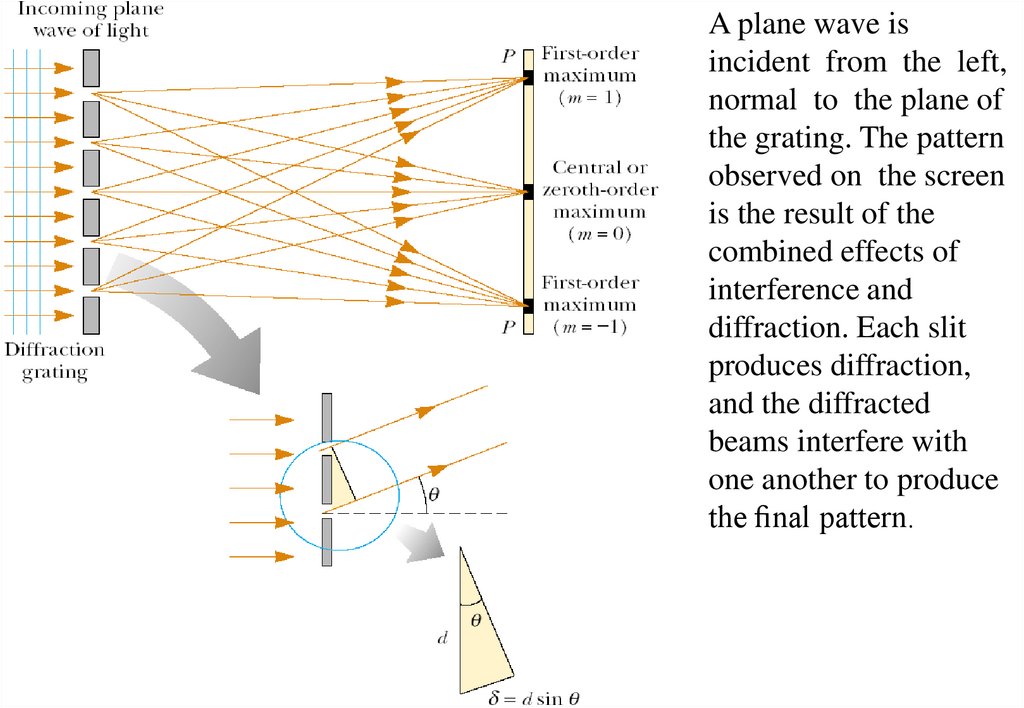
39.
A plane wave isincident from the left,
normal to the plane of
the grating. The pattern
observed on the screen
is the result of the
combined effects of
interference and
diffraction. Each slit
produces diffraction,
and the diffracted
beams interfere with
one another to produce
the nal pattern.
40.
The waves from all slits are in phase as they leave theslits. However, for some arbitrary direction Q measured
from the horizontal, the waves must travel different path
lengths before reaching the screen. The path difference d
between rays from any two adjacent slits is equal to
d sin Q. If this path difference equals one wavelength or
some integral multiple of a wavelength, then waves from
all slits are in phase at the screen and a bright fringe is
observed. Therefore, the condition for maxima in the
interference pattern at the angle Qbright is
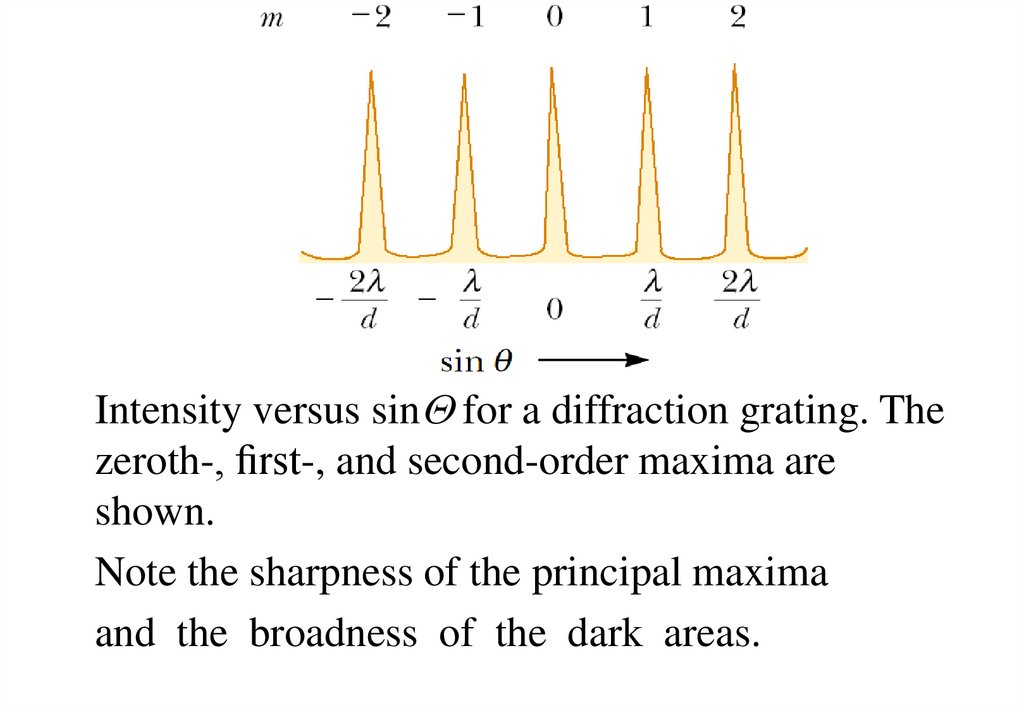
41.
Intensity versus sinQ for a diffraction grating. Thezeroth-, rst-, and second-order maxima are
shown.
Note the sharpness of the principal maxima
and the broadness of the dark areas.






























 physics
physics








