39-Презентация-А-9

1.

Числовые
неравенства и их
свойства

2.

Определение
Действительное число а больше (меньше)
действительного числа b, если их разность
(а-b)- положительное (отрицательное)
число.
Пишут: а > в ( а < в )
Такие неравенства называются строгими.

3.

Строгие неравенства
• а > 0 означает, что а– положительное число
• а < 0 означает, что а – отрицательное число
• а > b означает, что (а-b)-положительное
число, т.е. (а-b)>0
• а < b означает, что (а-b)- отрицательное
число, т.е. (а-b)<0

4.

Нестрогие неравенства
• а ≥ 0 означает, что а больше нуля или
равно нулю, т.е. а – неотрицательное число,
или что а не меньше нуля
• а ≤ 0 означает, что а меньше нуля или
равно нулю, т.е. а – неположительное число,
или что а не больше нуля

5.

Нестрогие неравенства
• а ≥ b означает, что а больше b или равно
b, т.е. а-b – неотрицательное число, или
что а не меньше b; а-b ≥ 0
• а ≤ b означает, что а меньше в или равно
b, т.е. а-b – неположительное число, или
что а не больше b; а-в ≤ 0

6.

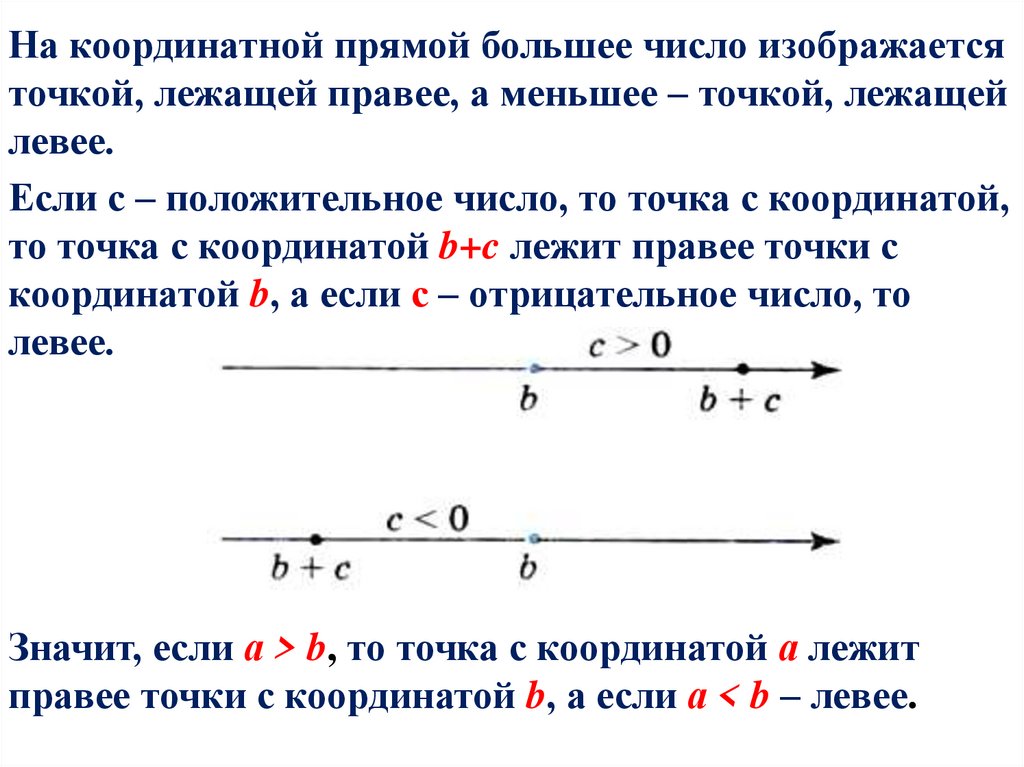
На координатной прямой большее число изображается
точкой, лежащей правее, а меньшее – точкой, лежащей
левее.
Если с – положительное число, то точка с координатой,
то точка с координатой b+c лежит правее точки с
координатой b, а если с – отрицательное число, то
левее.
Значит, если а > b, то точка с координатой а лежит
правее точки с координатой b, а если а < b – левее.

7.

Докажите, что при любых значениях a верно
неравенство
Решение

8.

Доказать, что при любых значениях переменной а
верно неравенство:

9.

Свойства числовых неравенств
Свойства:
1) если а>b, b>с, то а>с
Например:
1) если 5>3, 3>-4, то 5>-4
2) если а>b, то а+с >b+с
2) если 5>3, то 5+2 >3+2
3) если а>b и m>0, то
аm>bm
3) если 5>3 и 10>0, то
5·10>3·10, т.е. 50>30
4) если а>b и m<0, то
аm<bm
4) если 5>3 и -2<0, то
5·(-2)< 3·(-1), т.е. -10<-3
5) если а>b, то -а<-b
5) если 5>3, то -5<-3

10.

Свойства числовых неравенств
6) если а>b, с>d, то
а+с>b+d
6) если 5>3, 4>2, то
5 + 4 > 3 + 2, т.е. 9>5
7) если а>b>0 и с>d >0,
то ас > bd
7) если 5>3>0 и 4>2 >0,
то 5·4 > 3·2, т.е. 20>6
8) если а>b≥0, nєN,
то аⁿ > bⁿ
8) если 5>3≥0, 2єN,
то 5² > 3², т.е. 25 > 9
9) если а>b>0, то
1/а < 1/b
9) если 5>3>0, то 1/5<1/3

11.

Пример 3: Известно, что 2,1 < а < 2,2; 3,7 < b < 3,8. Найти
оценки для числа: а ) 2а; б ) 3b; в ) a b; г ) a b; д) а 2 ;
1
3
е) b ; ж ) ;
a
а ) 2 а;
2,1 а 2, 2; 2
3, 7 b 3,8; (-1)
3 3,7 3b 3 3,8;
2 2,1 2а 2 2, 2;
4, 2 2а 4, 4.
11, 4 3b 11,1;
в ) a b;
2,1 а 2, 2
+
3, 7 b 3, 8
5,8 a b 6,0.
д) а 2 ;
2,12 а 2 2, 22 ;
4, 41 а 2 4,84.
г ) a b;
3, 7 b 3,8; (-1)
3,7 b 3,8;
3,8 b 3,7;
2,1 а 2, 2
+
3,8 b 3,7
1, 7 а b 1,5.

12.

Пример 3: Известно, что 2,1 < а < 2,2; 3,7 < b < 3,8. Найти
оценки для числа:
е) b 3 ;
3, 7 b 3,8;
3, 73 b3 3,83 ;
50, 653 b3 54,872.
1
ж) ;
a
a b;
1 1
;
a b
2,1 а 2, 2;
1
1
1
;
2,1 a 2, 2
5 1 10
.
11 a 21

13.

Пример 5: Сравнить числа:
a)
Решение:
a) 3 6 и 2 5;
б ) 10 и 4 11;
a 3 6;
3 6 и 2 5;
b 2 5;
3 6 3 2 3 6 6 3 2 18 6 9 72;
b 2 5 4 4 5 5 9 80.
2
a
2
2
2
72 80;
9 72 9 80;
a 2 b2 ;
a b.
б ) 10 и 4 11;
4;
10 11;
10 4 11.
2
2