Similar presentations:
Элементы комбинаторики и их применение для нахождения вероятности событий
1.
Мишень настроения!Классная работа.
ДАТА
2.
Элементы комбинаторики и ихприменение для нахождения
вероятности событий.
Цель урока:
Учащийся:
- различает понятия: «перестановки», «размещения» и «сочетания» без
повторений и с повторениями;
- умеет решать задачи с применением формулы для вычисления
перестановок, сочетаний, размещений без повторений;
- умеет решать задачи с применением формулы для вычисления
перестановок, сочетаний, размещений с повторениями.
Критерии оценивания:
Обучающийся:
- решает задачи, используя формулы для вычисления перестановок,
сочетаний, размещений без повторений;
- применяет формулы для вычисления перестановок, сочетаний,
размещений с повторениями при решении задач.
3.
Изучи или вспомни!Основные формулы комбинаторики
4.
Перестановками называют комбинации, состоящие из одних итех же n различных объектов и отличающиеся только
порядком их расположения.
Отличительной особенностью перестановок является то, что в
каждой из них участвует ВСЁ множество, то есть, все
n
объектов.
Перестановки с повторениями
n!
Pn (n1; n2 ;...nk )
n1! n2! ... nk !
Пример
Сколько различных слов
можно получить
переставляя буквы слова
«МАМА»
5.
ПримерыСловом будем называть любую конечную последовательность
букв. Необходимо выяснить, сколько различных слов можно
получить, переставляя буквы того или иного слова:
1) «ВЕКТОР»
2) «ЛИНИЯ»
3) «ПАРАБОЛА»
4) «БИССЕКТРИСА»
5) «МАТЕМАТИКА»
6.
ПримерыСловом будем называть любую конечную последовательность
букв. Необходимо выяснить, сколько различных слов можно
получить, переставляя буквы того или иного слова:
= 6! (все буквы различны)
1) «ВЕКТОР»
2) «ЛИНИЯ»
= 5!/2! = 60 (есть две одинаковые буквы И)
3) «ПАРАБОЛА»
= 8!/3!
4) «БИССЕКТРИСА»
= 11! / (2!∙3!)
5) «МАТЕМАТИКА»
=10! / (3!∙2!∙2!)
7.
Размещенияминазывают различные комбинации из m объектов, которые
выбраны из множества n различных объектов, и которые
отличаются друг от друга как составом объектов в выборке, так
и их порядком.
Размещения с повторениями
A n
m
n
m
Пример
Сколько различных чисел может
быть на экране калькулятора,
имеющего 5 регистров?
8.
Примеры1. Даны цифры 1;2;3;4. Сколько различных двузначных
чисел можно составить, если цифры в числе могут
повторяться?
2. Для создания 3-значного пароля используются символы
из алфавита {+,*,A,!,2}.
Сколько всего паролей можно составить?
9.
Примеры1. Даны цифры 1;2;3;4. Сколько различных двузначных чисел можно
составить, если цифры в числе могут повторяться?
Решение
так как цифры в числе могут повторяться, нужно использовать формулу числа
размещений с повторениями из n элементов по k, где n=4 (множество всех
элементов), k=2 (т. к. нужно составить двузначные числа).
A42 42 16
2. Для создания 3-значного пароля используются символы из алфавита
{+,*,A,!,2}.
Сколько всего паролей можно составить?
Решение
По условию n=5, k=3. Рассматриваем размещение 5 символов по 3 позициям с
повторениями:
A53 53 125
10.
Сочетанияминазывают различные комбинации из m объектов, которые
выбраны из множества n различных объектов, и которые
отличаются друг от друга хотя бы одним объектом.
Иными словами, отдельно взятое сочетание – это уникальная
выборка из m
элементов, в которой не важен их
порядок (расположение)
Сочетания с повторениями
n 1
n m 1
C C
m
n
(n m 1)!
m! (n 1)!
Пример
В кондитерской имеется 7 видов
пирожных. Сколько различных
наборов по 4 пирожных можно
составить при том, что пирожные
могут быть в наборе одинаковыми?
11.
Примеры1. В магазине продаются булочки трех видов: с маком, изюмом и повидлом.
Мама послала Колю купить 6 булочек. Сколько возможных вариантов выбора у
него есть?
2. Сколько решений в неотрицательных числах имеет уравнение x+y+z+q=8?
12.
Примеры1. В магазине продаются булочки трех видов: с маком, изюмом и повидлом.
Мама послала Колю купить 6 булочек. Сколько возможных вариантов выбора у
него есть?
Решение. По условию задачи требуется составить комбинацию из k=6 элементов,
которые выбираются (возможны повторения) из объектов n=3типов (с маком,
изюмом, или повидлом). Всего возможных наборов булочек будет (по формуле
сочетаний с повторениями):
3 1
3 6 1
C C
6
3
8! 7 8
C
28
6!2!
2
2
8
2. Сколько решений в неотрицательных числах имеет уравнение x+y+z+q=8?
Решение. Переформулируем задачу в терминах шаров и ящиков. Пусть у нас
есть k=8 шаров/единичек, их нужно разместить в n=4 ящиках (каждый ящик это слагаемое в выражении слева, вместе как раз шаров во всех ящиках будет 8,
то есть равенство выполнится). Так как решение требуется в неотрицательных
числах, то ящик в том числе может быть пустым (дополнительных ограничений
нет). Применяем формулу числа сочетаний с повторениями:
C48 C44 81 1 C113
11! 9 10 11
165
8!3!
2 3
13.
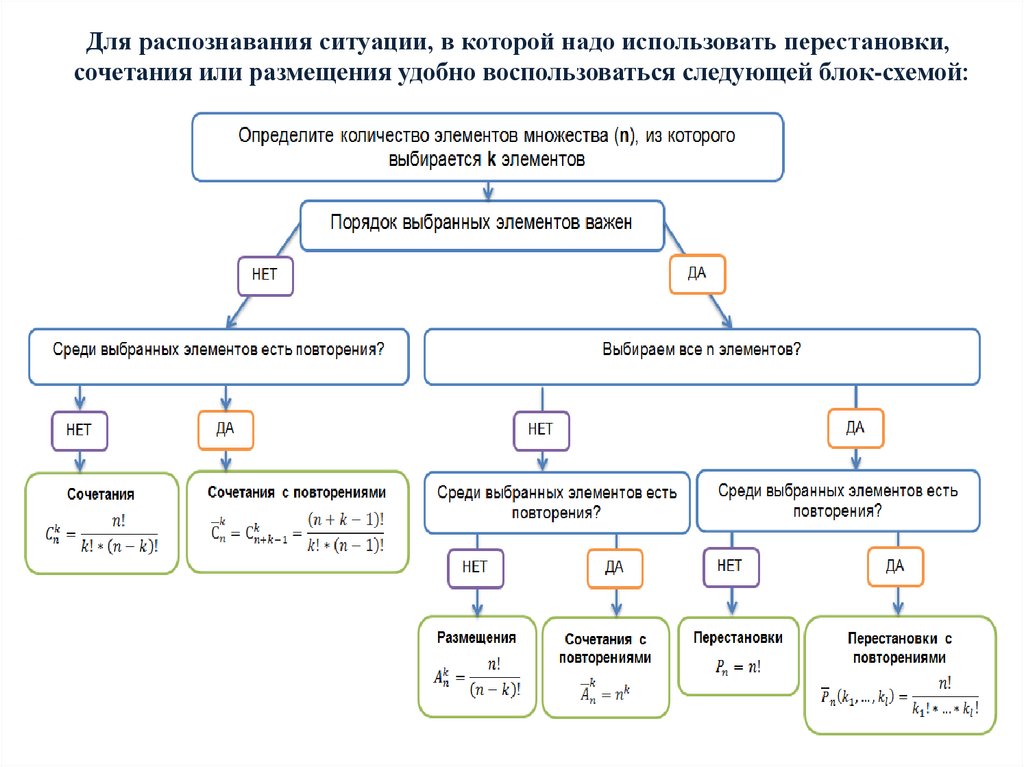
Для распознавания ситуации, в которой надо использовать перестановки,сочетания или размещения удобно воспользоваться следующей блок-схемой:
14.
Теория вероятностей- классическое определение вероятности.
Пример
В среднем на 50 исправных фонариков приходится два
неисправных. Найдите вероятность купить работающий
фонарик. Результат округлите до сотых.
Решение.
Здесь важно не ошибиться.
Если на 50 работающих фонариков с одной стороны
приходится 2 неработающих, то всего фонариков – 52!
Это тонкость этой задачи. Вероятность купить
работающий фонарик равна 50/52, т.е. 0,9615. Округляем до
сотых, получаем 0,96.
Ответ: 0,96.
15.
Выполни в тетради самостоятельно!16.
Выполни в тетради самостоятельно!17.
Домашнее задание!1) Сколькими способами можно собрать
гирлянду из 4 красных, 4 синих и 8 желтых
флажков?
2) В классе из 20 учащихся 4 отличника и 7
хорошистов. Сколькими способами из них
можно отобрать команду на олимпиаду по
математике в 6 человек так, чтобы среди них
было хотя бы два отличника?
18.
Вернемся к цели урока!Цель урока:
Учащийся:
- различает понятия: «перестановки», «размещения» и «сочетания» без
повторений и с повторениями;
- умеет решать задачи с применением формулы для вычисления
перестановок, сочетаний, размещений без повторений;
- умеет решать задачи с применением формулы для вычисления
перестановок, сочетаний, размещений с повторениями.
Что узнал?
Чему научился?
Что осталось непонятным?
Над чем надо поработать?

















 mathematics
mathematics








