Similar presentations:
Комплексные числа
1. Какие числовые множества Вам знакомы?
NZ
Q
R
• N – натуральные числа
• Z – целые числа
• Q – рациональные числа
• R – действительные числа
2. Комплексные числа
- понятие о комплексном числе- арифметические действия над числами
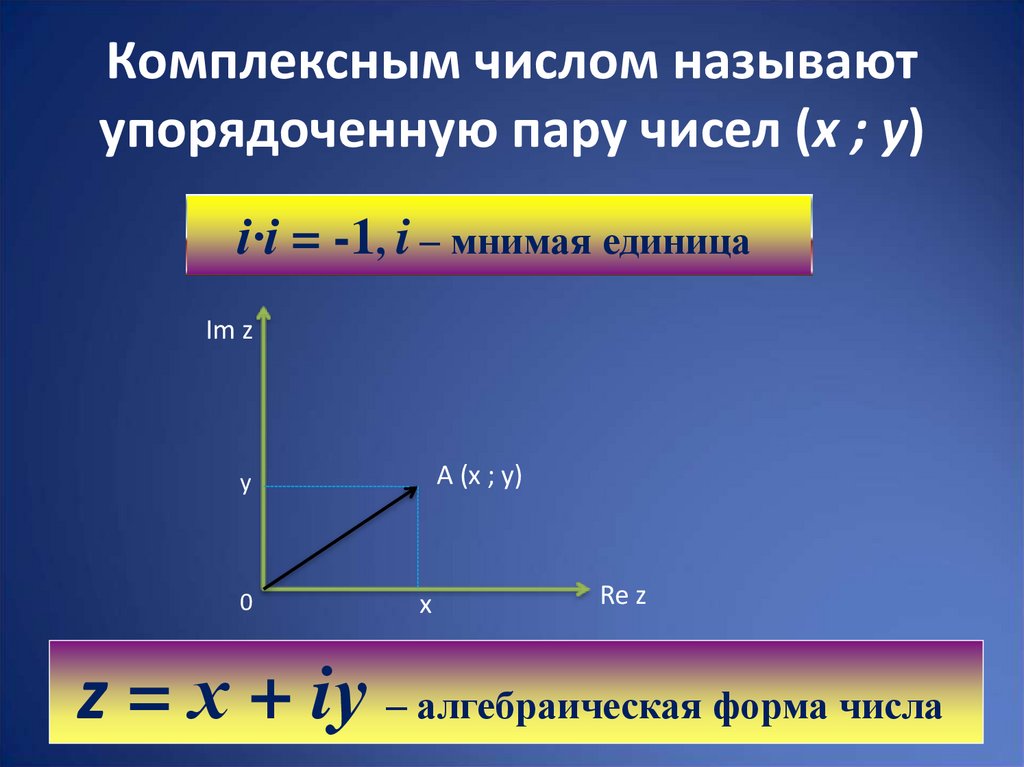
3. Комплексным числом называют упорядоченную пару чисел (х ; у)
i·i = -1, i – мнимая единицаIm z
А (х ; у)
у
0
х
Re z
z = х + iу – алгебраическая форма числа
4. Сопряженные комплексные числа
Если у комплексного числа z сохранить действительнуючасть и поменять знак у мнимой части, то получится
комплексное число, сопряженное данному обозначается z
если z х уi, тоz х уi
Из всех комплексных чисел только действительные числа
равны своим сопряженным числам
5. Тригонометрическая форма комплексного числа
z = r (cosφ + i sinφ)Im z
r
sin
А (х ; у)
0
х у
Re z
cos
2
2
у
2
х у
х
2
х у
2
2
6.
Z =r =А В
cos
A
sin
2
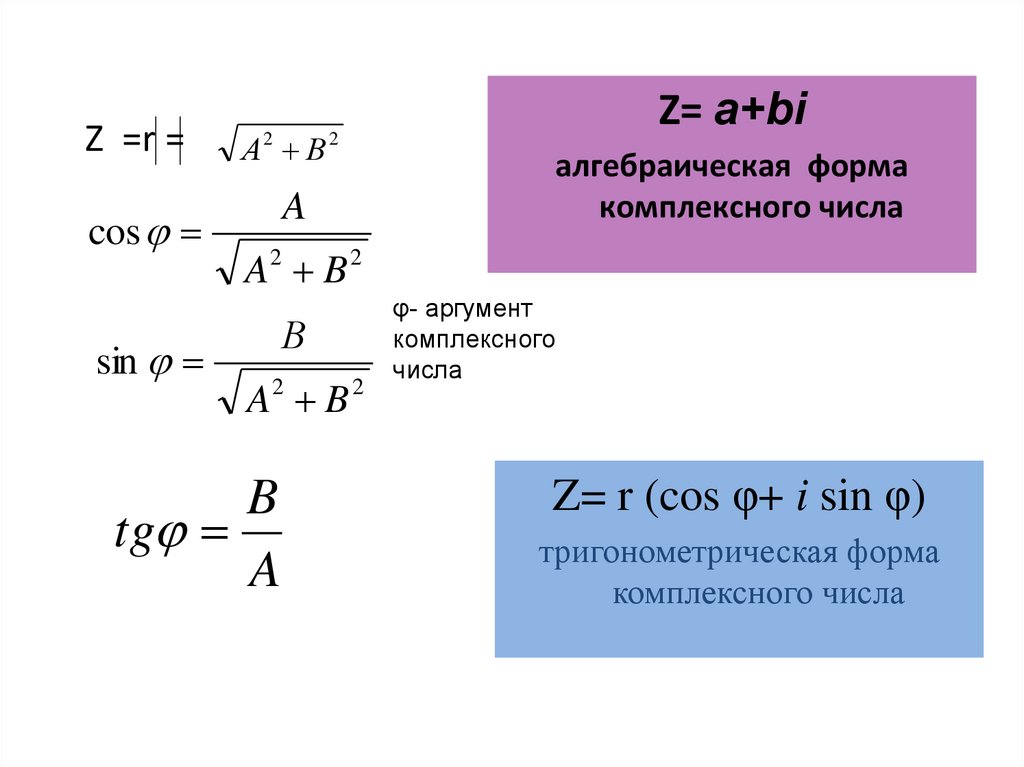
Z= a+bi
2
алгебраическая форма
комплексного числа
A2 B 2
В
A2 B 2
B
tg
A
φ- аргумент
комплексного
числа
Z= r (cos φ+ i sin φ)
тригонометрическая форма
комплексного числа
7.
2 2Требуется записать число z в
1 i
алгебраической и тригонометрической формах;
Решение:
Комплексное число z в алгебраической форме имеет вид: z=а+bi;
в тригонометрической форме: z=r(cos +i sin ), где r a 2 b 2 и
b
arctg .
a
2 2
Для тог чтобы записать z
в алгебраической форме, умножим
1 i
числитель и знаменатель на сопряженное к знаменателю, т. е. на 1- i.
Пример 1:Дано комплексное число z
2 2 1 i 2 2 2 2i 2 2 2 2i
2 2i .
2
1 i 1 i
2
1 i
z 2 2i - алгебраическая форма.
z
a 2 , b 2 , r
2 2 2 2 2 ,
arctg
2
2
2
2
arctg 1
4
3
3
z 2 cos
i sin
- тригонометрическая форма.
4
4
2
3
.
4
8. Задание 1: Дано комплексное число . Требуется записать его в алгебраической и тригонометрической формах
Задание 1. z 4 1 iЗадание 2. z 2 2
3 i
Задание 3. z 1 3 i





 mathematics
mathematics








