Similar presentations:
Логические элементы. Алгебра логики
1. 28.11 Практическая работа. Логические элементы. Алгебра логики
Ход работы.Внимательно изучить материалы презентации.
1. Выполнить задачи к слайдам 4-9 (можно в
электронном варианте. В презентации составить
таблицу истинности или вычислить для заданного
значения переменных)
2. Выписать основные законы логики, пару примеров
с выполнением и выполнить упрощение для
задания слайда 30-32)
Буду ждать ваши работы до 2.12 на адрес
school136@mail.ru
2.
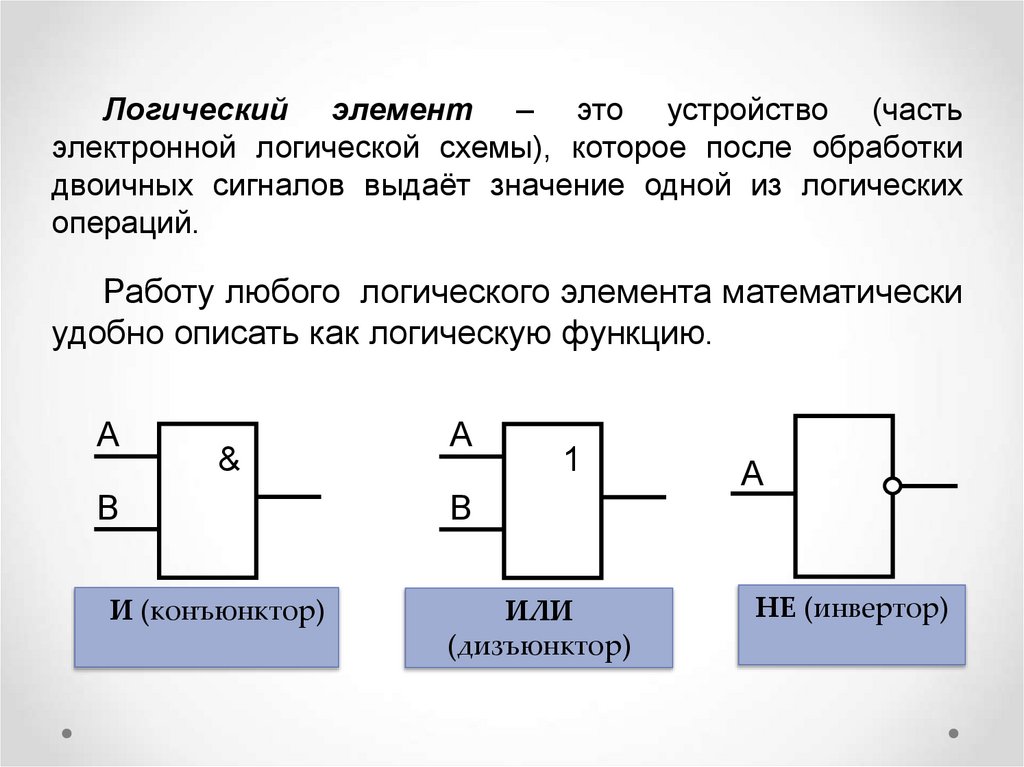
Логический элемент – это устройство (частьэлектронной логической схемы), которое после обработки
двоичных сигналов выдаёт значение одной из логических
операций.
Работу любого логического элемента математически
удобно описать как логическую функцию.
А
&
А
1
В
В
И (конъюнктор)
ИЛИ
(дизъюнктор)
А
НЕ (инвертор)
3.
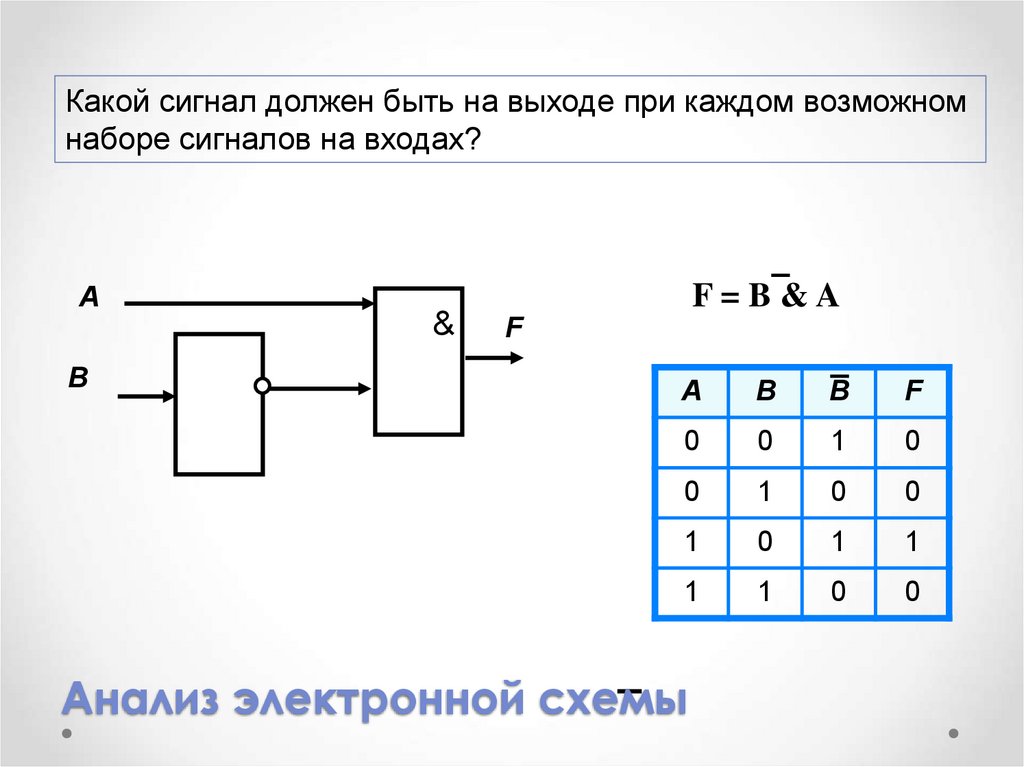
Какой сигнал должен быть на выходе при каждом возможномнаборе сигналов на входах?
А
В
&
F=B&A
F
A
B
B
F
0
0
1
0
0
1
0
0
1
0
1
1
1
1
0
0
Анализ электронной схемы
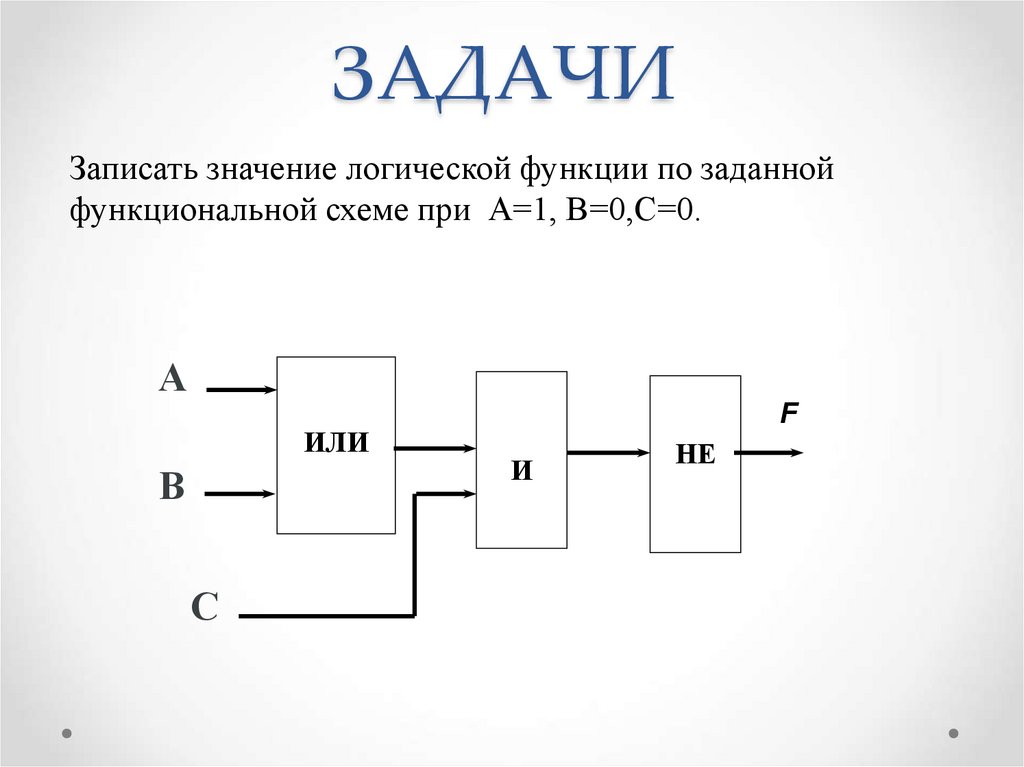
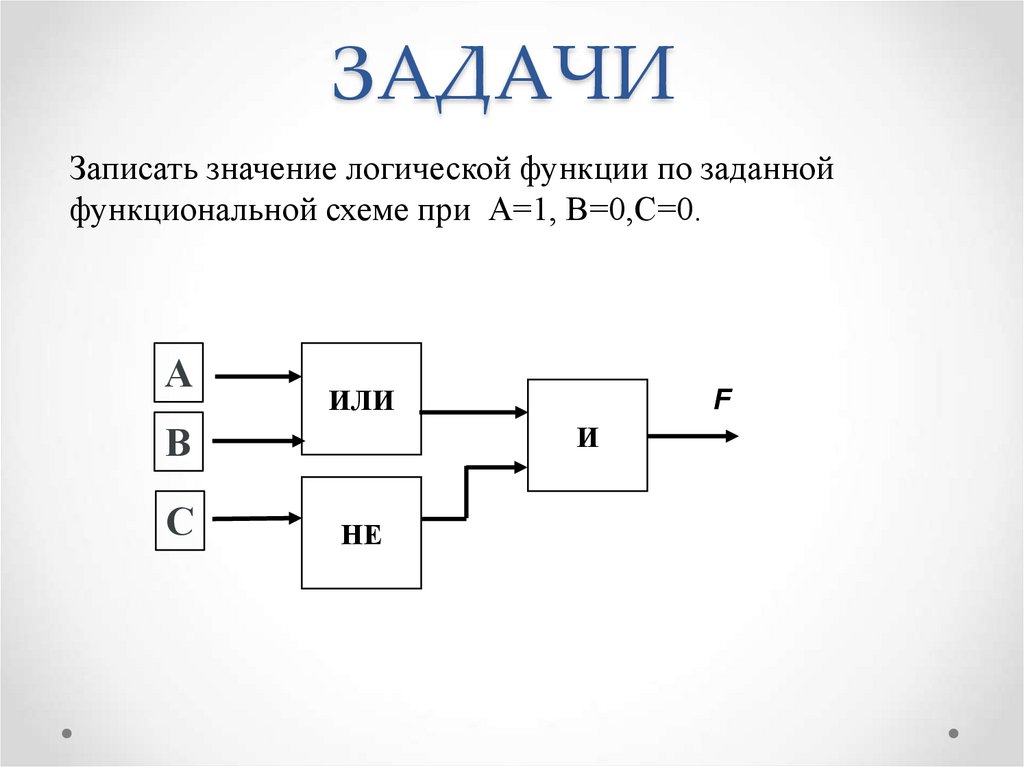
4. ЗАДАЧИ
Записать значение логической функции по заданнойфункциональной схеме при А=1, В=0,С=0.
А
ИЛИ
В
С
F
И
НЕ
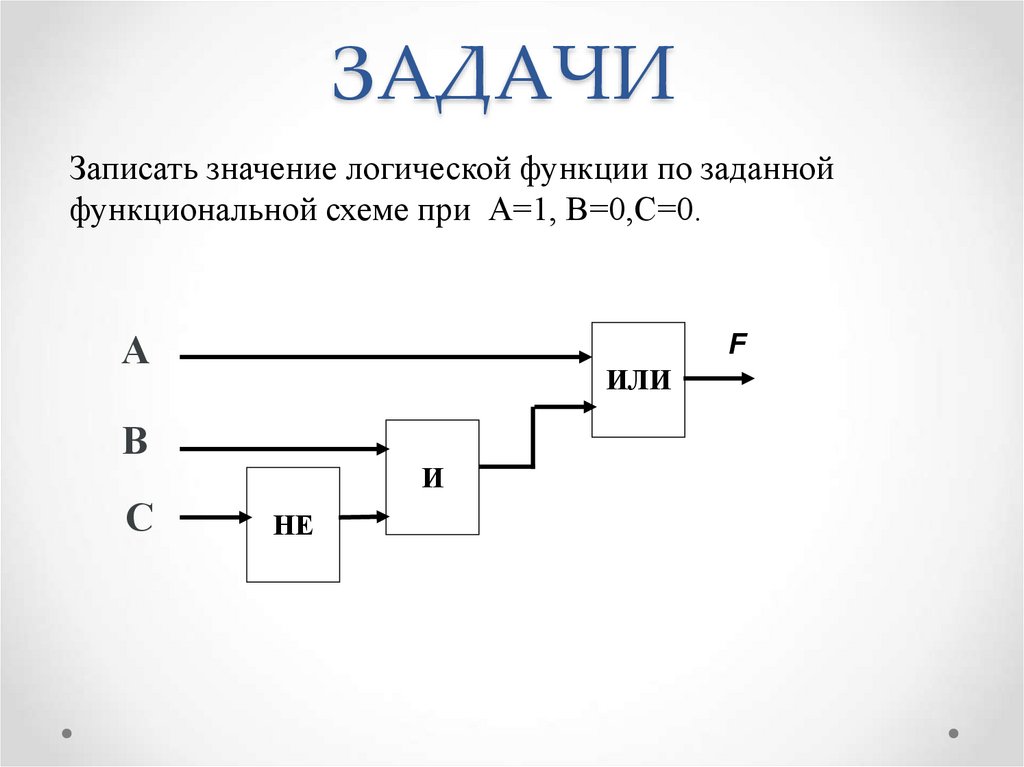
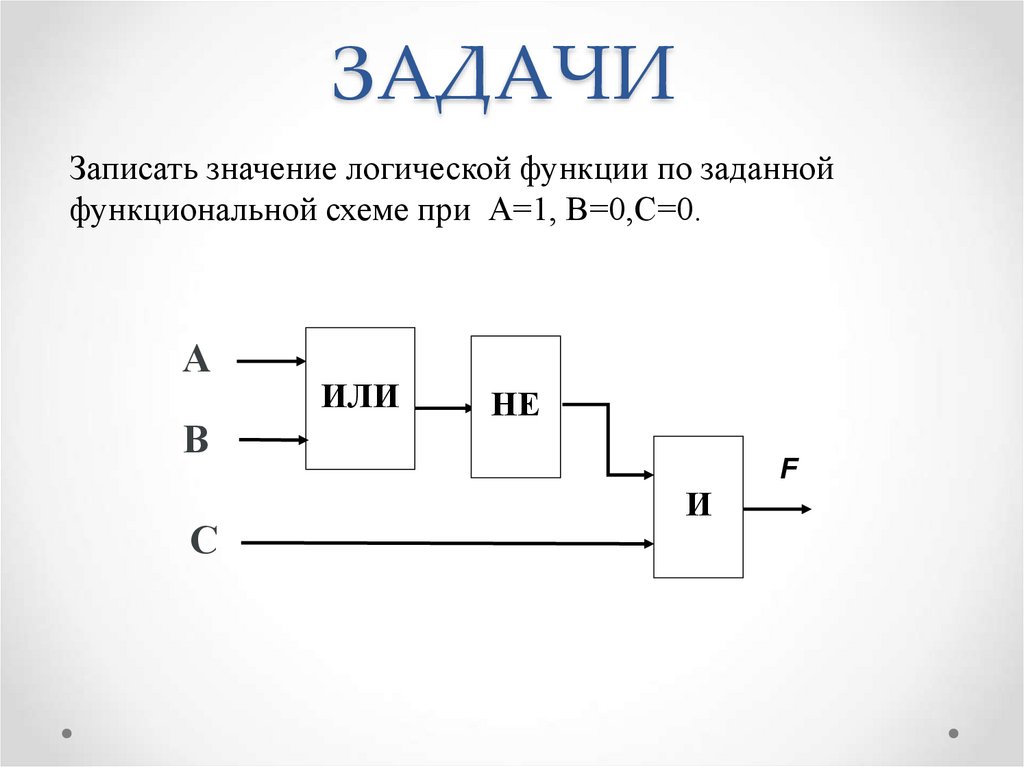
5. ЗАДАЧИ
Записать значение логической функции по заданнойфункциональной схеме при А=1, В=0,С=0.
А
F
ИЛИ
В
С
И
НЕ
6. ЗАДАЧИ
Записать значение логической функции по заданнойфункциональной схеме при А=1, В=0,С=0.
А
ИЛИ
В
С
F
И
НЕ
7. ЗАДАЧИ
Записать значение логической функции по заданнойфункциональной схеме при А=1, В=0,С=0.
А
В
С
ИЛИ
НЕ
F
И
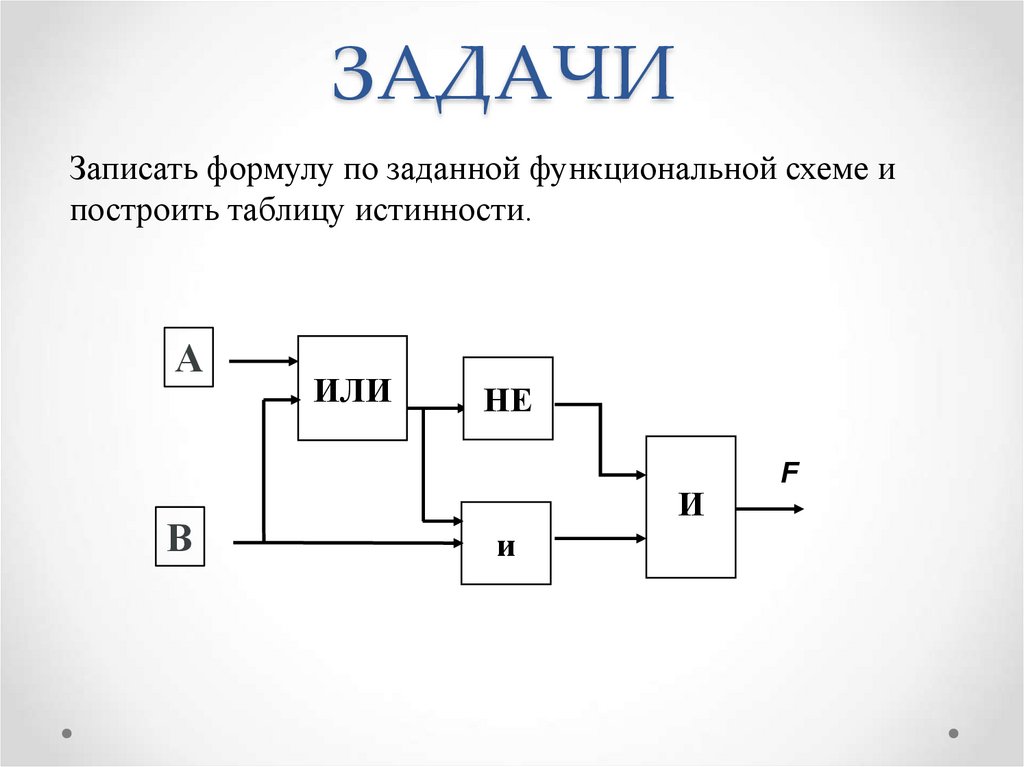
8. ЗАДАЧИ
Записать формулу по заданной функциональной схеме ипостроить таблицу истинности.
А
В
ИЛИ
НЕ
И
и
F
9.
10. Тема: Упрощение логических выражений.
ТЕМА: УПРОЩЕНИЕ ЛОГИЧЕСКИХВЫРАЖЕНИЙ.
11.
Логические функции — составные высказывания —содержат
несколько
простых
высказываний,
соединённых логическими связками (и, или, не,
если...то, тогда и только тогда).
БАЗОВЫЕ ОПЕРАЦИИ:
Инверсия
(отрицание)
Конъюнкция
(логическое
умножение)
Дизъюнкция
(логическое
сложение)
НЕ, Неверно, что…
И
ИЛИ
¬A, A
A&B, AЛB, A*B AVB, A+B
Импликация (следование)
Эквивалентность
(равносильность)
Если…, то…
Тогда и только тогда,
когда…
A→B
A↔B, A≡B
12. Основные законы формальной логики
Закон
тождества
А=А
Закон
непротиворечия
А& A=0
Закон
исключения
третьего
А А=1
Закон двойного
отрицания
А=А
• В процессе рассуждения
нельзя подменять одно
понятие другим
• Не могут быть
одновременно истинными
суждение и его отрицание
• Высказывание может быть
либо истинным либо
ложным, третьего не дано
• Если отрицать дважды
некоторое суждение, то
получается исходное
суждение
13. Свойства констант
• 0=1• А 0=А
• А 1=1
1=0
А&0=0
А&1=А
14. Законы алгебры логики
• ИдемпотентностьА А=А
А&А=А
• Коммутативность
А В=В А
А&В=В&А
• Ассоциативность
А (В С)= (А В) С
А &(В & С)= (А & В) &С
15. Законы алгебры логики
• ДистрибутивностьА (В & С)= (А В) &(A С)
А & (В С)= (А & В) (A&С)
• Поглощение
А (А & В)=А
А & (А В)=А
• Законы де Моргана
(А В)= А& В (А &В)= А В
16. Законы алгебры логики
Огастес де МОРГАНМорган Огастес (Августус) де (27.6.1806-18.3. 1871) - шотландский математик и
логик. Секретарь Королевcкого астрономического общества (1847г.), член
Лондонского королевского общества. Первый президент Лондонского математического
общества. Родился в Мадуре (Индия). Учился в Тринити-колледж (в Кембридже).
Профессор математики в университетском колледже в Лондоне. Основные труды по
алгебре, математическому анализу и математической логике. В теории рядов описал
логарифмическую шкалу для критериев сходимости; занимался теорией расходящихся
рядов. Один из основателей формальной алгебры. Продолжая работы Дж. Пикока,
Морган в 1841-1847 гг. опубликовал ряд работ по основам алгебры. В трактате
"Формальная логика или исчисление выводов необходимых и возможных" (1847г.),
Морган некоторыми своими положениями опередил Дж. Буля. Позднее Морган
успешно изучал логику отношений - область, не охваченную исследованиями
предшественников. Написал много исторических работ, в частности книгу "Бюджет
парадоксов" (1872г.). Большой вклад внес также в дедуктивную логику вообще и
математическую в частности. Лондонское математическое общество учредило медаль
им. О. Моргана.
17
17.
Правила заменыопераций
• Импликации
А В = А B
А В = B A
• Эквивалентности
А В = (А&B) ( A& B)
А В = (А B) ( A B)
А В = (А B) & (B A)
18. Правила замены операций
Упрощение сложныхвысказываний
• - это замена их на равносильные на основе
законов алгебры высказываний с с целью
получения высказываний более простой формы
19. Упрощение сложных высказываний
Основные приемызамены
X=X 1
X=X 0
1=А А
0=В В
Z=Z Z Z
C=C C C
Е= Е
- По свойствам констант
- По закону исключения третьего
- По закону непротиворечия
- По закону
идемпотентности
- По закону двойного отрицания
20. Основные приемы замены
ПримерУпростить: А В А В
По закону дистрибутивности вынесем А за скобки
А В А В= А (В В)= А 1= А
Упростить: (А В )& (А В)
Упростить: ( X Y )
21. Пример
Равносильные преобразования логическихформул имеют то же назначение, что и
преобразования формул в обычной алгебре.
Они служат для упрощения формул путём
использования основных законов алгебры
логики.
22.
Упрощение логических выраженийПод упрощением формулы, не содержащей операций
импликации
и
эквивалентности,
понимают
равносильное
преобразование,
приводящее
к
формуле, которая либо содержит по сравнению с
исходной меньшее число операций конъюнкции и
дизъюнкции и не содержит отрицаний неэлементарных
формул, либо содержит меньшее число вхождений
переменных.
23. Упрощение логических выражений
Алгоритм упрощения логическихвыражений
24. Алгоритм упрощения логических выражений
Рассмотрим на простых примерах некоторыеприемы и способы, применяемые при упрощении
логических формул, знакомые нам из алгебры.
Закон исключения
третьего:
№ 1. Упростим выражение: ¬A&B∨¬A&¬B
¬A⋅B+¬A⋅¬B =¬A⋅(B+¬B)=¬A⋅1=¬A
Ответ: ¬A&B∨¬A&¬B=¬A. Закон исключения
третьего:
№ 2. Упростим выражение: ¬A&(A&¬B)&¬B.
¬A⋅(A⋅¬B)⋅¬B =(¬A⋅A)⋅(¬B⋅¬B) = 0
Ответ: ¬A&(A&¬B)&¬B=0.
25.
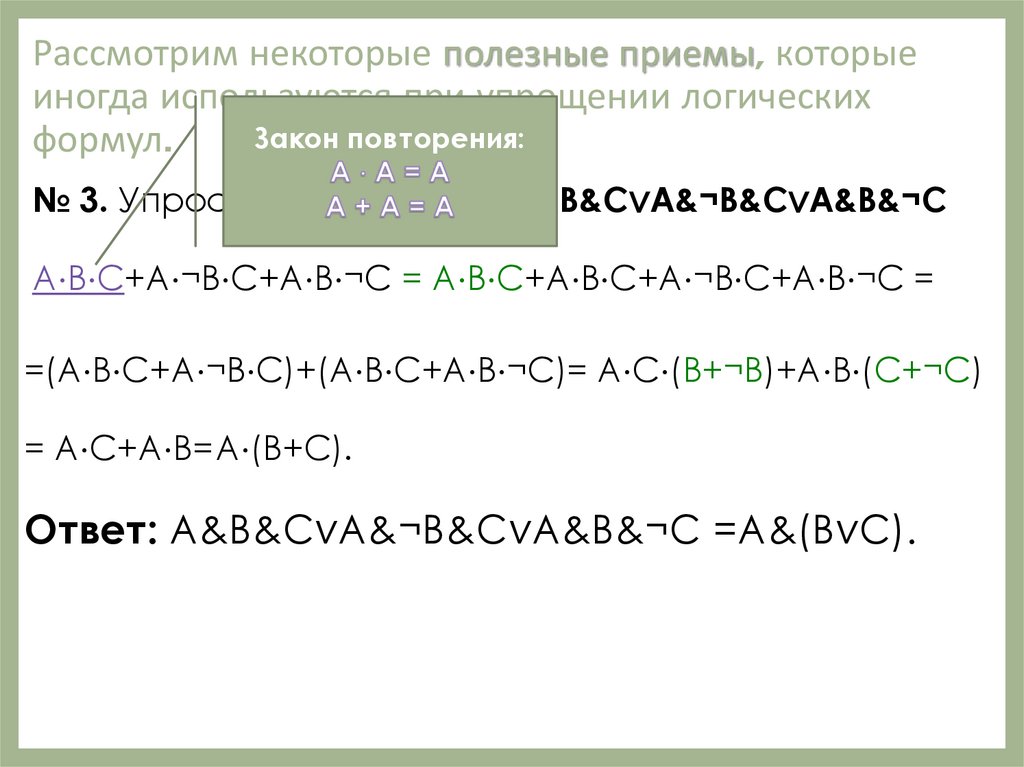
Рассмотрим некоторые полезные приемы, которыеиногда используются при упрощении логических
Закон повторения:
формул.
№ 3. Упростим выражение А&B&C∨A&¬B&C∨A&B&¬С
A⋅B⋅C+A⋅¬B⋅C+A⋅B⋅¬C = A⋅B⋅C+A⋅B⋅C+A⋅¬B⋅C+A⋅B⋅¬С =
=(A⋅B⋅C+A⋅¬B⋅C)+(A⋅B⋅C+A⋅B⋅¬C)= A⋅C⋅(B+¬B)+A⋅B⋅(C+¬C)
= A⋅C+A⋅B=A⋅(B+C).
Ответ: A&B&C∨A&¬B&C∨A&B&¬C =A&(B∨C).
26.
Рассмотрим некоторые полезные приемы, которыеиногда используются при упрощении логических
формул.
№ 4. Упростим выражение: (¬A∨(B∨C))&((¬A∨B)∨¬C).
(¬A+B+C)⋅(¬A+B+¬C)
Заменим для Закон
удобства
¬A+B
на
переменную
Х
поглощения:
(Х+C)⋅(Х+¬C) = Х ⋅ Х + Х ⋅ ¬С + С ⋅ Х + С ⋅ ¬С =
= Х + Х ⋅ ¬С + С ⋅ Х + 0 = Х + С ⋅ Х = Х
Х = ¬A+B
Ответ: (¬A∨(B∨C))&((¬A∨B)∨¬C)=¬A∨B.
27.
Рассмотрим примеры применения закона де Моргана,при упрощении
логических
формул.
Закон
де Моргана:
№ 5. Упростим выражение: ¬(A∨B)&A.
¬(A+B)⋅A =¬A⋅¬B⋅A = ¬A⋅A⋅¬B =0
Ответ: ¬(A∨B)&A=0.
№ 6. Упростим выражение: ¬A∨¬(A&B&¬B).
¬A+¬(A⋅B⋅¬B) =¬A+¬(A⋅0)=¬A+¬0 =¬A+1 = 1.
Ответ: ¬A∨¬(A&B&¬B)=1.
28.
Рассмотрим примеры, в которых встречаетсяимпликация и эквивалентность.
№ 7. Упростить выражение A→B∨¬A
A→B∨¬A =¬A∨B∨¬A
¬A+B+¬A =(¬A+¬A)+B =¬A+B.
Ответ: A→B∨¬A=¬A∨B.
№ 8. Упростить выражение ¬B∨A↔B∨A.
¬B∨A↔B∨A =¬B∨(A&B)∨(¬A&¬B)∨A.
¬B+(A⋅B)+(¬A⋅¬B)+A =(A⋅B+A)+(¬A⋅¬B+¬B)= А+¬B
Ответ: ¬B∨A↔B∨A=A∨¬B.
29. Рассмотрим примеры, в которых встречается импликация и эквивалентность.
А теперь попробуйте самиУпростите логическое выражение:
¬(A∨¬B)∨¬(A∨B)∨A&B
Мы рассмотрели простые примеры. Для каждого из них
мы применяли свою последовательность законов логики. Нет
одинакового для всех выражений способа упрощения. Навыки
приходят с опытом.
30. А теперь попробуйте сами
№ 2.Упростите выражениеА ( А В ) ( В В )
А ( А В) 1
А ( А В) А А В
31. № 2.Упростите выражение
№3O Упростите:
А ( А В ) ( В В )






















 informatics
informatics








