7_ZakonomStroenDrevost

1. ЗАКОНОМЕРНОСТИ СТРОЕНИЯ ДРЕВОСТОЕВ (лекция 7)

Научные концепции изучения строения древостоев
2.
Строение древостоев по общим таксационным
показателям
3.
Особенности строения молодняков
4.
Строение насаждений по морфологическим
показателям
5.
Важнейшие взаимосвязи таксационных показателей
деревьев в древостоях
n, шт
1.
450
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
400
350
300
250
6.
Значение закономерностей в строении древостоев
200
42
150
100
50
0
4
8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72
Д, см
1

2. 1. Научные концепции изучения строения древостоев

Основаны на законах диалектики:
1. единства и борьбы противоположностей,
2. перехода количества в качество,
3. отрицания отрицания
В результате взаимодействия деревьев между собой в процессе
роста и развития, влияния окружающей среды и реакции
организмов на эти влияния, таксационные показатели деревьев в
древостое оказываются чрезвычайно изменчивыми и в то же время
закономерно взаимосвязанными между собой.
Диапазон изменения таксационных показателей в лесных
массивах оказывается значительно шире, чем в отдельном
древостое.
На строение древостоев влияют природные факторы: экологогеографические (условия местопроизрастания), генетические
(наследственная изменчивость), биоценотические (происхождение,
полнота, породный состав, возрастное строение и др.) и
антропогенные.
2

3. Формы причинных связей явлений:

1. механическая причинность, при которой
взаимоотношения между причинной и следствием строго
однозначны
( при одинаковых d1,3, h и f разные деревья имеют
равные Vств)
2. вероятностная или статистическая причинность
(вероятностный детерминизм), когда закономерность
представляет собой диалектическое единство
необходимых и случайных событий.
Лесная таксация как наука накопила значительный
материал, свидетельствующий, что в строении древостоев
имеется ряд закономерностей, использование которых
создает прочную теоретическую основу учета лесов.
3

4. Научные концепции изучения строения древостоев

Вейзе, Вимменауэра в XIX в. установли, что в чистом
одновозрастном древостое число деревьев с d1,3 < Дср составляет
57,5 %
В 1902 году Фекете расположил деревья в ельниках с
различными Дср в порядке возрастания d1,3, разделил ряд на 10
групп с равным числом стволов и для границ каждой из них
определил d1,3.
В 1903 году Шиффель предложил
Положение дерева в древостое в порядке последовательного
увеличения его d1,3, выраженное в процентах от общего числа
деревьев, было названо рангом дерева Pn,
а относительные значения диаметров этих стволов в долях Dср
– редукционными числами диаметра Rd:
Pn
Rd
0
0,56
20
0,77
40
0,90
60
1,06
80
1,17
100
1,48
4

5.

Понятия рангов и редукционных чисел были распространены в
последующем и на остальные таксационные показатели древостоя.
Фактические исследования в этом направлении были продолжены в
трудах зарубежных ученых (Назлунд, Ленротт, Продан, Галая, Корсунь
и др.) в древостоях различных пород и условий местопроизрастания.
Выявилось, что относительные величины
• d1,3
• h
• Vств
• g1,3
• f и hf деревьев,
занимающих определенное место в древостое, практически
одинаковы в нормальных насаждениях различных пород и Dср.
5

6.

Аналитическая связь между рангами и редукционными числами
таксационных показателей в древостоях передается уравнением параболы:
RT а0 а1Рn a2 Pn2 a3 Pn3 a4 Pn4
Дальнейшее широкое обобщение по закономерностям строения
древостоев осуществил проф. А.В. Тюрин.
В 1927 г. Тюрин вводит новое понятие – естественная ступень
толщины как размерность ступени диаметра, выраженной в
десятых долях от Dср, принятого за 1,0.
Такие относительные ступени являются общими для всех
древостоев, позволяют делать обобщения и выводы по строению
леса.
6

7.

Проф. Тюрин устанавливает закон постоянства строения простых
чистых одновозрастных насаждений:
«процентное распределение деревьев по естественным ступеням
толщины не зависит от породы, класса бонитета, полноты, Dср, лишь
несколько зависит от возраста древостоя, и в большей мере – от
интенсивности рубок ухода за лесом».
По однородности строения выделил 4 категории древостоев:
а) тонкомерные (Dср = 10 см);
б) среднемерные (Dср = 20 см);
в) толстомерные (Dср = 30 см);
г) очень толстомерные (Dср = 40 см).
Для обычных целей хозяйства он рекомендует пользоваться лишь
двумя формами строения древостоев (Dср ≤ 25,0 см и Dср ≥ 25,1 см),
а для общей характеристики строения леса ограничиться одним
обобщенным рядом распределения деревьев
7

8.

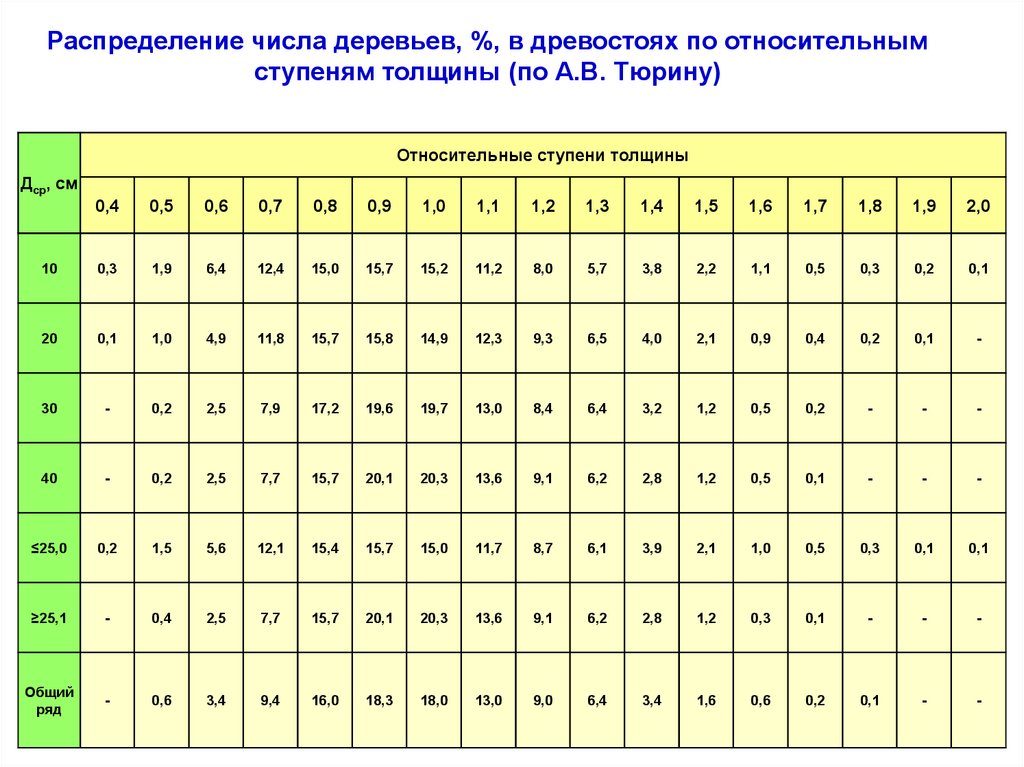
Распределение числа деревьев, %, в древостоях по относительным
ступеням толщины (по А.В. Тюрину)
Относительные ступени толщины
Дср, см
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
10
0,3
1,9
6,4
12,4
15,0
15,7
15,2
11,2
8,0
5,7
3,8
2,2
1,1
0,5
0,3
0,2
0,1
20
0,1
1,0
4,9
11,8
15,7
15,8
14,9
12,3
9,3
6,5
4,0
2,1
0,9
0,4
0,2
0,1
-
30
-
0,2
2,5
7,9
17,2
19,6
19,7
13,0
8,4
6,4
3,2
1,2
0,5
0,2
-
-
-
40
-
0,2
2,5
7,7
15,7
20,1
20,3
13,6
9,1
6,2
2,8
1,2
0,5
0,1
-
-
-
≤25,0
0,2
1,5
5,6
12,1
15,4
15,7
15,0
11,7
8,7
6,1
3,9
2,1
1,0
0,5
0,3
0,1
0,1
≥25,1
-
0,4
2,5
7,7
15,7
20,1
20,3
13,6
9,1
6,2
2,8
1,2
0,3
0,1
-
-
-
Общий
ряд
-
0,6
3,4
9,4
16,0
18,3
18,0
13,0
9,0
6,4
3,4
1,6
0,6
0,2
0,1
-
-
8

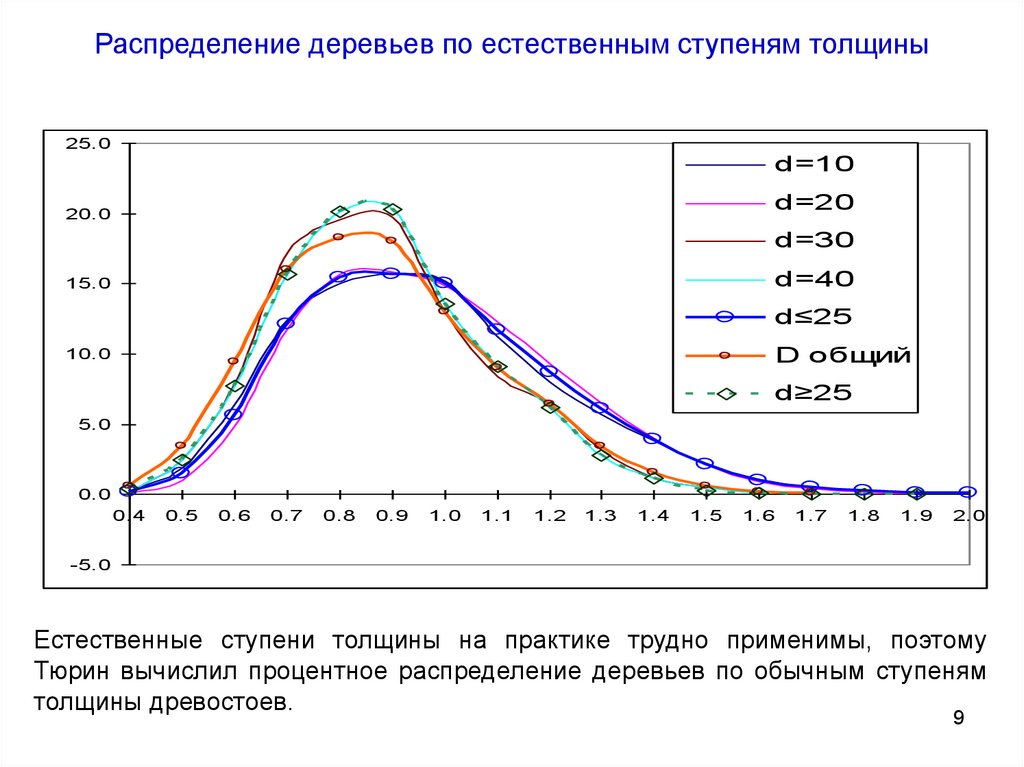
9. Распределение деревьев по естественным ступеням толщины

25.0
d=10
d=20
20.0
d=30
d=40
15.0
d≤25
D общий
10.0
d≥25
5.0
0.0
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
-5.0
Естественные ступени толщины на практике трудно применимы, поэтому
Тюрин вычислил процентное распределение деревьев по обычным ступеням
толщины древостоев.
9

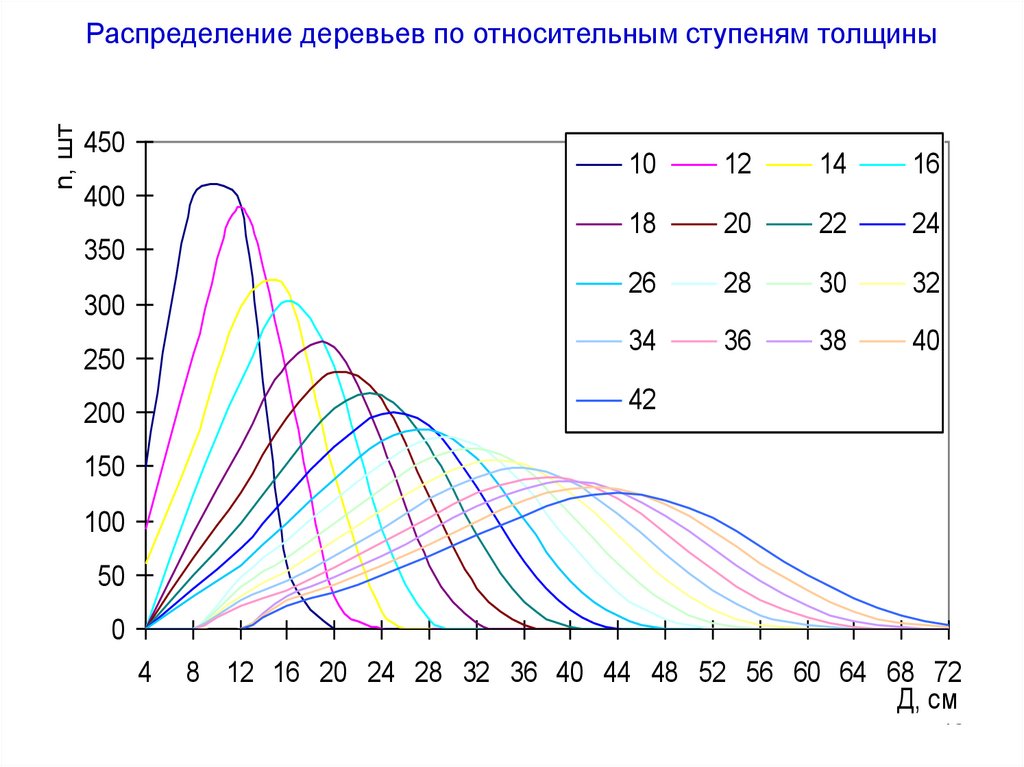
10. Распределение деревьев по относительным ступеням толщины

n, шт
Распределение деревьев по относительным ступеням толщины
450
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
400
350
300
250
42
200
150
100
50
0
4
8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72
Д, см
10

11.

Н.В. Третьяков (1927) изучая строения смешанных и
сложных насаждений продолжил и установил закон
единства в строении насаждений:
«строение элемента леса во всех случаях носит
постоянный характер, независимо от породы, класса
бонитета, Аср, полноты, доли участия в составе
древостоя яруса»
В последующем трудами советских ученых (Анучин,
Давидов,
Захаров,
Дворецкий,
Никитин,
Левин,
Моисеенко, Моисеев, Мошкалев, Фалалеев, Верхунов и
др.) внесен значительный вклад в изучение строения
древостоев по таксационным показателям в насаждениях
различных пород, условий местопроизрастания, средних
возрастов, возрастной структуры, различных полнот,
состава древостоев и других факторов
11

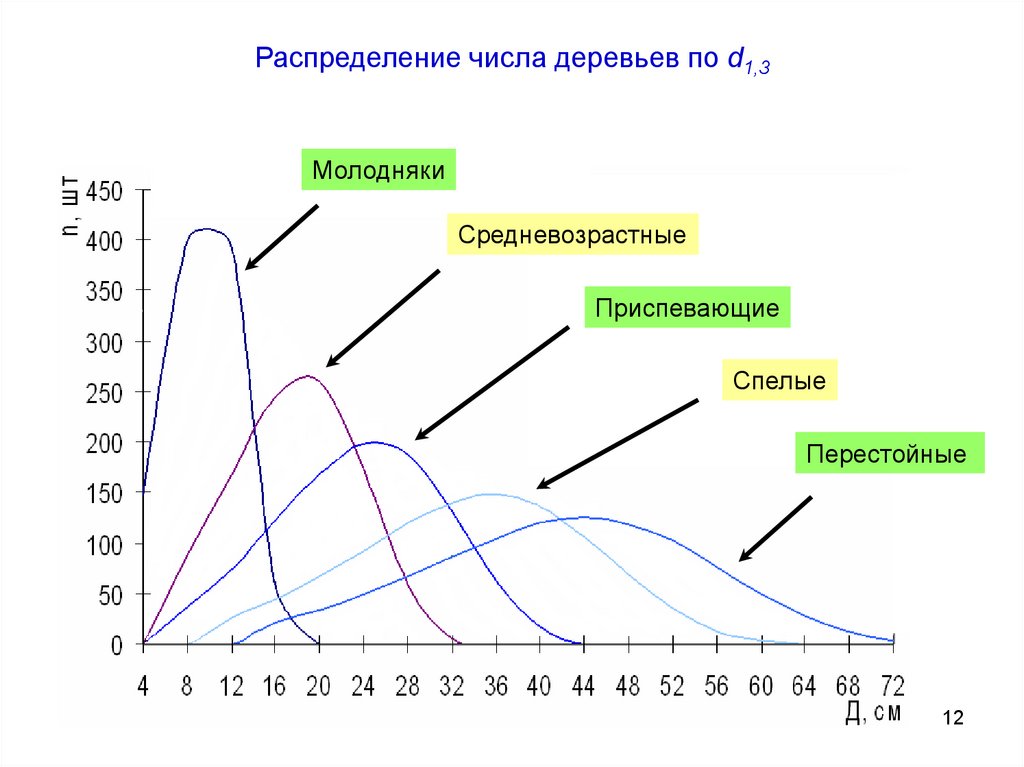
12.

Распределение числа деревьев по d1,3
Молодняки
Средневозрастные
Приспевающие
Спелые
Перестойные
12

13.

В рядах распределения по таксационным показателям в
древостоях меняются место среднего дерева, редукционные числа по
рангам, размах ряда и концентрация процента числа стволов в
относительных ступенях таксационного показателя, величины
асимметрии и эксцесса ряда.
По ступени динамичности строения от природных факторов
выделяются 4 группы таксационных показателей древостоев:
а) с весьма динамичной структурой – d1,3, Vcтв, Zg, ZV;
б) с существенным влиянием возраста леса – h, hf, Zd, Pd, Ph, PV;
в) с малым изменением от структурообразующих факторов - lкр, Ркр;
г) с однородным строением по всем категориям древостоев – q2, f.
Эти ряды распределения описываются различными уравнениями
Пирсона, Грама-Шарлье типа А, нормального распределения и редко
– другими типами (γ – распределение, β – распределение, Пуассона,
Вейбула и др.)
Необходимо разрабатывать нормативно-справочные материалы для
таксации древостоев по лесотаксационным районам вместо всеобщих.
13

14. 2. Строение древостоев по общим таксационным показателям

Одним из краеугольных основ в лесной таксации является
выдвинутая и обоснованная теория среднего дерева древостоя.
Согласно ей, среднее по диаметру дерево признается
одновременно средним и по всем остальным таксационным
показателям.
Следовательно, редукционные числа всех таксационных
показателей для среднего дерева древостоя составляют 1,0 и их
ранги одинаковы (рис)
Ранг среднего дерева древостоя зависит от ряда природных факторов
(порода, состав древостоя яруса, лесорастительные условия, Аср, густота,
возрастная структура) и колеблется в пределах 51-60 %.
14

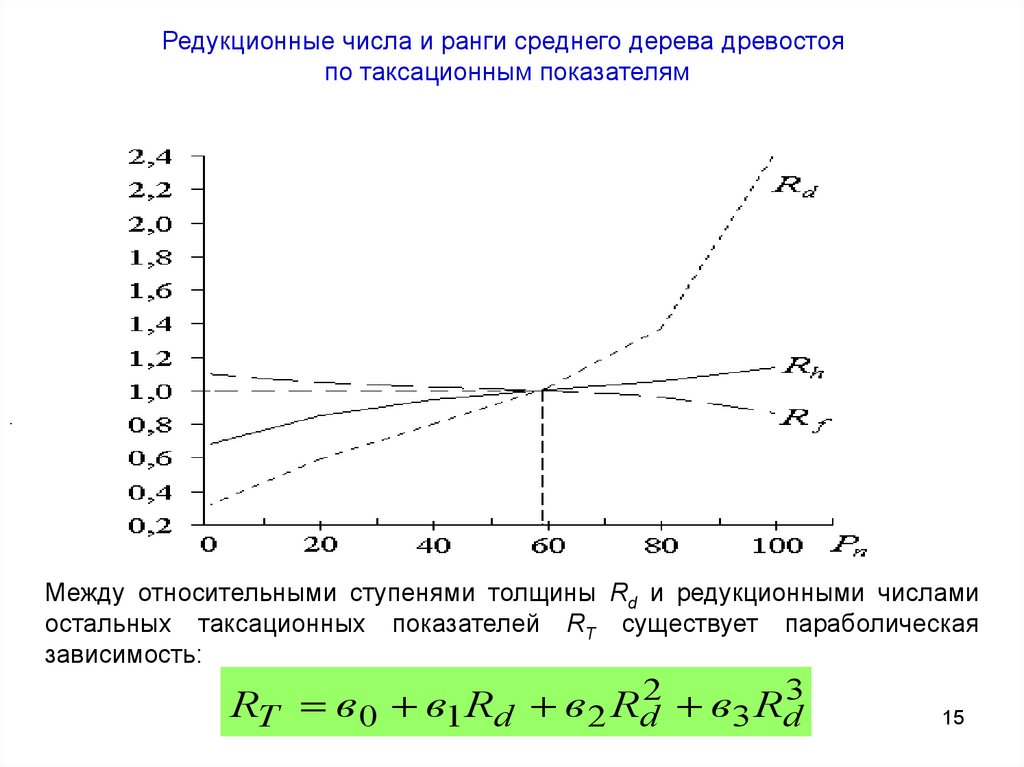
15.

Редукционные числа и ранги среднего дерева древостоя
по таксационным показателям
.
Между относительными ступенями толщины Rd и редукционными числами
остальных таксационных показателей RТ существует параболическая
зависимость:
RT в0 в1 Rd в 2 Rd2 в3 Rd3
15

16.

Рассмотрим особенности строения деревьев по отдельным таксационным
показателям леса.
Возрастная структура древостоев.
Поколение леса состоит из деревьев, возникших в результате возрастной или
восстановительной смены леса.
Строение по диаметрам деревьев.
Изменчивость диаметров Сd деревьев в древостоях зависит от ряда
природных факторов: породы, возраста леса, возрастной структуры
древостоев и др.
В молодняках она составляет 40…60 %, спелых и перестойных древостоях –
22…25 %.
С усложнением возрастной структуры величина Сd закономерно повышается;
в темнохвойных насаждениях она больше, чем в светлохвойных.
Необходимое число замеров для определения Dср древостоя с заданной
степенью точности:
n = Сd2 /
Рd2,
Рd – заданная точность, %, определения Dср древостоя.
16

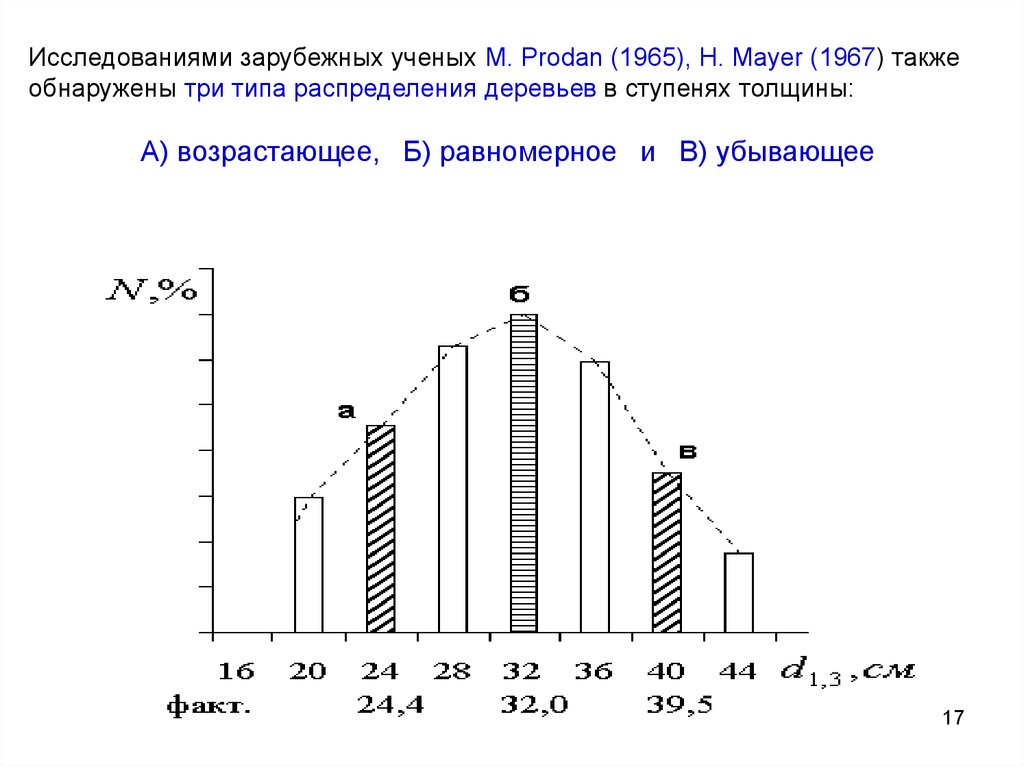
17.

Исследованиями зарубежных ученых М. Prodan (1965), H. Mayer (1967) также
обнаружены три типа распределения деревьев в ступенях толщины:
А) возрастающее, Б) равномерное и В) убывающее
17

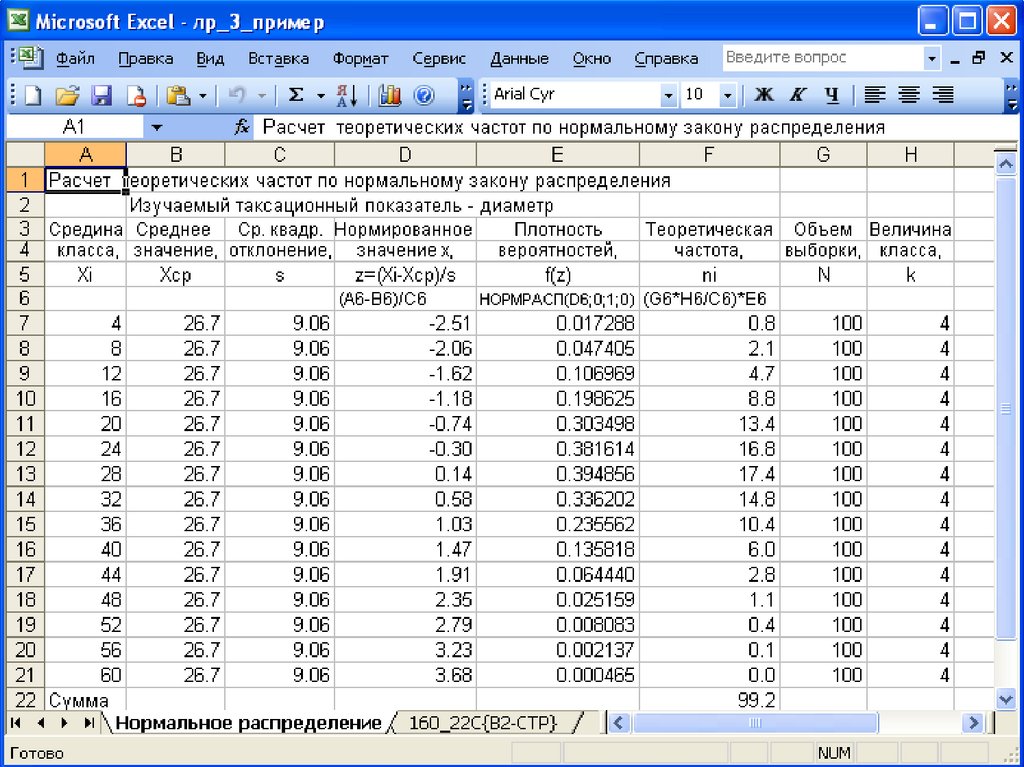
18.

По P. Dagnelie, J. Rodeux (1971),
закон нормального распределения имеет следующий вид
хi x
2
f x
1
2
е
2 2
Многие исследователи (Митропольский, 1971; Никитин, 1966; Мошкалев
и др., 1973 и др.) считают, что можно применять для описания рядов d1,3
обобщенную кривую нормального распределения (Грама-Шарлье типа
А):
Ψ (x) = f(x) – A/6 f (3)(x) + E/24 f (4)(x)
18

19.

Другие ученые (Патацкaс, 1965; Макаренко, 1970; Дыренков, 1973 и др.)
предлагают использовать кривую Пирсона типа I
уi у0 1 х / l1 1 x / l 2
q1
q2
многие зарубежные и некоторые отечественные исследователи, изучая
строение древостоев, предпочтение отдают уравнению Вейбулла
(R.L. Bailey, T.R. Dell, 1973), имеющего вид
g(у) = [с/в (у-а)/в]С-1∙ехр[– (у-а)/в]С,
Наиболее общий вид распределения статистических величин –
распределение Маркова (Колмогоров, 1936; Митропольский, 1971 и др.),
приводящее в предельном переходе к семейству кривых Пирсона
(типа I – VII):
dy/y = [(x+ в)/(c0+c1x+c2x2)]·dx
19

20.

20

21.

Строение по высоте деревьев.
В пределах элементов и поколений леса высота деревьев связана с
положением их в древостое.
Эта связь может быть передана соотношением Rh по рангам деревьев или
же по значениям Rh в относительных ступенях толщины древостоев.
Значения Rh в древостоях по исследованиям проф. А.В. Тюрина
составляют:
в молодняках – 0,75…1,20;
в средневозрастных, приспевающих древостоях – 0,80…1,15;
в спелых, перестойных древостоях – 0,85…1,10.
21

22.

Строение по q2 и f деревьев.
По исследованиям многих ученых, распределение в древостое стволов
по значениям q2 и f подчиняется кривой нормального распределения.
Редукционные их числа Rq2, Rf, составляют:
в самой тонкомерной ступени толщины – 1,10;
самой толстомерной – 0,87.
В сложных древостоях Сибири границы их шире:
Rq2 = 1,21…0,79 (в разновозрастных – Rq2 = 1,25…0,74);
Rf = 1,30…0,72 (в разновозрастных – Rf = 1,35…0,65).
Коэффициент изменчивости q2 деревьев в насаждениях
светолюбивых пород равен 7…8 %,
теневыносливых – 9…12 %.
Варьирование видовых чисел стволов в древостоях несколько шире и
составляет соответственно 8…11 % и 14…20 %.
22

23.

Строение по видовой высоте hf, площади сечения g1,3 и объему
стволов.
Строение древостоев по видовой высоте hf существеннее меняется в
зависимости от возрастных этапов развития поколений и менее значимо – от
возрастной их структуры.
редукционное число видовой высоты деревьев Rhf возрастает в древостоях от
0,88 в самой тонкомерной ступени до 1,00 – в относительной ступени 0,9 и
далее с повышением толщины деревьев остается константным.
Редукционные числа g1,3 деревьев в насаждениях повышаются от 0,25…0,31 в
тонкомерной их части до 2,43…2,89 – в толстомерной.
Границы показателей RV объема стволов несколько шире – от 0,22…0,23 до
2,45…2,89. Значения рассматриваемых признаков совпадают, начиная от
относительной ступени толщины 0,9 и выше,
Поскольку
RV = Rg Rhf ,
а в тонкомерной части древостоев Rg > RV .
23

24.

Строение древостоев по показателям прироста деревьев.
По одновозрастным древостоям результаты исследований изложены в
монографиях проф. П.В. Воропанова (1961), проф. М.Л. Дворецкого (1964), В.
Антанайтиса (1976,1986), Е. Assmann (1961, 1970), W. Erteld (1957); по
разновозрастным – П.М. Верхунова (1975, 1976, 1979).
Наиболее изучено строение древостоев по текущему приросту диаметра
Zd деревьев, имеющего важное значение в дендрохронологии и разработке
методов учета прироста леса.
Редукционные числа RZh деревьев составляют:
0,26…2,09 – в одновозрастных;
0,07…3,53 – в разновозрастных древостоях.
по данным П.М. Верхунова, границы RZV в возрасте
61-120 лет составляют 0,05…3,40
в 241-320 лет составляют 0,19…2,67
В разновозрастных древостоях RZV составляют в пределах 0,04…3,64.
24

25.

Коэффициенты изменчивости составляют
в одновозрастных насаждениях:
Zd = 35…56 %
Zh = 20…46 %
ZV = 47…88 %
РV = 29…38 %
в разновозрастных
Zd = 43…78 %
Zh = 48…89 %
ZV = 57…71 %
РV = 59…104 %.
25

26.

3. Особенности строения молодняков
Строение молодняков отличается значительно большим размахом
таксационных показателей деревьев по относительным ступеням и
величиной их варьирования, чем в спелых насаждениях.
Формируемые естественные молодняки являются условно
одновозрастными, но при условии сохранения подроста условно
разновозрастными.
По исследованиям В.С. Моисеева (1971), редукционные числа
возраста деревьев RА
для молодняков хвойных пород составили 0,7-1,3,
лиственных – 0,5-1,5.
На это явление чаще всего влияют лесорастительные условия,
технология лесозаготовок и другие условия.
26

27.

Коэффициент изменчивости d1,3 в молодняках составляет
Сd = 40…60 %.
Ранги средних деревьев по диаметру
по сосне, осине – 60…70 %;
ели, березе – 70…75 %.
Редукционные числа Zd имеют границы в древостоях:
Rd = 0,2…2,5 при Dср ≤ 5 см;
Rd = 0,2…2,0 при Dср = 6…12 см.
Строение по Rh и изменчивость высот деревьев Сh в молодняках
также обусловлены величиной Dср древостоев, рассматриваемые
признаки составляют:
Dср ≤ 4 см
Сh = 40…50 %
Rh = 0,4…2,0
Dср = 5… 8 см
Сh = 30…40 %
Rh = 0,5…1,7
Dср = 9…12 см
Сh = 20…30 %
Rh = 0,6…1,5
27

28. 4. Строение насаждений по морфологическим показателям

К морфологическим показателям леса относятся строение
полога древостоев и пространственное размещение составляющих
их деревьев.
Показатели морфологии полога насаждения:
• форма и размеры крон,
• виды полога,
• сомкнутость крон и полога,
• густоту и расстояние между деревьями, закономерности
распределения деревьев по размерам крон
• закономерные взаимосвязи морфологических и таксационных
признаков.
28

29.

В последующем исследования в этом направлении проводились
многими учеными (Баранов, Моисеев, Сухих, Харин, Киреев,
Дмитриев, Кузьмичев, Любимов, Вавилов, Белов и др.)
Редукционные чиселе Rlк
0,29…1,90 в молодняках
0,4…1,57 в перестойных насаждениях
Редукционных чисел Рк
0,32 - 1,81 в молодняках
0,45 - 1,56 в перестойных насаждениях .
Редукционные числа Дк
для сосны – 0,4…2,0;
ели
– 0,2…2,0;
березы
– 0,4…2,0;
осины
– 0,4…1,8;
лиственницы – 0,35…1,70
29

30. 5. Важнейшие взаимосвязи таксационных показателей деревьев в древостоях

Научно-методической основой методов лесной таксации являются
существующие математические взаимосвязи таксационных
показателей деревьев между собой. Их выявление имеет важное
теоретическое и практическое.
Чаще всего связь выражается уравнением
2
3
h a0 a1d1,3 a 2 d1,3 a3 d1,3
Диаметр и высота деревьев
h = а * d1,3 + в;
hd1,3 = а * d1,3 + в;
h = а * ℓgd1,3 + в;
h = а * ℓgd1,3 + в * d1,3 + с;
Теснота связи между d1,3 и h деревьев в молодняках 0,94, в
перестойных 0,70
30

31.

Шнейдель выявил тесную коррелятивную связь в древостоях
между d1,3 и V стволов (кривая объемов)
Vств ad1в,3
Копецкий установил наличие прямолинейной тесной связи в
древостоях между g1,3 и V стволов (прямая объемов):
в
Vств ag1,3
Н.В. Третьяков для элементов леса:
d1,3f = a0 +a1 d1,3;
qn g1,3 = a0 + a1 g1,3;
qn = a0 + a1 ℓg d1,3.
hf = a0 + a1 h;
qnh = a0 + a1 h;
31

32. Связь между Zd и d1,3 деревьев

Z d a 0 a1d1,3
a2 d1, 3
a
Z d a 0 d1,3 e
2
Z d a0 a1d1,3 a2 d1,3
2
ZV f(Zd , d1,3 ,h);
РV = f(Zd, Zh, d1,3, h).
32

33.

В одновозрастных древостоях выявлены тесные прямые связи между
диаметрами крон Дк и d1,3 деревьев
Менее тесная связь обнаруживается между Дк и h деревьев
d1,3 или
h аД кр в
2
d1,3 или h аД кр
вД кр с
3
2
h
аД
вД
d1,3 или
кр
кр
.
кр
сД кр е
С объемами крон Vк в древостоях тесно (η = 0,80-0,89) коррелируют объемы
стволов:
ℓgVств = а ℓg Vк + в.
33

34.

Исследованиями В.В. Кузьмичева (1977) установлены функции
прироста по диаметру древостоев от возраста, средней высоты,
Дср, среднего расстояния между деревьями и запаса на 1 га
Текущий прирост запаса определяется по формуле
M е
a1
a3
a4
a2
N
Д
H cp
cp
Выявлены также существующие значительные прямые связи
между протяжением кроны lк и диаметрами d1,3, высотами h и
объемами V стволов
(η соответственно равна 0,48…0,81; 0,56…0,81 и 0,66…0,73).
П.С. Кондратьев (1961) установил, что прирост ZV и качество
древесины зависят от площади питания и размеров крон.
А. Bouček (1966) выявил связи между объемом кроны и Zd, Zh и
ZV деревьев в ельниках (r = 0,84; 0,51 и 0,88).
L. Маdаč (1967) установил характер изменения в насаждениях
показателя ZV стволов, приходящегося на 1 м2 поверхности кроны
деревьев, возможно лишь на основе учета требований древесных
пород к площади питания, физиологической специфики и
34
правильного формирования структуры древостоя.

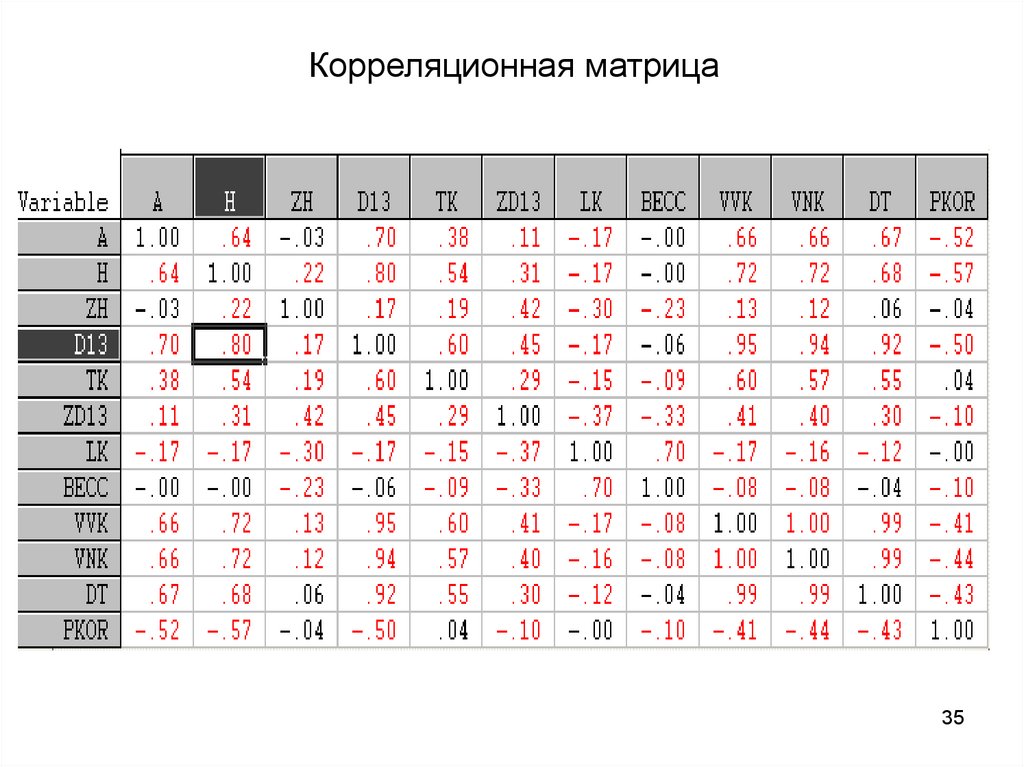
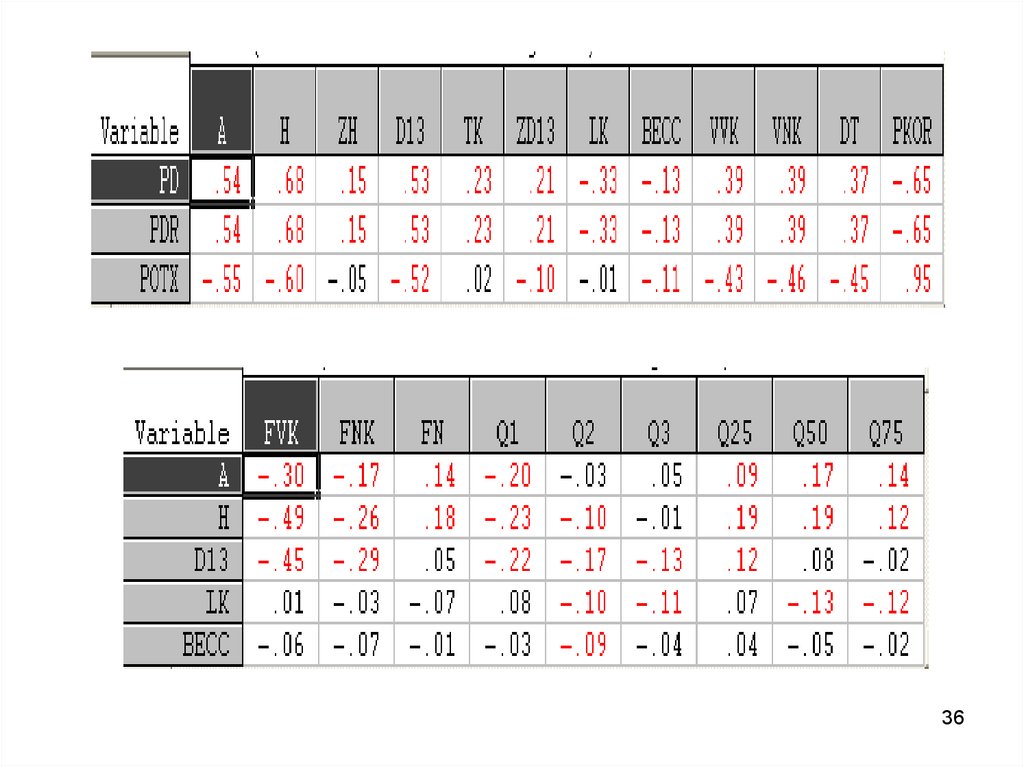
35. Корреляционная матрица

35

36.

36

37. 6. Значение закономерностей в строении древостоев

1. Выявленные закономерности в строении
древостоев служат основой создания оптимальной
структуры лесов будущего
Закономерности строения древостоев:
а) позволяют с высокой точностью определять
запас древостоев, вычислять выход сортиментов,
обосновать методы учета прироста запаса леса;
б) служат основой составления различных
лесотаксационных таблиц и нормативов учета леса;
в)позволяют правильно выявить элементы и
поколения леса;
2.
3. Выявленные закономерности строения древостоев
позволяют математически моделировать на ПК процессы
роста и развития насаждений
37

38.

4. При разработке автоматизированных методов
дешифрирования аэрофотоснимков, применении других
способов дистанционного изучения лесов,
5. В лесоустройстве при разработке новых
автоматизированных систем и оценке лесных ресурсов
• космическая и лазерная таксация лесов,
• выборочно-статистическая инвентаризация и
• фотостатистический метод учета лесов в крупных
лесных массивах,
• автоматизированное определение таксационных
показателей древостоев и т.п.
38

39. STATISTICA

STATISTICA
Системный подход к анализу данных.
Системный подход к анализу данных.
Представительства компании StatSoft:
Англия, Франция, Германия, Италия, Польша, Португалия,
Бенелюкс, Южная Африка, Греция, Испания, Скандинавия,
®
Россия, Япония, Корея, Тайвань, Австралия, Бразилия,
StatSoft ®Russia
39
Израиль, Юго-Восточная Азия.
StatSoft Russia

40. Структура пакета

Основное
окно
Таблицы
данных
Графики
Таблицы
результатов
40

41.

Подготовка данных
Данные Стандартизация Подмножества
Формат
Фильтрация
Веса
Текстовые значения
41

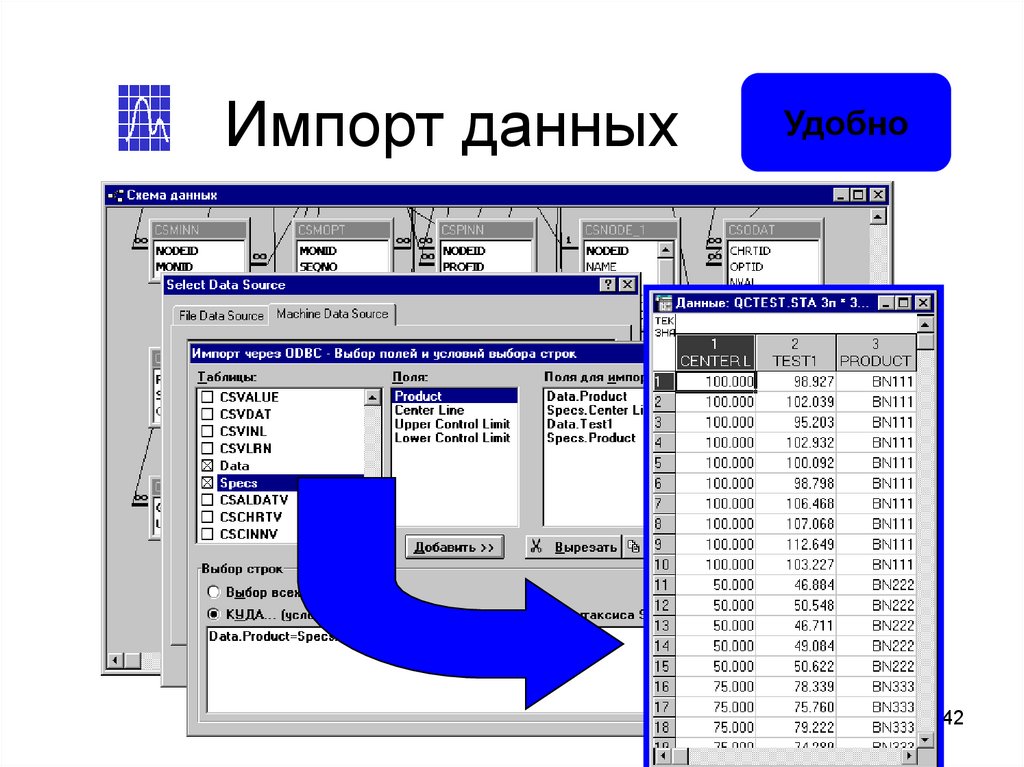
42.

Импорт данных
Удобно
42

43.

Анализ данных
STATISTICA
включает все
методы
статистического
анализа данных:
от классических
до самых
современных
Для удобства
анализа методы
разделены на
43
модули

44.

Анализ данных
Основные
статистики
Нелинейное
Факторный
Множественная
Временные
ряды и
ирегрессия
таблицы
оценивание
анализ
прогнозирование
44

45. Графики

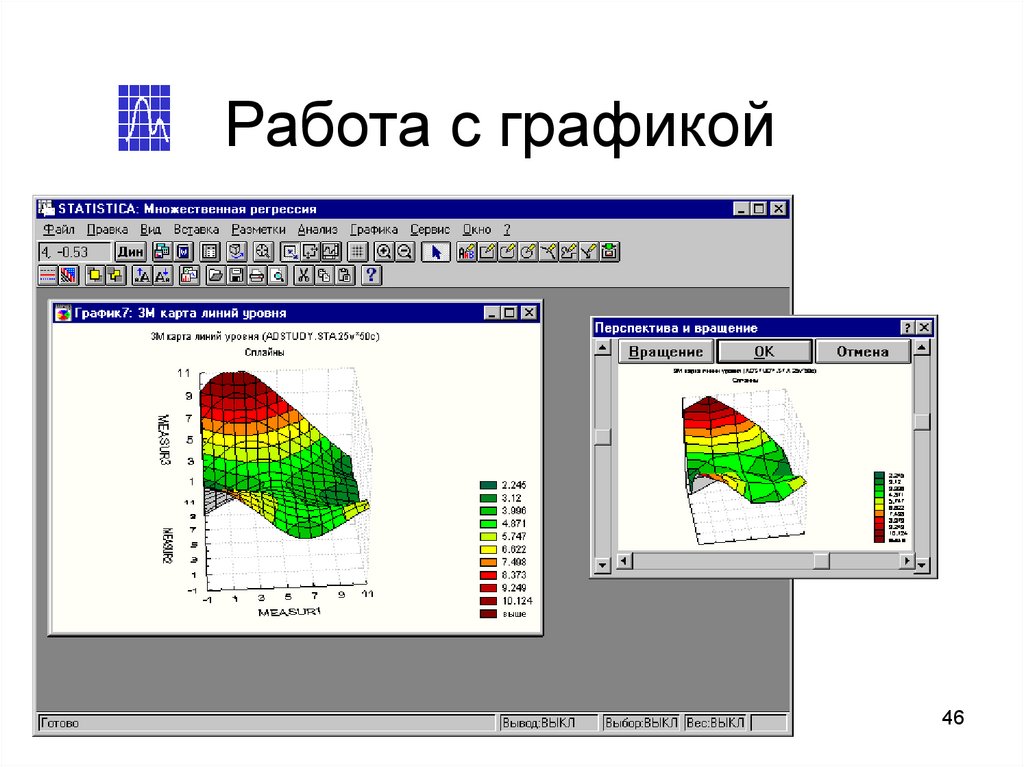
45

46. Работа с графикой

3D-вращение
и перспектива
46

47. Работа с графикой

Дальнейшая
настройка
47

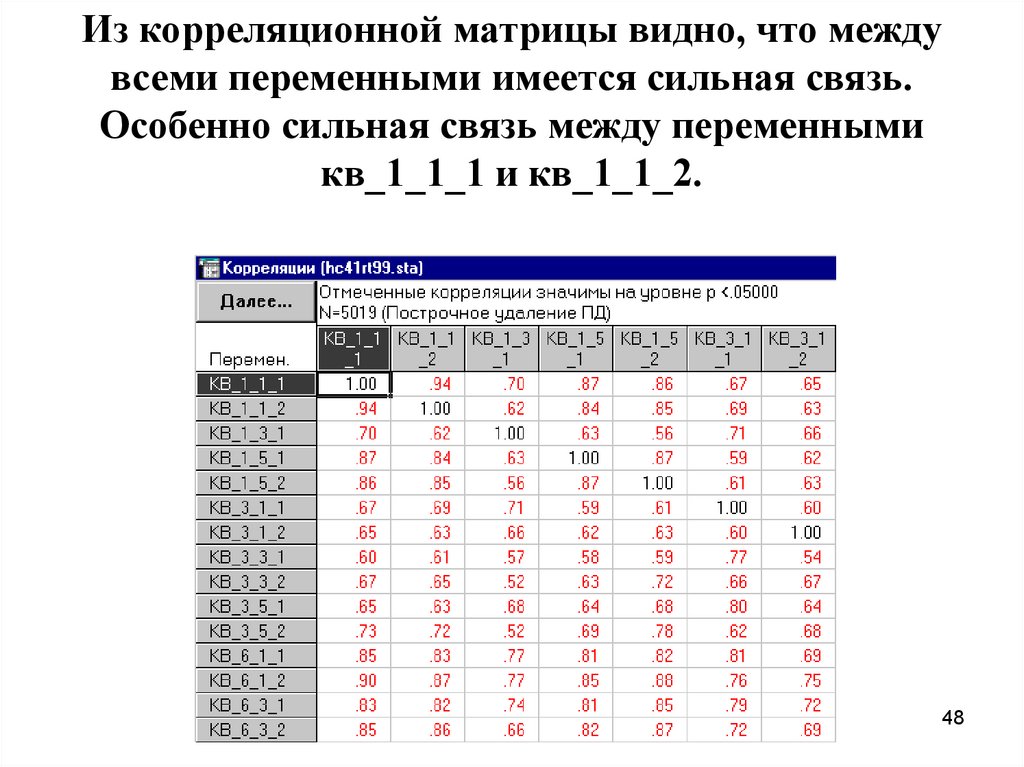
48.

Из корреляционной матрицы видно, что между
всеми переменными имеется сильная связь.
Особенно сильная связь между переменными
кв_1_1_1 и кв_1_1_2.
48

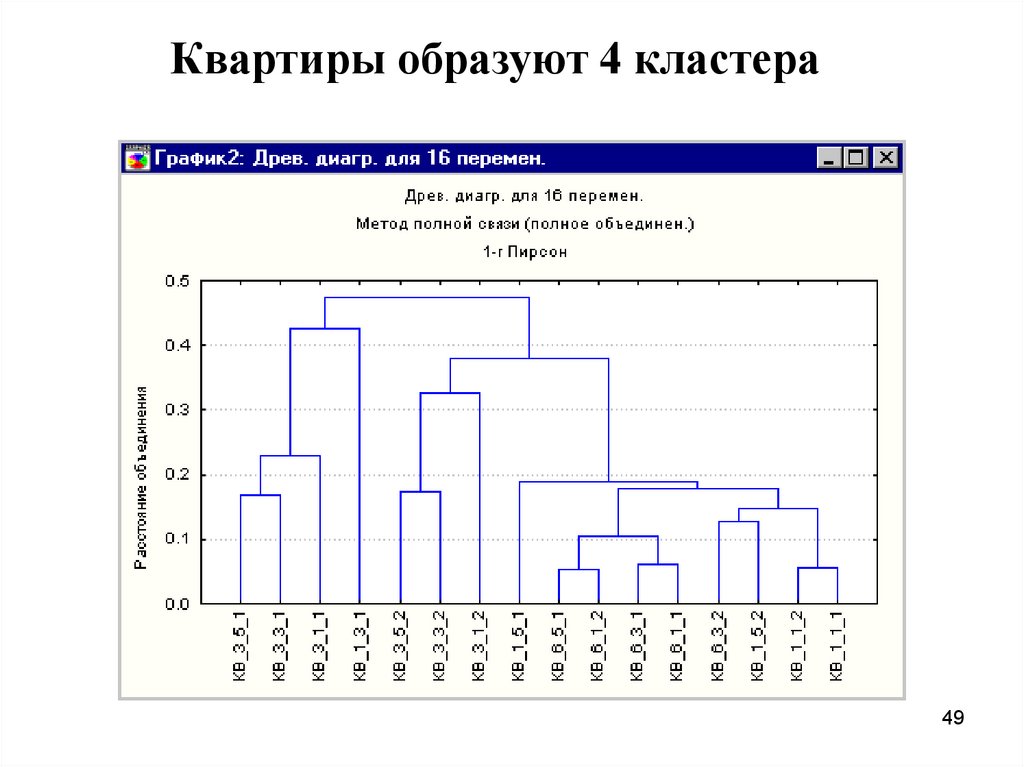
49.

Квартиры образуют 4 кластера
49