Radiometriya_22

1. Радиометрия приборы практика

2. Радиометрия

РАДИОМЕТРИЯ (от лат. radio - излучаю и
греч. metreo-измеряю), регистрация и
измерение активности излучений,
испускаемых ядрами радионуклидов (числа
распадов в единицу времени) с помощью
радиометрических приборов.
Родоначальниками Р. можно считать Э. Резерфорда и Х. Гейгера,
впервые осуществивших с помощью искрового счётчика
определение числа a-частиц, испускаемых в 1 сек 1 г Ra
(удельная активность).

3. Основная цель…

4. Радиометрические величины

Активность - ожидаемое число спонтанных ядерных превращений в единицу
времени [распад в секунду - Бк]
Флюенс, , - число частиц падающих на сферу с поперечным сечением dS:
=
Единица флюенса:[м-2]
dN
dS
Плотность потока, , - число частиц, падающих на сферу с поперечным
сечением dA за единицу времени:
d
=
Единица плотности потока: [м-2 с-1]
dt
Удельная активность:
где: A - измеренная удельная активность [Бк/кг].
N – скорость счёта [имп/с];
e – эффективность регистрации;
m – навеска анализируемой пробы [кг].
A
N
e m
Объёмная активность:
Единица объёмной активности: [Бк/м3]
A
N
e V

5. Объект измерения

Агрегатное состояние объекта измерения
жидкость
твердое
газообразное

6. Измеряемые величины

Вода
Бетасум<1 Бк/кг
Альфасум<0,2 Бк/кг
Воздух
ОАU<0,033 Бк/м3
ОАTh<0,022 Бк/м3
Продукты
питания
<100 Бк/кг (Sr-90)
<10 Бк/кг (Pu-238)
Древесина
(топливная).
<370 Бк/кг (Sr-90)
<1400 Бк/кг (Cs-137)
Древесина
(строительная).
<5200 Бк/кг (Sr-90)
<370 Бк/кг (Cs-137)
Медицина
12 ГБк/тело (Re-188)
4 ГБк/тело (I-125)
Плотность
потока
10 /40 частиц/(см2мин)
Бета
1 частиц/(см2мин)
Альфа (сним)

7.

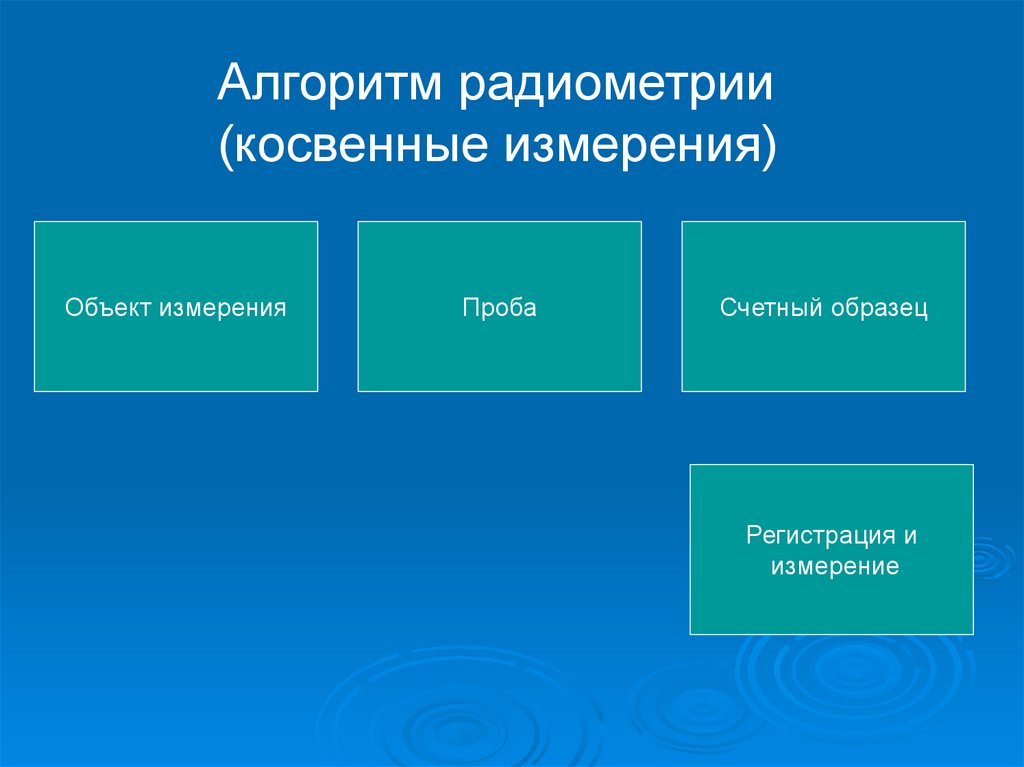
Алгоритм радиометрии
(косвенные измерения)
Объект измерения
Проба
Счетный образец
Регистрация и
измерение

8.

Алгоритм радиометрии
(прямое измерение)
Объект измерения
(Проба,
Счетный образец)
Регистрация и
измерение

9. Проба

Общие принципы пробоотбора:
Проба должна быть представительной;
Пробоотбор и дальнейший анализ
объектов взаимозависимы

10. Регистрация и измерение

По способу регистрации радиоактивного
излучения радиометрические методы
делятся на:
ионизационные (измерение общего
ионизационного эффекта излучения)
импульсные (счёт числа частиц α- или βизлучения или квантов γ-излучения).
распределение активности по поверхности
изучаемого объёма обычно определяют
методом фотоэмульсионной
авторадиографии.

11. Абсолютные измерения

Измерение абсолютной активности
применимо когда:
Известен точный радионуклидный состав пробы;
Учитываются особенности схемы распада
радионуклида;
Самопоглощение, саморассеивание, обратное
рассеивание, геометрия измерения, поглощение
воздухом и окном детектора, эффективность
детектора и его мертвое время

12. Относительный способ измерения (метод компаратора)

измерение активности альфа –, бета – излучающих
радионуклидов в исследуемой пробе и
сопоставление её с активностью стандарта (образец
сравнения контрольный - ОСК).

13. Счетный образец

по способу приготовления источника:
«бесконечно тонкий» и «толстый» источник,
«перевода метки в газ», «полного испарения проб».
по геометрии измерений:
методы определённого телесного угла и «4πсчёта».
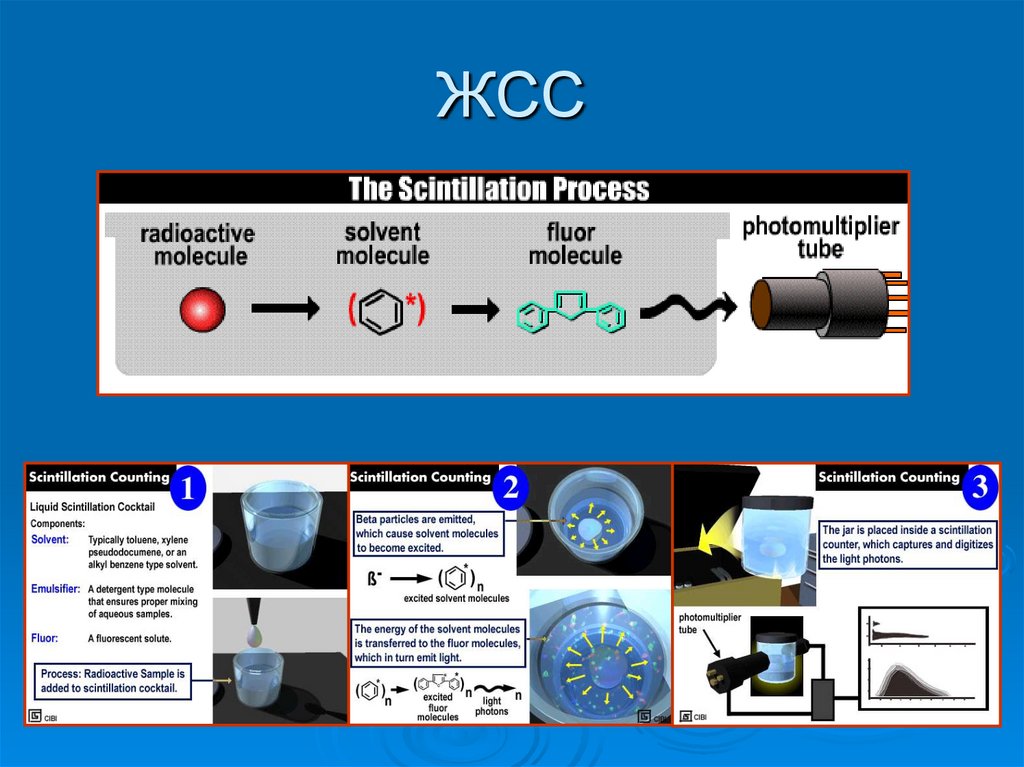
по используемым физическим явлениям:
калориметрический, метод жидкостного
сцинтилляционного счёта, методы счётчиков
внутреннего наполнения, ионизационных камер,
масс-спектрометрический, эмиссионный
спектральный, метод совпадений и др.

14. Способы приготовления счетных образцов

Выпаривание раствора на подложке.
Осаждение из суспензии
Отстаивание осадков;
Фильтрование осадков;
Центрифугирование
Электролитическое осаждение.
Электрокапиллярное напыление
Специальные способы:
Напыление в вакууме:
Катодное распыление:
Сорбционное поглощение и др.

15. Требование к образцу сравнения

Соответствовать метрологически аттестованным значениям
активности, свойствам и составу материала (уменьшает
систематическую погрешность).
Быть максимально приближенным по своим химическим и
физическим свойствам к типичным счетным образцам.
По типу и характеристикам излучения быть близкими к
типичному составу измеряемых образцов. (232Th, 238U, 40K, 90Sr,
137Cs)
Нуклидный состав образца не должен меняться со временем.

16. Область применения

Экология/здравоохранение
Медицина
Технология

17. Основные задачи решаемые в экологии и здравоохранении

Измерение радиоактивности в:
Продуктах питания
Воде
Воздухе
Стройматериалах
Местности
Помещениях

18. Основные задачи решаемые в медицине

Определение радиоактивности в фарм
препаратах.
Планирование дозовых нагрузок при
проведении терапии.

19. Основные задачи решаемые в технологии

Определение радиоактивности в
производимой продукции
Контроль характеристик используемых
ИИ

20. Выбор детектора

Тип детектора:
Ионизационный;
Сцинтилляционный;
Полупроводниковый.
Материал из которого изготовлен детектор:
ZnS(Ag)
CsI(Tl)
Пластмассовый сцинтиллятор.
Агрегатное состояние и размеры детектора:
Монокристалл/жидкий сцинтиллятор или рабочий
газ;
Размеры детектора, толщины входных окон.

21. Основные характеристики радиометров

Чувствительность;
Эффективность регистрации блока
детектирования.

22. Чувствительность

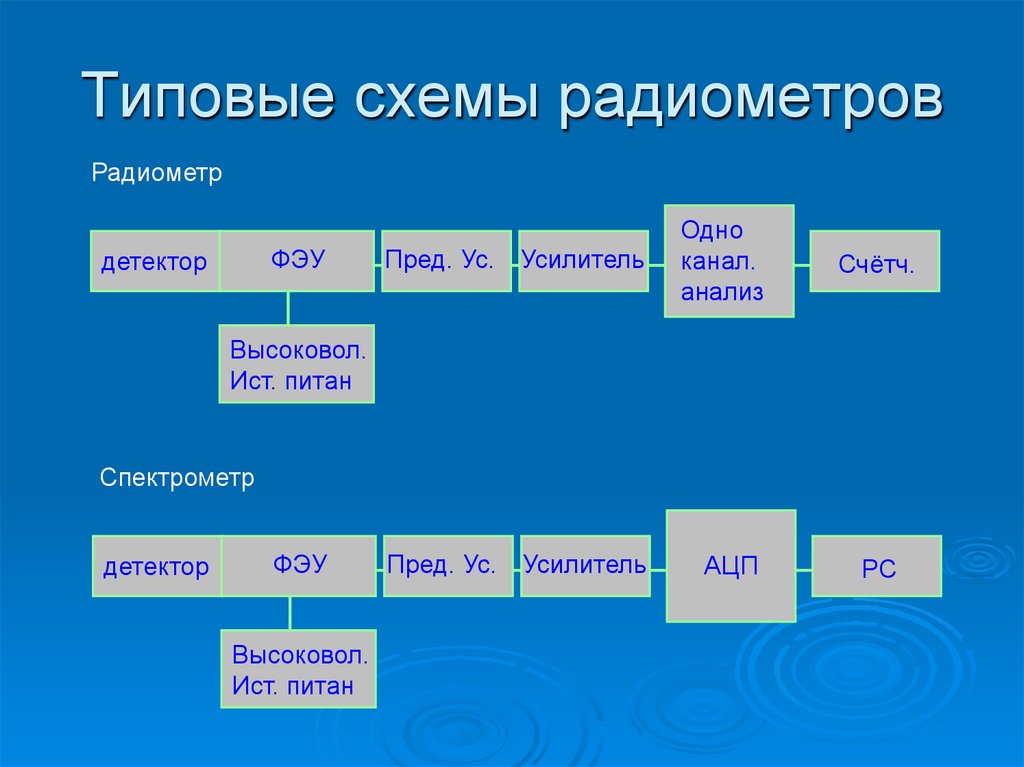
23. Типовые схемы радиометров

Радиометр
ФЭУ
детектор
Пред. Ус. Усилитель
Одно
канал.
анализ
Счётч.
Пред. Ус. Усилитель
АЦП
РС
Высоковол.
Ист. питан
Спектрометр
детектор
ФЭУ
Высоковол.
Ист. питан

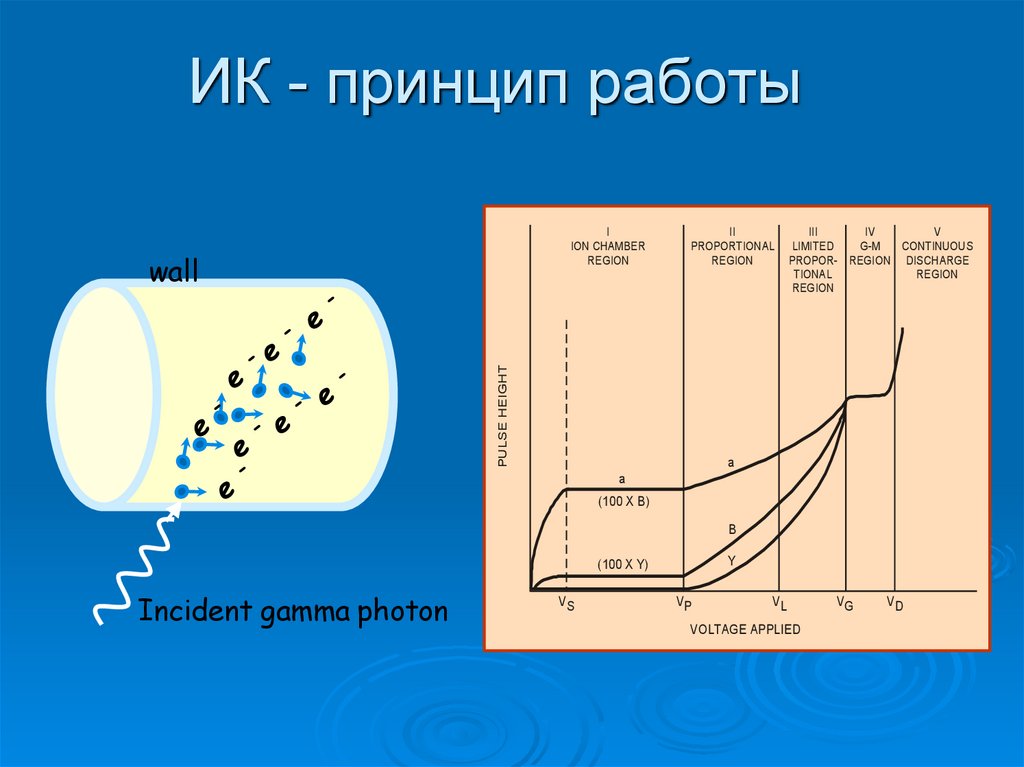
24. ИК - принцип работы

I
ION CHAMBER
REGION
PULSE HEIGHT
wall
II
PROPORTIONAL
REGION
III
IV
V
LIMITED
G-M
CONTINUOUS
PROPOR- REGION DISCHARGE
TIONAL
REGION
REGION
a
a
(100 X B)
B
Y
(100 X Y)
Incident gamma photon
VS
VP
VL
VOLTAGE APPLIED
VG
VD

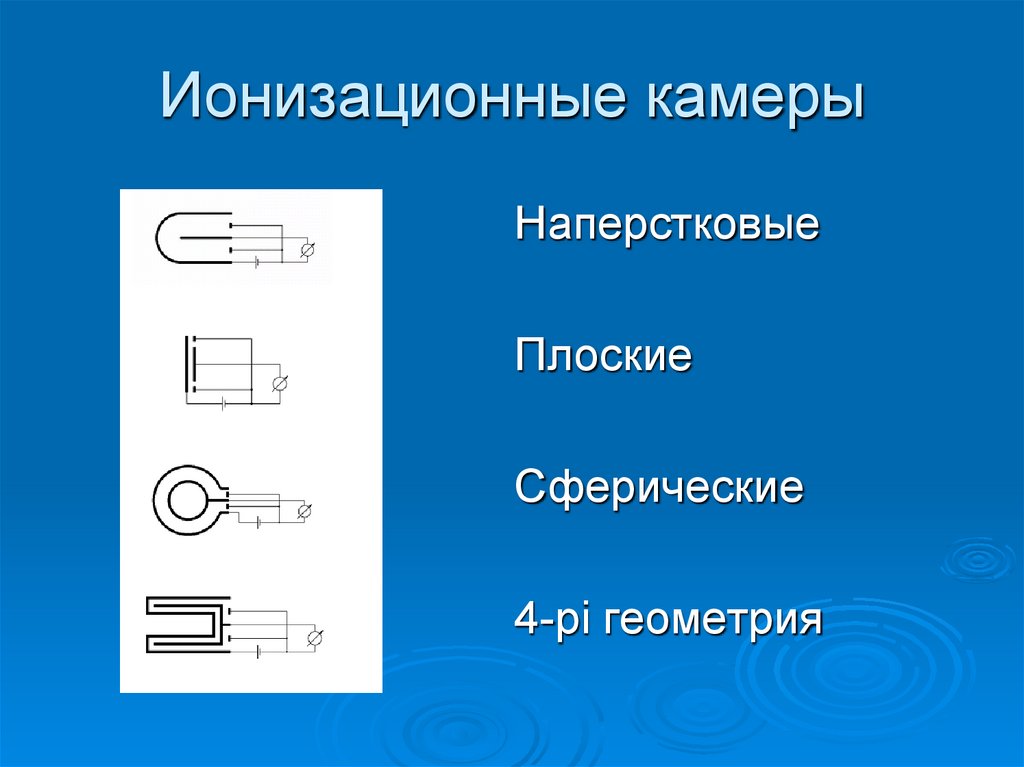
25. Ионизационные камеры

Наперстковые
Плоские
Сферические
4-pi геометрия

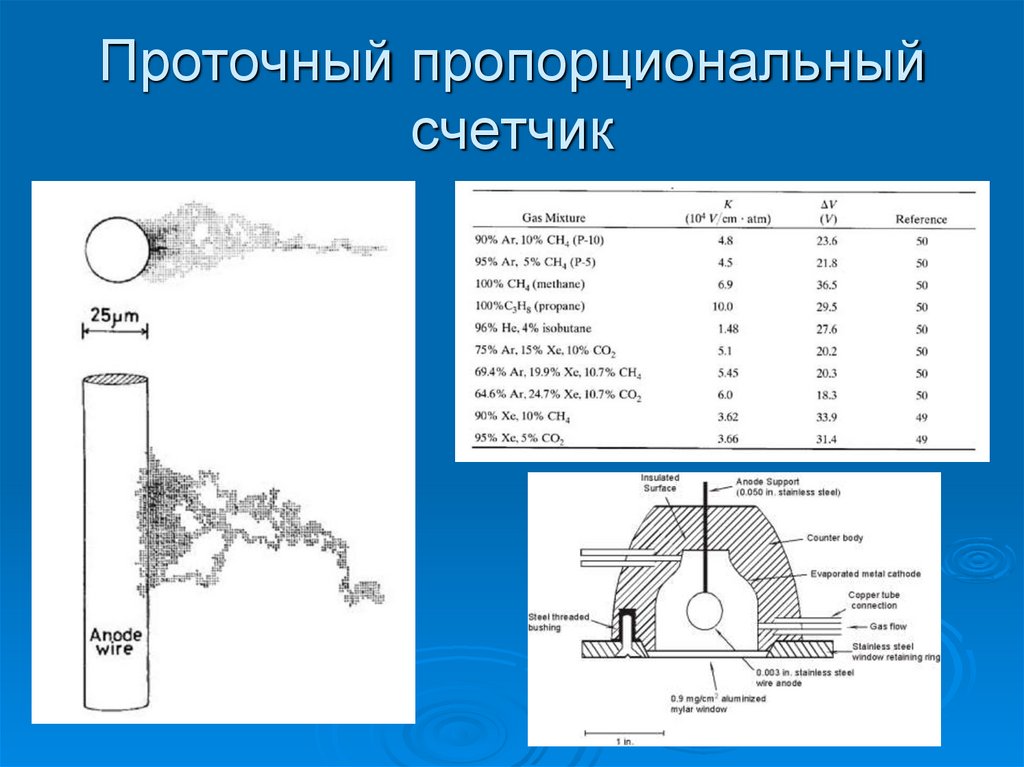
26. Проточный пропорциональный счетчик

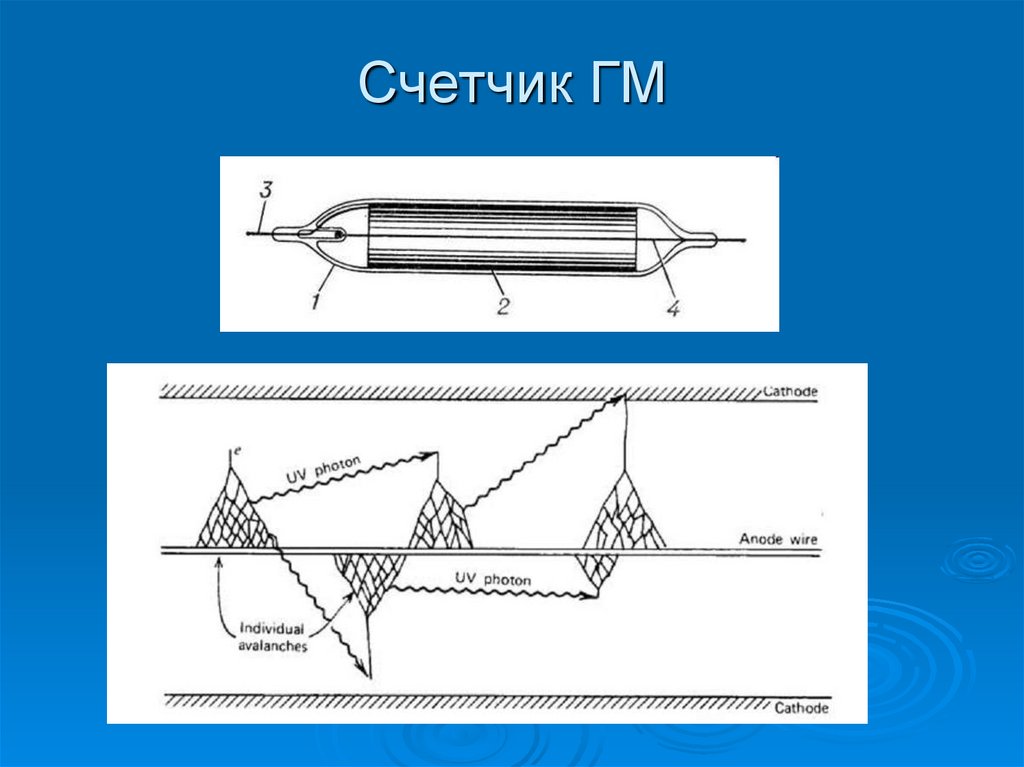
27. Счетчик ГМ

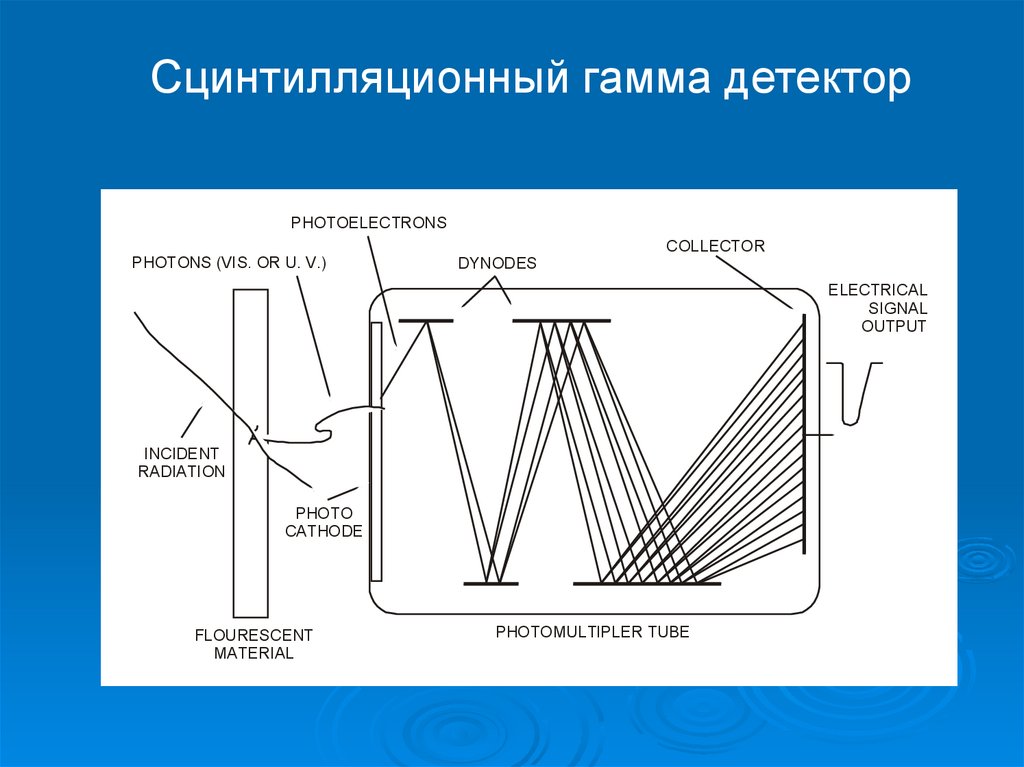
28.

Сцинтилляционный гамма детектор
PHOTOELECTRONS
COLLECTOR
PHOTONS (VIS. OR U. V.)
DYNODES
ELECTRICAL
SIGNAL
OUTPUT
INCIDENT
RADIATION
PHOTO
CATHODE
FLOURESCENT
MATERIAL
PHOTOMULTIPLER TUBE

29.

Сцинтилляционный гамма детектор
CsI(Tl)
NaI(Tl)

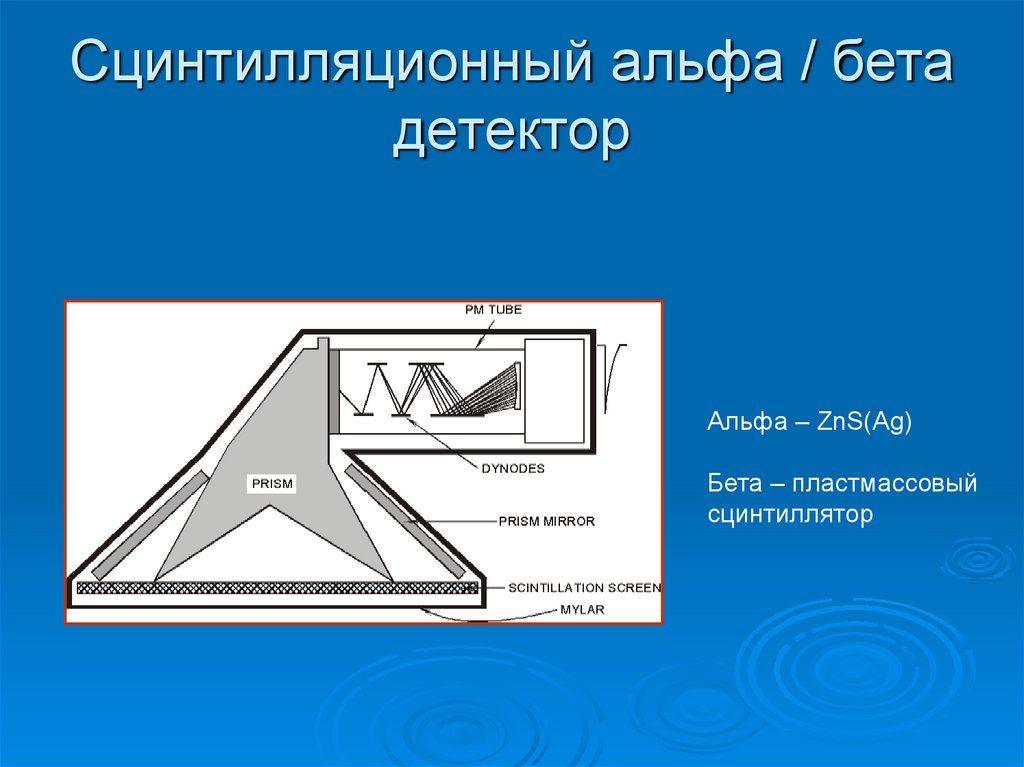
30. Сцинтилляционный альфа / бета детектор

Альфа – ZnS(Ag)
Бета – пластмассовый
сцинтиллятор

31. ЖСС

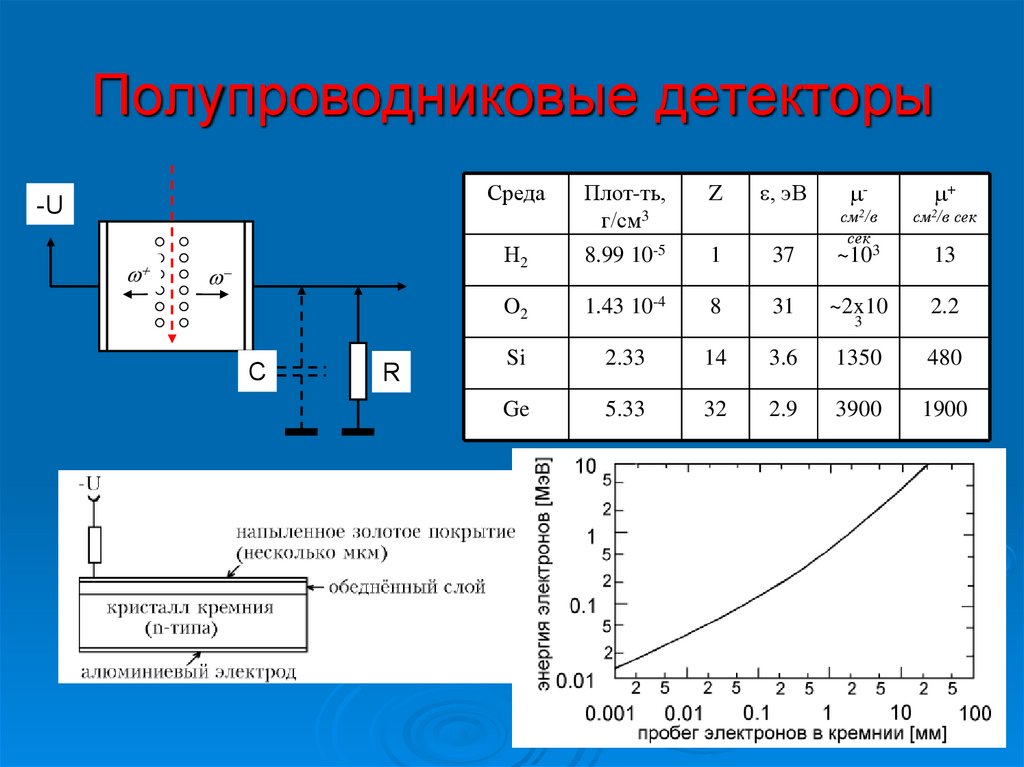
32. Полупроводниковые детекторы

Среда
-U
C
R
e, эВ
-
+
см2/в сек
37
см2/в
сек
~103
13
8
31
~2x10
2.2
2.33
14
3.6
1350
480
5.33
32
2.9
3900
1900
Z
Н2
Плот-ть,
г/см3
8.99 10-5
1
O2
1.43 10-4
Si
Ge
3

33. Полупроводниковые детекторы

Детекторы на основе сверх чистого Ge
p-i-n диод

34. Основные задачи решаемые в экологии

Измерение радиоактивности в продуктах
питания. Задачи, не требующие
пробоподготовки (А> 50 Бк/кг).
Обнаружение 137Cs на фоне 40K
Обнаружение 90Sr на фоне 137Cs и 40K

35. Обнаружение 137Cs на фоне 40K

137Cs и 40K являются бета излучателями,
однако бета распад сопровождается
гамма излучением
Позволяет использовать гамма
спектрометрию для определения
радиоактивности.

36. Спектрометрия

Спектрометрия – количественное исследование
энергетических спектров радионуклидов.
Подтверждением наличия радионуклида является
идентификация пика для этого нуклида
При выборе пиков для определения требуется чтобы:
-
-
эти пики были уникальны для данного изотопа
эти пики удовлетворительно разделяются, так что
могут быть идентифицированы
имеется достаточная статистика для обработки
этих пиков

37. - спектрометрия

- спектрометрия
Сверхчистые п/п детекторы.
Ge
CdTe
Сцинтилляторы
NaI(Tl)
CsI(Tl)

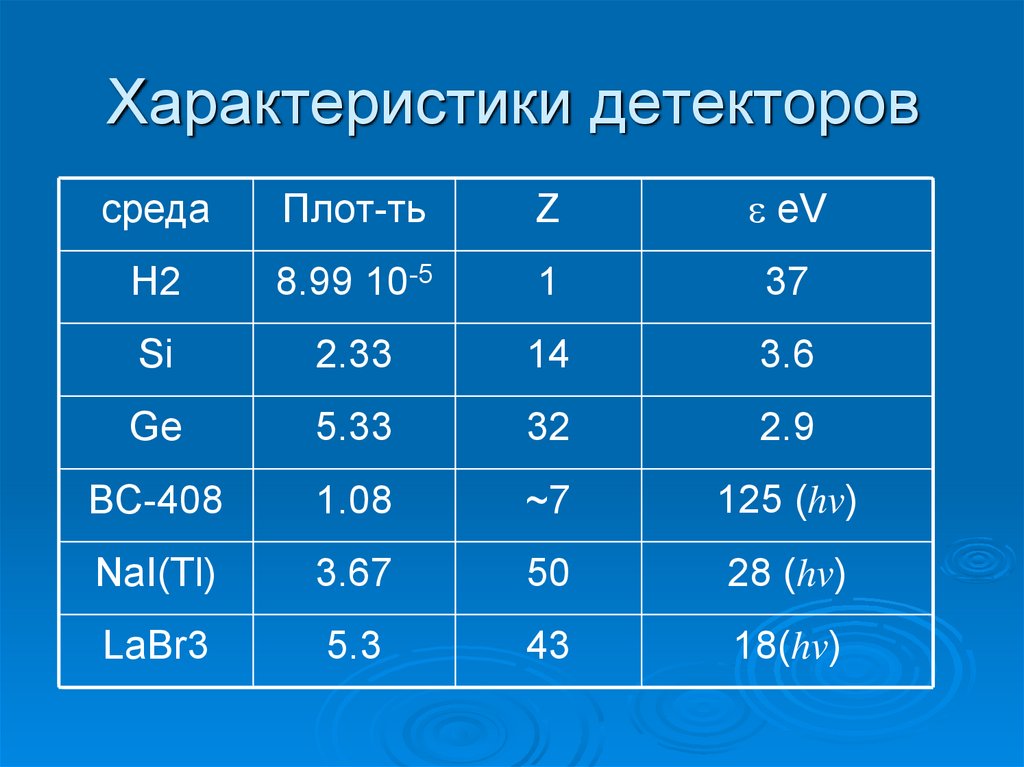
38. Характеристики детекторов

среда
Плот-ть
Z
e eV
H2
8.99 10-5
1
37
Si
2.33
14
3.6
Ge
5.33
32
2.9
BC-408
1.08
~7
125 (hv)
NaI(Tl)
3.67
50
28 (hv)
LaBr3
5.3
43
18(hv)

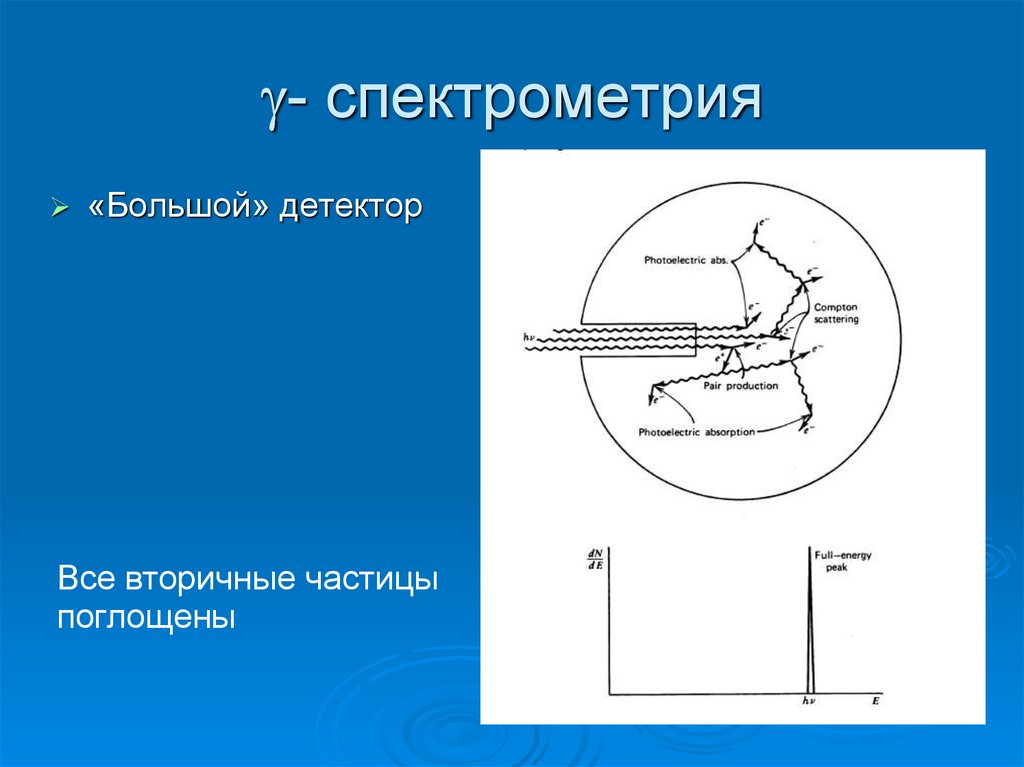
39. - спектрометрия

- спектрометрия
«Большой» детектор
Все вторичные частицы
поглощены

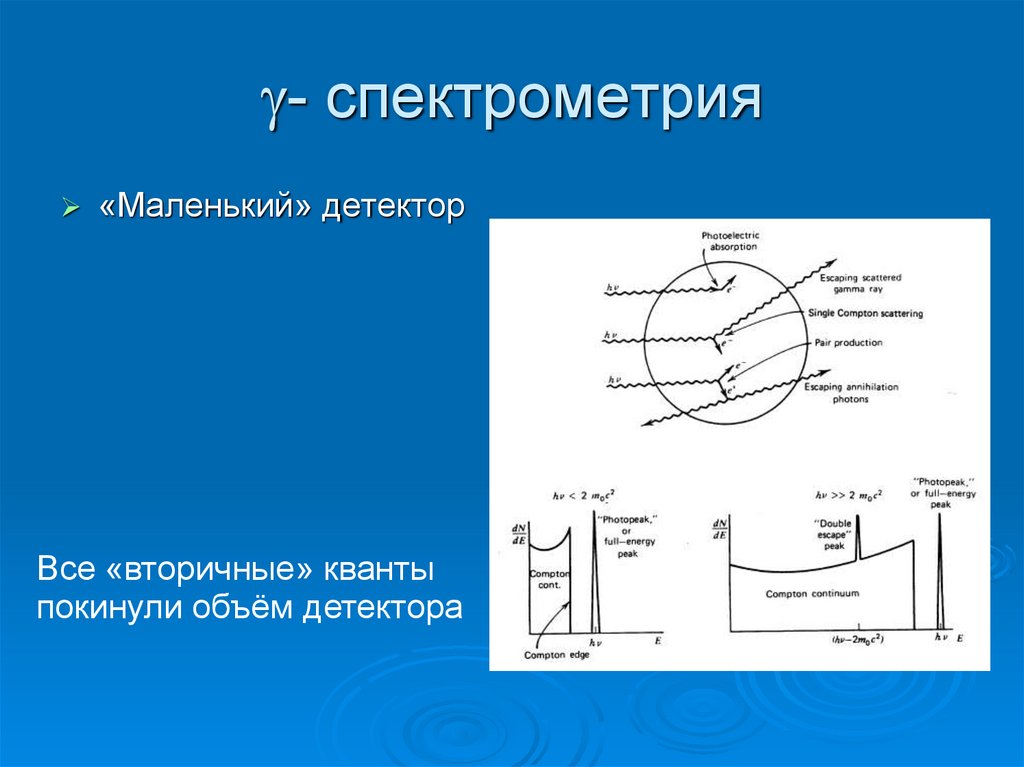
40. - спектрометрия

- спектрометрия
«Маленький» детектор
Все «вторичные» кванты
покинули объём детектора

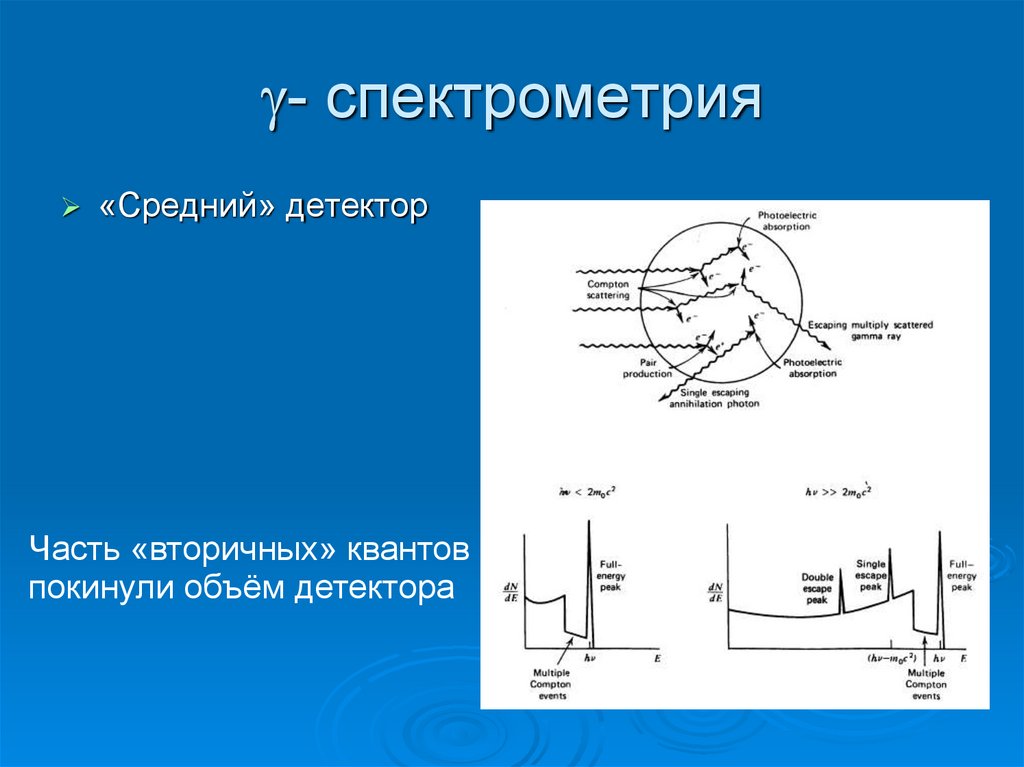
41. - спектрометрия

- спектрометрия
«Средний» детектор
Часть «вторичных» квантов
покинули объём детектора

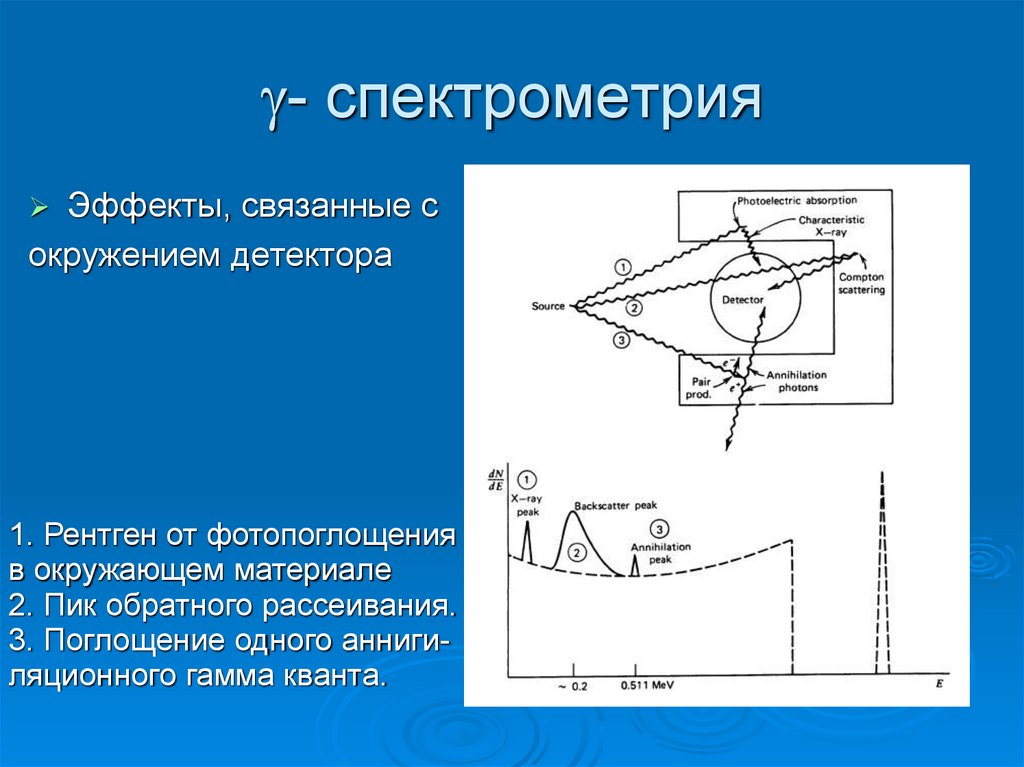
42. - спектрометрия

- спектрометрия
Эффекты, связанные с
окружением детектора
1. Рентген от фотопоглощения
в окружающем материале
2. Пик обратного рассеивания.
3. Поглощение одного аннигиляционного гамма кванта.

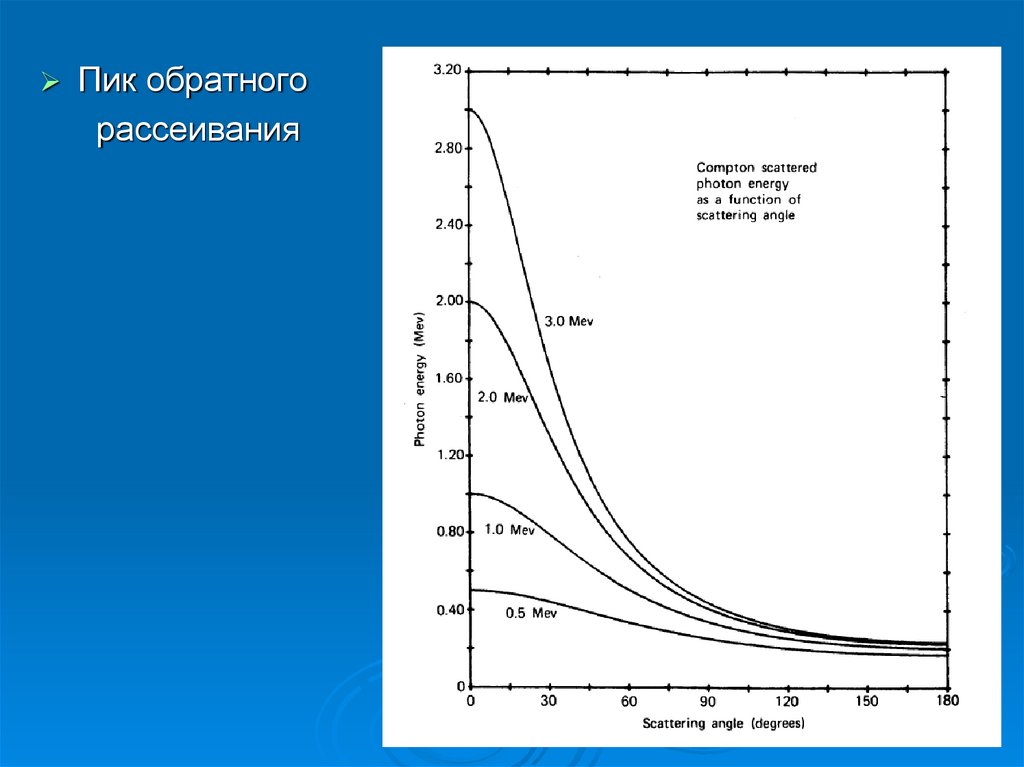
43.

Пик обратного
рассеивания

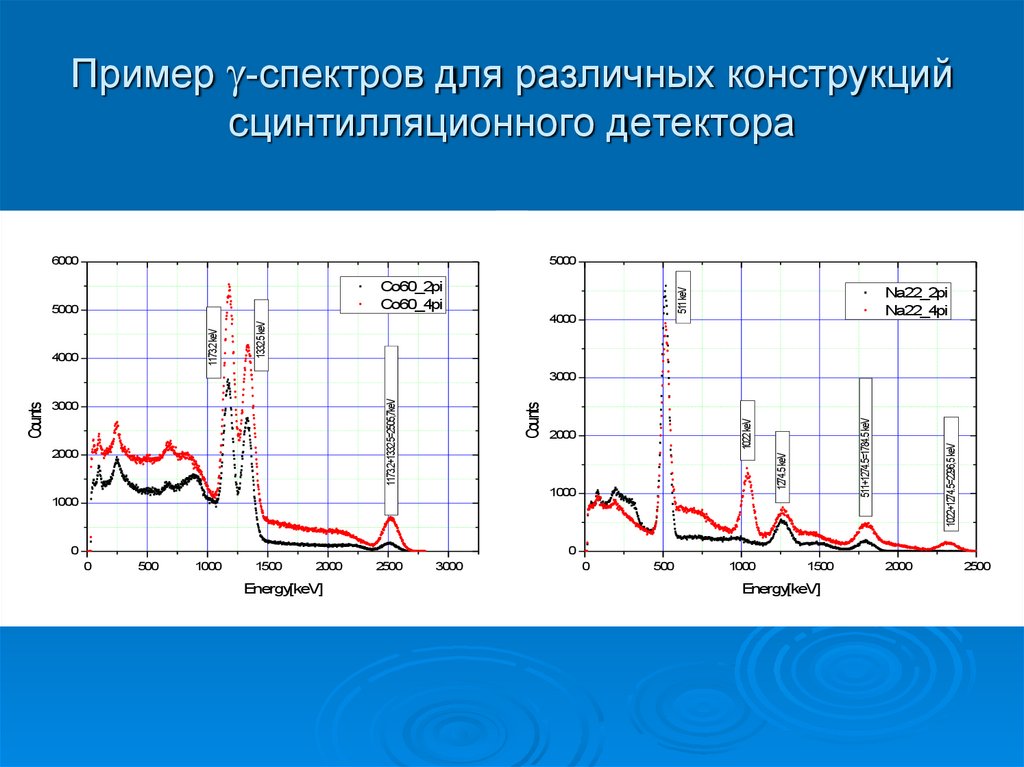
44. Пример -спектров для различных конструкций сцинтилляционного детектора

Пример -спектров для различных конструкций
сцинтилляционного детектора
6000
5000
4000
Na22_2pi
Na22_4pi
4000
1332.5 keV
1173.2 keV
5000
511 keV
Co60_2pi
Co60_4pi
0
1022+1274.5=2296,5 keV
1000
1000
511+1274.5=1784.5 keV
2000
1274.5 keV
2000
1022 keV
3000
Counts
1173.2+1332.5=2505,7keV
Counts
3000
0
0
500
1000
1500
2000
Energy[keV]
2500
3000
0
500
1000
1500
Energy[keV]
2000
2500

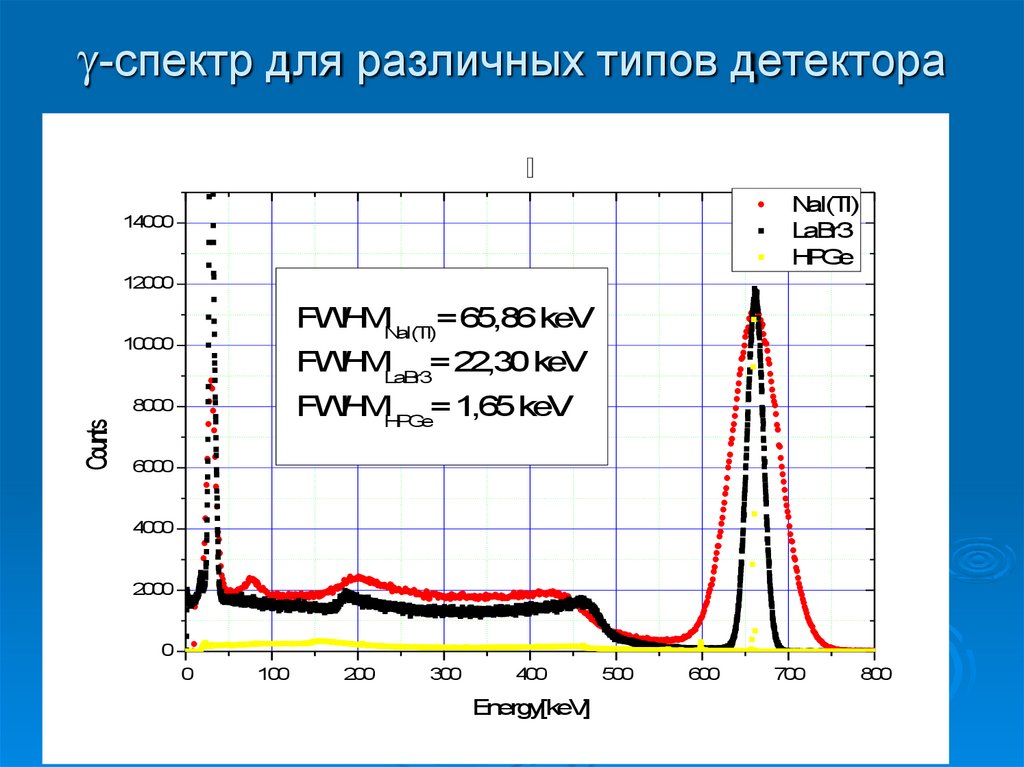
45. -спектр для различных типов детектора

-спектр для различных типов детектора
NaI(Tl)
LaBr3
HPGe
14000
12000
FWHMNaI(Tl)= 65,86 keV
10000
FWHMLaBr3= 22,30 keV
FWHMHPGe= 1,65 keV
Counts
8000
6000
4000
2000
0
0
100
200
300
400
Energy[keV]
500
600
700
800

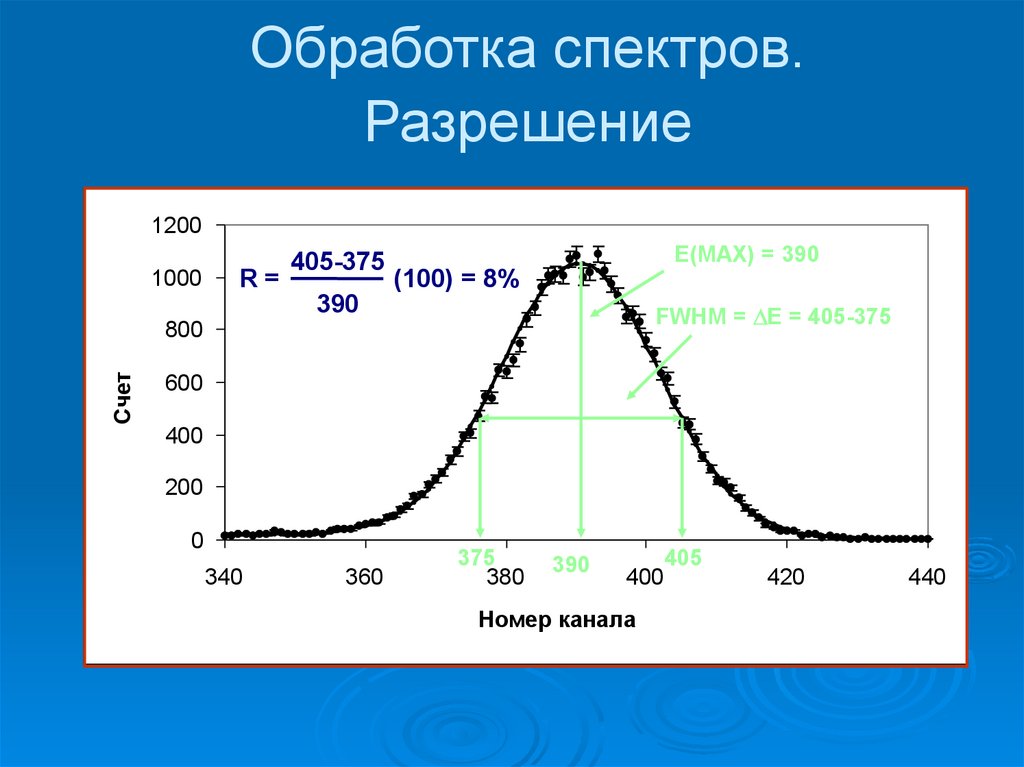
46.

Обработка спектров.
Разрешение
1200
1000
R=
405-375
E(MAX) = 390
(100) = 8%
390
FWHM = E = 405-375
Счет
800
600
400
200
0
340
360
375
380
390
400
Номер канала
405
420
440

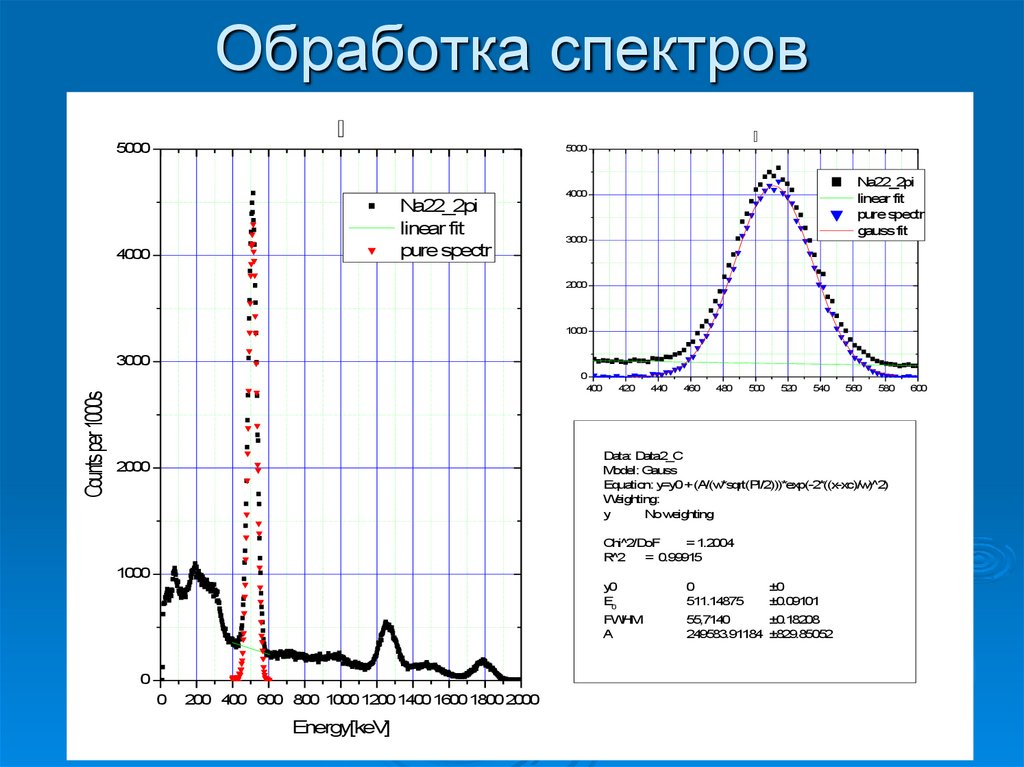
47. Обработка спектров

5000
5000
Na22_2pi
linear fit
pure spectr
gauss fit
4000
Na22_2pi
linear fit
pure spectr
4000
3000
2000
1000
Counts per 1000s
3000
0
400
420
440
460
480
500
520
540
560
580
Data: Data2_C
Model: Gauss
Equation: y=y0 + (A/(w*sqrt(PI/2)))*exp(-2*((x-xc)/w)^2)
Weighting:
y
No weighting
2000
Chi^2/DoF
= 1.2004
R^2
= 0.99915
1000
0
0
200 400 600 800 100012001400160018002000
Energy[keV]
±0
±0.09101
y0
E0
0
511.14875
FWHM
A
55,7140
±0.18208
249583.91184 ±829.85052
600

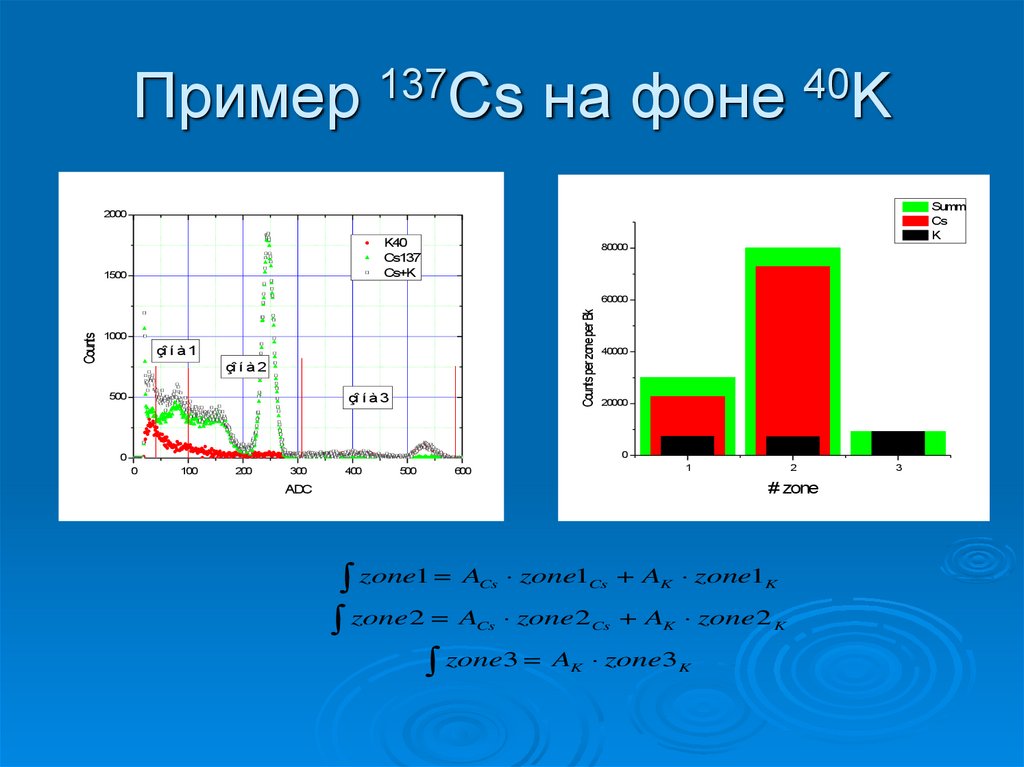
48. Матричный метод

Энергетическая шкала спектрометра
разбивается на некоторое количество не
пересекающихся зон.
Создаётся библиотека радионуклидов. (Для
каждого радионуклида считается вклад в
каждую зону матрица чувствительности).
Для спектра пробы и выбранной задачи
(состава) составляется группа уравнений
(матрица) и ищется её решение и это
решение должно иметь минимум.

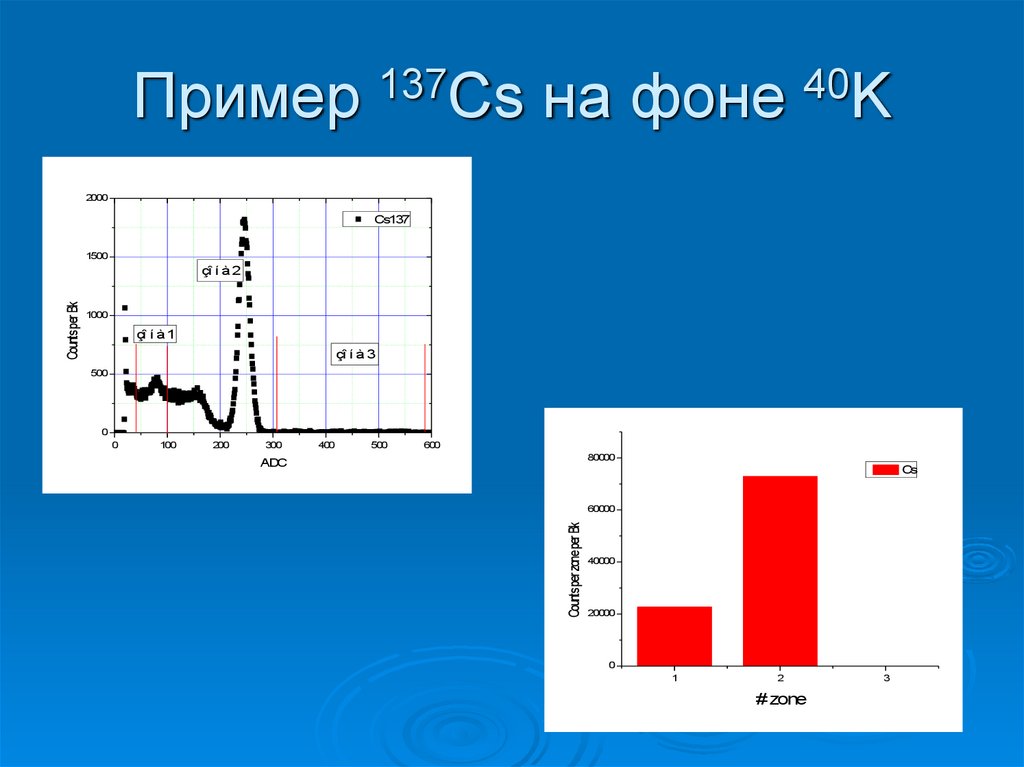
49. Пример 137Cs на фоне 40K

2000
Cs137
1500
1000
çî í à 1
çî í à 3
500
0
0
100
200
300
400
500
600
80000
ADC
Cs
60000
Counts per zone per Bk
Counts per Bk
çî í à 2
40000
20000
0
1
2
# zone
3

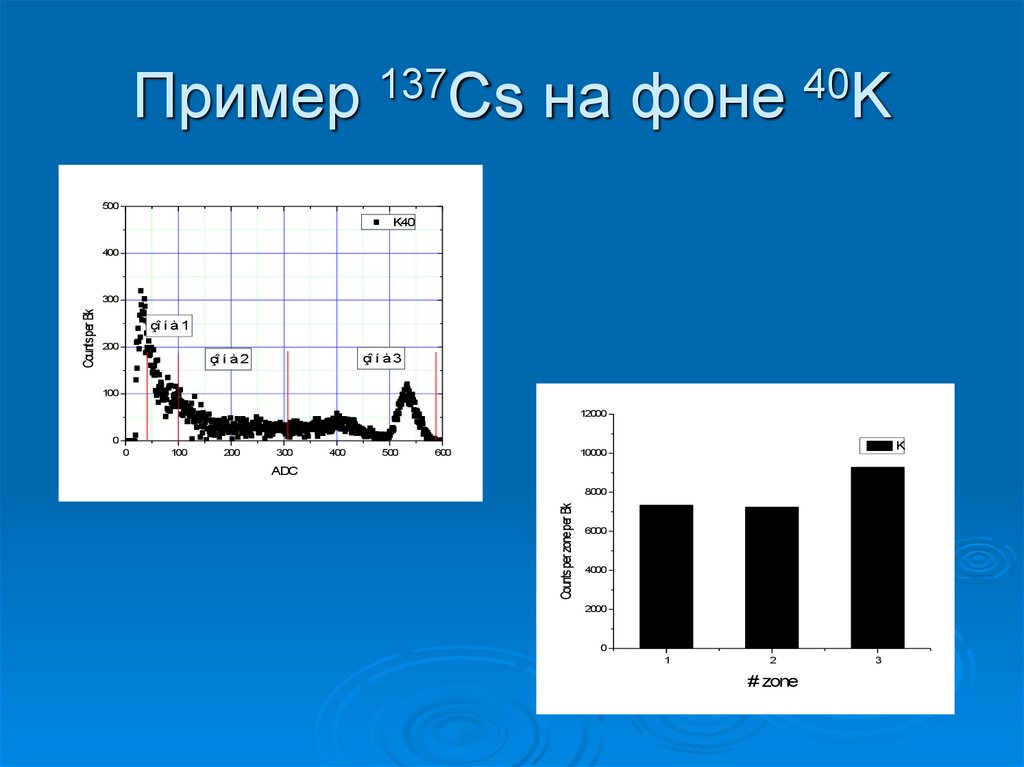
50. Пример 137Cs на фоне 40K

500
K40
400
çî í à 1
200
çî í à 3
çî í à 2
100
12000
0
0
100
200
300
400
500
K
10000
600
ADC
8000
Counts per zone per Bk
Counts per Bk
300
6000
4000
2000
0
1
2
# zone
3

51. Пример 137Cs на фоне 40K

Summ
Cs
K
2000
K40
Cs137
Cs+K
1500
80000
Counts per zone per Bk
Counts
60000
1000
çî í à 1
çî í à 2
çî í à 3
500
40000
20000
0
0
0
100
200
300
400
500
1
600
2
# zone
ADC
zone1 = A zone1 + A zone1
zone 2 = A zone 2 + A zone 2
zone3 = A zone3
Cs
Cs
K
Cs
Cs
K
K
K
K
K
3

52. Матричный метод

Простота для пользователя.
Не критичен к долговременной стабильности
спектрометрического тракта.
Не требует специальных знаний оператора.
Требует наличие библиотеки радионуклидов.
Требует энергетической калибровки.
Требует кратковременной (в пределах измерения пробы и
калибровки) стабильности спектрометрического тракта.
Требует долговременной стабильности фона.

53. Приборное обеспечение

Гамма-спектрометр с германиевым
детектором «Прогресс-гамма (ППД)»
Гамма-спектрометр со сцинтилляционным
детектором «Прогресс-гамма»

54. Существующие спектрометрические комплексы

АСПЕКТ (Дубна) + ЛСРМ (Менделеево)
АМПЛИТУДА (Зеленоград)
РАДЭК (С.-Петербург)
Зарубежные комплексы

55. АСПЕКТ + ЛСРМ

АСПЕКТ - производитель «железа».
Исторически вышли из ОИЯИ
Хорошее качество
Свое собственное производство +
зарубежные детекторы
ЛСРМ – производитель п/о
Исторически вышли из ВНИИФТРИ
Развитый аппарат, возможность решать
различные задачи, требование к
пользователю
Методическая поддержка

56. АМПЛИТУДА

«Железо».
Исторически вышли из ВНИИФТРИ
Хорошее качество
Свое собственное производство +
зарубежные детекторы
п/о
Узкая направленность на конкретные
задачи.
Методическая поддержка

57. РАДЭК

«Железо».
Исторически вышли из ВНИИМ
Хорошее качество
Свое собственное производство +
зарубежные детекторы
п/о
Требует доработки
Методическая поддержка

58. Зарубежные комплексы

«Железо».
В основном только детекторы
Качество
Защита
п/о
Требует доработки до наших реалий
Методическая поддержка

59. Обнаружение 90Sr на фоне 137Cs и 40K

Распад 90Sr не сопровождается гамма излучением.
Гамма спектрометрия не подходит для его
идентификации
Необходима бета спектрометрия/радиометрия
90Sr(E
90Y(E
=0,546
MeV)
max
max=2.238 MeV)
40K(E
max=1,311 MeV)

60. - спектрометрия

- спектрометрия
Проточные пропорциональные
счетчики, пропорциональные счетчики.
p-i-n диоды (менее 500 кеВ).
Сцинтилляторы
Пластмассовые (зависит от выбранной
толщины, 1 см достаточно для поглощения
~ 2 МэВ электрона)
ЖСС (нет возможности работы в нативе)
«тяжелые» сцинтилляторы не подходят.

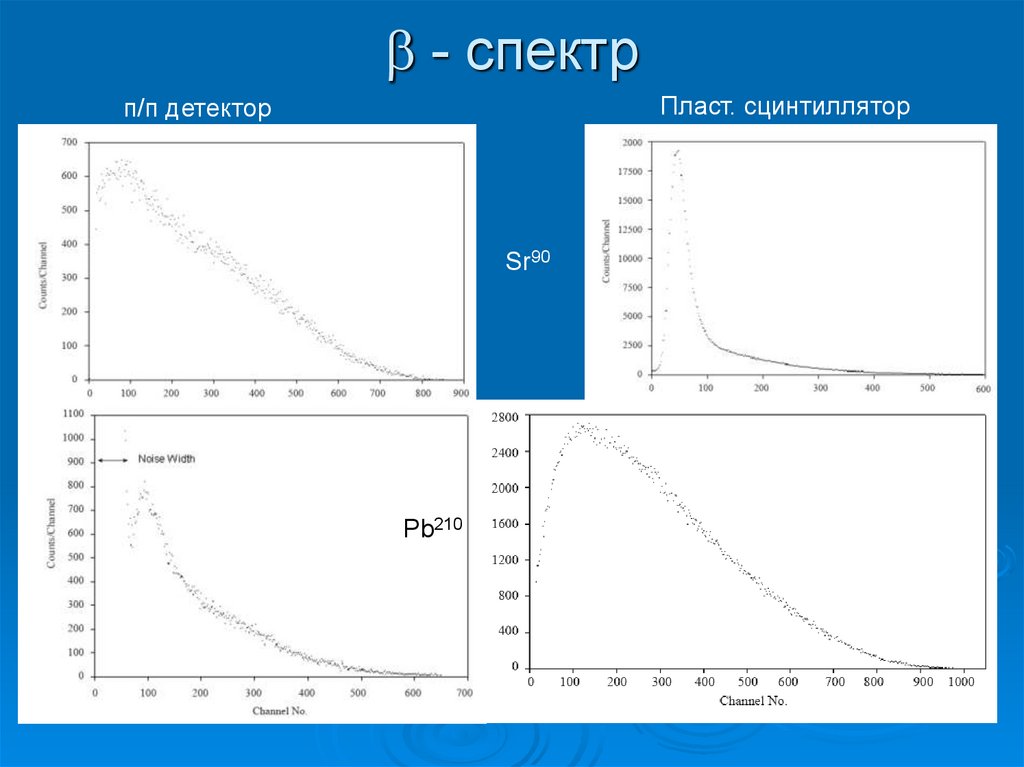
61. - спектр

- спектр
Пласт. сцинтиллятор
п/п детектор
Sr90
Pb210

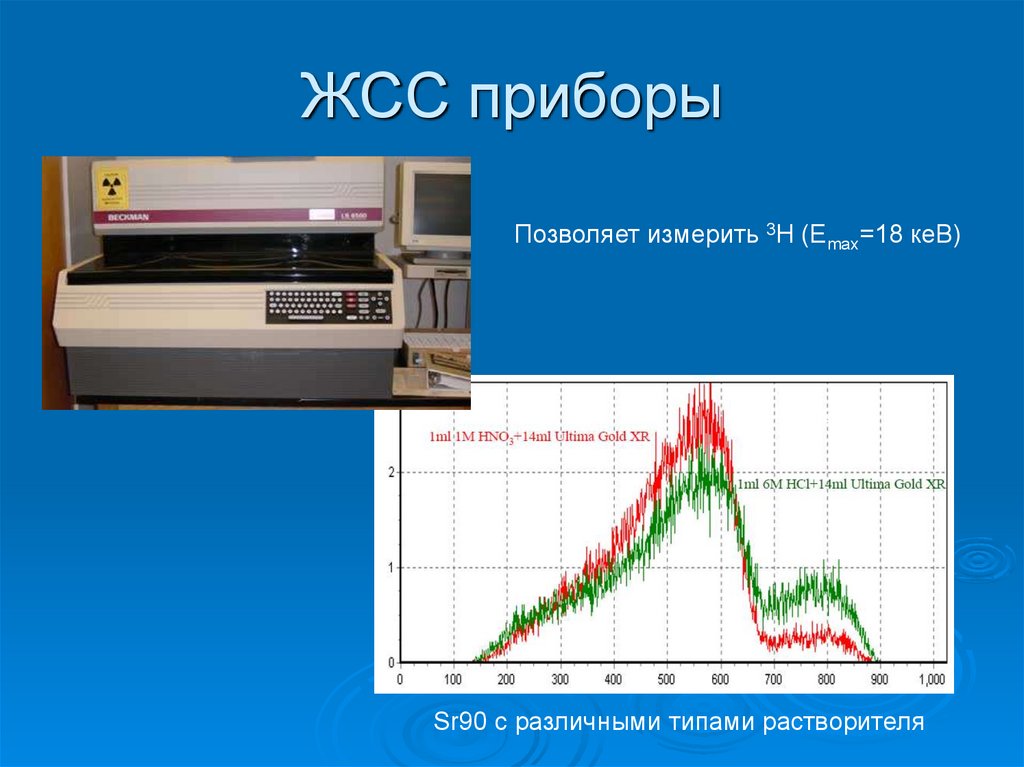
62. ЖСС приборы

Позволяет измерить 3Н (Emax=18 кеВ)
Гашение
Sr90 c различными типами растворителя

63. Сцинтилляционные приборы

64. Основные ошибки

Несоблюдение геометрии измерения
Нарушение регламента работы:
Отсутствие регулярной энергетической
калибровки
Отсутствие регулярных измерений фона

65. Задача - измерение в стройматериалах

Измерение 40К, 226Ra с дочерними
продуктами и 232Th с дочерними продуктами в
стройматериалах. Задача аналогична
рассмотренной выше, но требуется
дополнительно измерить 226Ra с дочерними
продуктами и 232Th, которые успешно
измеряются используя гамма спектрометрию.
Основная ошибка, возникающая при этих
измерениях, это нарушение регламента
измерения (без выдержки 10 суток в
закрытом объёме)

66. Основные задачи, решаемые в экологии (малая активность)

Измерение радиоактивности в воде и воздухе.
Задачи, требующие пробоподготовки.
Пример: вода
Суммарная бета активность менее 1 Бк/л
Суммарная альфа активность менее 0.2 Бк/л

67. Измерение малых активностей

Проверка установки на предмет постоянства фона.
Измерение фона должно происходить по возможности в тех
же условиях, что и измерение пробы.
Результаты измерения фона должны подвергаться
статистическому анализу.
В некоторых случаях измерение пробы может повлиять на
последующие значения фона установки.
Проверка стабильности установки
При проведении измерения пробы необходимо быть
уверенным, что установка не меняет своих характеристик
При проведении измерения пробы необходимо быть
уверенным, что проба не меняет своих характеристик

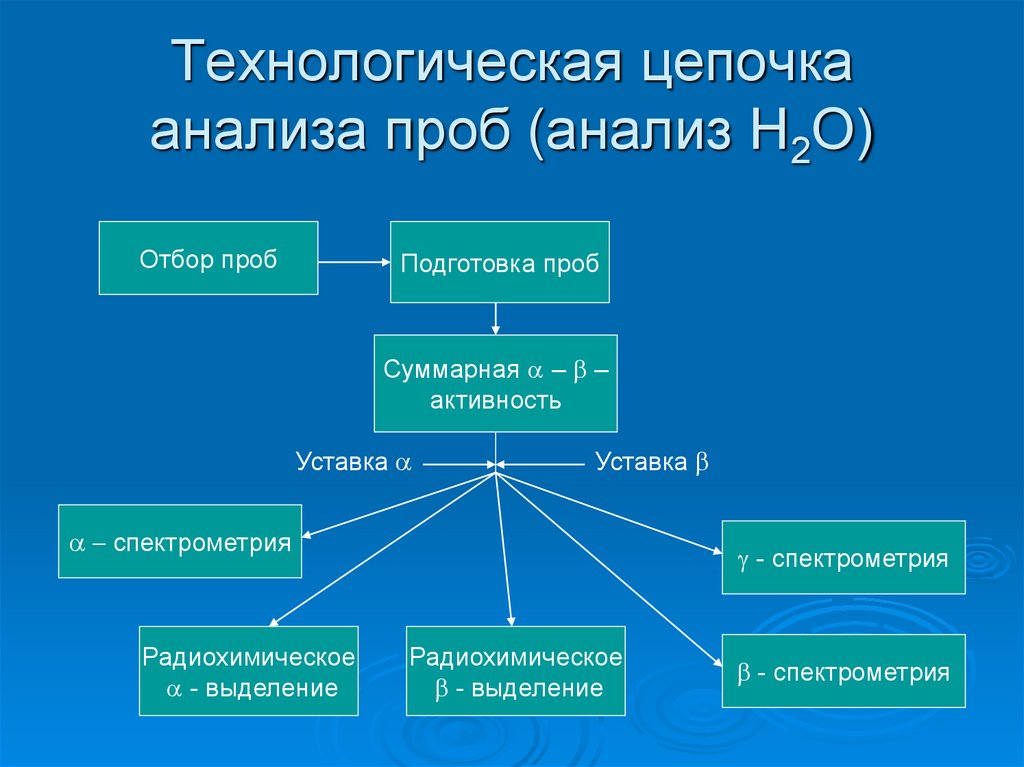
68. Технологическая цепочка анализа проб (анализ Н2О)

Отбор проб
Подготовка проб
Суммарная a – –
активность
Уставка a
Уставка
a спектрометрия
Радиохимическое
a - выделение
- спектрометрия
Радиохимическое
- выделение
- спектрометрия

69. - спектрометрия

a- спектрометрия
Проточные пропорциональные счетчики и
пропорциональные счетчики с тонким окном.
Кремниевые диоды.
с использованием вакуумной камеры;
без использования вакуумной камеры.
Сцинтилляторы
Пластические
ЖСС
Тонкий CsI(Tl)

70.

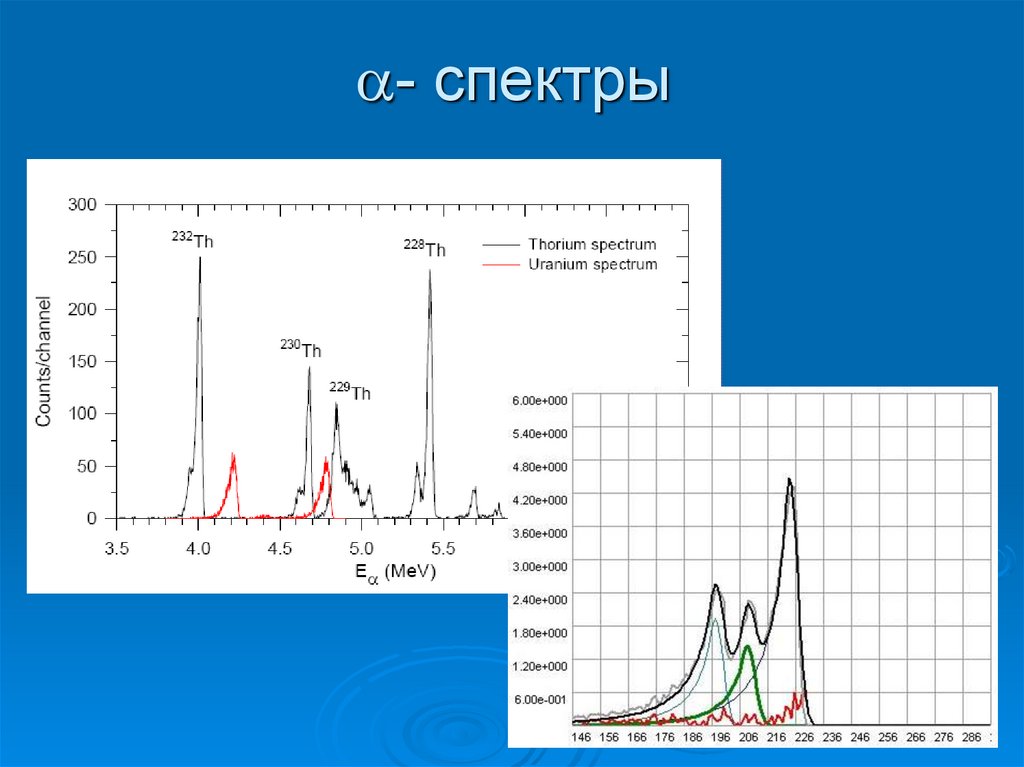
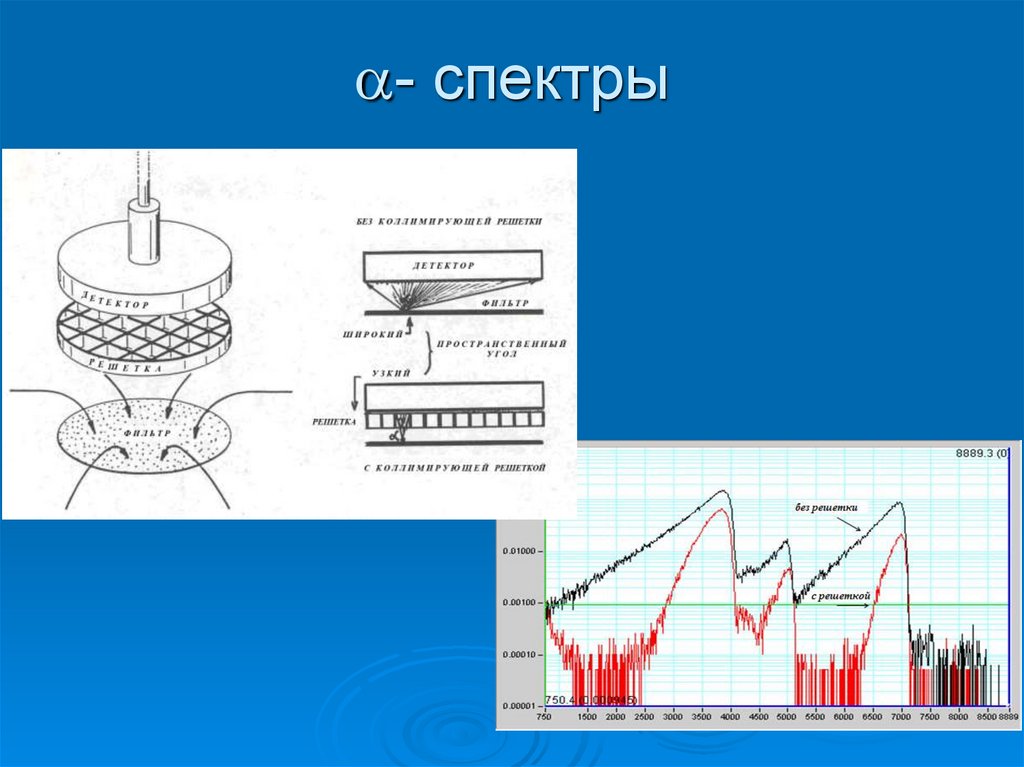
a- спектры

71. - спектры

a- спектры

72. Приборное обеспечение

Альфа-спектрометр Прогресс
(Мультирад)
Радиометр УМФ-2000

73. Измерение плотности потока

Сцинтилляционный:
Альфа – ZnS(Ag)
Бета – пластмассовый
Сцинтиллятор

74. Измерение плотности потока

Альфа/Бета детекторы
Бета детекторы

75. Измерения в медицине

4 pi геометрия
Высокая
стабильность < 1% /
год
Чувствительность
65fA/МБк (I-125)

76. Статистка отсчета

Радиоактивный
процессом.
распад
является
случайным
Следовательно, любое измерение, основанное на
наблюдении излучения, испускаемого во время
ядерного распада, подвержено статистической
флуктуации.
Эти
собственные
флуктуации
представляют
неустранимый источник неопределенности во всех
ядерных измерениях.

77. Статистка отсчета

Понятие
статистики отсчета служит основой
статистического
анализа,
необходимого
для
обработки результатов экспериментального счета
частиц.
Статистика отсчета используется для предсказания
ожидаемой неопределенности этих измерений.

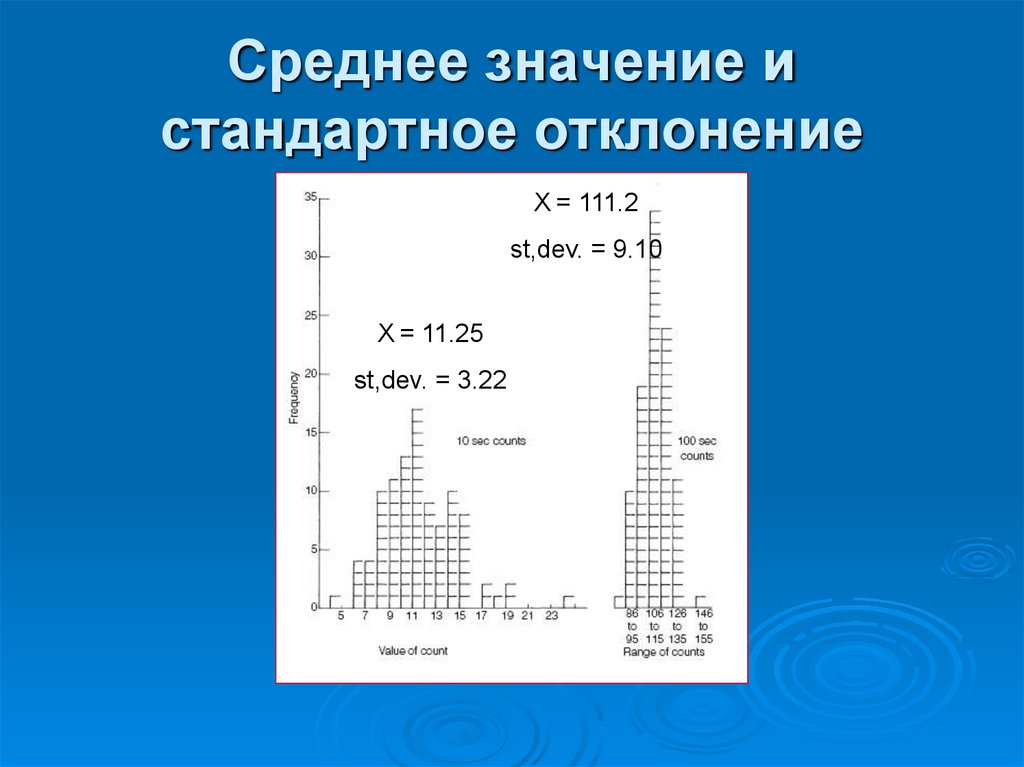
78. Среднее значение и стандартное отклонение

10-секундные отсчеты x 100
100-секундные отсчеты x 100
7 9 11 13 9 13 13 9 11 11
11 6 11 15 15 8 9 13 12 10
19 18 11 9 12 9 12 10 10 12
12 10 11 17 8 15 11 15 24 15
7 8 14 12 11 15 14 11 10
4 11 8 8 9 13 8 15 11 6
11 17 14 14 14 8 12 8 10
10 9 15 12 12 9 14 19 9 14
6 6 13 11 11 8 14 10 10 10
10 14 7 7 9 11 13 11 14 10
120 92 108 107 117 98 146 117 112 92
131 86 90 109 112 119 123 88 101 112
127 104 85 111 99 114 118 133 127 107
96 115 118 113 120 119 109 97 110 94
114 123 114 123 97 121 80 98 108 126
97 131 97 105 125 93 120 112 115 118
130 121 111 110 114 114 101 117 109 122
113 108 106 128 122 100 90 126 111 94
115 104 119 105 102 103 98 105 120 108
116 123 130 109 110 107 112 122 109 131

79. Среднее значение и стандартное отклонение

X = 111.2
st,dev. = 9.10
X = 11.25
st,dev. = 3.22

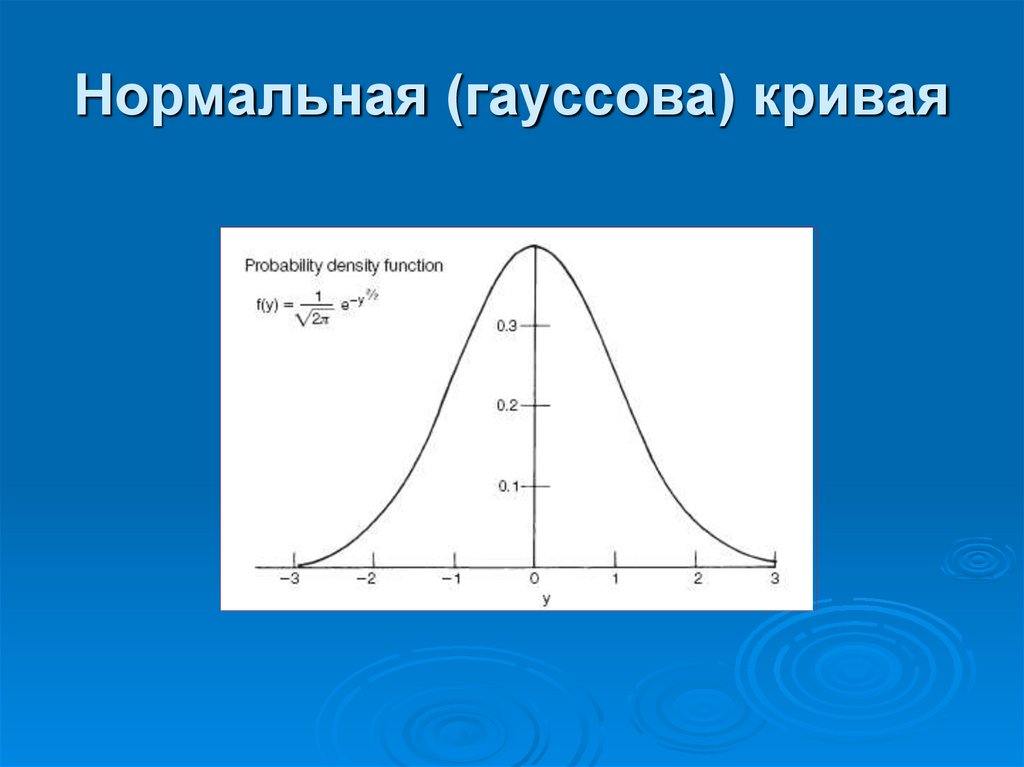
80. Нормальная (гауссова) кривая

Ряд измерений, являющихся результатом
многочисленных случайных влияющих факторов
распределены по нормальному закону. Для
построения этой кривой достаточно два параметра
— среднее значение и стандартное отклонение.
Стандартное отклонение - это характеристика
нормального распределения, когда 68 % значений
попадает в пределы одного стандартного отклонения
от среднего значения, 95 % в пределы 1,96
стандартных отклонений, и 99 % в пределы 2,58
стандартных отклонений.

81. Нормальная (гауссова) кривая

82. Нормальная (гауссова) кривая

Гистограмма повторяющихся отсчетов в течение 100
секунд счета вполне соответствует нормальной
кривой.
На гистограмме для 10 секунд счета наблюдается
отчетливая асимметрия, и при замене ее на
симметричную нормальную кривую вносится
некоторая погрешность.
Асимметрия становится более отчетливой при
уменьшении среднего значения. В результате
изменчивость при повторяющихся отсчетах
подчиняется скорее закону распределения
Пуассона, чем закону нормального распределения.

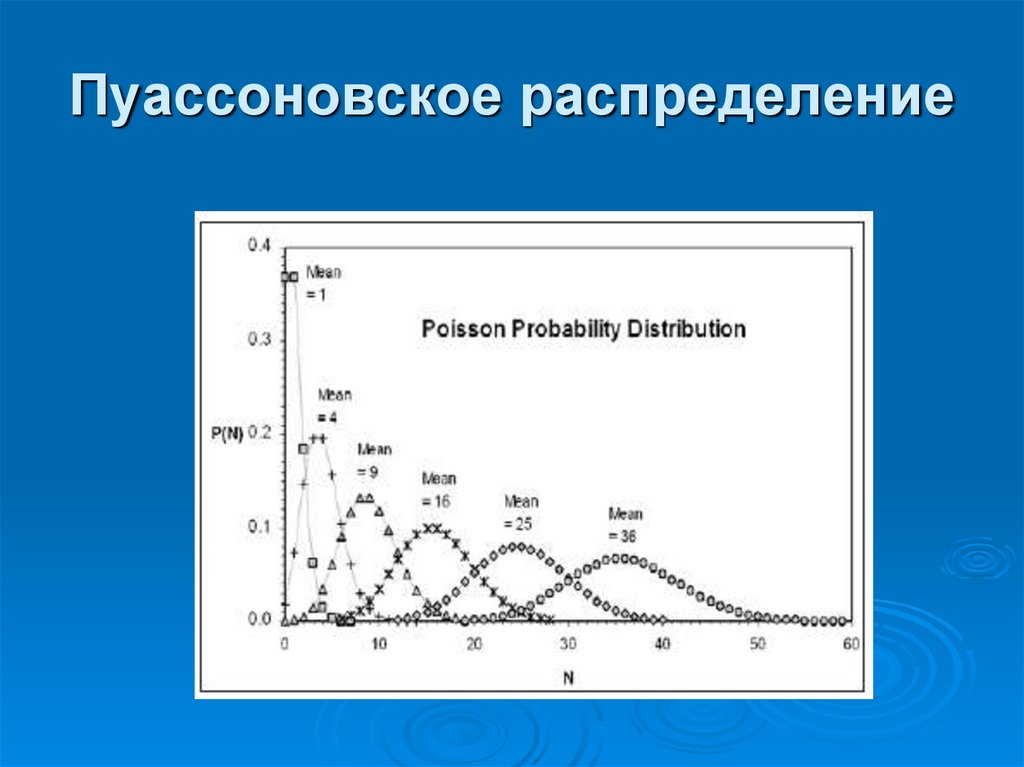
83. Пуассоновское распределение

Несмотря на то, что пуассоновское распределение
для небольшого числа событий (менее 16)
ассимметрично, с увеличением числа событий оно
быстро принимает форму нормального
распределения.
Особенностью пуассоновского распределения
является то, что среднее значение равно квадрату
стандартного отклонения.
Таким образом, нормальную кривую, подходящую
данным, можно получить, имея только один
параметр – арифметическое среднее значение.
Стандартное отклонение получается просто
извлечением корня квадратного из среднего
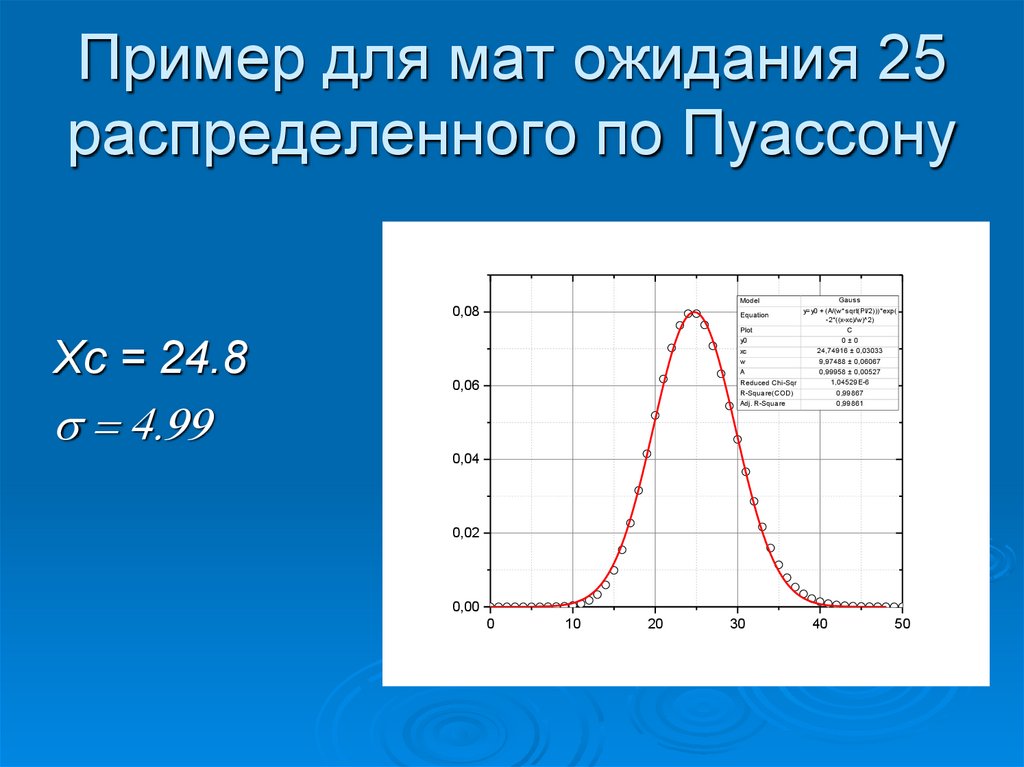
значения.

84. Пуассоновское распределение

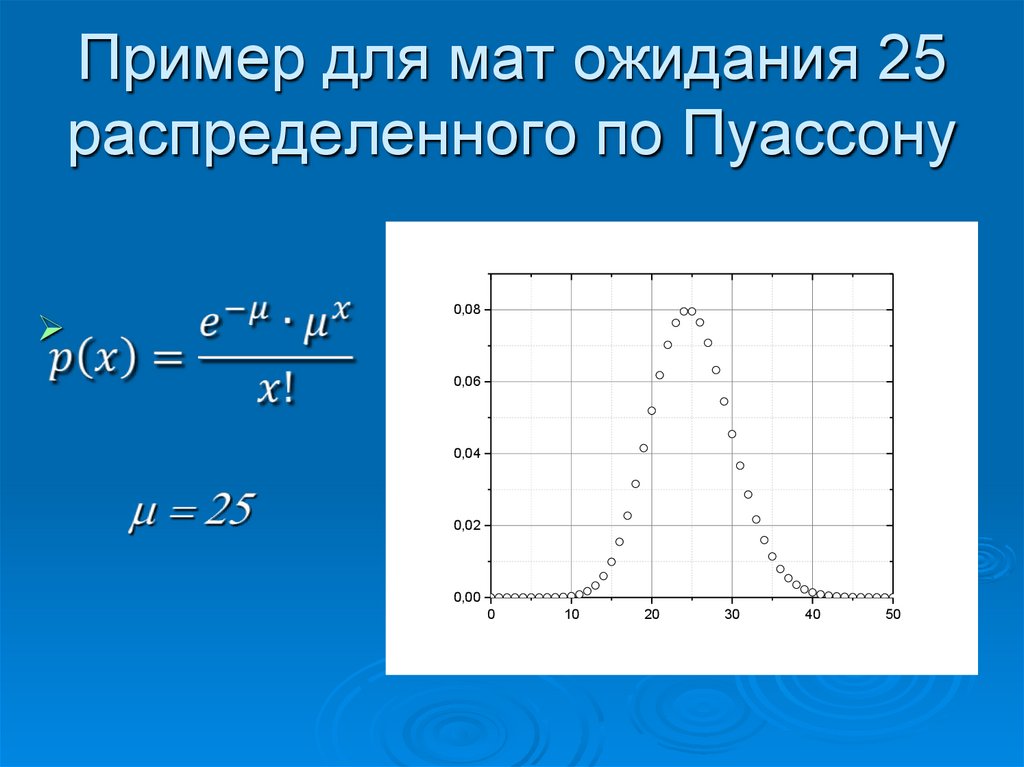
85. Пример для мат ожидания 25 распределенного по Пуассону

0,08
0,06
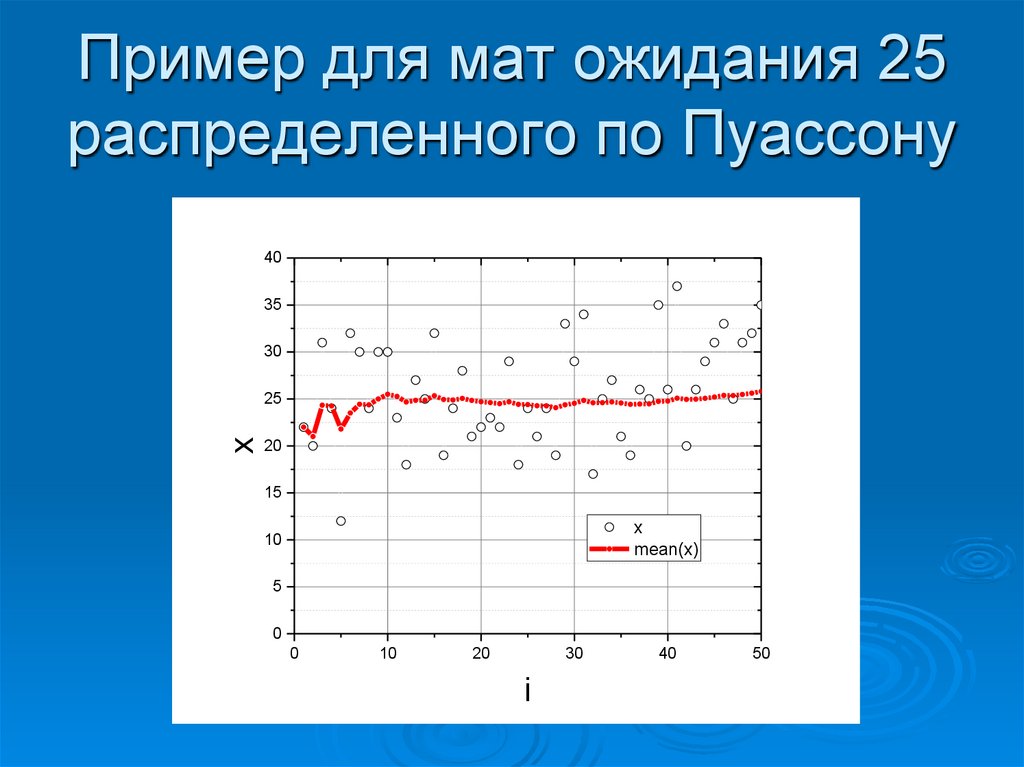
0,04
0,02
0,00
0
10
20
30
40
50

86. Пример для мат ожидания 25 распределенного по Пуассону

Gaus s
Model
0,08
Equation
Plot
Xc = 24.8
s 4.99
0,06
y=y0 + (A/(w*s qrt(PI/2)))*exp(
-2*((x-xc)/w)^2)
C
y0
0±0
xc
24,74916 ± 0,03033
w
9,97488 ± 0,06067
A
0,99958 ± 0,00527
Reduced Chi-Sqr
1,04529E-6
R-Square(COD)
0,99867
Adj. R-Square
0,99861
0,04
0,02
0,00
0
10
20
30
40
50

87. Пример для мат ожидания 25 распределенного по Пуассону

x
p(x)
x
p(x)
x
p(x)
x
p(x)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
1,39E-11 3,47E-10 4,34E-09 3,62E-08 2,26E-07 1,13E-06 4,71E-06 1,68E-05 5,256E-05 1,46E-04 3,65E-04
8,30E-04 1,73E-03 3,32E-03
2,28E+03 91,33
7,31
10,67
1,71
10,24
2,46
16,52
5,29
1,90
2 739,84
1 205,53
578,65
300,90
лет
месяц
день
час
секунд
14
15
16
17
18
19
20
21
22
23
24
25
26
27
0,005935 0,009891 0,015455 0,022727 0,031566 0,041534 0,051917 0,061807 0,0702347 0,076342 0,07952295 0,07952295 0,0764644 0,07080035
168,50
101,10
64,71
44,00
31,68
24,08
19,26
16,18
14,24
13,10
12,57
12,57
13,08
14,12
секунд
28
29
30
31
32
33
34
35
36
37
38
39
40
41
0,063215 0,054495 0,045413 0,036623 0,028612 0,021676 0,015938 0,011384 0,0079058 0,0053417 0,00351429 0,00225275 0,001408 0,00085852
15,82
18,35
22,02
27,31
34,95
46,13
62,74
87,84
126,49
187,21
284,55
443,90
710,24
1 164,80
секунд
42
43
44
45
46
47
48
49
50
51
52
53
54
55
0,000511 0,000297 0,000169 9,38E-05 5,1E-05 2,71E-05 1,41E-05 7,2E-06 3,602E-06 1,766E-06 8,4893E-07 4,0044E-07 1,854E-07 8,4267E-08
1,96E+03
0,93
1,65
2,96
5,45
10,25
19,67
1,61
3,21
6,55
13,63
28,90
2,08
4,58
секунд
час
день
месяц

88. Пример для мат ожидания 25 распределенного по Пуассону

20
28
27
14
25
36
19
34
24
0,051917
0,063215
0,0708
0,005935
0,079523
0,007906
0,041534
0,015938
0,079523
24
100
0,07952295 9,2605E-30
Среднее (1-11) = 31.9; СКО (1-11) = 23.4
Среднее (1-10) = 25.1; СКО (1-10) = 6.66
25
25
25
25
25
25
25
25
25
25
25
0,079523
0,079523
0,079523
0,079523
0,079523
0,079523
0,079523
0,079523
0,079523
0,079523
0,079523
Среднее (1-11) = 25; СКО (1-11) = 0
P(25)=0,0795; P(25&25) = P(25)*P(25) = 0.0795*0.0795 =0,00632

89. Пример для мат ожидания 25 распределенного по Пуассону

40
35
30
x
25
20
15
x
mean(x)
10
5
0
0
10
20
30
i
40
50

90. Точность единичного измерения

интерпретации реальных результатов
Что означает “единичное измерение”? Количество
отсчетов, определяемое во время измерения, может
составлять несколько тысяч, если проба довольно
активная, или это может быть всего несколько
отсчетов в случае измерения низкой активности.
Какое значение имеет полученное число?

91. Точность единичного измерения

Полученное число является лучшей оценкой
среднего значения, которые мы получили бы, если
бы мы могли выполнить множество повторяющихся
измерений.
Оно действительно самое лучшее, поскольку у нас
нет других измерений.
Однако истинное среднее значение, скорее всего,
отличается от результата нашего измерения, но мы
можем установить пределы, в которые, вероятно,
попадает истинное среднее значение.

92. Точность единичного измерения

Вероятность, что истинное среднее значение
находится в заданных пределах измеренного
значения, определяется по нормальной кривой,
полученной при среднем значении, равном
измеренному количеству импульсов (N), и
стандартном отклонении (s), равном корню
квадратному из измеренного количества отсчетов:
s N

93. Точность единичного измерения

68 % вероятности, что истинное среднее значение
находится в интервале между N + √N и N − √ N.
95 % вероятности, что истинное среднее значение
находится в интервале между N+1,96 √N и N−1,96 √
N.
99 % вероятности, что истинное среднее значение
находится в интервале между N + 2,58 √N и N −2,58 √
N.

94. Точность единичного измерения (большое число)

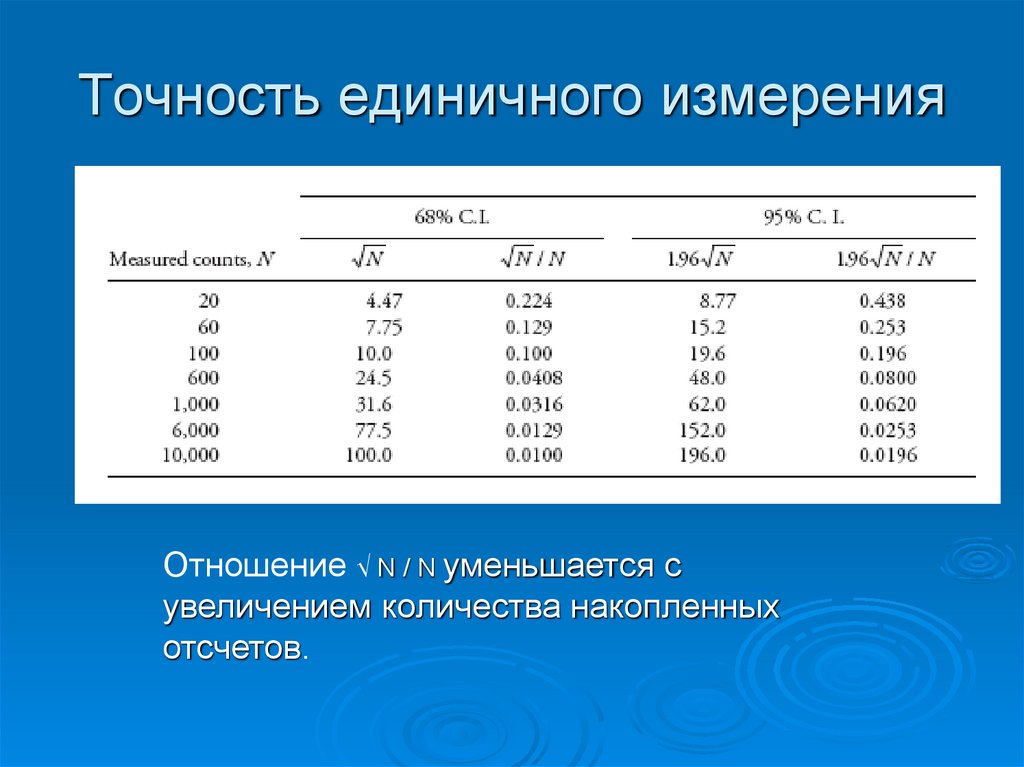
95. Точность единичного измерения

Отношение √ N / N уменьшается с
увеличением количества накопленных
отсчетов.

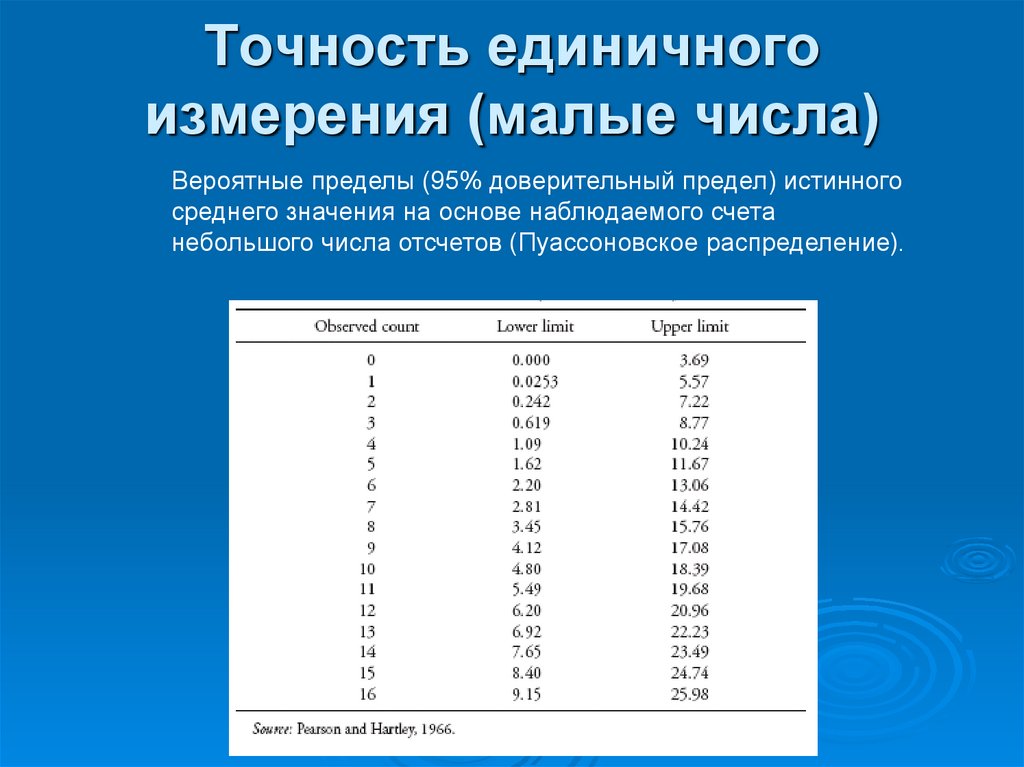
96. Точность единичного измерения (малые числа)

Вероятные пределы (95% доверительный предел) истинного
среднего значения на основе наблюдаемого счета
небольшого числа отсчетов (Пуассоновское распределение).

97. Влияние фона

Если измерение содержит также значительный вклад
фона излучения, фоновое значение необходимо
вычесть.
Значения повторяющихся значений фона также
случайные величины и подчиняются закону
нормального распределения.

98. Влияние фона

Разность между значениями пробы и значениями
фона также подчиняется закону нормального
распределения фона с истинным средним
значением, равном разности между истинным
средним значением пробы и истинным средним
значением фона, но с изменчивостью, большей, чем
отдельно изменчивость отсчетов для пробы и
фоновых отсчетов.
Если периоды счета пробы и фона одинаковые,
лучшей оценкой стандартного отклонения разности
является корень квадратный из суммы двух
измерений, за исключением случаев, когда они
состоят только из небольшого числа отсчетов.

99. Влияние фона

Фоновый счет (600 с) = 380 отсчетов
Счет пробы (600 с) = 650 отсчетов
Чистые отсчеты = 650 – 380 = 270 отсчетов
Ст. откл. разности с = √(650 + 380) = 32,1 отсчетов
95% дов. уровень (1,96 с) = 62,9 отсчетов
Разность можно выразить как 270 ± 63, при 95%
доверительном уровне.
Для получения скорости счета, необходимо
поделить на 600 с: 0.45 ± 0.10 имп/с

100. Влияние фона

Если времена счета пробы и фона разные,
S B
R
t t
s
B
Где S и B – суммарные отсчеты пробы и фона,
накопленные за времена tS и tB, соответственно.

101. Влияние фона

Стандартное отклонение чистой скорости счета
рассчитывается как:
S
B
s 2 2
tS
tB
Где S и B – суммарные отсчеты пробы и фона,
накопленные за времена tS и tB, соответственно.

102. Влияние фона

Фоновый счет(60 с) = 45 отсчетов
Счет пробы (600 с) = 3300 отсчетов
Чистая скорость счета = 4,75 имп/с
Ст.откл. разности с = 0,147 имп/с
95% дов. уровень (1,96 с) = 0,288 имп/с
Результат = 4.75 ± 0,29 имп/с

103. Недостаток радиометрических приборов

Невозможность проводить достоверные
измерения активности без информации о
радионуклидом составе пробы.

104.

Радиометрия является простым и
мощным средством дозиметрического
контроля.

105. Требование к времени измерения при измерении низких уровней активности

Для установок с постоянным фоном
1
I
t
d F A d F A
F
min
2
2
i
2
2
min
F
2
где: t – время измерения источника с;
i
If – измеренная скорость счёта фона имп/с
Ii – измеренная скорость счёта имп/с;
d – относительная средне квадратическая
погрешность измерения
F – эффективность регистрации
A – активность источника
1 I I d
d
t I
F
2
1 1 4 d I t
A 8,33 10
d F t
3