16.09,23.09,30.09

1.

Все не так легко, как кажется
Метрология и
электротехнические
измерения

2.

Метрология
(от греч. "metron"- мера, "logos"- учение)
наука об измерениях,
методах и средствах
обеспечения их единства
и требуемой точности

3.

Постулаты метрологии
Аксиома 1.
Без априорной информации
измерение невозможно
Аксиома 2.
Измерение есть не что иное, как
сравнение
Аксиома 3.
Результат измерения без
округления является случайным

4.

Физические величины;
методы и средства их
измерений

5.

ВЕЛИЧИНА
свойство чего-либо, что может
быть выделено среди других
свойств и оценено тем или
иным способом, в том числе и
количественно

6.

ВЕЛИЧИНЫ
РЕАЛЬНЫЕ
ФИЗИЧЕСКИЕ
ИЗМЕРЯЕМЫЕ
НЕФИЗИЧЕСКИЕ
ОЦЕНИВАЕМЫЕ
ИДЕАЛЬНЫЕ
МАТЕМАТИЧЕСКИЕ

7.

СИСТЕМА ФИЗИЧЕСКИХ
ВЕЛИЧИН
совокупность физических величин,
образованная в соответствии с
принятыми принципами, когда
одни величины принимают за
независимые (основные), а другие
определяют как их функции
(производные)

8.

Основные единицы системы SI
Величина
Наименование
Единица
Обозна
чение
Наименование
Обозначение
Основные
Длина
Масса
Время
Сила электрического тока
L
M
T
I
метр
м/m
килограмм
кг/kg
секунда
с/s
ампер
А/А
Термодинамическая
температура Кельвина
Q
кельвин
К/К
Сила света
J
N
кандела
кд/cd
моль
моль/mol
Количество вещества

9.

РАЗМЕРНОСТЬ
ВЕЛИЧИНЫ
выражение, составленное из произведений
символов основных физических величин в
различных степенях и отражающее связь
данной величины с физическими
величинами, принятыми в данной системе
за основные с коэффициентом
пропорциональности, равным 1

10.

Международный стандарт
ISO/IEC 80000
«величины и единицы измерения»
В системе CИ размерность величины Х:
α
β
γ
δ
ε
λ
μ
dimX=L M T I Θ N J
где L, M, T и т.д. – символы основных величин,
α,β,γ,δ,ε,λ,μ показателями размерности
производной физической величины Х

11.

Энергия определяется по уравнению
Е=mc2
где m- масса,
с – скорость света
Размерность массы m:
dim m=M
Размерность скорости с:
dim с=LT-1
Размерность энергии Е:
dim Е = L2MT-2

12.

1.2 ШКАЛЫ ИЗМЕРЕНИЙ:
ТИПЫ, ПРИНЦИПЫ
ПОСТРОЕНИЯ
Рекомендации
по межгосударственной
стандартизации
«ШКАЛЫ ИЗМЕРЕНИЙ.
Термины и определения»
РМГ 83-2007

13.

ШКАЛА ФИЗИЧЕСКОЙ
ВЕЛИЧИНЫ
это упорядоченная
последовательность значений
физической величины,
принятая на основании
результатов точных
измерений

14.

ШКАЛА НАИМЕНОВАНИЙ
шкала измерений качественного свойства,
характеризующаяся только соотношениями
эквивалентности или отличиями проявлений этого
свойства

15.

ШКАЛА ПОРЯДКА
шкала измерений количественного
свойства, характеризующаяся
соотношениями эквивалентности и
порядка по возрастанию (убыванию)
различных проявлений свойства

16.

12- балльная шкала
Бофорта для силы
морского ветра
шкалы твердости
минералов

17.

ШКАЛА ИНТЕРВАЛОВ
(РАЗНОСТЕЙ)
шкала измерений количественного
свойства (величины),
характеризующаяся соотношениями
эквивалентности, порядка,
суммирования интервалов различных
проявлений свойства

18.

Пример: температурные шкалы Цельсия, Фаренгейта и
Реомюра, летоисчисление по различным календарям

19.

ШКАЛА ОТНОШЕНИЙ
шкала измерений количественного
свойства(величины), характеризующаяся
соотношениями эквивалентности, порядка,
пропорциональности (допускающими в
ряде случаев операцию суммирования)
различных проявлений свойства

20.

Пример: шкалы массы, длины, силы электрического тока…

21.

АБСОЛЮТНАЯ ШКАЛА
шкала измерений безразмерной величины
Отличительные признаки :
наличие естественных (не зависящих от принятой системы единиц)
нуля и арифметической единицы измерений;
допустимость только тождественных преобразований;
допустимость изменения спецификаций, описывающих конкретные
шкалы
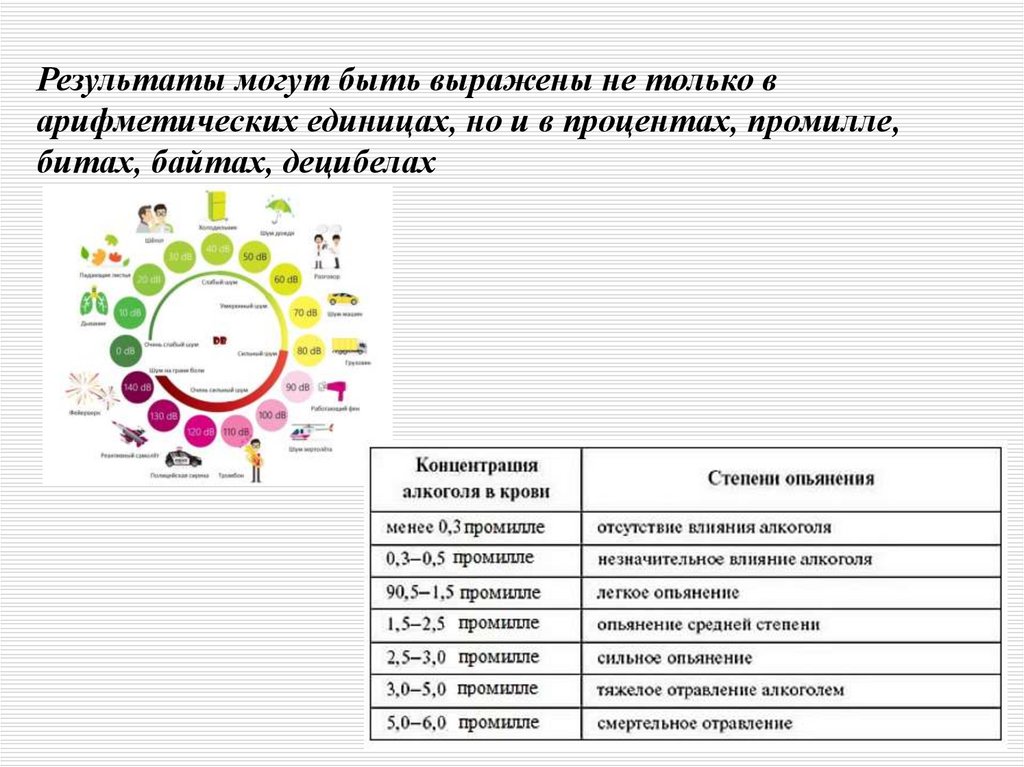
результаты могут быть выражены не только в арифметических
единицах, но и в процентах, промилле, битах, байтах, децибелах

22.

Результаты могут быть выражены не только в
арифметических единицах, но и в процентах, промилле,
битах, байтах, децибелах

23.

1.3 ПРИНЦИПЫ И
МЕТОДЫ ИЗМЕРЕНИЯ
ФИЗИЧЕСКИХ ВЕЛИЧИН
РМГ 29-99 ГСИ. Метрология. Основные термины и определения
МИ 2222-92 ГСИ. Виды измерений. Классификация

24.

Виды измерений
По сложившимся
совокупностям
измеряемых величин
• Электрические
• Механические
• Физико-химические и др.
По зависимости от
места проведения
• Лабораторные
• Промышленные
По зависимости от
формы представления
результатов измерения
• Абсолютные
• Относительные
По числу измерений,
выполняемых для
получения результата
• С однократным наблюдение
• С многократным наблюдением
По характеристике
точности
По способу получения
результата
• Равноточные
• Неравноточные
• Прямые
• Косвенные
• Совокупные
• Совместные

25.

ПРЯМОЕ ИЗМЕРЕНИЕ
Y x
где х - значение величины, найденное
опытным путем

26.

КОСВЕННОЕ ИЗМЕРЕНИЕ
Y f ( x1 , x2 ,..., xn )
где х1, х2,…, хn- результаты прямых измерений
величин, связанных известной функциональной
зависимостью
f
с
искомым
значением
измеряемой величины Y

27.

СОВОКУПНОЕ И СОВМЕСТНОЕ*
ИЗМЕРЕНИЯ
F1 ( X 1 , X 2 ,..., X n , Y1 , Y2 ,..., Ym , k11 , k12 ,..., k1m ) 0
F ( X , X ,..., X , Y , Y ,..., Y , k , k ,..., k ) 0
n
1
2
m
21
22
2m
2 1 2
................................................................................
Fi ( X 1 , X 2 ,..., X n , Y1 , Y2 ,..., Ym , k i1 , k i 2 ,..., k im ) 0
................................................................................
Fn ( X 1 , X 2 ,..., X n , Y1 , Y2 ,..., Ym , k n1 , k n 2 ,..., k nm ) 0
где Х1,Х2,…,Хn – величины, значения которых определяют
путем прямых измерений,
Y1,Y2,…,Ym – искомые
величины (одноименные или
разноименные*),
kij –
известные коэффициенты

28.

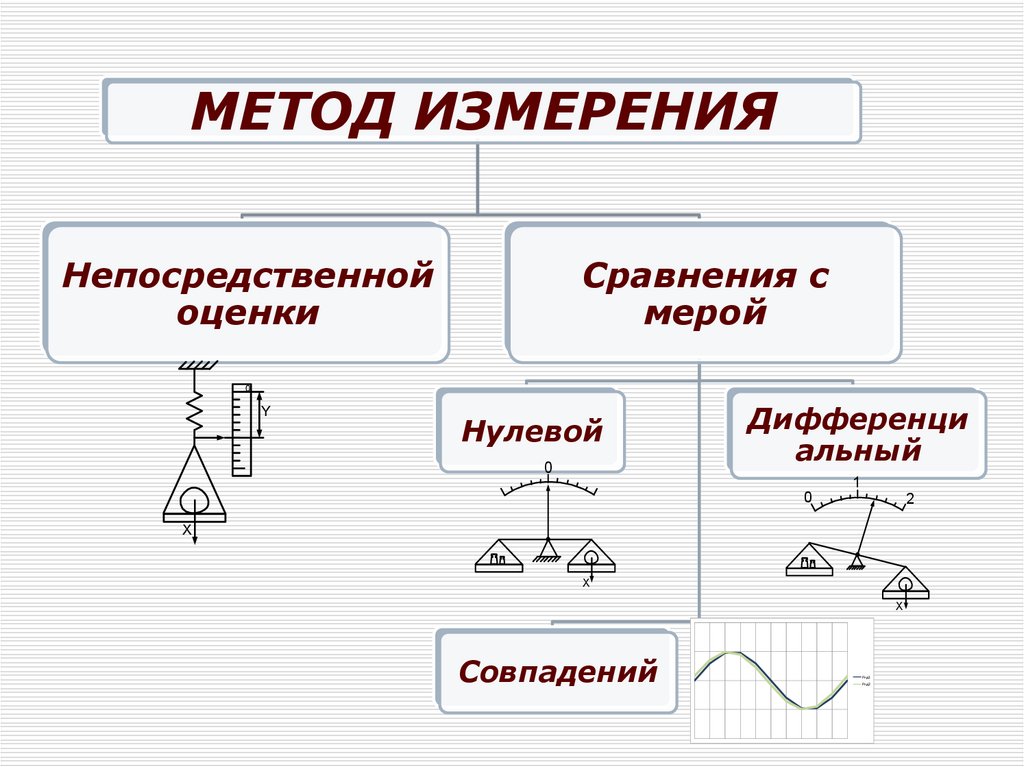
МЕТОД ИЗМЕРЕНИЯ
Непосредственной
оценки
Сравнения с
мерой
0
Y
Нулевой
0
Дифференци
альный
1
0
2
X
X
X
Совпадений
Ряд1
Ряд2

29.

МЕТОД НЕПОСРЕДСТВЕННОЙ
ОЦЕНКИ
0
Y
Y x
X

30.

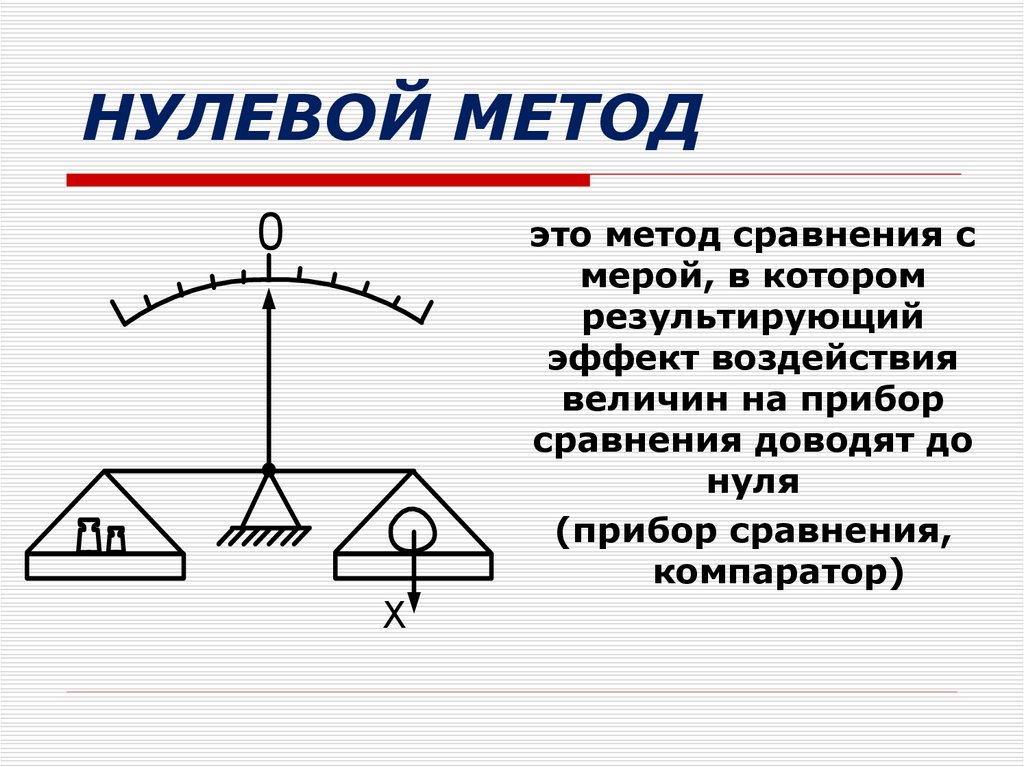
НУЛЕВОЙ МЕТОД
это метод сравнения с
мерой, в котором
результирующий
эффект воздействия
величин на прибор
сравнения доводят до
нуля
(прибор сравнения,
компаратор)
0
X

31.

ДИФФЕРЕНЦИАЛЬНЫЙ
МЕТОД
1
это метод сравнения с
мерой, в котором на
измерительный прибор
воздействует разность
между измеряемой
величиной и известной,
воспроизводимой
мерой
0
2
X

32.

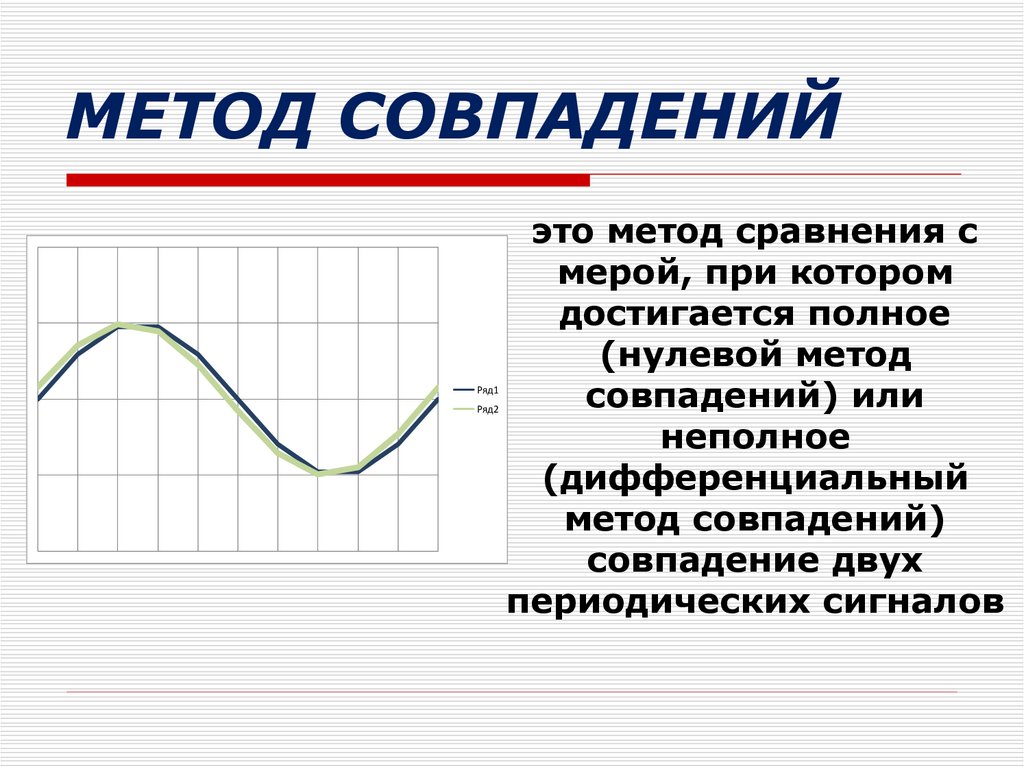
МЕТОД СОВПАДЕНИЙ
Ряд1
Ряд2
это метод сравнения с
мерой, при котором
достигается полное
(нулевой метод
совпадений) или
неполное
(дифференциальный
метод совпадений)
совпадение двух
периодических сигналов

33.

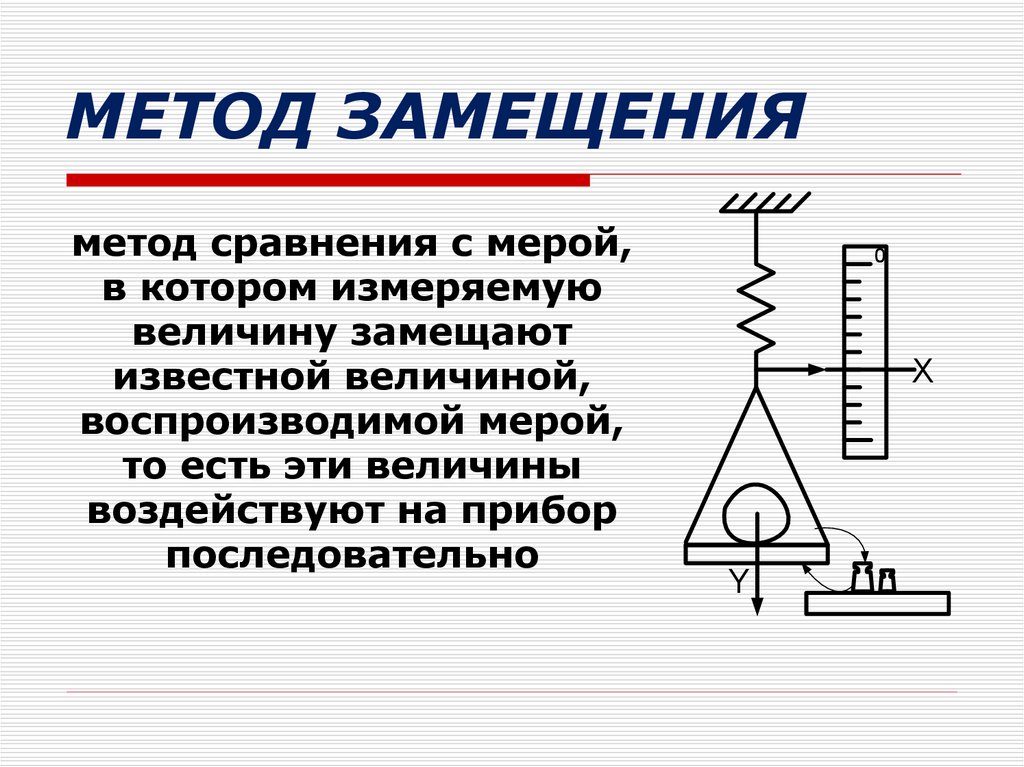
МЕТОД ЗАМЕЩЕНИЯ
метод сравнения с мерой,
в котором измеряемую
величину замещают
известной величиной,
воспроизводимой мерой,
то есть эти величины
воздействуют на прибор
последовательно
0
X
Y

34.

1.4Средства измерений:
классификация,
характеристики

35.

По роли в системе
обеспечения единства
измерений
• метрологические,
• рабочие
По уровню автоматизации
• неавтоматические;
• автоматизированные
• автоматические
По уровню стандартизации
• стандартизованные
• не стандартизованные
По отношению к
измеряемой физической
величине
По функциональному
назначению
• основные
• вспомогательные
• эталоны
• меры
• измерительные приборы
• измерительные преобразователи
• измерительные установки
• измерительные системы

36.

Эталон
средство измерения,
обеспечивающее хранение и
воспроизведение единицы с целью
передачи ее размера
нижестоящим по поверочной
схеме С.И., выполненное по особой
спецификации и официально
утвержденное в установленном
порядке в качестве эталона

37.

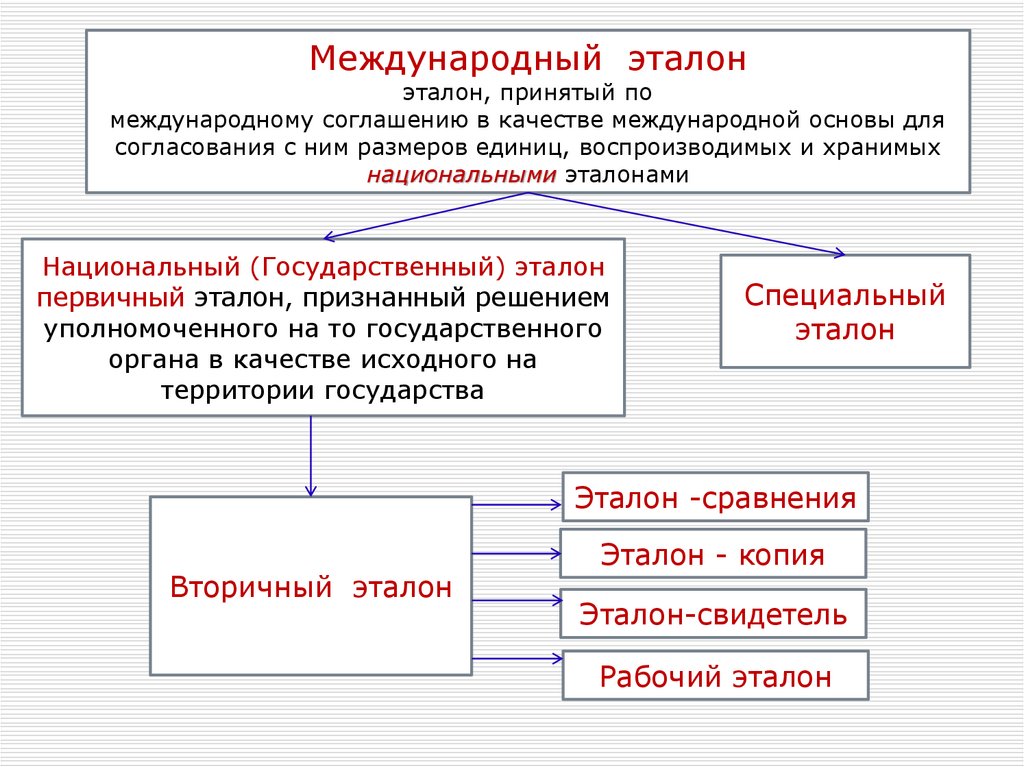
Международный эталон
эталон, принятый по
международному соглашению в качестве международной основы для
согласования с ним размеров единиц, воспроизводимых и хранимых
национальными эталонами
Национальный (Государственный) эталон
первичный эталон, признанный решением
уполномоченного на то государственного
органа в качестве исходного на
территории государства
Специальный
эталон
Эталон -сравнения
Вторичный эталон
Эталон - копия
Эталон-свидетель
Рабочий эталон

38.

ЭТАЛОН ЕДИНИЦЫ ДЛИНЫ –
МЕТРА
В 1872 г. Международная метрическая комиссия
приняла решение об отказе от "естественных"
эталонов длины и о принятии архивного метра в
качестве исходной меры длины.
По нему был изготовлен 31 эталон в виде
штриховой меры длины – бруса из сплава Pt
(90%) и lr (10%).
Поперечное сечение эталона имеет форму Х ,
придающую ему необходимую прочность на
изгиб.
Вблизи концов нейтральной плоскости эталона
нанесено по 3 штриха.

39.

ЭТАЛОН ЕДИНИЦЫ
МАССЫ –
КИЛОГРАММА
Современным эталоном килограмма
является цилиндрическая гиря высотой
и диаметром 39 миллиметров, что
хранится в Международном бюро мер
и весов в Севре (пригород Парижа,
Франция). Эта гиря отлита в 1879 году
из сплава платины (90%) и иридия
(10%)
Прототип был утвержден первый
Генеральной конференцией мер и
весов в 1889 году.

40.

Поверочная схема
утвержденный в определенном
порядке документ,
устанавливающий средства,
методы и точность передачи
размера единиц от эталона или
исходного образцового средства
измерений рабочим средствам
измерений

41.

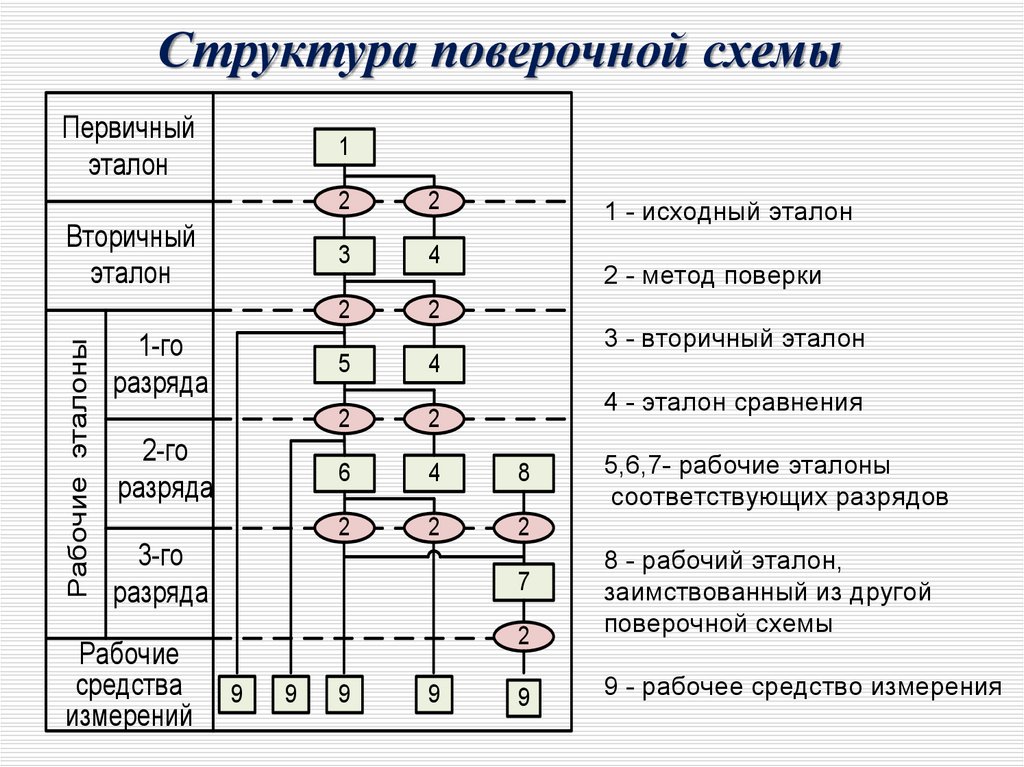
Структура поверочной схемы
Первичный
эталон
1
Рабочие эталоны
Вторичный
эталон
1-го
разряда
2-го
разряда
2
2
3
4
2
2
5
4
2
2
6
4
8
2
2
2
3-го
разряда
Рабочие
средства
измерений
1 - исходный эталон
2 - метод поверки
3 - вторичный эталон
4 - эталон сравнения
2
8 - рабочий эталон,
заимствованный из другой
поверочной схемы
9
9 - рабочее средство измерения
7
9
9
9
9
5,6,7- рабочие эталоны
соответствующих разрядов

42.

Мера
средство измерения,
предназначенное для
воспроизведения физической
величины заданного размера
Выделяют:
однозначные меры;
многозначные меры;
наборы мер

43.

Измерительный прибор
средство измерений,
предназначенное для выработки
сигнала измерительной
информации в форме, доступной
для непосредственного восприятия
наблюдателем

44.

ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
по способу представления
информации
• показывающий
• регистрирующий
по методу измерений
• прямого действия
• сравнения
по форме представления
показаний
• аналоговый
• цифровой
по виду используемой
энергии (физическому
явлению)
• электромеханические,
• электротепловые,
• электрохимические
по роду измеряемой
величины
• вольтметры,
• амперметры,
• частотомеры и т. д.

45.

Измерительный
преобразователь
средство измерения,
предназначенное для выработки
сигнала измерительной
информации в форме, удобной для
передачи, дальнейшего
преобразования, обработки и
хранения, но не поддающейся
непосредственному восприятию
наблюдателем

46.

ИЗМЕРИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
по характеру
преобразования
• аналоговый
• аналого-цифровой
• цифро-аналоговый
по месту в
измерительной
цепи
• первичный
• датчик
• промежуточный
по принципу
действия
• генераторные
• параметрические

47.

Измерительная установка
совокупность функционально
объединенных средств измерений и
вспомогательных устройств,
расположенных в одном месте,
предназначенная для выработки
сигналов измерительной
информации в форме, удобной для
непосредственного восприятия
наблюдателем

48.

Информационноизмерительная система
совокупность средств измерений и
вспомогательных устройств,
соединенных между собой
каналами связи, предназначенная
для выработки сигналов
измерительной информации в
форме удобной для автоматической
обработки, передачи и
использования в АСУ

49.

Режимы работы и
характеристики
средств измерений

50.

Статические
характеристики
Динамические
характеристики
• Градуировочная
характеристика
• Информативный параметр
входного сигнала
• Неинформативный параметр
входного сигнала
• Чувствительность средства
измерения
• Порог чувствительности
средств измерения
• Вариация (гистерезис)
средств измерения
• Разрешающая способность
средств измерения
• Входной (выходной)
импеданс
• Дифференциальное
уравнение:
• Передаточная функция
• Переходная характеристика
• Скорость измерения
(преобразования)
• Время измерения
(преобразования)
• Комплексная частотная
функция,
• Импульсная переходная
характеристика,
• АФХ,
• Время реакции,
• АЧХ,
• ФЧХ,

51.

ХАРАКТЕРИСТИКИ
СТАТИЧЕСКОГО РЕЖИМА
ГРАДУИРОВОЧНАЯ ХАРАКТЕРИСТИКА
Х вых
ЛИНЕЙНАЯ
И
Х вых
Х в ых Х в х
НЕЛИНЕЙНАЯ
Х вых Х вх2
Х в ых А 1 еxp( Xв х / C
Х вх
Х вх

52.

Чувствительность средства
измерения
отношение изменения
выходной величины к
вызывающему его изменению
входной величины
Y
Y Х в х
dy
S
Х вх
dx
tg

53.

Вариация (гистерезис)
средств измерения
разность между показаниями СИ в данной
точке диапазона измерения при возрастании
и убывании измерений величины и
неизменных внешних условиях
H xв x у
xв и x у значения измерений образцовыми СИ
при возрастании и убывании величины x

54.

Входной (выходной)
импеданс
отношение обобщенной силы N к
обусловленной ею обобщенной
скорости W
N
Z
W

55.

Отметка
шкалы
100
Начальное
значение
шкалы
Нижний
предел
измерений
200
указатель
300
400
500
Цена
деления
Диапазон измерений
Диапазон показаний
600
700
Верхний
предел
измерений
Конечное
значение
шкалы

56.

Динамические характеристики
измерительных устройств
Дифференциальное уравнение:
d Y ( )
d Y ( )
dY ( )
an
a n 1
... a1
Y ( ) kX ( )
n
n 1
d
d
d
n 1
n
Передаточная функция:
W ( p)
k
an p n an 1 p n 1 ... a1 p 1
или
Y ( p) W ( p) X ( p)

57.

Динамические характеристики
Переходная
характеристика
временная
характеристика средства измерения, полученная в
результате подачи на его вход сигнала в виде
единичной функции заданной амплитуды:
h(t) X m 1(t)
Она описывает инерционность средства измерения, обусловливающую
запаздывание и искажение выходного сигнала относительно входного

58.

Динамические свойства
также характеризуются
Быстродействием:
Скорость
измерения
(преобразования)
определяется максимальным числом измерений
(преобразований)
в
единицу
времени,
выполняемых с нормированной погрешностью
Время измерения (преобразования) – время,
прошедшее с момента начала измерения
(преобразования) до получения результата с
нормированной погрешностью

59.

1.5 Погрешности
измерений и
средств измерений
ГОСТ Р ИСО 5725-1-2002
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
«ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ
И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ
И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ»

60.

Погрешность измерения
разница между результатами
измерения и истинным
значением измеряемой
величины
Х Х Х ист
Q

61.

Классификация погрешностей
средств измерений
От характера проявления
при повторных
применениях средств
измерений
• Систематическая
• Случайная
От условий применения
средств измерений
• Основная
• Дополнительная
От режима работы
средств измерений
• Статическая
• Динамическая
От формы представления
• Абсолютная
• Относительная
• Приведенная
От характера изменения
измеряемой величины
• Аддитивная
• Мультипликативная
• Гистерезиса
• Линейности

62.

Абсолютная погрешность
разность результата измерения
(показаний прибора Хп) и
действительного Хд значения
измеряемой величины:
X X п X д

63.

Относительная погрешность
отношение абсолютной
погрешности к
действительному значению
измеряемой величины
X
X
100%
Xд

64.

Точность результата
измерения
параметр, характеризующий
близость результата измерения
к истинному (действительному)
значению измеряемой
величины
1
Xд
Х X

65.

Приведенная погрешность
отношение абсолютной
погрешности к нормирующему
значению ХN
X
X
100%
XN

66.

В качестве нормирующего значения используются:
X N X в X н 150 0 150
X N X в X н 250 50 200
X N X в X н 50 50 100
Если указано номинальное значение
измеряемой
величины,
то
за
XN
принимается это номинальное значение

67.

Аддитивная погрешность (или погрешность
нуля) – это погрешность, которая остается
постоянной при всех значениях измеряемой
величины
Y
Y
Y=fp(X)
Y=fp(X)
Y=fн(X)
Xк
Y=fн(X)
X
Систематическая аддитивная погрешность
Xк
X
Случайная аддитивная погрешность

68.

Мультипликативная
погрешность
(или
погрешность
чувствительности)
–
погрешность, которая линейно возрастает (или
убывает) с увеличением измеряемой величины.
Y
Y
Y=fp(X)
Y=fp(X)
Y=fн(X)
Xк
X
Систематическая мультипликативная
погрешность
Y=fн(X)
Xк
X
Случайная мультипликативная
погрешность

69.

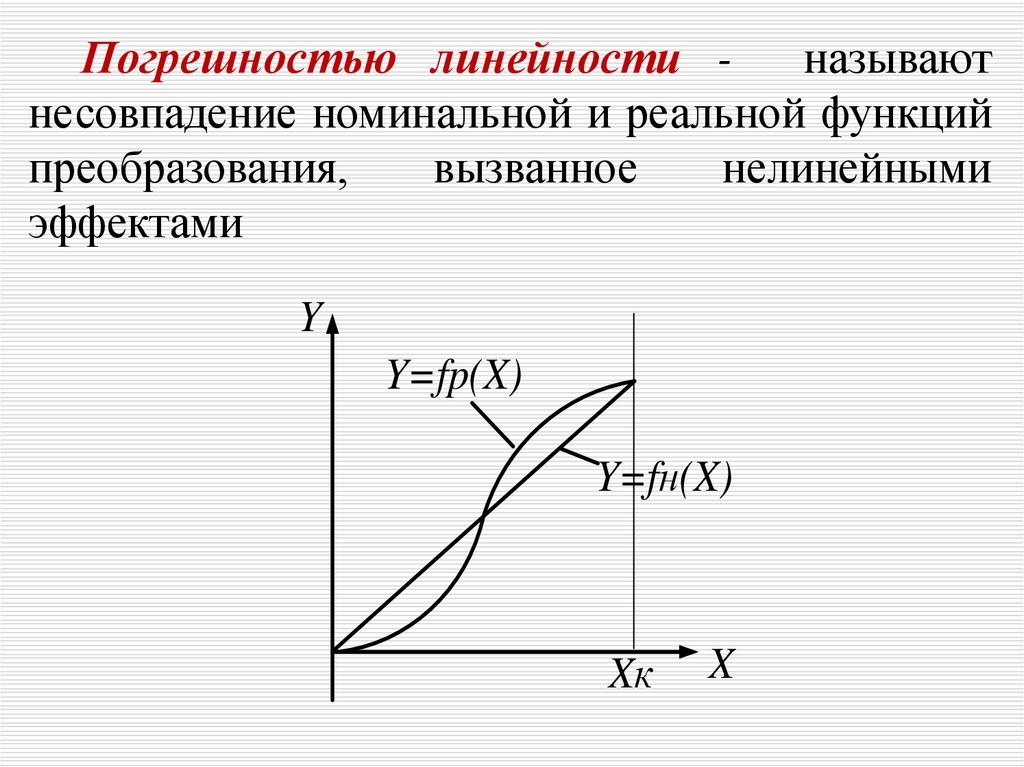
Погрешностью линейности называют
несовпадение номинальной и реальной функций
преобразования,
вызванное
нелинейными
эффектами
Y
Y=fp(X)
Y=fн(X)
Xк
X

70.

Погрешность гистерезиса или погрешность
обратного хода – несовпадение номинальной и
реальной функций преобразования при прямом
и обратном ходе (при постепенном увеличении и
постепенном
уменьшении
измеряемой
величины)
Y
Y=fp(X)
Y=fн(X)
Xк
X

71.

Нормирование
метрологических
характеристик
средств измерений

72.

Нормирование основной
погрешности

73.

1. Если абсолютная погрешность Δ(х) является
мультипликативной,
то
относительная
погрешность при любом х :
( x )
(x)
const
x
и ее используют для нормирования погрешности
и указания класса точности в виде γs.
Граница относительной погрешности результата
измерения
( x) s
Абсолютная погрешность результата измерения:
( x ) s x / 100

74.

2. При аддитивной полосе погрешности для
любых значений х граница абсолютной
погрешности
Δ(x) Δ0 const
Нормируют не абсолютное Δ0, а приведенное
значение этой погрешности:
Δ0
γ0(x)
100
XN
Текущее значение относительной погрешности
обратно пропорционально х
Δ0
δ(x) 100
x

75.

100%
δ
Дn
Дp
γзад
γ0
Δ0
Xk
х
Значение измеряемой величины х=Δ0 при котором
(Δ0)=100% называется порогом чувствительности СИ

76.

100%
Диапазон III
3
Диапазон II
2
Диапазон I
s
0 Хн3
Хн2
Хн1
Хв1
Хв2
(x) 0 / x s x /
Хв3 ¥
0 и ∞ - нижний и верхний пороги чувствительности
Х

77.

3. При смешанном характере полоса абсолютной
погрешностей (x) описывается соотношением и
имеет форму трапеции :
( x) 0 s x

78.

Если уравнение разделить на предел измерения
Xк, то для приведенного значения погрешности
получим:
( x ) 0
x
пр ( x )
s
Xк
Xк
Xк
Обозначив приведенное значение погрешности в
начале диапазона через
0 / X к н
Для приведенного значения погрешности :
x
пр ( x ) н s
Xк

79.

н
s
к
x)/Xк
к н s
х
Xк

80.

Предел допускаемой основной погрешности
нормируется:
к
н
Тогда
относительная
погрешность
результата измерения (в %) определяется по
формуле:
Xк
( x ) к н
1
x

81.

Нормирование
дополнительной
погрешности

82.

Пределы допускаемых дополнительных
погрешностей устанавливают:
в виде постоянного значения для
всей рабочей области влияющей
величины;
путем указания отношения предела
допускаемой дополнительной
погрешности, соответствующего
регламентированному интервалу
влияющей величины, к этому
интервалу;

83.

путем указания функциональной
зависимости пределов допускаемых
отклонений от номинальной функции
влияния.
указанием зависимости предела
допускаемой дополнительной погрешности
от влияющей величины:
дпТ 0.05% / 15 C
0
дпU 0.02% / 10 B
дп 0.01% / 10%

84.

Инструментальная погрешность в рабочих
условиях определяется суммирование пределов
допускаемых
значений
погрешностей
(наименее благоприятный случай сочетания
погрешностей) :
ИП
2
ОП
ИП ОП ДП
2
ДП

85.

КЛАСС ТОЧНОСТИ
Λ
обобщенная характеристика СИ,
определяемая границами
допускаемой основной и
дополнительной погрешностей,
а так же рядом других свойств,
влияющих на точность
измерений

86.

Обозначение классов точности
на средствах измерения
Согласно ГОСТ 8.401-80 (переиздан 2010 г.) для
указания нормированных значений:
погрешности чувствительности γs,
приведенной аддитивной погрешности γ0,
приведенных погрешностей γн и γк
могут использоваться числа из ряда
6; 5; 4; 2,5(3); 2; 1,5(1,6); 1,0 10n ,
где n = 1,0,-1,-2 и т.д., выраженные в %

87.

1.Если класс точности (Λ) установлен по
значению погрешности чувствительности
γs,обозначаемое на шкале значение
класса точности обводится кружком
Например: Λ = 1,5
что означает, что
γs = (x) = 1,5%

88.

2. Если класс точности (Λ) установлен по
значению
приведенной
аддитивной
погрешности γ0, то на шкале обозначается
двумя способами:
1,5 или 1,5
Например:
1,5 - означает, что γ0=γпр=1,5% для всего
диапазона измерений;
1,5 - означает, что γ0=γпр=1,5% для
равномерного участка неравномерной шкалы

89.

3. Обозначение класса точности (Λ) в виде
0,02/0,01 указывает, что погрешность
прибора нормирована по двучленной
формуле с γн=0,01% и γк=0,02%
Xк
( x ) к н 1
x
Xк
( x ) 0,02 0,01 1
x

90.

Выбор средств
измерений

91.

Общие принципы выбора СИ:
1. Для гарантированно заданной или расчетной
относительной погрешности измерения
относительная погрешность СИ должна быть
на 25-30% ниже
си 0,7 и
2. Если известна приведенная погрешность, то
х
СИ и
хN
3. Цена деления шкалы должна выбираться с
учетом заданной точности измерения

92.

Общие принципы выбора СИ:
4. Рабочий участок шкалы СИ должен
выбираться по правилу: относительная
погрешность в пределах него не должна
превышать приведенную погрешность более
чем в 3 раза:
при односторонней равномерной шкале с 0
отметкой в начале рабочий участок
занимает 2/3 длины шкалы;
при двусторонней шкале с 0 отметкой
посередине – последнюю 1/3 каждого
сектора;
При шкале без 0 – рабочий участок может
распространяться на всю длину шкалы

93.

Интегральная функция
распределения случайной
величины X– функция вида:
F ( x ) p( X x )
F ( x ) p( X x)
F(x)
F
1
1
0.5
0.5
M[x]
xi
x
0

94.

Производная от функции распределения
– плотность распределения случайной
величины :
dF ( x )
;
f ( x)
dx
p(x)
x
f ( x)dx F ( x);
1
)
x
(
P
dx
)
x
(
f
M[x]
x

95.

Для оценки результатов измерений
используются центральные
моменты:
1[x] xp( x)dx mx
2 [x] ( x mx ) p( x)dx Dx
2

96.

Нормальный закон
распределения

97.

Плотность вероятности p(X) для закона
нормального распределения случайной
величины Х:
p( X )
1
2
3
Кривая Гаусса 1 2 3
1
2
e
( X M [ X ]) 2
2 2

98.

p( )
- д
д
Доверительным интервалом с границами
от д до д называют интервал, который с
заданной вероятностью Pд , называемой
доверительной, накрывает истинное
значение измеряемой величины

99.

Вероятность P попадания результата
измерения (случайной погрешности) в
заданный интервал [а;в] для нормального
распределения:
а Х
в Х
P(в X а ) Ф
Ф

100.

Равномерный закон
распределения

101.

Симметричное распределение
0, при -a;
1
p( ) , при - a a;
2a
0, при a
2
1
1 x
mx x dx
2a
2a 2
a
a
1/(2а)
p( )
а
-а
0
2
a
Dx x p( x )dx m
3
a
x Dx
3
2
2
x

102.

Вероятность того, что случайная
погрешность результатов измерений ψ
находится в некотором
интервале ( , ) или (- , ) :
P ( ) p( )d
b
a
P ( ) p ( )d
a

103.

Обработка
результатов
измерений

104.

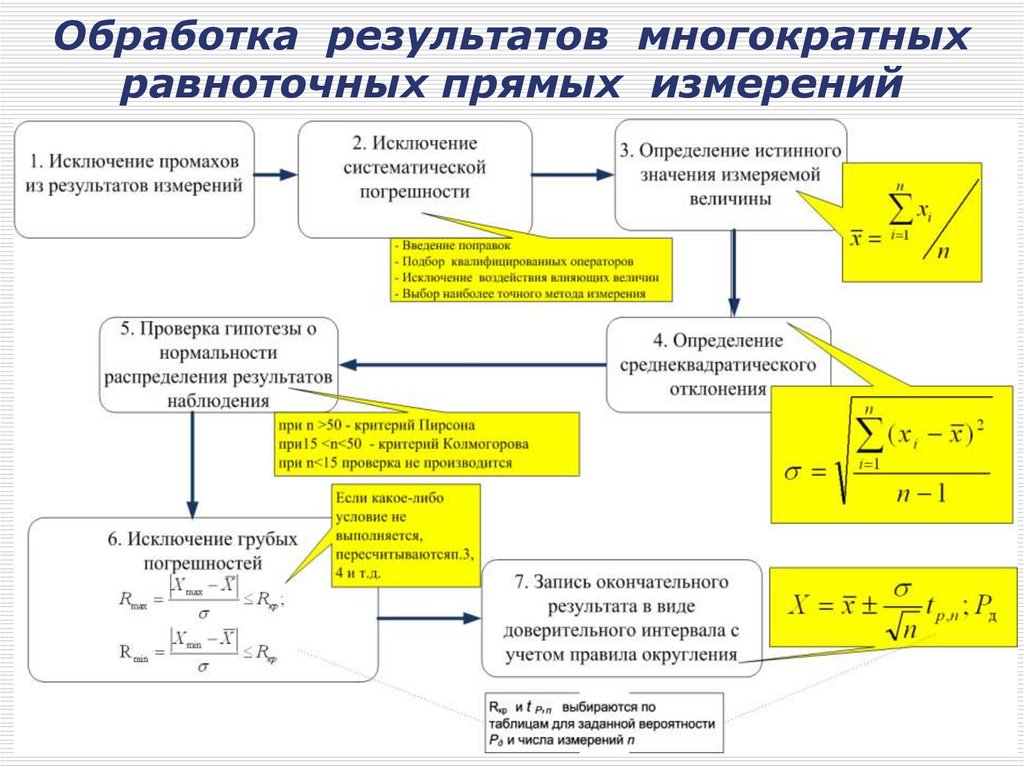
Обработка результатов многократных
равноточных прямых измерений

105.

2. Обработка результатов многократных
неравноточных прямых измерений
Для оценки наиболее вероятного значения
величины по данным неравноточных
измерений вводят «вес» измерения:
gi
ni
2
i
где ni и i - объем и дисперсия i- серии равноточных
измерений
2
Примечание:
g 1
i 1
i

106.

если неравноточные измерения
привели к результатам:
x1 , x2 , , xm
то наиболее вероятным значением
величины будет ее
средневзвешенное значение
m
X ср.взв. m
1
g
i 1
2
i
g i xi
i 1

107.

Обработка результатов
косвенных измерений
Если величина Z является функцией
Z = f (a, b, c,…)
и определяется на основании прямых
измерений величин a, b, c,…

108.

Истинное значение косвенной величины Z
является функцией
Z f (a , b , c ,...)
где a , b , c
измерений
- истинные значения прямых

109.

то среднеквадратическая погрешность измерения
σZ может быть вычислена по формуле:
f f f
z b c ...
a b c
2
2
2
где a, b, c - среднеквадратические погрешности
В случае однократных прямых измерений a, b, c
можно
заменить
абсолютными
соответствующих величин
погрешностями

110.

Задача 1
Случайная величина х подчинена
равномерному закону в интервале от 0 до 2.
Определить математическое ожидание и
дисперсию величины y=6x2

111.

Задача 2
Погрешность измерения напряжения U
распределена по нормальному закону равна
100 мВ, причем систематическая
погрешность ΔUC равна нулю.
Найдите вероятность того, что результат
измерения U отличается от истинного
значения напряжения UИ не более, чем на
240мВ.

112.

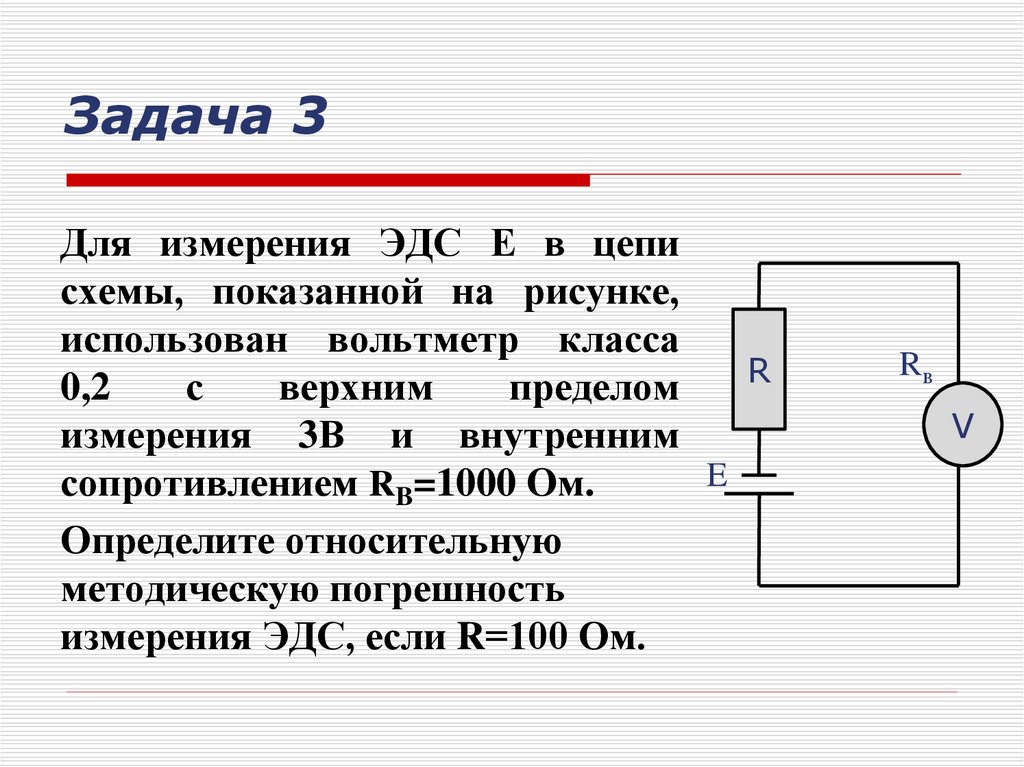
Задача 3
Для измерения ЭДС Е в цепи
схемы, показанной на рисунке,
использован вольтметр класса
R
0,2
с
верхним
пределом
измерения 3В и внутренним
E
сопротивлением RB=1000 Oм.
Определите относительную
методическую погрешность
измерения ЭДС, если R=100 Ом.
Rв
V

113.

Задача 4
В схему, изображенную на рисунке, для
Rа
μА
измерения тока включается
микроамперметр класса точности 1.5,
U
R
имеющий верхний предел измерения
1мкА и внутреннее сопротивление
Ra=7300 Ом.
При U=15 мВ и R=10 кОм определите:
1) относительную методическую погрешность измерения
тока микроамперметром;
2) наибольшую относительную погрешность результата
измерения тока микроамперметром класса 1,5 с
пределом измерения 1 мкА.

114.

Задача 5
В результате равноточных измерений получено
10 значений напряжения:
11В; 10,5В; 11,3В; 10В; 11,1В;
10,2В; 11,4В, 11,8В; 10,2В; 10,6В.
Определить
математическое
ожидание
напряжения и доверительный интервал с
доверительной вероятностью р = 0,95.
Rкр (р=0,95; n=10) = 2,29; tα,n=2,26

115.

Задача 6
Необходимо измерить ток I=4 А имеются два
амперметра: один класса точности 0,5 имеет верхний
предел измерения 20 А, другой класса точности 1,5
имеет верхний предел измерения 5 А.
Определить. у какого прибора меньше предел
допускаемой основной относительной погрешности и
какой прибор лучше использовать для измерения тока
4 А?

116.

Задача 7
На вольтметре класса точности 2,5 с пределом
измерения Uk=300В был получен отсчет
измеряемого
напряжения
U=267,5В.
Определить абсолютную и относительную
погрешность измерения напряжения.

117.

Задача 8
Рассчитать
порог
чувствительности,
погрешность
чувствительности
и
относительную погрешность измерения
напряжения вольтметром, предел шкалы
которого равен 100 В.
Результат измерения Uр = 75,6 В.
Нормированная погрешность вольтметра
обозначена 1,5/0,5.

118.

Задача 9
Погрешность
частотомера
нормирована
путем
указания
интервалов
измерения
частоты
гармонического сигнала, в пределах которых величина
погрешности не превышает заданного значения.
Относительная погрешность не превышает:
0,1% для диапазона частот 10 10 6 Гц
0,5% 5 2 10 6 Гц
2,5% 1 4 10 6 Гц
10,0% 0,25 10 7 Гц
Определить относительную погрешность измерения
частоты 4,5 Гц и 1,7 МГц?

119.

Задача 10
Рассчитать абсолютную и относительную
погрешность измерения сопротивления
методом «вольтметра – амперметра» если
характеристики приборов следующие:
Амперметр
I=4.8 A;
Iк=10 А;
Λ=2,5
Вольтметр
U=80 В;
Uк=100В;
Λ=0,5/0,1

120.

Задача 11
При измерении температуры Т в помещении
термометр
показывает
26˚С.
Среднее
квадратическое отклонение показаний σТ=0,3˚С.
Систематическая погрешность измерения
Δс=+0,5˚С.
Укажите доверительные границы истинного
значения температуры с вероятностью Р=0,9973
(tр=3).

121.

Задача 12
При определении класса точности ваттметра,
рассчитанного на 750 Вт, получили следующие
данные:
46 Вт — при мощности 50 Вт;
103 Вт - при 100 Вт;
196 Вт - при 200 Вт;
403 Вт - при 400 Вт;
746 Вт - при 750 Вт.
Каков класс точности прибора?