lk_2_Mat_osnova

1. Математическая основа карт

Математическая картография:
1.1. Земной эллипсоид
1.2. Масштабы карт
1.3. Картографические проекции
1.4. Географические сетки. Географические координаты
1.5. Разграфка,
рамка карты
номенклатура,
Математическая картография изучает
способы отображения поверхности Земли на плоскости

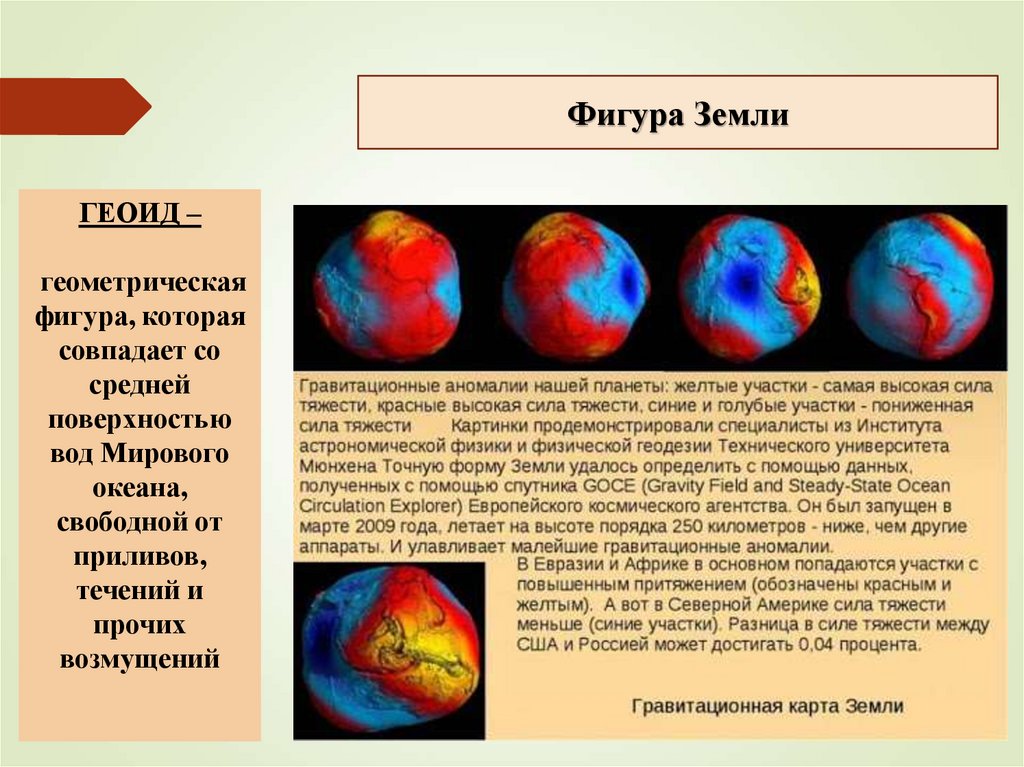
2. ГЕОИД – геометрическая фигура, которая совпадает со средней поверхностью вод Мирового океана, свободной от приливов, течений и

Фигура Земли
ГЕОИД –
геометрическая
фигура, которая
совпадает со
средней
поверхностью
вод Мирового
океана,
свободной от
приливов,
течений и
прочих
возмущений

3.

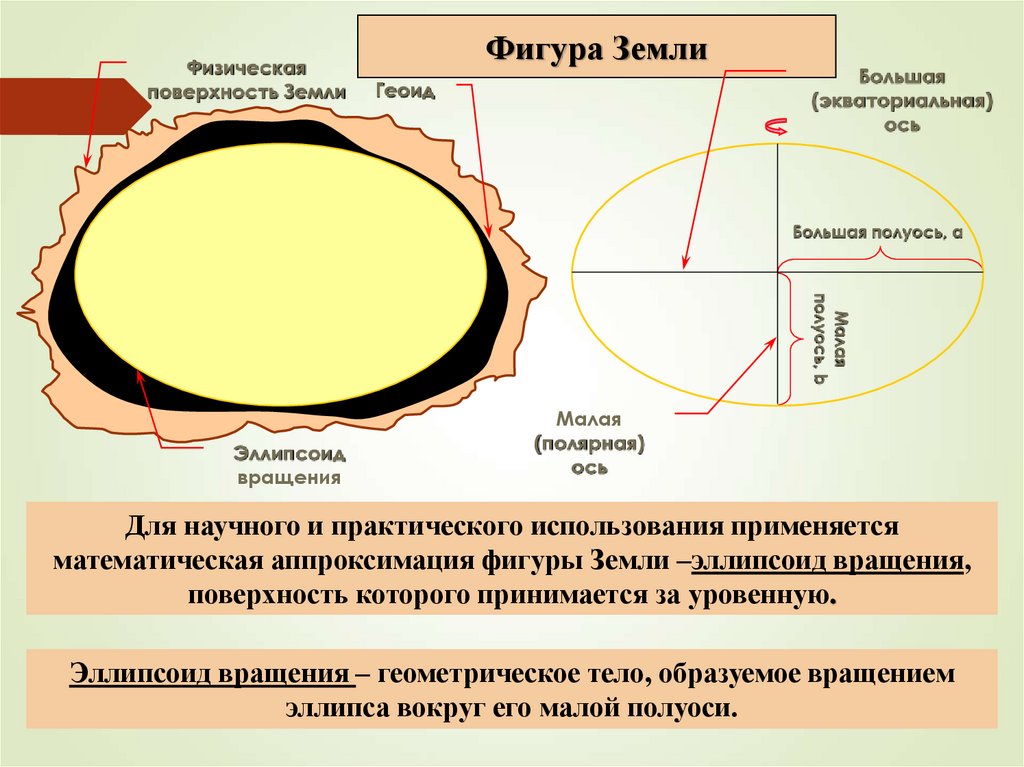
Физическая
поверхность Земли
Фигура Земли
Геоид
Большая
(экваториальная)
ось
Большая полуось, а
Малая
полуось, b
Эллипсоид
вращения
Малая
(полярная)
ось
Для научного и практического использования применяется
математическая аппроксимация фигуры Земли –эллипсоид вращения,
поверхность которого принимается за уровенную.
Эллипсоид вращения – геометрическое тело, образуемое вращением
эллипса вокруг его малой полуоси.

4.

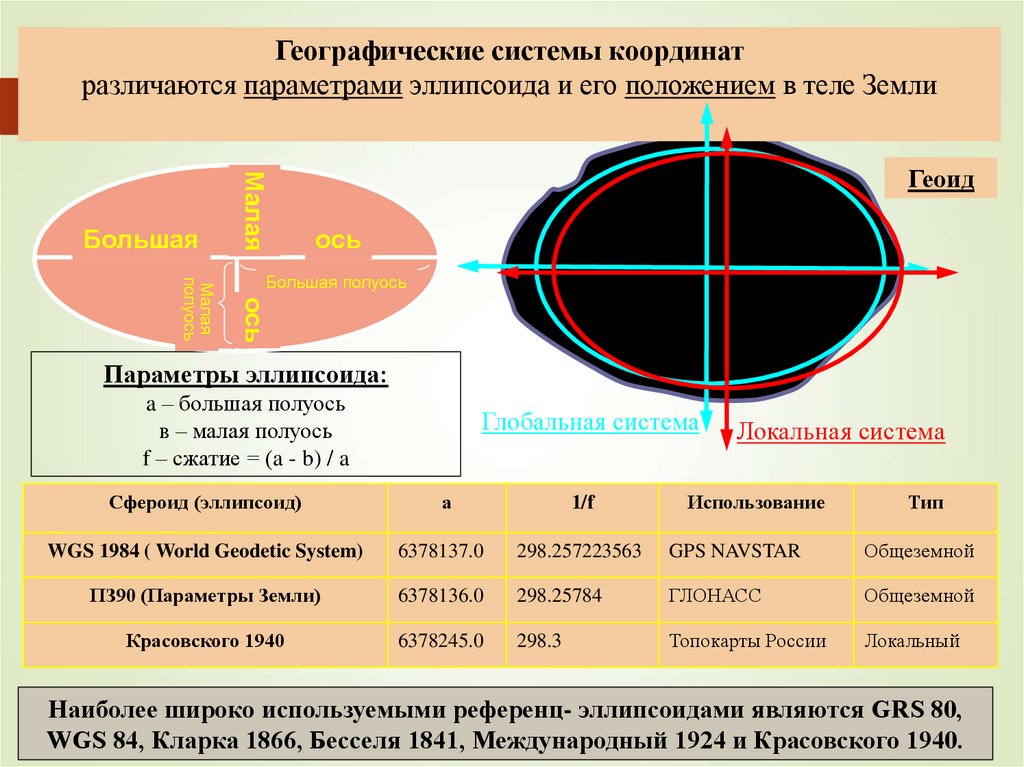
Географические системы координат
различаются параметрами эллипсоида и его положением в теле Земли
Малая
Большая
Геоид
ось
ось
Малая
полуось
Большая полуось
Параметры эллипсоида:
a – большая полуось
в – малая полуось
f – сжатие = (a - b) / a
Глобальная система
Локальная система
Сфероид (эллипсоид)
а
1/f
Использование
Тип
WGS 1984 ( World Geodetic System)
6378137.0
298.257223563
GPS NAVSTAR
Общеземной
ПЗ90 (Параметры Земли)
6378136.0
298.25784
ГЛОНАСС
Общеземной
Красовского 1940
6378245.0
298.3
Топокарты России
Локальный
Наиболее широко используемыми референц- эллипсоидами являются GRS 80,
WGS 84, Кларка 1866, Бесселя 1841, Международный 1924 и Красовского 1940.

5. Феодосий Николаевич Красовский   (1878- 1948) - советский астроном- геодезист, член-корреспондент Академии Наук СССР (1939).

Феодосий
Николаевич Красовский
(1878- 1948) - советский астроном- геодезист,
член-корреспондент
Академии
Наук
СССР (1939). Под его руководством были
определены размеры земного референц эллипсоида (эллипсоид Красовского).
Изотов Александр Александрович
(1907-1988) - геодезист, д.т.н., профессор, проректор
МИИГАиК. Родился в чувашской семье.
Ученик Ф. Н. Красовского, под
его руководством проводил
работы по определению фигуры
Земли. Формулы Изотова А.А.
вошли во все учебники по
геодезии. Работал заместителем
директора по научной работе в
ЦНИИГАиК в лаборатории
космической геодезии.
На эллипсоиде Красовского
основана
геодезическая
система
координат
Пулково-1942
(СК-42),
СК-63,
используемая в России и некоторых других странах,
а также системы координат Afgooye и Hanoi 1972.
С 1 июля 2002 года согласно Постановлению
Правительства Российской Федерации № 568 для
карт России введена новая система СК-95.

6. Современные общеземные эллипсоиды: GRS80 (Geodetic Reference System 1980) разработан Международной Ассоциацией Геодезии и

В России принят референц-эллипсоид Ф.Н. Красовского, вычисленный в 1940 г.
Его параметры:
большая полуось (a) – 6 378 245 м;
малая полуось (b) – 6 356 863 м;
сжатие α = (a–b)/a – 1: 298,3
Современные общеземные эллипсоиды:
GRS80 (Geodetic Reference System 1980) разработан Международной Ассоциацией
Геодезии и Геофизики (International Union of Geodesy and Geophysics) и рекомендован
для геодезических работ;
WGS 84 (World Geodetic System 1984)
применяется в системе спутниковой навигации GPS;
ПЗ-90 (Параметры Земли 1990 года) используется на территории России для
геодезического обеспечения орбитальных полетов. Этот эллипсоид применяется в
системе спутниковой навигации ГЛОНАСС;
IERS 96 (International Earth Rotation Service 1996) рекомендован Международной
службой вращения Земли для обработки РСДБ-наблюдений.
См. учебник Бугаевского Л.М. Математическая картография:
Учебник для вузов. – М.: 1998. – 400 с. (переизданные)...

7.

Масштабы карт
М 1:5 000 пятитысячная
М 1: 1 000 000 миллионная
Масшта́б (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») —
соотношение, которое показывает, во сколько раз каждая линия, нанесённая на карту
или чертёж, меньше или больше её действительных размеров.
Есть три вида масштаба: численный, именованный, линейный:
выделяют еще масштаб по осям координат, поперечный масштаб;
иррациональный масштаб; десятичный или кратный масштаб.
Точность масштаба — отрезок горизонтального проложения линии,
соответствующий 0,1 мм на плане.
Значение 0,1 мм для определения точности масштаба принято из-за того, что это
минимальный отрезок, который человек может различить невооружённым глазом.
Например, для масштаба 1:10 000 точность масштаба будет равна 1 м.
В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности,
1 мм — 1000 см (10 м),
0,1 мм — 100 см (1 м).

8. Главный масштаб длин представляет степень уменьшения поверхности земного эллипсоида перед последующим изображением его на

плоскости и сохраняется в
зависимости от применяемой картографической проекции в некоторых точках или
линиях, называемых точками и линиями нулевых искажений.
Частным масштабом длин называется отношение бесконечно малого отрезка ds в
данной точке и по данному направлению к соответствующему бесконечно малому
отрезку dS на эллипсоиде, т. е. М = ds/dS.
Частный масштаб длин может быть больше или меньше главного.
Из всех частных масштабов, рассматриваемых в картографии, наибольшее значение
имеют масштабы по меридиану m и параллели n.
Вид карты
Крупномасштабная
Масштаб
Примеры
1:0 — 1:600 000
1:0,00001 — строение вируса
1:100 — план помещения
1:5000 — карта района или
посёлка
Среднемасштабная 1:600 000 - 1:2 000 000
Карта региона, небольшой
страны
Мелкомасштабная
1:100 000 000 — карта мира
1:10²¹ — карта галактики
1:2 000 000 -1:∞

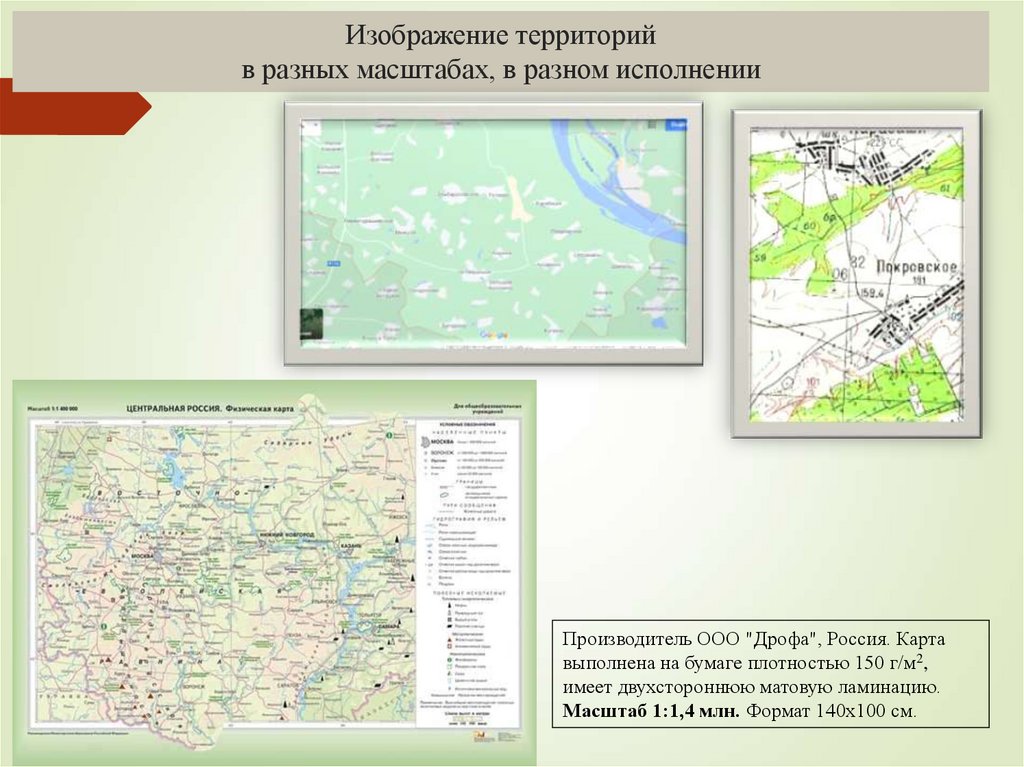
9. Изображение территорий в разных масштабах, в разном исполнении

Производитель ООО "Дрофа", Россия. Карта
выполнена на бумаге плотностью 150 г/м2,
имеет двухстороннюю матовую ламинацию.
Масштаб 1:1,4 млн. Формат 140х100 см.

10. КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ

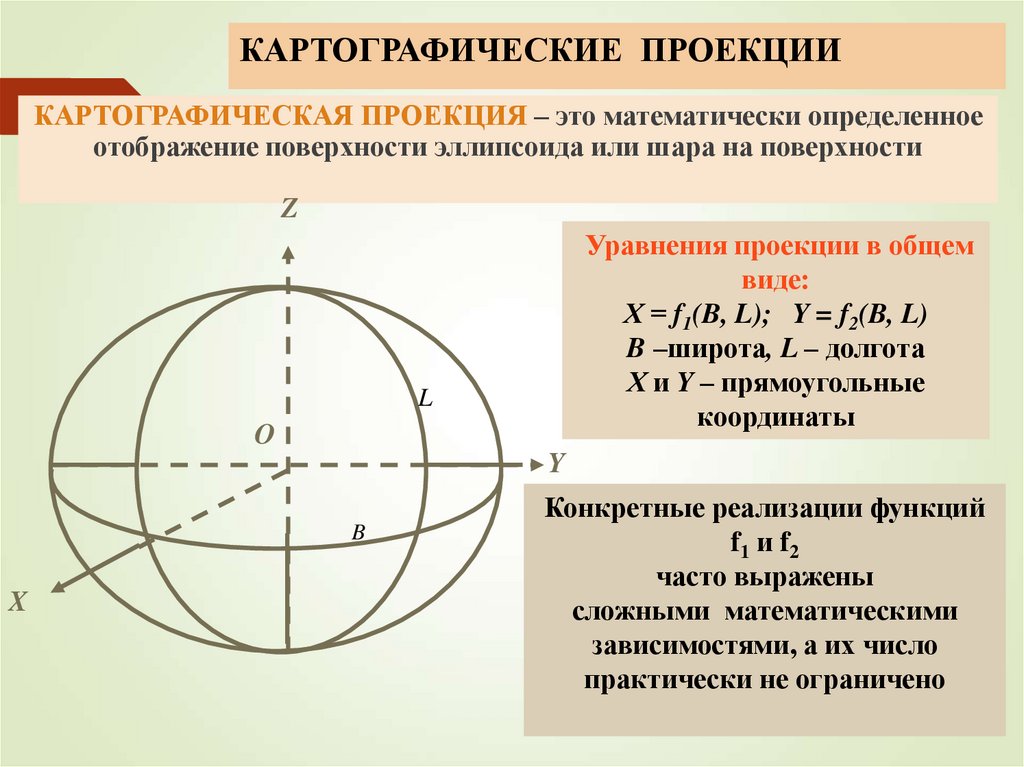
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ – это математически определенное
отображение поверхности эллипсоида или шара на поверхности
Z
Уравнения проекции в общем
виде:
Х = f1(B, L); Y = f2(B, L)
B –широта, L – долгота
Х и Y – прямоугольные
координаты
L
O
Y
B
X
Конкретные реализации функций
f1 и f 2
часто выражены
сложными математическими
зависимостями, а их число
практически не ограничено

11. Пример картографической проекции — проекция Меркатора

Пример картографической проекции — проекция Меркатора
Исходная аксиома!
При изыскании любых
картографических проекций
сферическую
поверхность
земного шара (эллипсоида,
глобуса) нельзя развернуть
на плоскость карты без
искажений
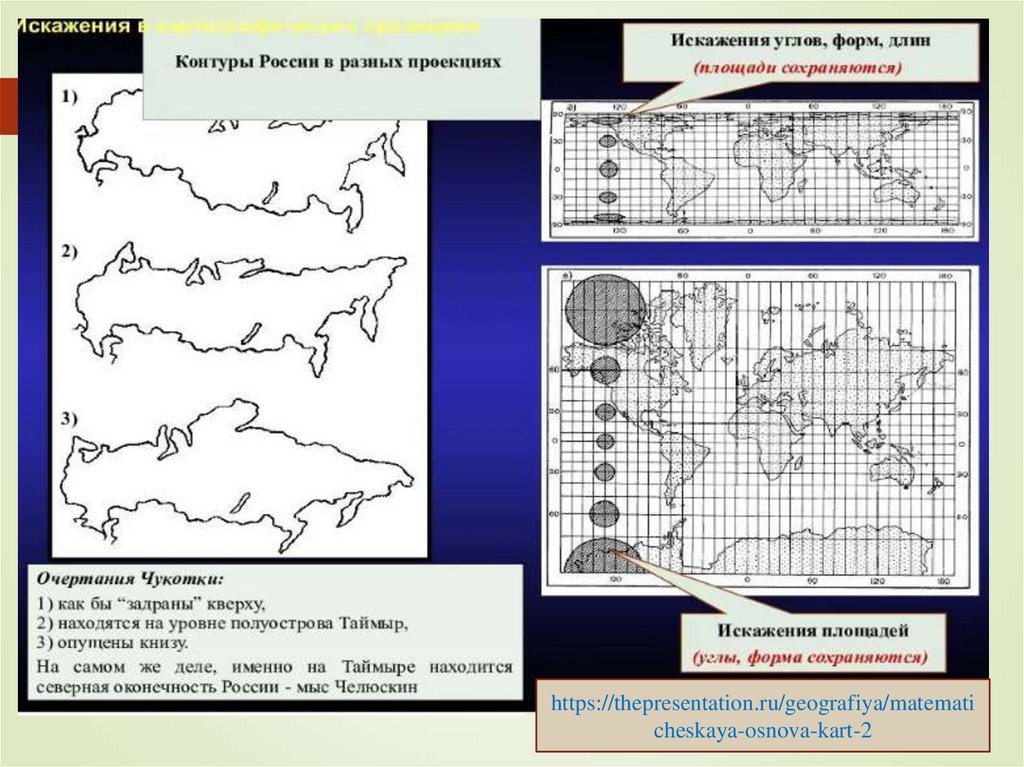
Следующие виды
искажений:
Искажения длин
Искажения площадей
Искажения углов
Искажения форм
Рисунок. Эллипс искажений
В ряде проекций существуют линии и точки, где
искажения отсутствуют. Сохраняется главный
масштаб карты- это линии нулевых искажений.
На картах могут быть проведены изоколылинии равных искажений длин, углов, площадей,
форм.

12.

https://thepresentation.ru/geografiya/matematicheskaya-osnova-kart-2

13.

https://thepresentation.ru/geografiya/matemati
cheskaya-osnova-kart-2

14. Классификация проекций по характеру искажений

Равновеликая проекция —
один из основных типов картографических проекций
Равновел. коническая
проекция Альберса (1805)
Равновеликая цилиндрическая проекция Ламберта
для земного шара, центральный меридиан 160 з.д.
Равновел.
псевдоцилиндрическая
проекция VI Экерта с
синусоидальными
меридианами
Равновел. цилиндрическая
проекция Галла
Равновел. азимутальная
проекция Ламберта

15. Классификация проекций по характеру искажений

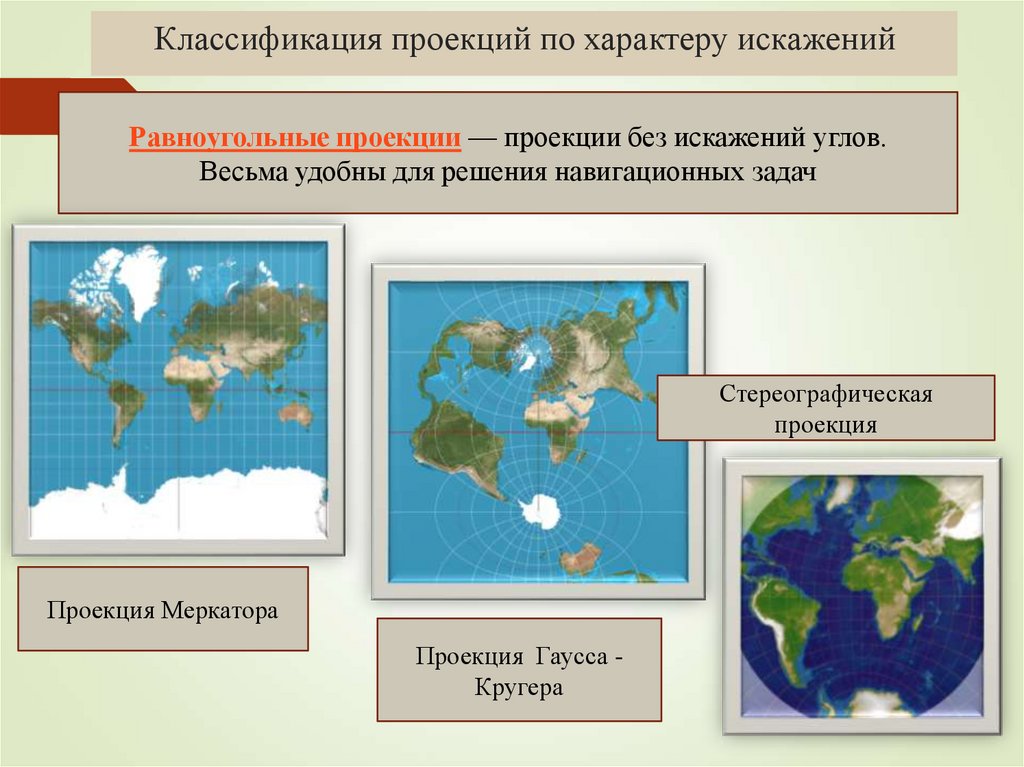
Равноугольные проекции — проекции без искажений углов.
Весьма удобны для решения навигационных задач
Стереографическая
проекция
Проекция Меркатора
Проекция Гаусса Кругера

16. Классификация проекций по характеру искажений

Равнопромежуточная проекция — картографическая проекция,
обладающая свойством сохранения масштаба вдоль определенных линий.
Равнопромежуточные по меридианам
по параллелям
Произвольные проекции

17. Классификация проекций по виду нормальной картографической сетки

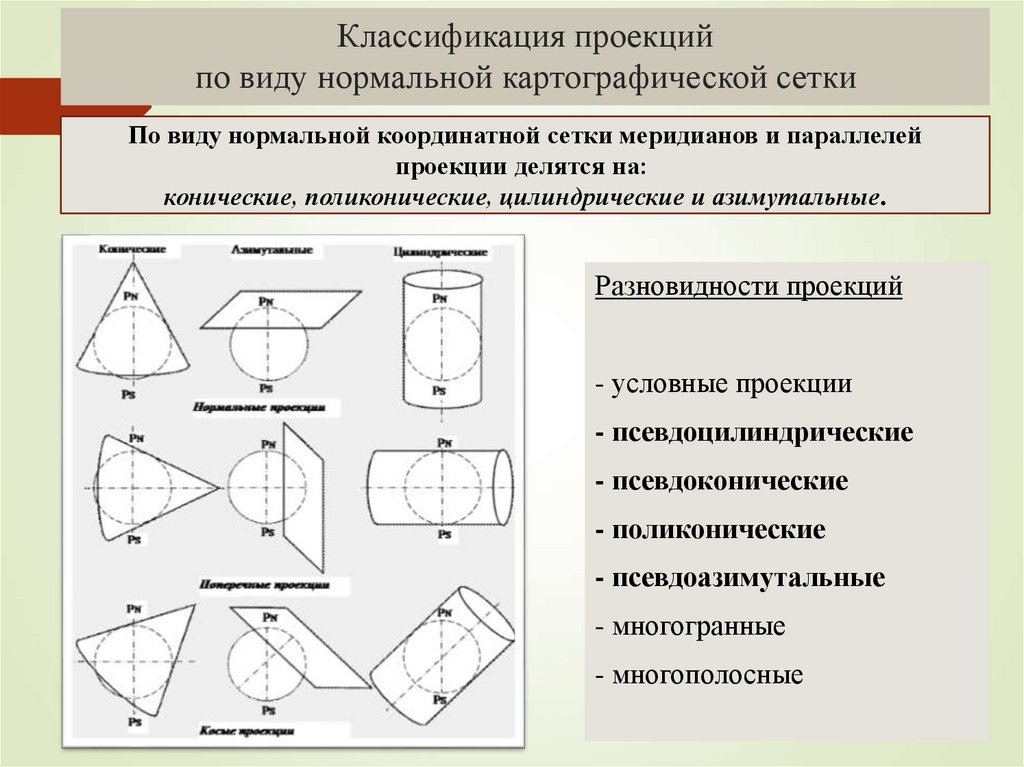
По виду нормальной координатной сетки меридианов и параллелей
проекции делятся на:
конические, поликонические, цилиндрические и азимутальные.
Разновидности проекций
- условные проекции
- псевдоцилиндрические
- псевдоконические
- поликонические
- псевдоазимутальные
- многогранные
- многополосные

18. Проекция Каврайского — картографическая проекция, разработанная В. В. Каврайским в 1939 году  в качестве псевдоцилиндрической

Проекция Каврайского — картографическая проекция,
разработанная В. В. Каврайским в 1939 году в качестве псевдоцилиндрической
проекции общего назначения. Как и проекция Робинсона (англ.), это компромиссная
проекция, направленная на достижение минимальных искажений по всей
поверхности геоида. В этом отношении она превосходит другие популярные
проекции, такие как тройная проекция Винкеля (англ.). Несмотря на прямые
равноотстоящие параллели и простые формулы. Использовалась в Советском Союзе
и практически неизвестна на Западе.

19.

Рис.
.
Картографические
проекции распознаются
по следующим трём
основным типам
признаков:
1) вид (форма) на карте
меридианов и параллелей;
2) соотношение длин дуг
меридианов между
параллелями или
параллелей между
меридианами в двух разных
частях карты или изменение
величины этих дуг в
пределах карты;
3) линия, изображающая
экватор.