Similar presentations:
Классические модели теории вероятностей: монета и игральная кость
1.
КЛАССИЧЕСКИЕ МОДЕЛИТЕОРИИ ВЕРОЯТНОСТЕЙ:
МОНЕТА И ИГРАЛЬНАЯ КОСТЬ
2.
8 классВВЕДЕНИЕ
Многие
важные
и
нужные
факты
первоначально были получены с помощью
очень простых опытов. Большую роль в
развитии теории вероятностей как науки
сыграли обычные монеты и игральные кубики.
ЦЕЛЬ УРОКА:
• Повторить понятия “эксперимент”, “событие” “исход”,
“благоприятный исход”, типы событий и их вероятности.
• изучить роль классических вероятностных моделей
(монета, игральная кость) в теории вероятностей.
• Рассмотреть задачи, связанные с бросанием монеты и
игральной кости.
3.
МОНЕТАМонета с точки зрения теории вероятностей имеет только две
стороны, одна из которых называется “орел”, а другая - “решка”.
Монету бросают, и она падает одной из сторон вверх. Никакие другие
свойства математической монете не присущи.
МАТЕМАТИЧЕСКАЯ
МОНЕТА
СЧИТАЕТСЯ
СИММЕТРИЧНОЙ. ПРИ ЭТОМ ПОДРАЗУМЕВАЕТСЯ, ЧТО
НИКАКОЙ ДРУГОЙ ИСХОД БРОСАНИЯ МОНЕТЫ
НЕВОЗМОЖЕН, - ОНА НЕ МОЖЕТ ПОТЕРЯТЬСЯ,
ЗАКАТИВШИСЬ В УГОЛ, И, ТЕМ БОЛЕЕ, НЕ МОЖЕТ
“ВСТАТЬ НА РЕБРО”.
4.
МОНЕТАНазвание “орел” для обратной стороны (реверса) для монеты происходит от
того, что на реверсе российских монет изображен герб российского
государства - двуглавый орел. Впервые орел появился при великом князе
Иване iii.
В название “решка” для лицевой стороны (аверса) монеты возникло потому, что
рисунок на аверсе российских монет в xviii-xix вв. напоминал решетку, на фоне
которой был написан номинал монеты (ее достоинство).
5.
МОНЕТАМонета часто помогала людям в сложной
положившись на судьбу.
ситуации сделать выбор,
“Великий японский воитель Нобунага решил однажды атаковать врага, который десятикратно
превосходил числом его солдат. Он знал, что победит, но солдаты его уверены не были. В
дороге он остановился у синтоистского храма и сказал:
- Когда я выйду из храма, то брошу монету. Выпадет герб — мы победим, выпадет цифра —
проиграем сражение.
Нобунага вошел в храм и стал безмолвно молиться. Затем, выйдя из храма, бросил монету.
Выпал герб. Солдаты так неистово ринулись в бой, что легко одолели врага.
— Ничего не изменить, когда действует рука судьбы, — сказал ему адъютант после
сражения.
— Верно, не изменить, — подтвердил Нобунага, показывая ему поддельную монету с
гербами на обеих сторонах.”
6.
ИГРАЛЬНАЯ КОСТЬИгральный кубик или игральная кость также служит прекрасным
средством для получения случайных событий. Игральная кость имеет
удивительную историю. Игра в кости - одна из древнейших. Она была
известна в глубокой древности в Индии, китае, египте, Греции и риме.
Игральные кости в виде кубиков находили в египте (xx в. До н.э.) и китае
(vi в. До н.э.) при раскопках древних захоронений. Точки на гранях
древнеегипетских костей часто изображали в вИде птичьего глаза.
7.
ПОВТОРЕНИЕ• Какие события называются случайными?
• Чему равна вероятность достоверного события?
Невозможного события?
• Как вычислить вероятность случайного события?
вероятность события - отношение числа благоприятных этому
событию исходов к общему числу всех равновозможных
несовместных элементарных исходов, образующих полную
группу.
m
____
Р (А) = n
Вероятность всегда больше 0,
но меньше 1!
8.
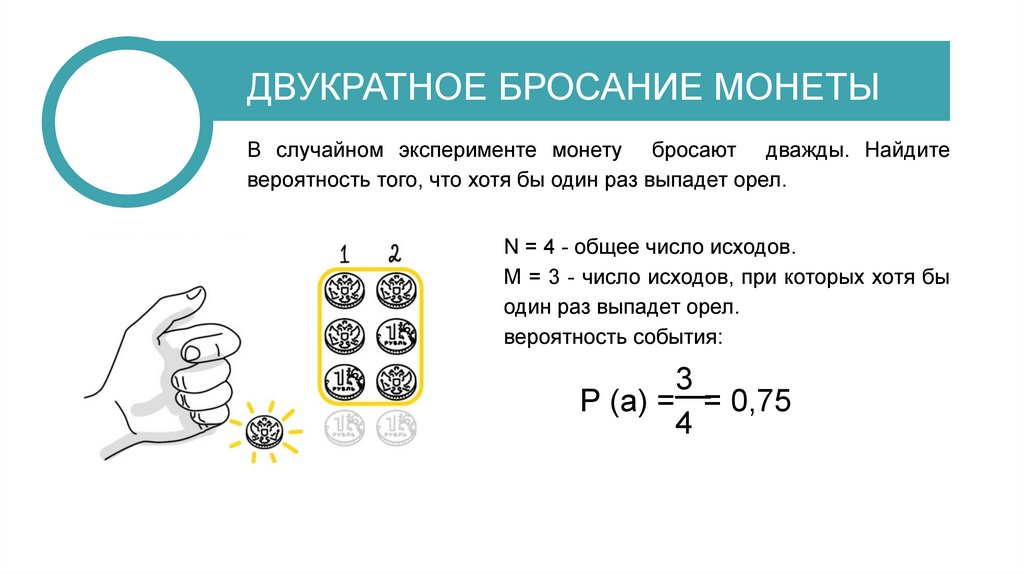
ДВУКРАТНОЕ БРОСАНИЕ МОНЕТЫВ случайном эксперименте монету бросают дважды. Найдите
вероятность того, что хотя бы один раз выпадет орел.
N = 4 - общее число исходов.
M = 3 - число исходов, при которых хотя бы
один раз выпадет орел.
вероятность события:
3
__
Р (а) = = 0,75
4
9.
ЗАКРЕПЛЕНИЕ МАТЕРИАЛА• выпишите
все
элементарные
события
случайного опыта, в котором симметричную
монету бросают 3 раза.
• симметричную монету бросили 2 раза.
Найдите вероятность того, что при первом
броске выпала решка.
• симметричную монету бросили три раза.
Найдите вероятность того, что орел выпал не
менее двух раз.
10.
ДВЕ ИГРАЛЬНЫЕ КОСТИВ случайном эксперименте бросают две игральные кости. Найдите
вероятность того, что в сумме выпадет 3 очка. Результат округлите до
сотых.
Подсказка
На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому
варианту выпадения очков соответствует 6 вариантов выпадения
очков на втором кубике.
варианты исходов будут такие:
1:1 1;2 1;3 1;4 1;5 1;6
2;1 2;2 2;3 2;4 2;5 2;6
…
6;1 6;2 6;3 6;4 6;5 6;6
т.е. всего вариантов 6 • 6 = 36
11.
ЗАКРЕПЛЕНИЕ МАТЕРИАЛА• Игральную кость бросают дважды. Найдите
вероятность того, что сумма двух выпавших
чисел равна 4 или 7.
• Игральную кость бросают дважды. Найдите
вероятность того, что оба раза выпало число,
меньшее 4.
• Игральную кость бросают дважды. Найдите
вероятность того, что сумма двух выпавших
чисел равна 5 или 8.










 mathematics
mathematics








