Similar presentations:
Начертательная геометрия. Ортогональное проецирование
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Лекция 1. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ2. ЦЕЛЬ КУРСА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Развитие пространственного представления ивоображения, необходимых в техническом творчестве
Для создания представления о пространственном объекте
по его проекциям необходима некоторая работа
воображения, тем большая, чем сложнее форма предмета
Научиться не только строить изображения предметов,
но и мысленно воспроизводить в пространстве сами
предметы по их изображениям
2
3. ЛИТЕРАТУРА
1.2.
3.
4.
5.
6.
7.
3
Фролов С.А. Начертательная геометрия. М.:
Машиностроение,1983
Гордон В.О. Курс начертательной геометрии. М.:
Высшая школа, 2004
Крылов Н.Н. и др. Начертательная геометрия. М.:
Высшая школа, 2000
Нартова Л.Г. Начертательная геометрия. М.: Дрофа,
2003
Чекмарев А.А. Начертательная геометрия и черчение.
М.: Высшая школа, 2003
Фролов С.А. Сборник задач по начертательной
геометрии. М.: Машиностроение,1986
Гордон В.О. Сборник задач по курсу начертательной
геометрии. М.: Высшая школа, 2003
4. ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Метрические – задачи на определение длин линий,размеров углов, площадей, объемов
Позиционные – задачи на установление взаимного
положения и взаимопринадлежности
рассматриваемых геометрических объектов
4
5. ГЕОМЕТРИЧЕСКИЕ ОБЪЕКТЫ
ТочкаПрямая
Плоскость
Поверхность
5
6. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
1.2.
3.
4.
6
Точки в пространстве – прописными буквами
латинского алфавита А, В, С, …, а также цифрами
Линии в пространстве – по точкам, определяющим
линию, и строчными буквами латинского алфавита
а, b, c …
Углы – строчными буквами греческого алфавита φ,ψ,ω,σ
Плоскости - α,β,γ,δ
7. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
5.7
Плоскости проекций – строчной буквой греческого
алфавита π
Горизонтальная плоскость π1
Фронтальная плоскость π2
Профильная плоскость π3
Любая дополнительная плоскость π4, π5, … πn
8. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
6.Оси проекций – строчными буквами x, y, z
При введении дополнительных плоскостей -
π₁/ π₄, π₂/ π₄, π₄/ π₅, …
7.
Проекции точек:
8
На плоскость α – Аα
На горизонтальную плоскость π₁ – А₁
На фронтальную плоскость π₂ – А₂
На профильную плоскость π₃ – А₃
На дополнительную плоскость π₄ – А₄
9. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
8.Проекции линий –
по проекциям точек, определяющих линию: A1B1’
A2B2’ A3B3
строчными буквами:
На горизонтальную плоскость π₁ – m₁, n₁…
На фронтальную плоскость π₂ – m₂, n₂, …
На профильную плоскость π₃ – m₃, n₃, …
9
10. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Проецирование предмета из данного центраназывают центральным или коническим
проецированием. Чтобы спроецировать точку В на
плоскость α из данного центра А, надо провести
прямую линию (проецирующий луч) из точки А через
точку В до пересечения с плоскостью проекций α
10
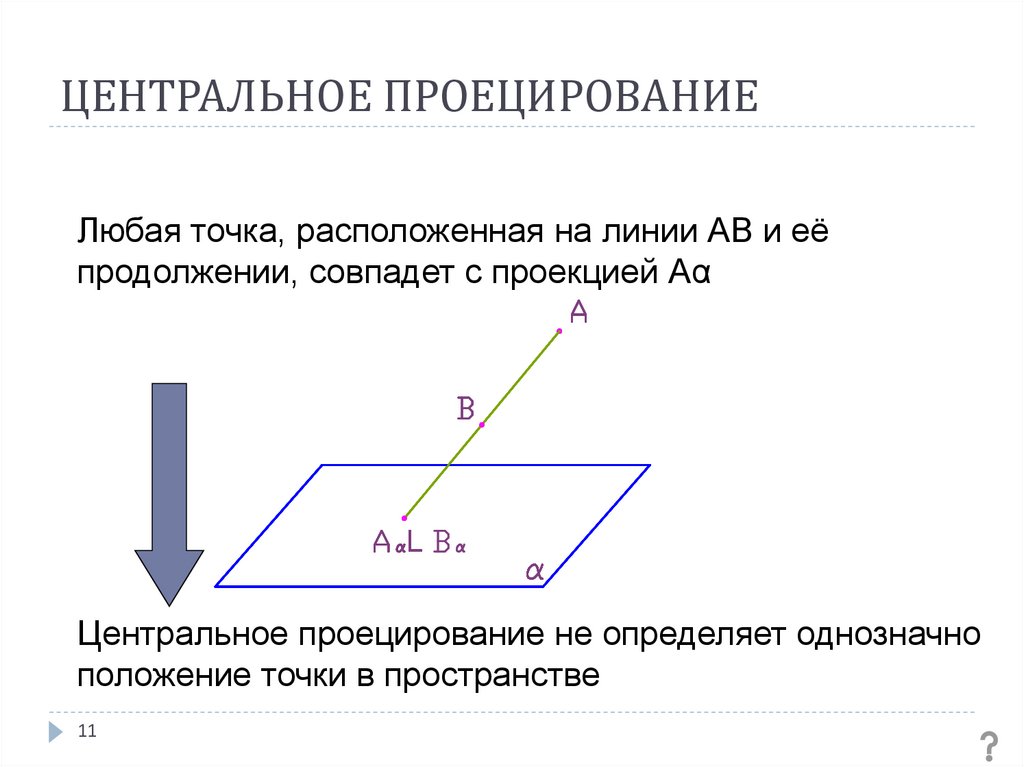
11. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Любая точка, расположенная на линии АВ и еёпродолжении, совпадет с проекцией Аα
L
Центральное проецирование не определяет однозначно
положение точки в пространстве
11
12. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Проецирование предмета из бесконечноудаленного центра называют параллельным или
цилиндрическим. Чтобы спроецировать точку А на
плоскость α, надо провести через эту точку
параллельно направлению проецирования S
прямую линию (проецирующий луч) до пересечения
с плоскостью проекций α
12
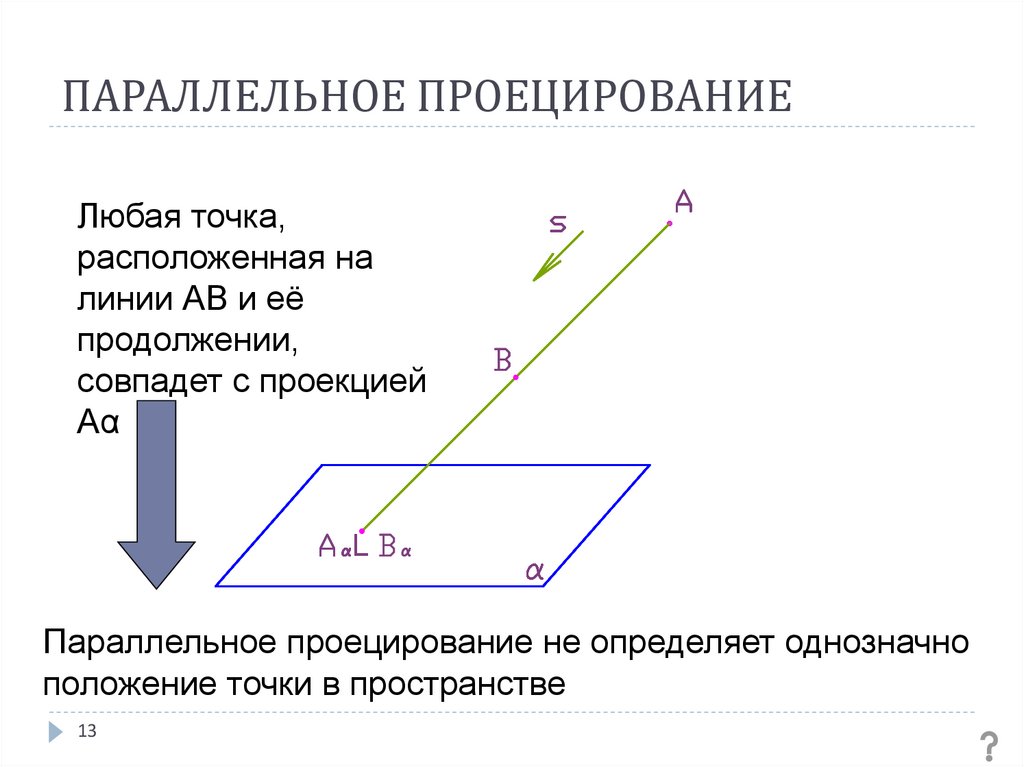
13. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Любая точка,расположенная на
линии АВ и её
продолжении,
совпадет с проекцией
Аα
L
Параллельное проецирование не определяет однозначно
положение точки в пространстве
13
14. ЦЕНТРАЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ. ВЫВОДЫ
Одна центральная проекция как и однапараллельная проекция недостаточна для
однозначного представления предмета: по такому
изображению нельзя определить форму и размеры
предмета и его положение в пространстве
14
15. ОРТОГОНАЛЬНОЕ (ПРЯМОУГОЛЬНОЕ) ПРОЕЦИРОВАНИЕ
Ортогональное проецирование – единственный способпостроения машиностроительных чертежей
Ортогональное проецирование – прямоугольное,
параллельное проецирование на 3 взаимно
перпендикулярные плоскости
Прямоугольные проекции:
Наиболее распространены в конструкторской практике
Позволяют получить изображения, простые с точки зрения
графических построений
Обеспечивают точное соотношение размеров изображений
предметов на плоскости
15
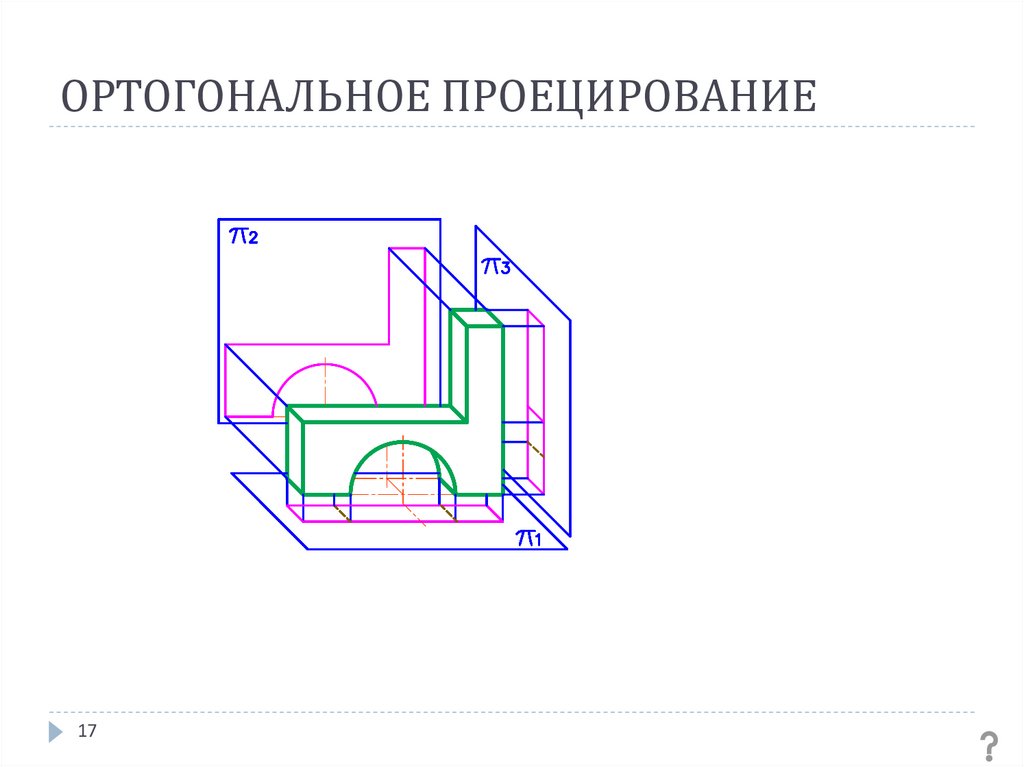
16. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
При ортогональном проецировании предметырасполагают относительно плоскостей проекций
таким образом, чтобы их основные измерения были
параллельны плоскостям проекций
При этом предмет находится между наблюдателем и
плоскостью проекций
16
17. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ
1718. ПОЛОЖЕНИЕ ТОЧКИ В ПРОСТРАНСТВЕ
Определение положения точек в пространствепроизводится по их прямоугольным проекциям на двух и
более плоскостях проекций
18
Слово «прямоугольный» часто заменяют словом
«ортогональный», образованным из слов
древнегреческого языка, обозначающих «прямой» и
«угол»
19. ДЕКАРТОВА СИСТЕМА КООРДИНАТНЫХ ОСЕЙ
Все пространственные объекты ориентируютотносительно пространственной декартовой системы
координатных осей – системы трех взаимно
перпендикулярных координатных плоскостей
19
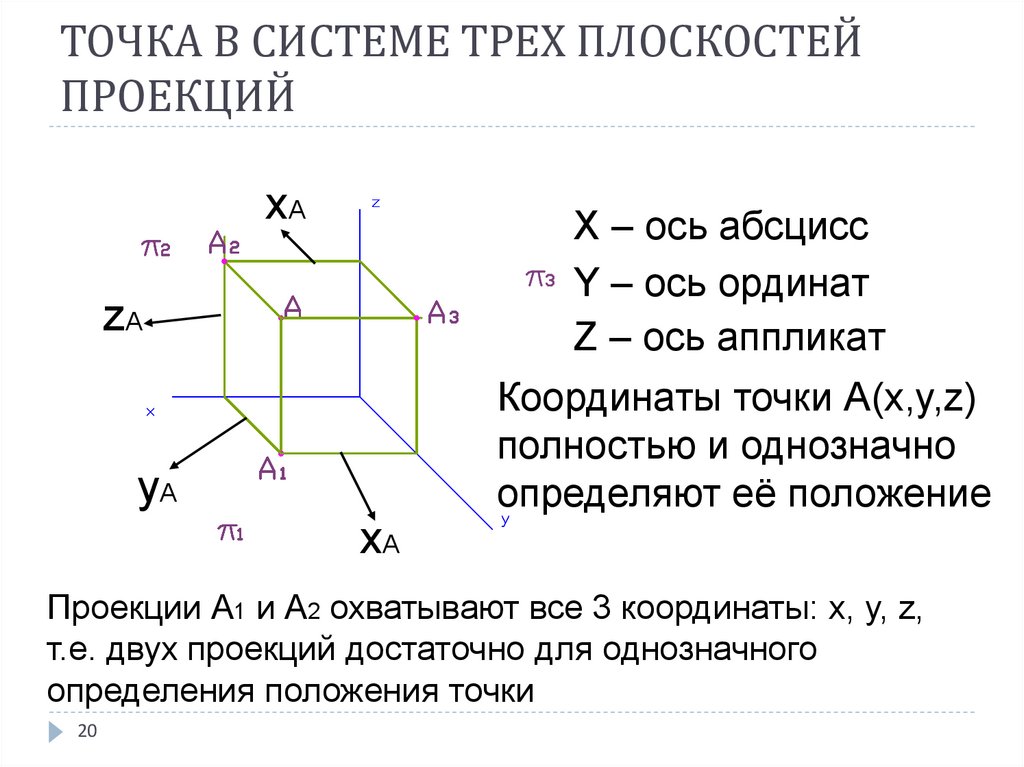
20. ТОЧКА В СИСТЕМЕ ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
xAX – ось абсцисс
Y – ось ординат
Z – ось аппликат
zA
Координаты точки А(x,y,z)
полностью и однозначно
определяют её положение
yA
xA
Проекции А1 и А2 охватывают все 3 координаты: x, y, z,
т.е. двух проекций достаточно для однозначного
определения положения точки
20
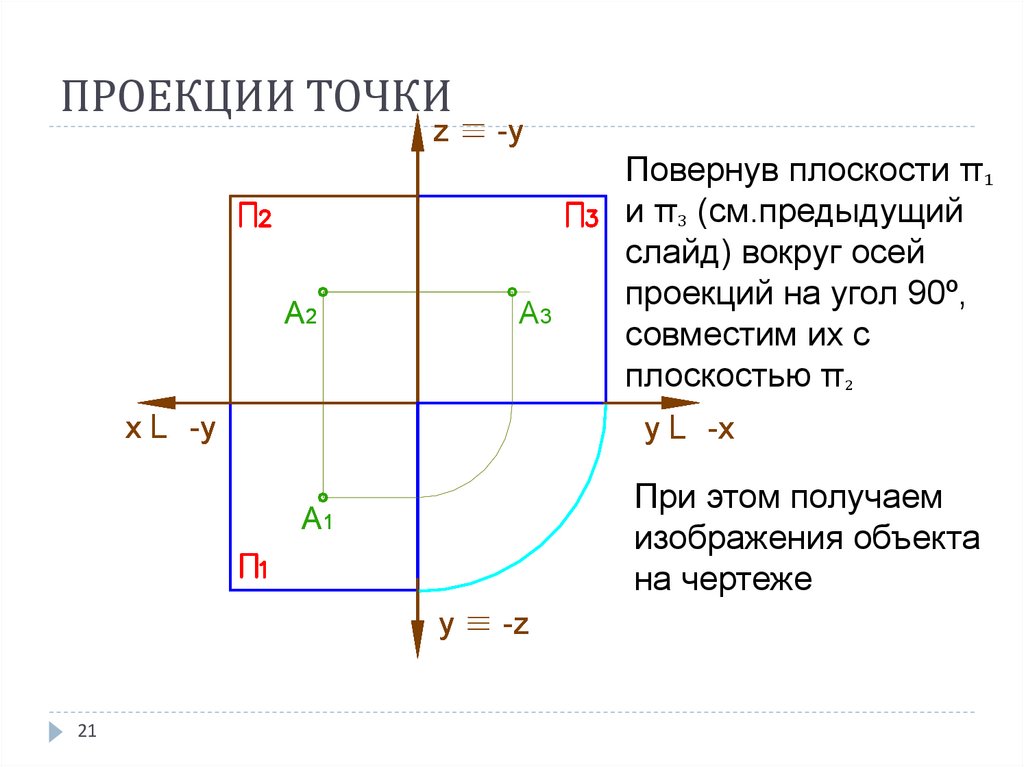
21. ПРОЕКЦИИ ТОЧКИ
zA2
-y
A3
x L -y
y L -x
При этом получаем
изображения объекта
на чертеже
A1
y
21
Повернув плоскости π₁
и π₃ (см.предыдущий
слайд) вокруг осей
проекций на угол 90º,
совместим их с
плоскостью π₂
-z
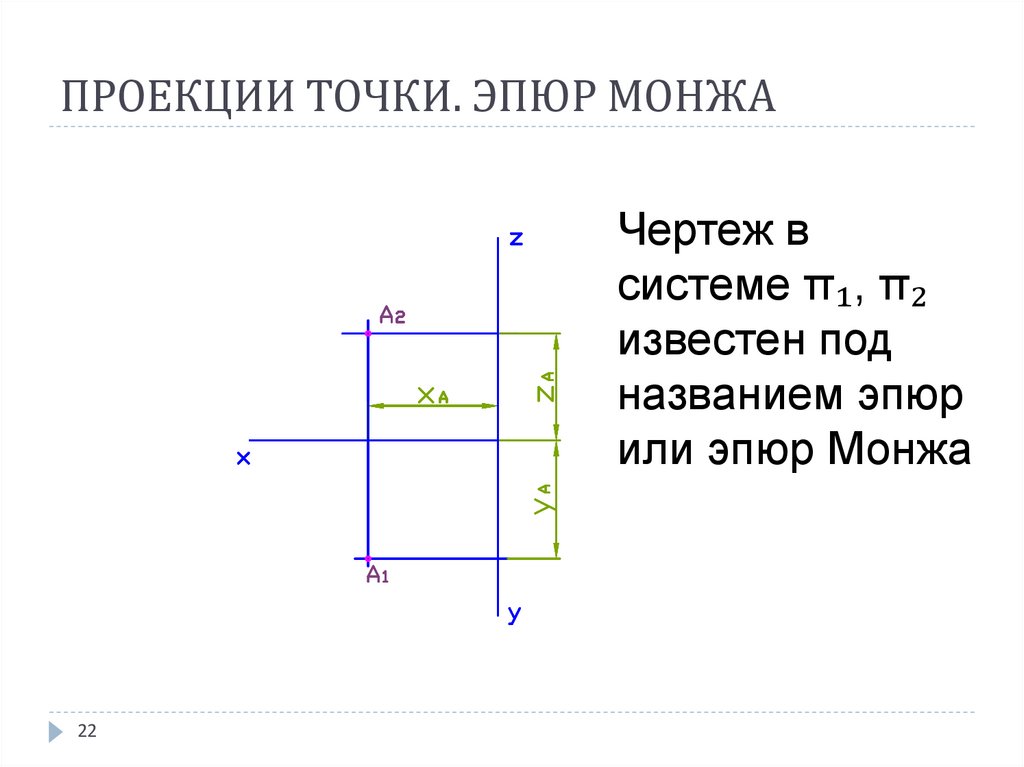
22. ПРОЕКЦИИ ТОЧКИ. ЭПЮР МОНЖА
Чертеж всистеме π₁, π₂
известен под
названием эпюр
или эпюр Монжа
22
23. ЧЕРТЕЖ
В дальнейшем эпюр Монжа, а также проекционныечертежи, в основе которых лежит метод Монжа,
будем называть одним словом - чертеж - и
понимать это слово только в указанном смысле. В
других случаях применения слова «чертеж» оно
будет сопровождаться соответствующим
определением (перспективный чертеж,
аксонометрический чертеж и т.п.) [3]
23
24. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
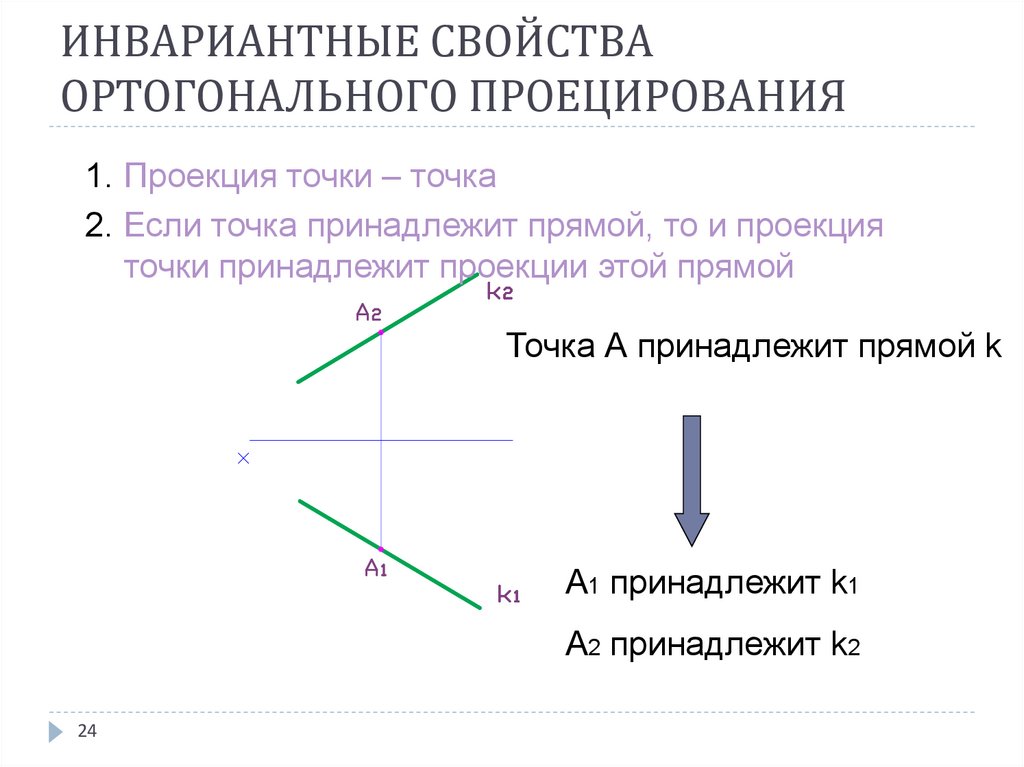
1. Проекция точки – точка2. Если точка принадлежит прямой, то и проекция
точки принадлежит проекции этой прямой
Точка А принадлежит прямой k
А1 принадлежит k1
А2 принадлежит k2
24
25. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
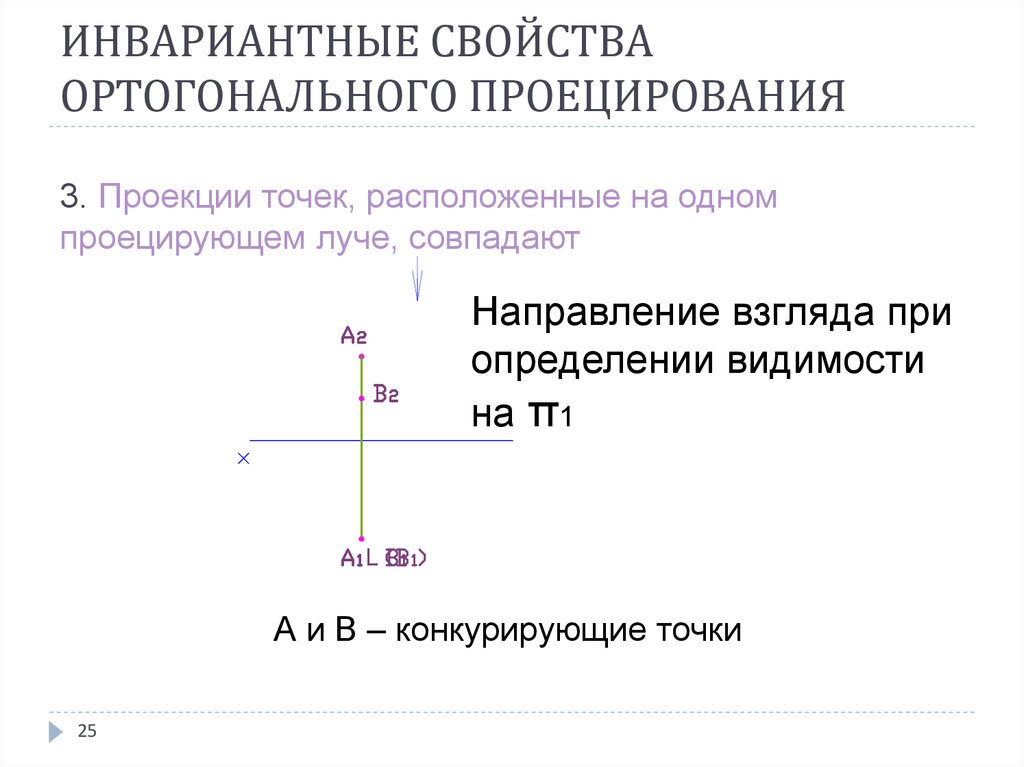
3. Проекции точек, расположенные на одномпроецирующем луче, совпадают
Направление взгляда при
определении видимости
на π1
L
А и В – конкурирующие точки
25
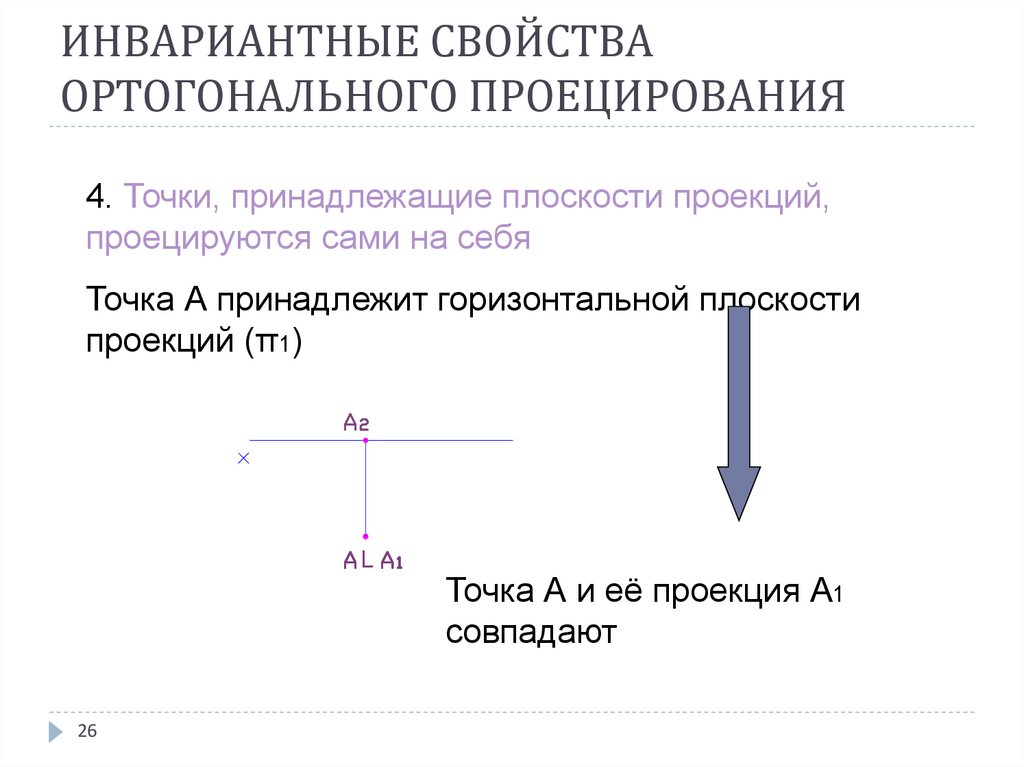
26. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
4. Точки, принадлежащие плоскости проекций,проецируются сами на себя
Точка А принадлежит горизонтальной плоскости
проекций (π1)
L
26
Точка А и её проекция А1
совпадают
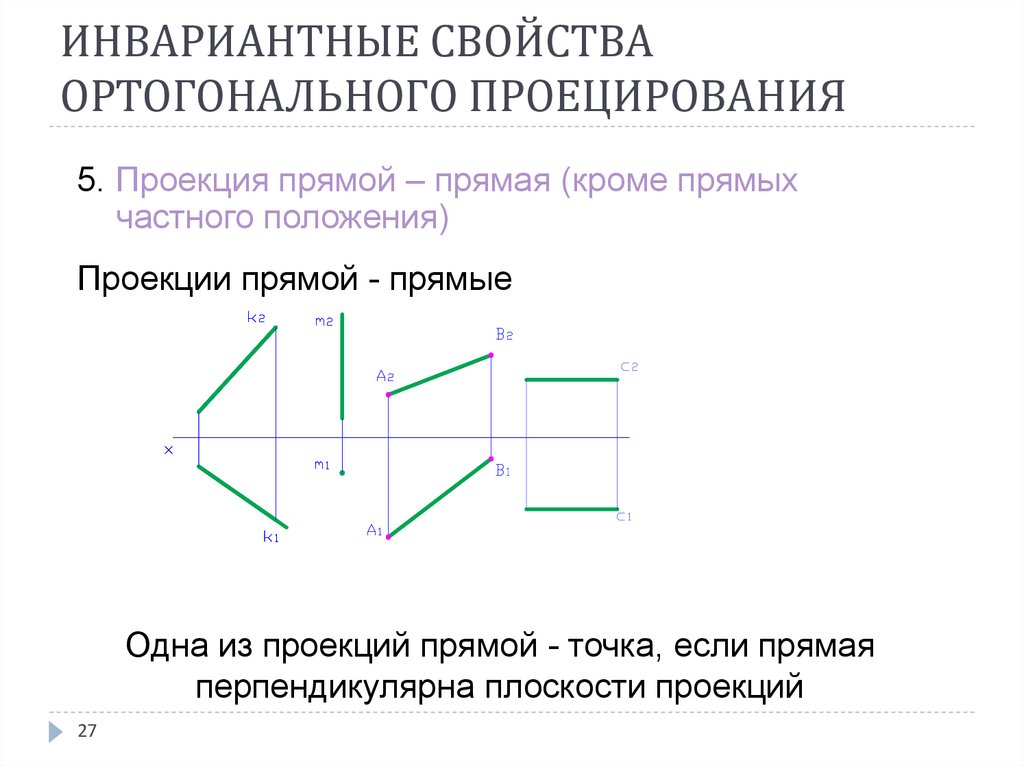
27. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
5. Проекция прямой – прямая (кроме прямыхчастного положения)
Проекции прямой - прямые
Одна из проекций прямой - точка, если прямая
перпендикулярна плоскости проекций
27
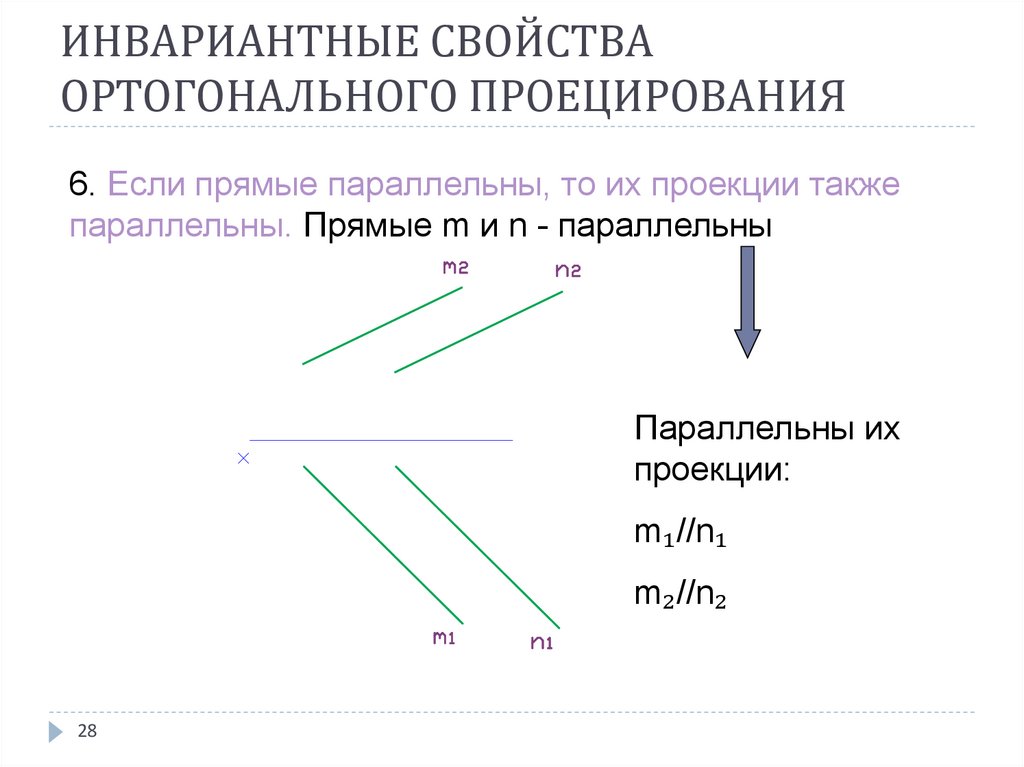
28. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
6. Если прямые параллельны, то их проекции такжепараллельны. Прямые m и n - параллельны
Параллельны их
проекции:
m₁//n₁
m₂//n₂
28
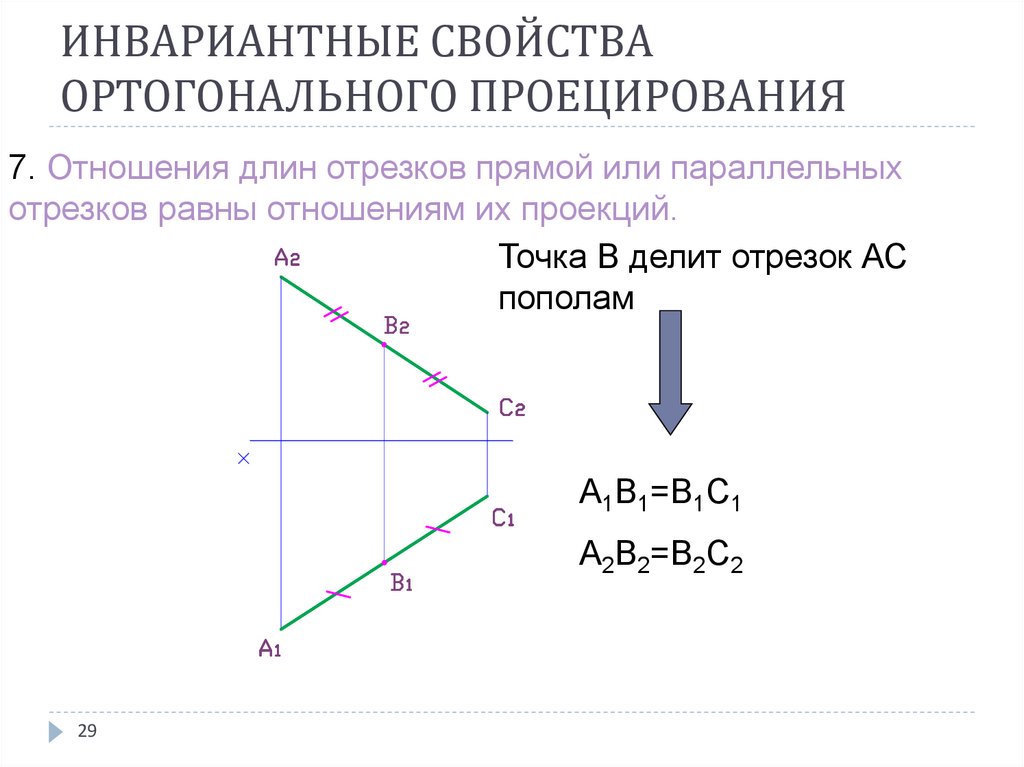
29. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
7. Отношения длин отрезков прямой или параллельныхотрезков равны отношениям их проекций.
Точка В делит отрезок АС
пополам
А1В1=В1С1
А2В2=В2С2
29
30. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
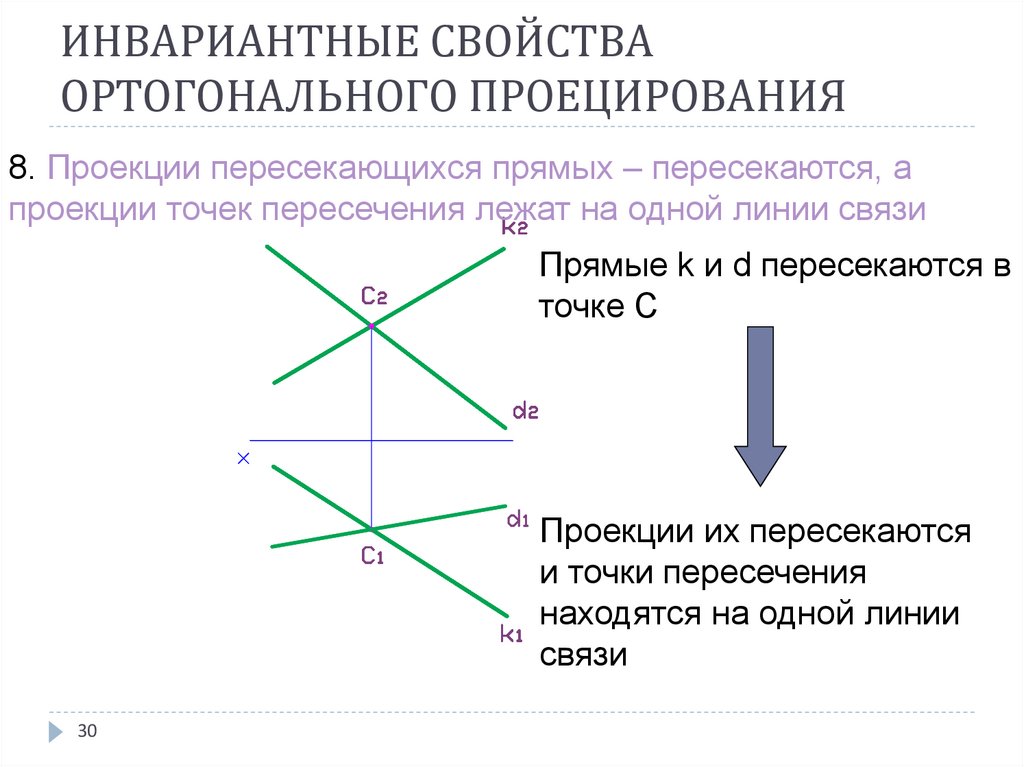
8. Проекции пересекающихся прямых – пересекаются, апроекции точек пересечения лежат на одной линии связи
Прямые k и d пересекаются в
точке С
Проекции их пересекаются
и точки пересечения
находятся на одной линии
связи
30
31. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
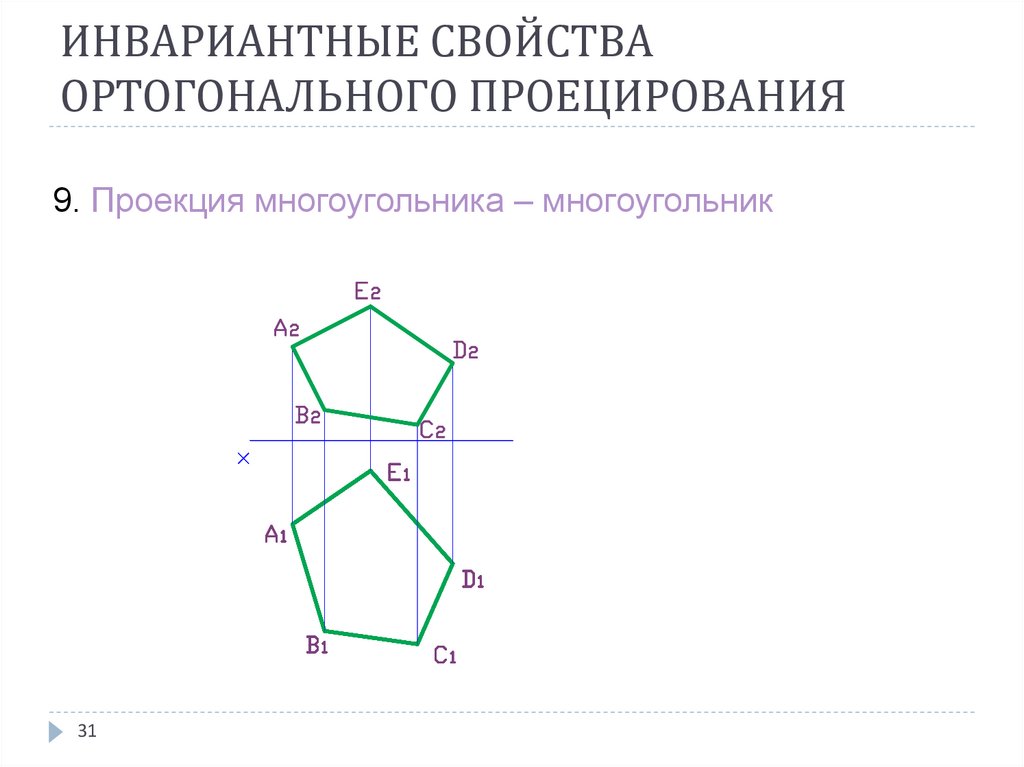
9. Проекция многоугольника – многоугольник31
32. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
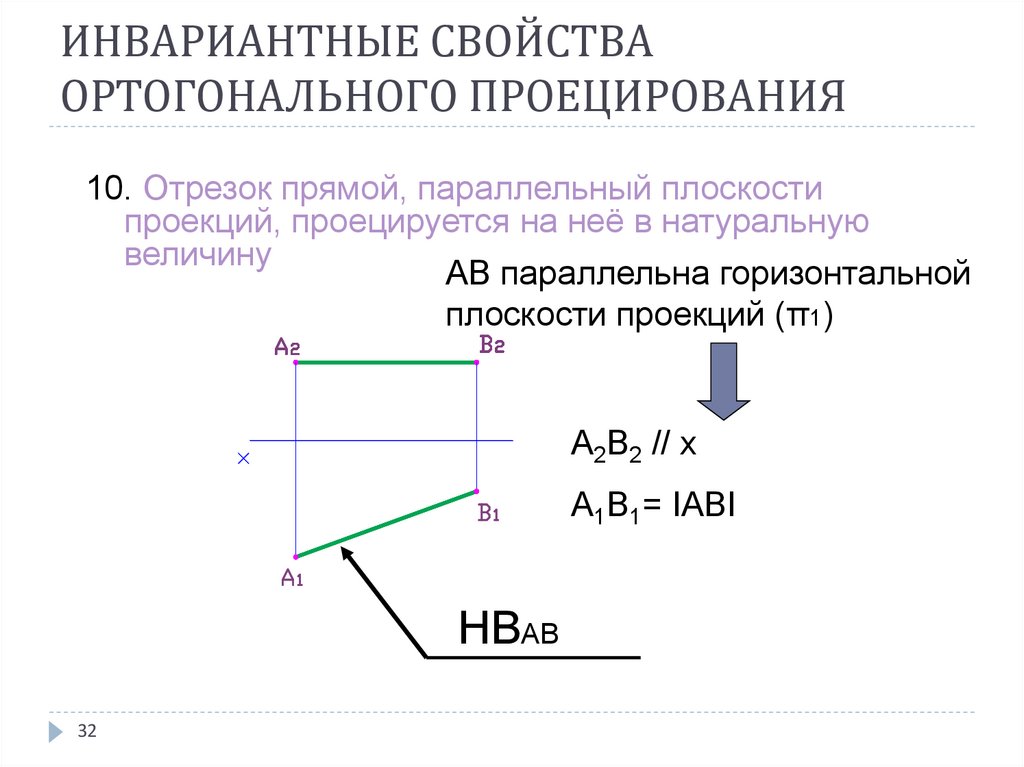
10. Отрезок прямой, параллельный плоскостипроекций, проецируется на неё в натуральную
величину
АВ параллельна горизонтальной
плоскости проекций (π1)
A2B2 // x
A1B1= IАВI
НВАВ
32
33. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
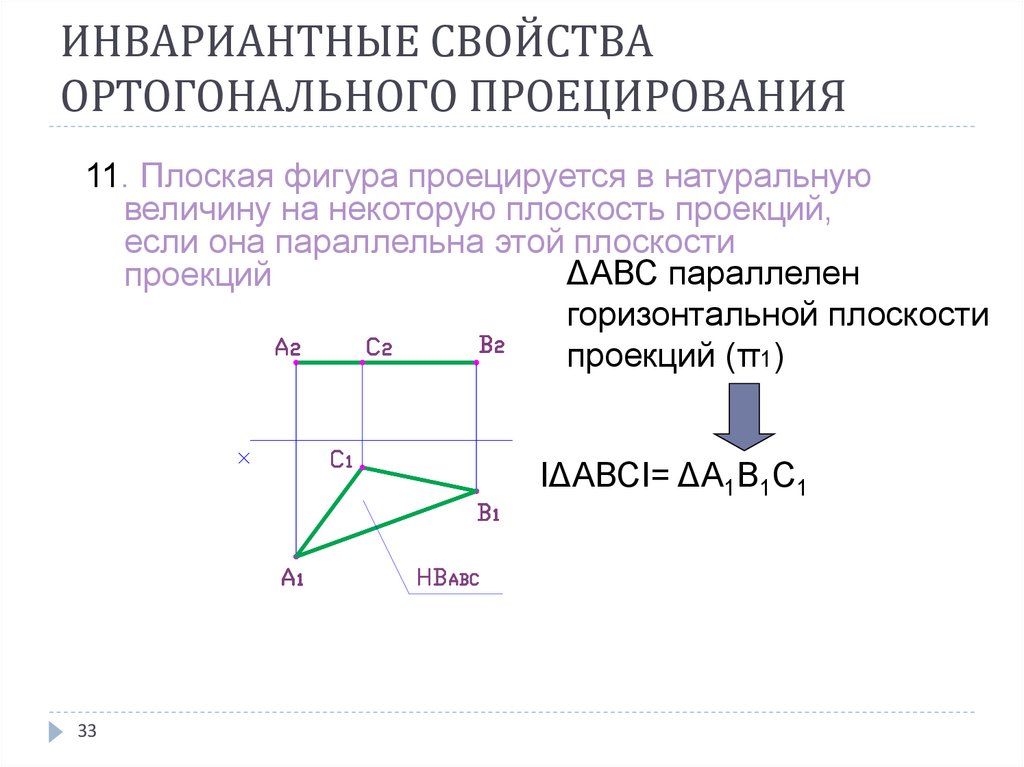
11. Плоская фигура проецируется в натуральнуювеличину на некоторую плоскость проекций,
если она параллельна этой плоскости
ΔАВС параллелен
проекций
горизонтальной плоскости
проекций (π1)
IΔАВСI= ΔА1В1С1
33
34. ИНВАРИАНТНЫЕ СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ
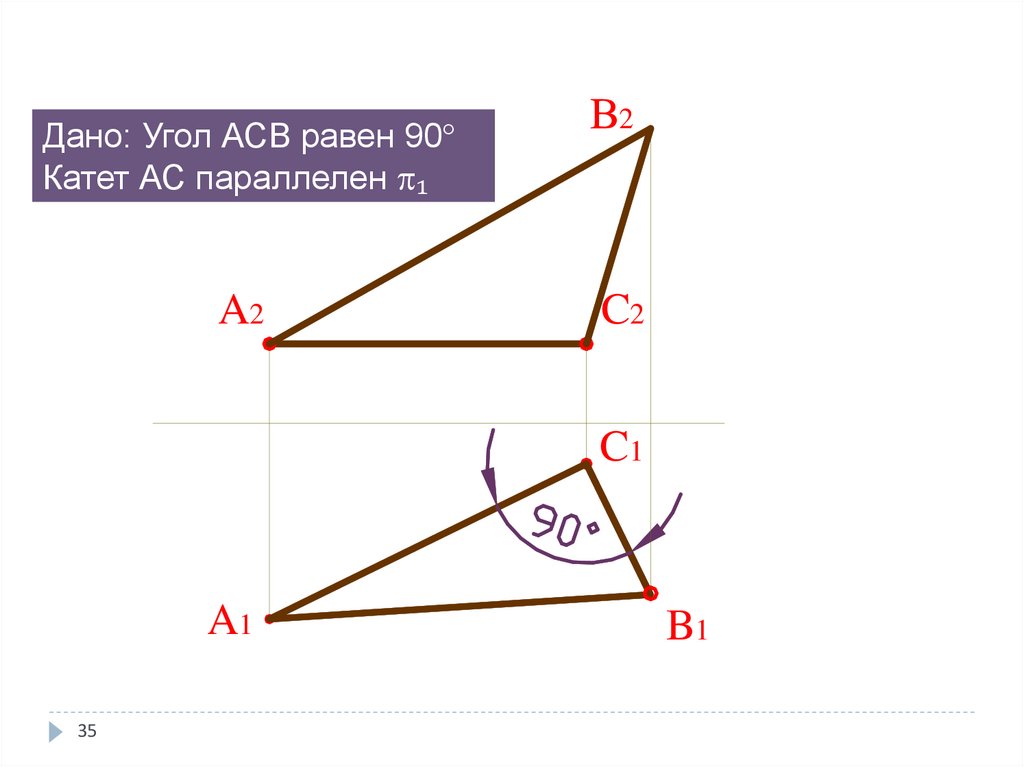
12. Прямой угол, у которого хотя бы один лучпараллелен плоскости проекций, проецируется на
неё в натуральную величину
34
35.
Дано: Угол АСВ равен 90°Катет АС параллелен ₁
2
A2
C2
C1
A1
35
B1
36. ВЫВОДЫ
Ортогональное проецирование – прямоугольное,параллельное проецирование на три взаимно
перпендикулярные плоскости – единственный
способ построения машиностроительных чертежей
36
37. ВЫВОДЫ
Положение точки определяется её ортогональнымипроекциями на две плоскости
По двум проекциям всегда можно построить третью
37




















 drafting
drafting








