Similar presentations:
Финансы, денежное обращение и кредит
1.
ФГБОУ ВО Новосибирский государственныйуниверситет экономики и управления
Дисциплина
Финансы, денежное
обращение и кредит
Кафедра финансового рынка и финансовых институтов
2.
Тема 3.1 Банковский кредит и егороль в экономике
Вопросы темы:
Процентная ставка: простые и сложные
проценты
Методы наращивания и дисконтирования
2
3.
Вопросы темы:Процентная ставка: простые и сложные проценты
Методы наращивания и дисконтирования
3
4.
Что из себя представляетпроцентная ставка?
В узком смысле
процентная ставка
представляет собой цену,
уплачиваемую за
использование заемных
денежных средств
4
5.
В более широком смысле,процентная ставка выступает:
•в
качестве измерителя уровня (нормы)
доходности
производимых
операций,
исчисляемого как отношение полученной
прибыли к величине вложенных средств и
выражаемого в долях единицы либо в
процентах
•в
качестве альтернативной стоимости
(издержек) капитала
5
6.
Простые процентыКак
правило,
простые
проценты
используются в краткосрочных финансовых
операциях, срок проведения которых меньше
или равен году
Базой для исчисления процентов за каждый период
в этом случае является первоначальная (исходная)
сумма сделки, которая НЕ ИЗМЕНЯЕТСЯ со
временем
6
7.
Сложные процентыСложной ставкой в экономике принято называть
величину, образующуюся при сложении прибыли с
основной суммой и участвующую в последующем
создании нового дохода
То есть по окончании каждого отчётного периода
(месяца, квартала, года) начисленный процент
суммируется с вкладом. Полученная сумма
выступает базисом для последующего образования
прибыли
То
есть
формула
обязательно
учитывает
капитализацию процентов
7
8.
Простыми словами:Каждый месяц банк прибавляет начисленные
проценты к депозиту. Таким образом размер тела
вклада, то есть расчетной базы, увеличивается
Через месяц банк начисляет процент уже на
бо́льшую сумму, то есть добавляет «процент на
процент». Чем чаще происходят начисления, тем
быстрее подрастет ваш капитал к окончанию срока
вклада
8
9.
Вопросы темы:Процентная ставка: простые и сложные
проценты
Методы наращивания и дисконтирования
9
10.
Сущность методовФинансовые сделки обычно связаны с предоставлением денег в
долг. Как правило, заемщик платит кредитору проценты за
пользование ссудой.
Методы
расчетов
денежных сумм
Наращение
Дисконтирование
Сущностью этих методов является приведение денежных
сумм, относящихся к различным временном периодам, к
требуемому моменту времени в настоящем или будущем.
10
11.
Метод наращенияЭкономический смысл метода наращения состоит в
определении величины, которая будет или может
быть получена из некоторой первоначальной
(текущей) суммы в результате проведения
операции
Другими словами, метод наращения позволяет
определить будущую величину (future value —
FV) текущей суммы (present value — PV) через
некоторый промежуток времени n, исходя из
заданной процентной ставки
11
12.
Наращение по простым процентам,если срок меньше года
В этом случае наращение по годовой ставке простых
процентов вычисляют по формуле:
FV = PV (1 + t/T * i)
где FV— будущая стоимость (величина)
PV — современная величина
i — процентная ставка деленная на 100
t — число дней проведения операции
T — временная база (число дней в году: 360, 365 или 366)
12
13.
Например_1В банке открыли депозит на сумму 100 000 руб. на
срок 240 дней по ставке 8%. Определить, какую
сумму вернет банк вкладчику по окончании срока
депозита и какой доход получит владелец депозита
Дано:
PV =
t=
T=
i=
Решение:
FV =
13
14.
Временная базаВ процессе проведения анализа в качестве
временной базы часто удобно использовать
условный, или финансовый, год, состоящий из 360
дней (12 месяцев по 30 дней). Исчисляемые по такой
базе проценты называют обыкновенными, или
коммерческими.
Точные проценты получают при базе, равной
фактическому числу дней в году, т. е. при T = 365 или
366.
14
15.
Например_ 1аПокупатель предоставил коммерческий кредит на
сумму 10 000 руб. через 30 дней. Ставка по кредиту
определена в размере 30% годовых. Какова будет
сумма оплаты по контракту?
Вычислим ее:
а) с использованием обыкновенных процентов
FV =
б) с использованием точных процентов
FV=
15
16.
Наращение по простым процентамна срок больше года
В общем случае наращение по годовой
ставке простых процентов вычисляют по
формуле:
FV = PV (1 + i * n)
где n — число периодов (лет)
16
17.
Например_2Открыли депозит на 100 000 рублей сроком
на 2 года по номинальной ставке 8%.
Банк использует метод простых процентов.
Дано:
PV =
i=
n=
Решение:
FV=
17
18.
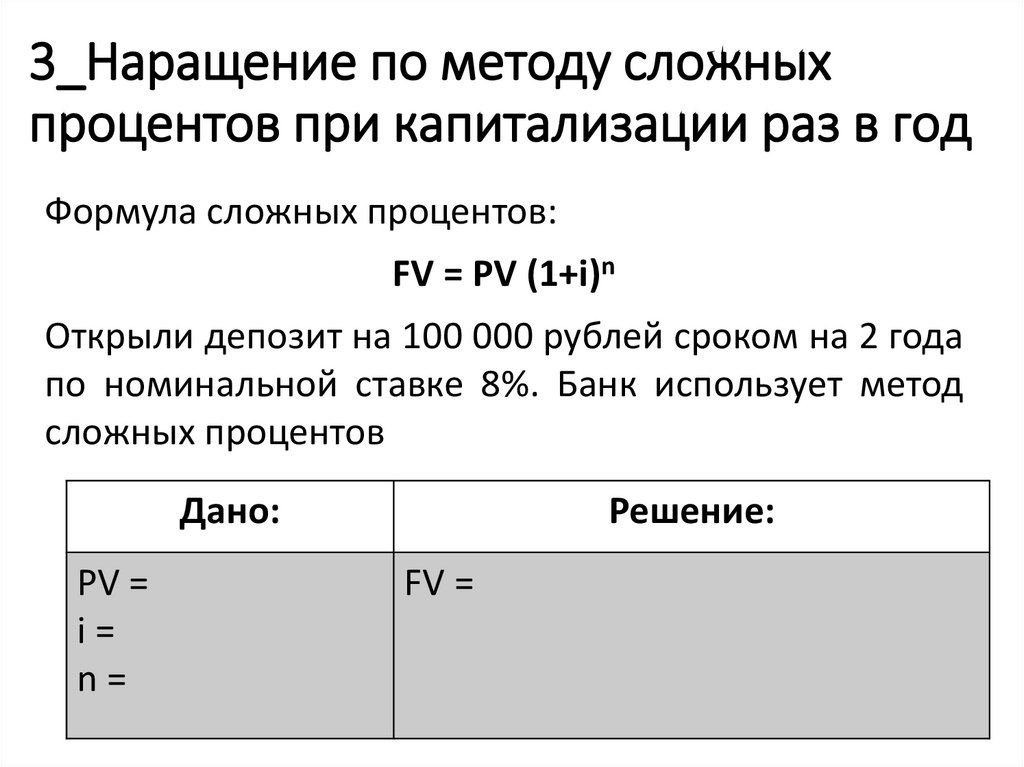
3_Наращение по методу сложныхпроцентов при капитализации раз в год
Формула сложных процентов:
FV = PV (1+i)n
Открыли депозит на 100 000 рублей сроком на 2 года
по номинальной ставке 8%. Банк использует метод
сложных процентов
Дано:
PV =
i=
n=
Решение:
FV =
18
19.
Наращение по методу сложных % скапитализацией несколько раз в год
Формула сложных процентов:
FV = PV (1+i/m)mn
где m – количество капитализаций в год
19
20.
Например_4Открыли депозит на 100 000 рублей сроком на 2
года по номинальной ставке 8%.
Банк использует метод сложных процентов с
капитализацией раз в полгода.
Дано:
PV =
i=
n=
m=
Решение:
FV =
20
21.
ДисконтированиеДисконтирование представляет собой процесс
нахождения денежной величины на заданный
момент времени по ее известному или
предполагаемому значению в будущем.
Дисконтирование является зеркальным отражением
наращения.
Следует отметить, что в зависимости от условий
проведения финансовых операций как наращение,
так и дисконтирование могут осуществляться с
применением простых и сложных процентов.
21
22.
ФормулыПростые проценты:
PV = FV / (1 + i * t/T)
PV = FV / (1 + i * n)
Сложные проценты:
PV = FV / (1 + i) n
PV = FV / (1 + i/m) nm
22
Разность FV — PV называют дисконтом, или скидкой
23.
Например_5Сколько нужно положить денежных средств на
вклад на 2 года под 10%, чтобы по истечению
срока вкладчик получил на руки около 150 000
руб. Банк использует метод сложных процентов с
капитализацией раз в год
Дано:
FV = 150 000
руб.
i = 0,1
n = 2 года
Решение:
PV =
23





















 finance
finance








