Обработка одномерных массивов

1. Обработка одномерных массивов

2.

Одномерный массив – упорядоченная последовательность однотипных
величин (в MathCAD необязательно), имеющих одно имя, но различающихся
индексами.
Индекс – это выражение целого типа, определяющее положение
отдельной величины в последовательности. Каждая отдельная величина
называется элементом массива.
Нумерация элементов в массиве с минимального значения индекса
(по умолчанию ORIGIN=1) до максимального значения индекса с шагом 1.

3.

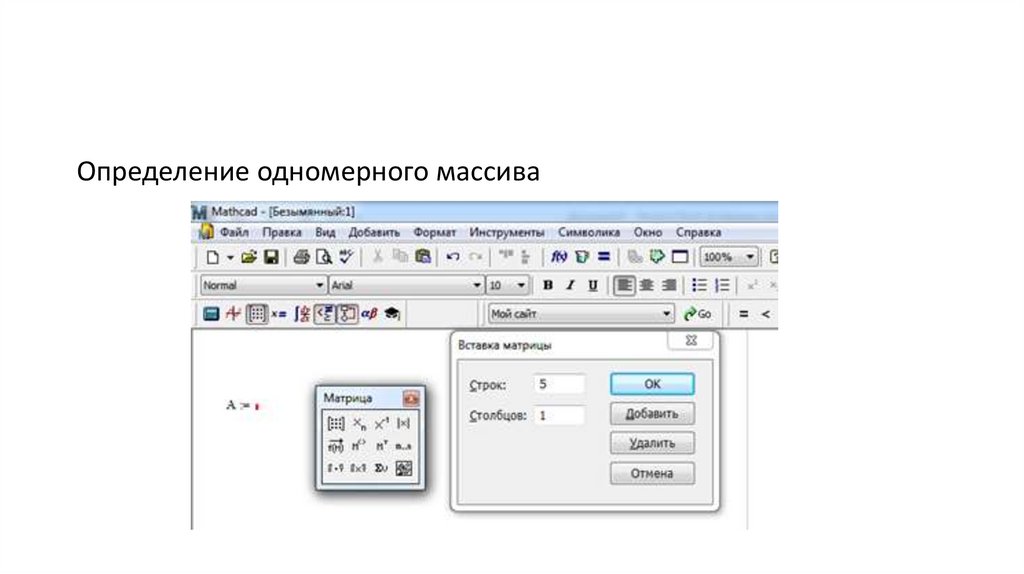
Определение одномерного массива

4. Действия над массивами ТИПОВЫЕ АЛГОРИТМЫ ОБРАБОТКИ ОДНОНОМЕРНЫХ МАССИВОВ

Вычислить сумму элементов массива А
ORIGIN := 1
sum1( X) :=
s 0
for i 1 .. rows( X)
s s+X
i
s
sum1( A) = 9
2
3
A := -1
0
5

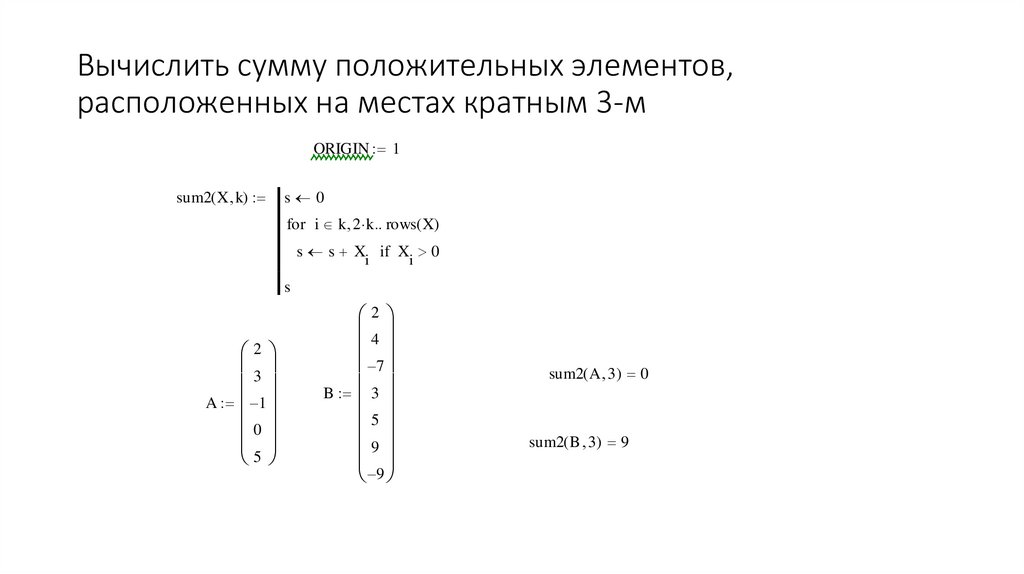
5. Вычислить сумму положительных элементов, расположенных на местах кратным 3-м

ORIGIN := 1
sum2( X , k) :=
s 0
for i k , 2 k .. rows( X)
s s + X if X > 0
i
i
s
2
3
A := -1
0
5
2
4
-7
B := 3
5
9
-9
sum2( A , 3 ) = 0
sum2( B , 3 ) = 9

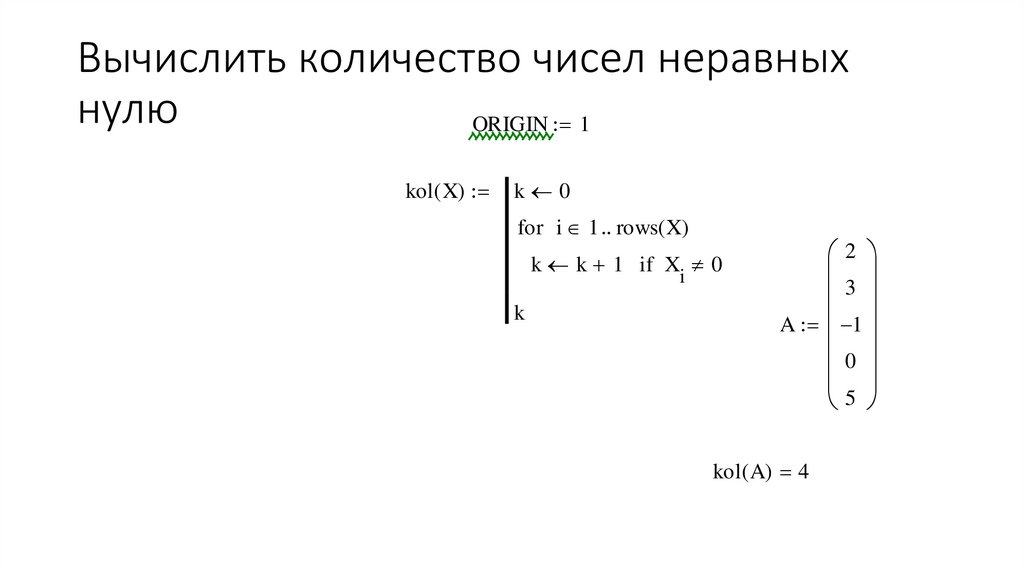
6. Вычислить количество чисел неравных нулю

ORIGIN := 1
kol( X) :=
k 0
for i 1 .. rows( X)
k k + 1 if X 0
i
k
2
3
A := -1
0
5
kol( A) = 4

7. Вычислить среднеарифметическое чисел принадлежащих отрезку [C,D]

ORIGIN := 1
sum4( X , C , D) :=
k 0
s 0
for i 1 .. rows( X)
(i ) (i )
if X C X D
k k+ 1
s s+X
i
s
0
-2
A := 3
-1
4
s
k
if k 0
"нет таких чисел" otherwise
sum4( A , 1 , 2 ) = "нет таких чисел"
sum4( A , 1 , 4 ) = 3.5

8. Вычислить произведение чисел одномерного массива

ORIGIN := 1
proiz( X) :=
p 1
for i 1 .. rows( X)
p p X
i
p
1
2
A := 3
4
5
proiz( A) = 120

9. Вычислить произведение отрицательных чисел одномерного массива, стоящих на нечетных местах

ORIGIN := 1
proiz2( X) :=
p 1
k 0
for i 1 , 3 .. rows( X)
if X < 0
i
p p X
i
k 1
p if k = 1
"нет таких чисел" otherwise
1
-2
A := 3
-4
2
-1
-4
B := 5
-2
-3
proiz2( A) = "нет таких чисел"
proiz2( B) = 3

10. Перестановка элементов массива местами

Пусть дан массив из n чисел. Необходимо поменять местами два элемента местами , стоящих
на позиции к и m соответственно.
Рассмотрим тестовый пример.
Пусть количество элементов n=5
Х:
3
7
Х1
5
Х2
4
Х3
9
Х4
Х5
Зададим к и m. Пусть k=2; m=5. Необходимо получить преобразованный массив вида:
Хпреоб:
3
9
5
4
7
Чтобы добиться такого результата необходимо решить классическую задачу «о трех стаканах».
Для этого вводиться пустой стакан Х_ТМР.

11.

ORIGIN := 1
obmen ( X , k , m) :=
if ( k rows( X) ) ( m rows( X) ) ( m > 0 ) ( k > 0 )
X_tmp X
k
X X
k
m
X X_tmp
m
X
"Выход за границы массива" otherwise
3
7
A := 5
4
9
3
9
obmen ( A , 2 , 5 ) = 5
4
7
obmen ( A , 6 , 1 ) = "Выход за границы массива"
obmen ( A , 3 , -3 ) = "Выход за границы массива"

12. Поиск минимального и максимального элемента массива

Пусть дан массив из n чисел. Необходимо найти самый наименьший элемент
массива и его порядковый номер.
Алгоритм.
Предположим, что минимальный элемент массива – это самый первый элемент, а
следовательно его порядковый номер равен 1. Хранить значение минимального будет,
например, в переменной X_MIN, которая имеет тот же тип, что и элементы массива;
порядковый номер, минимального элемента будет хранить в переменной целого типа –
n_min.
Оставшиеся n-1 (х2, х3, …, xn) элементов сравниваются с минимальным элементом
x_min. При сравнении можно использовать знаки а)< и б)<=.
Если окажется, что xi – элемент, меньше x_min, то то минимальным становится этот элемент, а
порядковый номер равен i. Переходим к сравнению следующего элемента и так далее, до тех
пор пока есть, что сравнивать.

13.

Примечание 1. Если при поиске минимального элемента в сравнении участвует строгий знак
“<”, то находится самый первый (левый) минимальный элемент; если не строгий знак “<=”, то
находится самый последний (правый) минимальный элемент массива.
Примечание 2. При поиске максимального элемента алгоритм аналогичен, поиску
минимального элемента, за исключением знаков сравнения >, >=. . Если при поиске
максимального элемента в сравнении участвует строгий знак “>”, то находится самый первый
(левый) максимальный элемент; если не строгий знак “>=”, то находится самый последний
(правый) максимальный элемент массива

14. Поиск самого левого минимального элемента

ORIGIN := 1
poisk_min( X) :=
x_min X
1
n_min 1
for i 2 .. rows( X)
if X < x_min
i
x_min X
i
n_min i
z x_min
1
z n_min
2
z
3
4
A := 3
5
7
A_min := poisk_min( A)
n_min
A_min = 3
n_min = 1

15. Поиск самого правого минимального элемента

ORIGIN := 1
poisk_min( X) :=
x_min X
1
n_min 1
for i 2 .. rows( X)
if X x_min
i
x_min X
i
n_min i
z x_min
1
z n_min
2
z
3
4
A := 3
5
7
A_min := poisk_min( A)
n_min
A_min = 3
n_min = 3

16. Самый правый максимальный элемент поменять местами с элементом с указанным номером

ORIGIN := 1
obmen_max( X , k) :=
if ( k rows( X) ) ( k > 0 )
x_max X
1
n_max 1
for i 2 .. rows( X)
if X x_max
i
x_max X
i
n_max i
X
n_max
X
k
X x_max
k
X
"указанный номер превышает размер массива" otherwise
5
1
A := 5
3
4
5
1
obmen_max( A , 5 ) = 4
3
5
obmen_max( A , 7 ) = "указанный номер превышает размер массива"
obmen_max( A , -7 ) = "указанный номер превышает размер массива"

17. ФОРМИРОВАНИЕ НОВЫХ МАССИВОВ

Задача
формулируется следующим образом: Дано несколько
массивов. Из элементов этих массивов сформировать новый массив.

18. Сформировать новый из положительных элементов, стоящих на четных местах, первого массива и элементов второго массива,

расположенных после правого
максимального элемента
ORIGIN := 1
new_array( X , Y) :=
k 0
for i 2 , 4 .. rows( X)
if X > 0
i
k k+1
Z X
k
i
max_Y Y
1
n 1
for i 1 .. rows( Y)
if Y max_Y
i
max_Y Y
i
n i
for i n + 1 .. rows( Y) if n rows( Y)
k k+1
Z Y
k
i
Z if k 0
"Массив не создан. Пустой" otherwise

19.

2
-1
A := 3
4
0
0
-1
C := -9
0
-4
8
2
7
B := 5
8
2
6
2
3
D := 4
5
5
4
new_array( A , B) = 2
6
new_array( C , D) = "Массив не создан. Пустой"