Similar presentations:
Дискретная математика. Отношения
1.
Дискретная математикаПреподаватель:
проф. Иванилова Татьяна Николаевна
2.
Соответствия◦ Пусть заданы множества X и Y.
◦ Соответствие - это множество пар вида <x,y>,
образующихся при сопоставлении элементов
множества X элементам множества Y, и сами
сопоставляемые множества X и Y.
q = (X, Y, Q),
Q X Y.
◦ ПрАQ A называется областью определения
соответствия, или источником соответствия.
◦ ПрВQ В называется областью значений
соответствия, или приемником.
3.
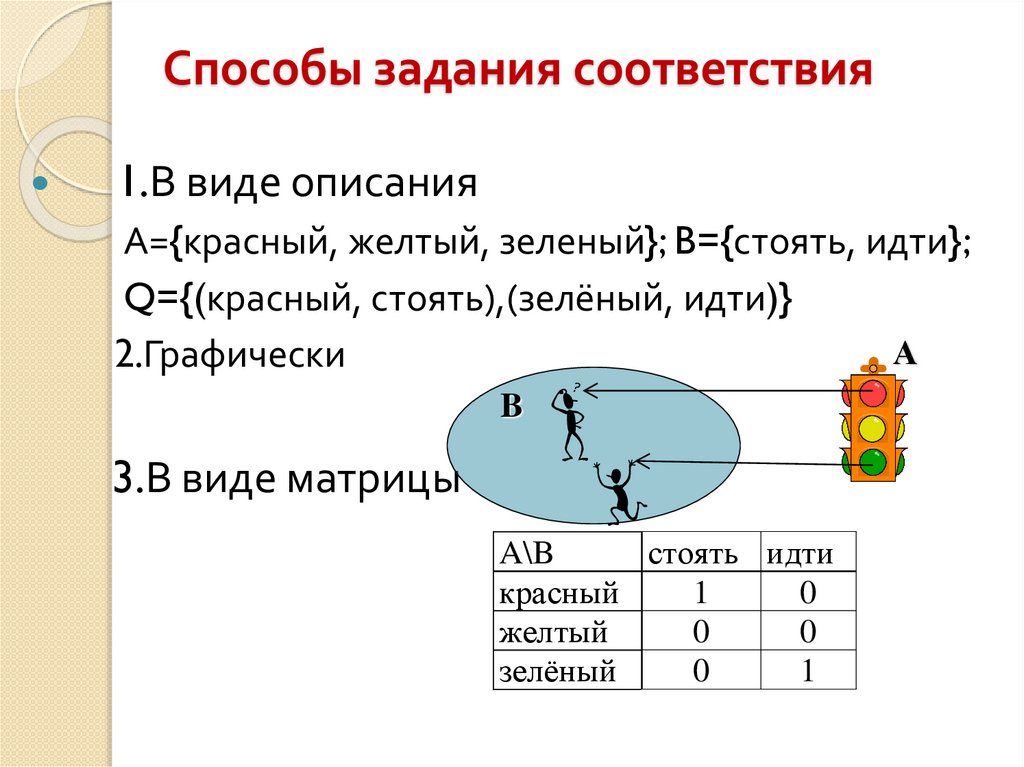
Способы задания соответствия1.В виде описания
А={красный, желтый, зеленый}; B={стоять, идти};
Q={(красный, стоять),(зелёный, идти)}
А
2.Графически
B
3.В виде матрицы
A\B
стоять идти
красный
1
0
желтый
0
0
зелёный
0
1
4.
Отношения• Термин «отношение» обозначает
некоторые виды соответствий, заданные на
одном множестве.
• Если задано соответствие (Х,ρ), то об
элементе у ρ(х) говорят, что он находится
в отношении ρ к элементу х: хρу.
• Отношением называется ρ Хn
ρ = {<x1,…, xn >| xi ρ xj ; xi, xj X}
5.
• Элементами множества Хn являютсяупорядоченные n-ки, и такое отношение
называют n-арным или n-местным;
• Множество упорядоченных пар элементов
называют бинарным, упорядоченных троек тернарным.
• Бинарным (двухместным) отношением ρ
называется множество упорядоченных пар,
элементы которых связаны некоторой
зависимостью.
ρ = {<x,y>| x,y X, хρу}
6.
Отношения• Областью определения бинарного отношения
называется:
Dρ = {x y хρу }.
• Областью значений бинарного отношения
называется:
Rρ = {у х хρу }.
• Пример:
ρ1 = {<х, у> х, у R x = у}, отношение равенства на
множестве действительных чисел, Dρ = Rρ= R.
ρ2 = {<x,y> | x, y – люди, x младше y}, отношение «Быть
младше» на множестве людей.
• Любое отношение ρ – подмножество прямого
произведения некоторых множеств Х и Y , то есть
ρ X Y, причем
Dρ Х, Rρ Y.
7.
ОтношенияЕсли ρ A2 - отношение, заданное на множестве А, то
• Обратное отношение
ρ -1={<a,b> | <b,a> ρ }
• Дополнение отношения ρ ={<a,b> | <a,b> ρ }
• Тождественное отношение I = {<a,a> | a A}
• Композицией отношений ρ1, ρ2 называется
отношение:
ρ1◦ρ2 = {<a, c> b| <a, b> ρ1, <b, c> ρ2}.
8.
Примеры:1. ρ1 = {<х, у> х, у R у = x2 },
ρ1-1 = {<х, у> х, у R x = y2 };
2. ρ2 = {<1,2>, <2,2>, <3,4>, <4,2>},
ρ2-1 = {<2,1>, <2,2>, <4,3>, <2,4>};
3. ρ2◦ρ2-1= {<1,1>,<1,2>,<1,4>,<2,1>,<2,2>,
<2,4>,<3,3>,<4,1>,<4,2>,<4,4>}
9.
Cвойства бинарных отношенийкоторые выполняются при использовании
операций расчета обратных отношений и
композиции:
(ρ-1)-1 = ρ
(ρ1◦ρ2)-1 = ρ2-1◦ρ1-1
10.
Специальные бинарныеотношения
• Отношение ρ на множестве Х называют
рефлексивным, если х Х выполняется хρх.
• Отношение ρ на множестве Х называется
симметричным, если х,у Х из хρу уρх.
• Отношение ρ на множестве Х называется
транзитивным, если х,у,z X из хρу, уρz
хρz.
• Отношение ρ на множестве Х называется
антисимметричным, если
х,у Х из хρу и уρх у = х.
11.
Пример1. Отношение x<y.
ρ1 = {<х, у> х, у R x < у}
Рефл. х Х <x,x> ρ1 , т.к. x < x – не выполняется, ρ1
не рефлексивно,
Симм. х,у Х если <x,y> ρ1, то <y,x> ρ1.
в нашем случае: если x < у , то тогда не выполняется
что у < x, ρ1 не симметрично,
Транзит. х,у,z X из <x,y> ρ1, <y,z> ρ1
<x,z> ρ1.
В нашем случае: если x < у и y < z, то x < z –
выполняется, ρ1 - транзитивно
12.
Специальные бинарные отношения• Рефлексивное, симметричное, транзитивное
отношение на Х называется отношением
эквивалентности на множестве Х.
• Пример:
Отношение равенства на множестве целых чисел
ρ1 = {<х, у> х, у Z x = у}
Рефлексивно: x=x
Симметрично: если x=y то y=x
Транзитивно: если x=y, y=z, то x=z
Следовательно ρ1 отношение эквивалентности.
13.
Пусть ρ – отношение эквивалентности на Х.Классом эквивалентности, порожденным элементом х,
называется подмножество Х, состоящее из тех элементов
у Х, для которых хρу: [x] = {y у Х и хρу}.
Примеры:
1.Отношение равенства на множестве целых чисел
порождает классы эквивалентности, состоящие из одного
элемента x Z [x] = {x}.
2. Для отношения принадлежности к одной студенческой
группе:
ρ = {<х, у> х, у студенты x и у учатся в одной
группе}
классом эквивалентности считается множество
студентов одной группы: [x]={y | y учится с x в одной
группе}
14.
Теорема 1• Пусть ρ – отношение эквивалентности
на множестве Х, тогда
– если х Х, то х [x]
– если х, y Х и xρy, то [x] = [y]
15.
Разбиение множества Х• Разбиением множества Х называется
совокупность попарно непересекающихся
подмножеств Х таких, что любой элемент Х
принадлежит одному и только одному из
этих подмножеств.
Пример:
Х = {1, 2, 3, 4, 5}. Тогда {{1, 2}, {3, 4}, {5, 6}} –
разбиение Х.
16.
Теорема 2Любое отношение эквивалентности ρ
определяет разбиение множества Х на
классы эквивалентности относительно
этого отношения
17.
ПримерПусть ρ – отношение сравнимости по
модулю mod.
ρ = {<х, у> х, у A у = x±mod*n, n=0,1,2,…}
Пусть A={ 5,6,7,8,9,10}, mod=2
тогда ρ = {<х, у> х, у A у = x±2*n,
n=0,1,2,…}
[5]={5,7,9} [6]={6,8,10}
Разбиение A={[5], [6]}
18.
Специальные бинарные отношенияРефлексивное, антисимметричное, транзитивное отношение
называется отношением частичного (нестрогого) порядка
на множестве Х.
Примеры:
1. ρ = {{<х, у> |x, y N x ≤ y} – отношение частичного
порядка
Рефлексивно: x ≤ x,
антисимметрично: нет ни одного случая симметричных пар,
транзитивно: x ≤ y, y≤ z, x ≤ z
2. Схема организации подчинения в учреждении –
отношение частичного порядка на множестве должностей.
Отношение частичного порядка на Х, для которых любые два
элементы сравнимы
( х,у Х либо х ρ у или у ρ х),
называется отношением линейного порядка.
19.
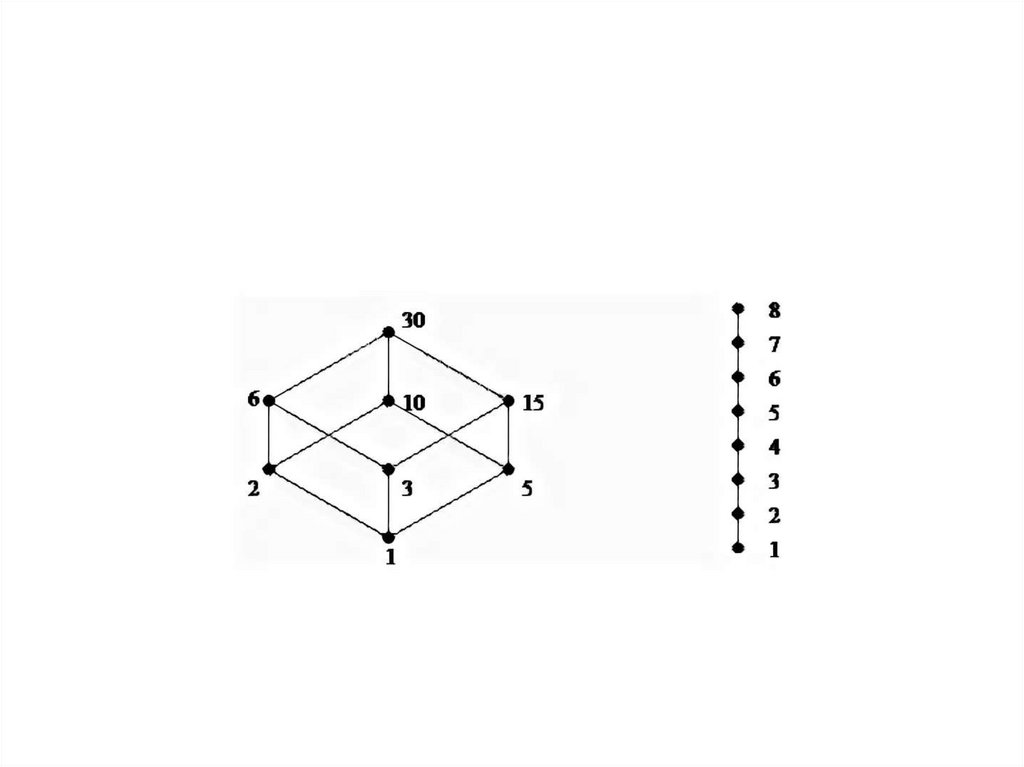
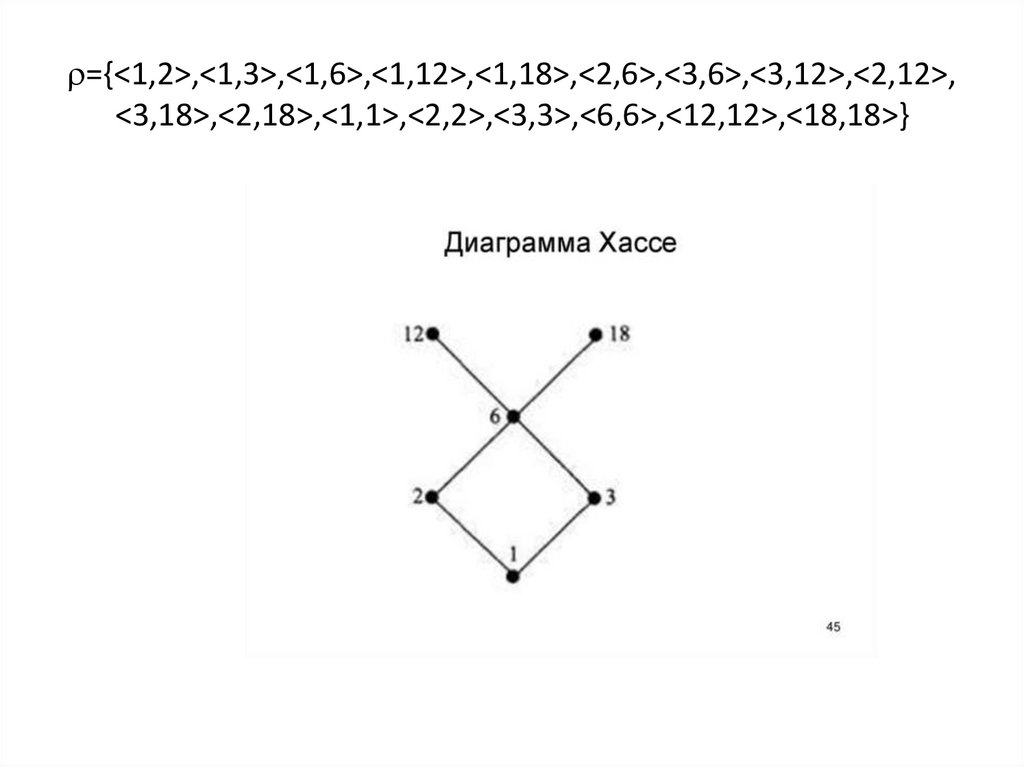
Диаграмма Хассе• Отношение частичного или линейного
порядка можно изобразить на диаграмме
Хассе таким образом:
• Каждый элемент множества изображается
точкой. И если в отношении есть пара <x,y>,
то x изображается ниже y и соединяется с y
одним или несколькими отрезками.
20.
21.
={<1,2>,<1,3>,<1,6>,<1,12>,<1,18>,<2,6>,<3,6>,<3,12>,<2,12>,<3,18>,<2,18>,<1,1>,<2,2>,<3,3>,<6,6>,<12,12>,<18,18>}


















 mathematics
mathematics