Similar presentations:
Структуры и алгоритмы обработки данных. Поиск в тексте. Постановка задачи (лекция 3)
1.
1Структуры и алгоритмы обработки данных
(часть 2)
Лекция 3
Москва 2023
2.
2Поиск в тексте. Постановка задачи
Дано:
• Некоторый текст Т (haystack) и образец или шаблон W
(needle) – тоже текст (подстрока)
• Или формально: Пусть заданы массивы Т и W из n и m
символов соответственно, причем 0<m≤n
• Элементы массивов Т и W – символы некоторого конечного
алфавита – например:
{0, 1}, или {a, …, z}, или {а, …, я}.
Результат:
• Найти первое слева вхождение этого образца в указанный
текст, т.е. сообщить о нахождении и, возможно, вернуть
индекс, начиная с которого образец присутствует в тексте.
3.
3Линейный (последовательный, прямой) поиск
Примитивный, наивный алгоритм
(англ. brute force algorithm)
Пример:
Требуется найти все вхождения образца W = abaa в тексте T = abcabaabcabca
Тогда:
Со сдвигом S от 0 до │T│ – │W│ посимвольно сравниваются T и W
Результат:
Образец входит в текст со сдвигом S=3, индекс i=4:
Здесь и далее сдвиг образца – не физический в памяти, а приращение значения индексной
переменной.
4.
4Псевдокод алгоритма прямого поиска
justFindStr (char *T, char *W) do
//i – индекс в строке T, j – индекс в подстроке W, lT – длина T, lW – длина W
//f – индекс начала возможного вхождения
i ← 1, j ← 1, f, lT ← length(T), lW ← length(W);
if (lT < lW) возврат -1;
while (i ≤ lT-lW+1) //сдвиг по строке T не дальше, чем lT - lW
do
f ← i; //начальный индекс возможного вхождения
while ((j≤lW) and (T[i]==W[j])) do //сравнение до конца образца
i ← i+1; j ← j+1;
od
if (j = lW+1) возврат f; // удачный поиск
j ← 1; i ← f+1; //сдвиг++ и возврат к началу подстроки
od
возврат -1; // неудачный поиск
od
5.
5Временная сложность алгоритма прямого поиска подстроки
• Худший случай – обнаружение образца W→{A….AB} длиной │W│=m в конце
текста T→{AAA….AAAB} длиной │T│=n;
• для обнаружения совпадения в конце строки потребуется произвести порядка
n·m сравнений, то есть O(n·m).
Недостатки наивного алгоритма:
1. Как алгоритм «грубой силы», он отличается высокой сложностью: O(n·m) в
худшем, О(n-m+1) в лучшем, О(2·n) в среднем случае.
2. После несовпадения просмотр всегда начинается с первого символа W. Если
образец читается из внешней памяти, то такие возвраты занимают недопустимо
много времени.
3. Информация о тексте T, получаемая при проверке с очередным сдвигом, никак
не учитывается при проверке последующих сдвигов.
6.
6Улучшение эффективности поиска подстроки:
Цель улучшений - по возможности при поиске сдвигать
образец больше, чем на одну позицию, что, в конечном счёте,
потребует меньшего числа посимвольных сравнений.
Механизм – препроцессинг – это предварительная обработка
образца, позволяющая учесть частичные совпадения с текстом.
Реализации:
• алгоритм Кнута-Морриса-Пратта,
• алгоритм Бойера-Мура,
• алгоритм конечного автомата.
7.
7Алгоритм Кнута-Морриса-Пратта
Hoola-Hoola girls like Hooligans.
Hooligan
Hooligan
8.
8Алгоритм Кнута-Морриса-Пратта
Hoola-Hoola girls like Hooligans.
Hooligan
Hooligan
Hooligan
9.
9Алгоритм Кнута-Морриса-Пратта
Hoola-Hoola girls like Hooligans.
Hooligan
10.
10Алгоритм Кнута-Морриса-Пратта
Hoola-Hoola girls like Hooligans.
Hooligan
11.
11Алгоритм Кнута-Морриса-Пратта
Дональд Эрвин Кнут
(родился в 1938 году)
Джеймс Хайрам Моррис
(родился в 1941 году)
Вон Рональд Пратт
(родился в 1941 году)
Первое упоминание в 1970 году.
Donald Knuth; James H. Morris, Jr, Vaughan Pratt. Fast pattern matching in strings // SIAM
Journal on Computing: journal. — 1977. — Vol. 6, no. 2. — P. 323—350.
12.
12Алгоритм Кнута-Морриса-Пратта
Независимо друг от друга, в 1969 году Матиясевич обнаружил
аналогичный алгоритм, закодированный двумерной машиной
Тьюринга, при изучении задачи распознавания сопоставления
строк с образцом над двоичным алфавитом. Это был первый
алгоритм сопоставления строк с линейным временем
Ю́рий Влади́мирович
Матиясе́вич
13.
13Алгоритм Кнута-Морриса-Пратта
Этапы работы алгоритма КМП:
1. Формирование массива , используемого при сдвиге образа вдоль
строки;
2. Поиск образа в строке.
Префикс-функция:
Префикс-функция для i-го символа образа возвращает некоторое
значение.
Это значение будем хранить в [i].
14.
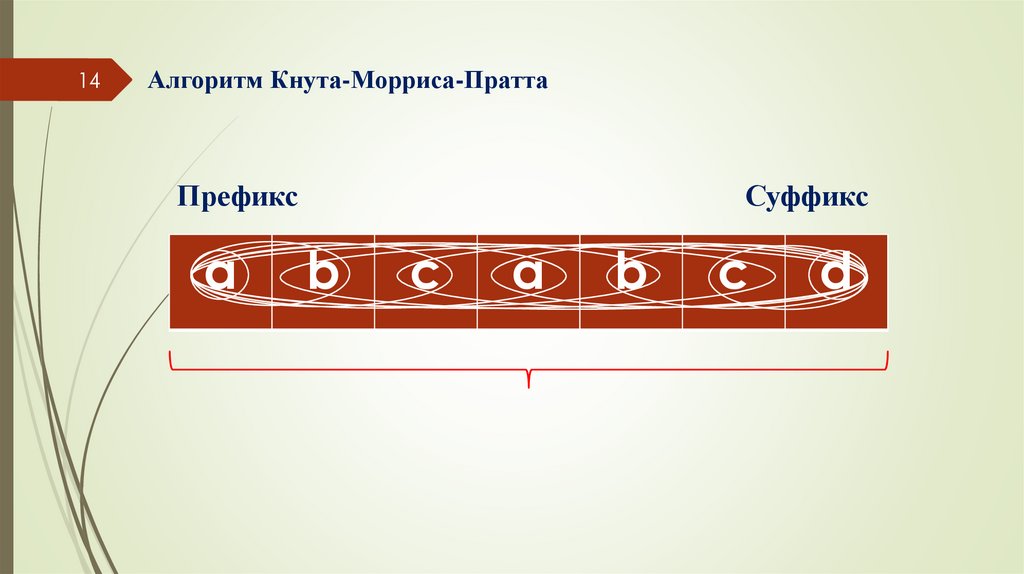
14Алгоритм Кнута-Морриса-Пратта
Префикс
a
Суффикс
b
c
a
b
c
d
15.
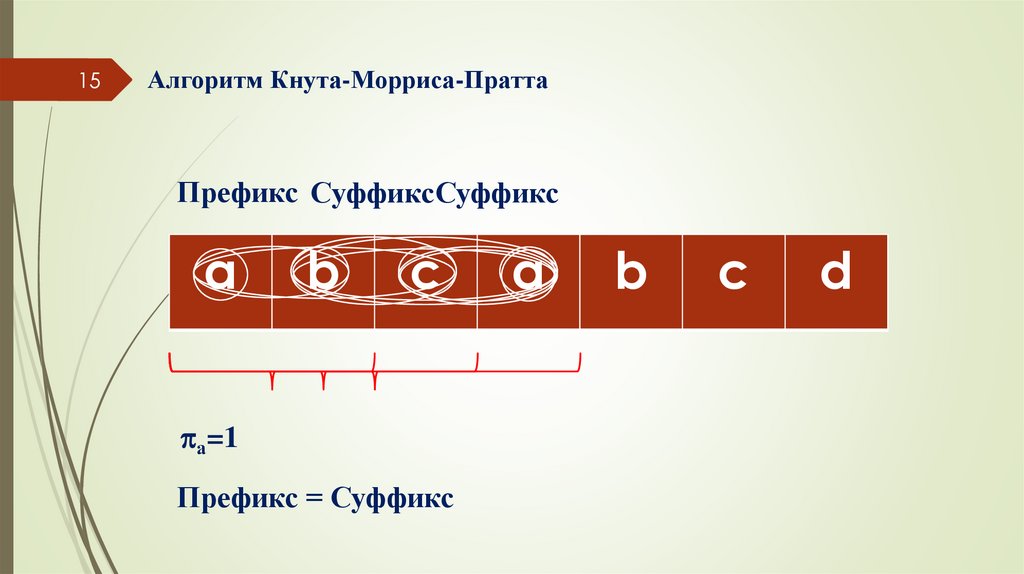
15Алгоритм Кнута-Морриса-Пратта
Префикс СуффиксСуффикс
a
b
c
а=1
Префикс = Суффикс
a
b
c
d
16.
16Алгоритм Кнута-Морриса-Пратта
Префикс-функция для i-го символа образа возвращает
значение, равное максимальной длине совпадающих
префикса и суффикса подстроки в образе, которая
заканчивается i-м символом.
Это значение будем хранить в [i].
17.
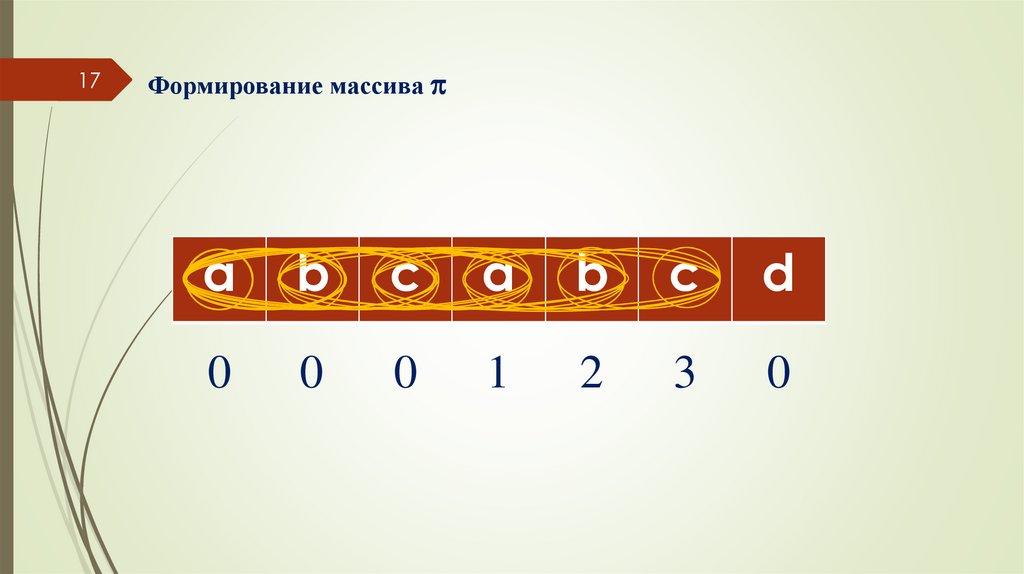
17Формирование массива
a
b
c
a
b
c
d
0
0
0
1
2
3
0
18.
18Формирование массива
a
b
c
a
b
c
a
d
0
0
0
1
2
3
0
4
1
Префикс-функция для i-го символа образа возвращает значение,
равное максимальной длине совпадающих префикса и
суффикса подстроки в образе, которая заканчивается i-м
символом.
19.
19Программная реализация этапа 1
j
ij
ji
ij
ji
i
i
i
0
1
2
3
4
5
6
7
8
а
a
b
b
a
a
b
b
a
b
0
0
0
1
1
2
3
4
2
[0] = 0; i = 1; j = 0;
если аi аj, тогда
тогда, [i]
если= j0;=i0,++;
то [i] = 0; i++;
иначе (т.е. аi = аj) [i]
иначе
= j (т.е.
+ 1; ji ++;
0) jj++
= [j – 1];
20.
20Образ и полученный массив
а
a
b
b
a
a
b
b
a
b
0
0
0
1
1
2
3
4
2
[0] = 0; i = 1; j = 0;
если а
если
(т.е.
аj) [i]
= j j+=1;0,i то
++; [i]
j++= 0; i++;
i аji,=тогда,
(т.е.
= [j – 1];
иначе аi аj, если jиначе
= 0, то
[i]j =0)
0; ji++;
иначе (т.е. аi = аj) [i] = j + 1; i ++; j++
21.
21Этап 1. Псевдокод
[0]=0;
j=0;
i=1;
пока не закончится образ проверяем одно единственное условие:
if аi == аj then [i] = j + 1; i ++; j++;
// аi == аj
else if j == 0, then [i] = 0; i++;
// аi != аj и j == 0
else j = [j – 1];
// аi != аj и j != 0
Сложность кода - О(n), где n это количество символов в образе.
22.
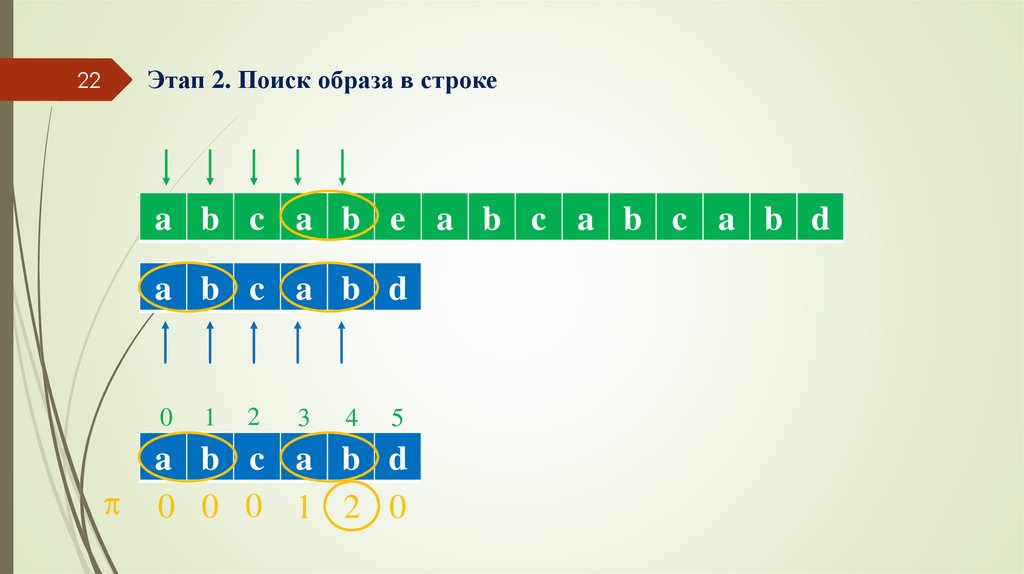
22Этап 2. Поиск образа в строке
a b c a b e a b c a b c a b d
a b c a b d
0
1
2
3
4
5
a b c a b d
0 0 0 1 2 0
23.
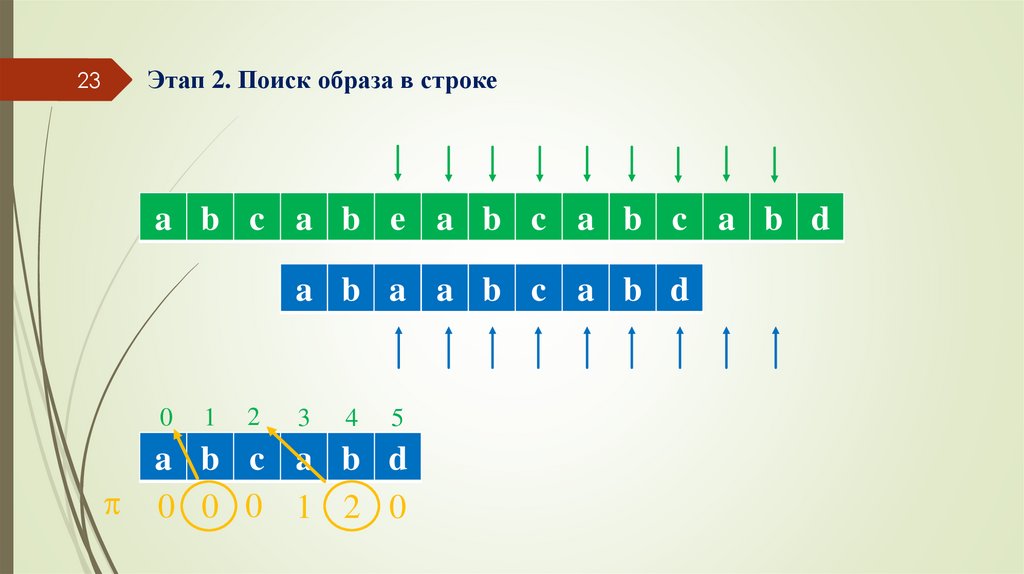
23Этап 2. Поиск образа в строке
a b c a b e a b c a b c a b d
a b ac b
a b
c d
ac b
a d
b d
0
1
2
3
4
5
a b c a b d
0 0 0 1 2 0
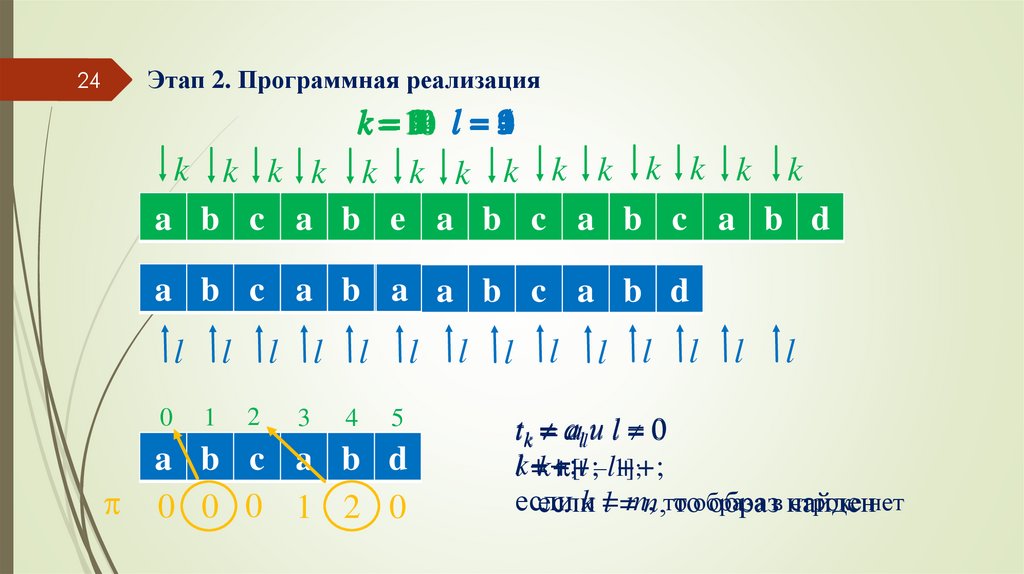
24.
24Этап 2. Программная реализация
13
12
k == 11
9320148765 l = 253410
10
14
k k k k k k k k k k k k k k
a b c a b e a b c a b c a b d
a b c a b dca ab bc dca ab b
d d
l
0
l
l
1
2
l
l
3
4
l
5
a b c a b d
0 0 0 1 2 0
l
l
l
l
l
l
l
l
tk
= ааll и l =
0
k++;
l =k++;
[l –l++;
1];
если
строке нет
еслиk =
l =m,n,тотообраза
образв найден
25.
25Этап 2. Поиск образа в строке
если tk = аl, тогда {k++;
l++;
если l = n, то образ найден}
иначе (т.е. tk аl ),
если l = 0, тогда {k++;
если k = m, то образа в строке нет}
иначе (т.е. l 0) l = [l – 1];
26.
26Этап 2. Псевдокод
k = 0;
l = 0;
пока не закончилась строка проверяем одно
единственное условие:
if tk == аl then k++; l++; if l == n then образ найден
else if l == 0 then k++; if k == m then образа в строке нет
else l = [l – 1];
/* первая строка условия: tk = аl
вторая строка: tk аl и l = 0,
третья строка: tk аl и l 0 */
27.
27Сложность алгоритма Кнута, Морриса, Пратта
Временная сложность алгоритма КМП:
О(n+m)
Временная сложность прямого поиска:
О(n*m)





















 programming
programming








