Similar presentations:
Поиск заданного элемента массива. Лекция 19
1.
Лекция 19.Поиск заданного элемента
массива
2.
План лекции:1. Поиск минимального или максимального
элемента массива
2. Поиск заданного элемента
3. Задачи
3.
Обработка массивовТипичными операциями при работе с массивами
являются:
Организация ввода массива
Ввод с клавиатуры
Заполнение случайными числами (вывод)
Обработка массивов
Поиск min или max элемента массива
Поиск заданного элемента массива
Изменение массива
Сортировка массива
Вывод массива
4.
1. Поиск минимального илимаксимального элемента массива
Алгоритм
нахождения
минимального
(максимального) элемента массива :
сначала дается предположение, что первый
элемент
массива
является
минимальным
(максимальным),
затем
остальные
элементы
массива
последовательно сравниваются с этим элементом.
Если во время очередной проверки обнаружится,
что проверяемый элемент меньше (больше)
минимального (максимального), то этот элемент
становится минимальным (максимальным) и
продолжается проверка оставшихся элементов.
5.
Способы поиск min (max)1 способ: Применяем 2 переменные:
• min - храним значение минимального элемента,
• nmin - номер минимального элемента.
int min=a[0], nmin=0; //считаем a[0] минимальным
for (int i = 1; i < n; i++) //в цикле от 1 до n
{
if (a[i] < min)
//если число меньше минимума
{
min=a[i];
//то запоминаем этот минимум
nmin=i;
//запоминаем номер минимума
}
}
6.
Способы поиск min (max)2 способ: Применяем 1 переменную:
• min - номер минимального элемента
• a[min] – минимальный элемент
int min=0;
//считаем a[0] минимальным
for (int i = 1; i < n; i++) //в цикле от 1 до n
{
if (a[i] < a[min])
//если число меньше минимума
min=i ;
//запоминаем номер минимума
}
7.
Алгоритмпоиска
минимального
элемента
массива
8.
Пример 1.Поиск
минимального
элемента
массива
9.
Пример 2.• Найдите максимальный элемент в массиве,
используя переменную max в качестве номера
максимального элемента.
• Составьте блок-схему поиска максимального
элемента массива.
10.
2. Поиск заданного элемента массиваПри
решении
многих
задач
возникает
необходимость определить, содержит ли массив
определенную информацию или нет.
Например, проверить, есть ли в списке студентов
фамилия Петров, или имеются ли в массиве числа,
кратные 5.
Задачи такого типа называют поиском в массиве.
Для организации поиска в массиве могут быть
использованы различные алгоритмы.
Наиболее простой – это алгоритм простого
перебора.
11.
Алгоритм простого перебораПоиск
осуществляется
последовательным
сравнением элементов массива с образцом до тех
пор, пока не будет найден элемент, равный образцу,
или не будут проверены все элементы.
Алгоритм простого перебора применяется, если
элементы массива не упорядочены.
12.
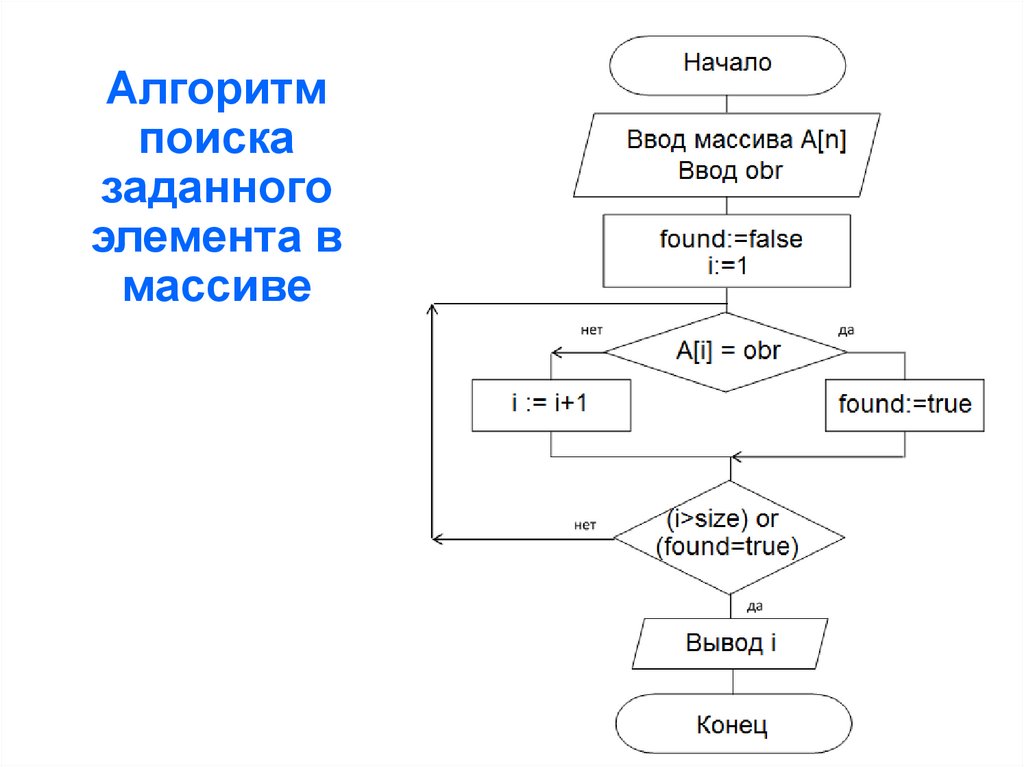
Алгоритм простого перебораОбозначения:
a[n] – исходный массив
obr – число-образец, который нужно искать в массиве,
вводится с клавиатуры
k – номер элемента массива, равного образцу
found – логическая переменная
found=true – образец найден
found=false – образец не найден
13.
Алгоритмпоиска
заданного
элемента в
массиве
14.
Пример 3.Метод простого
перебора (поиск)
15.
Метод бинарного поискаНа практике довольно часто производится поиск
в массиве, элементы которого упорядочены по
некоторому критерию (такие массивы называются
упорядоченными).
Например, массив фамилий, как правило,
упорядочен по алфавиту, массив данных о погоде –
по датам наблюдений.
В случае если массив упорядочен, то применяют
другие, более эффективные по сравнению с методом
простого перебора алгоритмы, один из которых –
метод бинарного поиска.
16.
Метод бинарного поискаДопустим, некоторый массив целых чисел
упорядочен по возрастанию.
Необходимо определить, содержит ли этот массив
некоторое число (образец).
Алгоритм
бинарного
поиска
реализуется
следующим образом:
1. Сначала в массиве определяются
значения:
verh – первый элемент массива,
niz – последний элемент массива,
sred – средний по номеру элемент
массива.
17.
Метод бинарного поиска2. Образец сравнивается со средним по номеру
элементом.
3. Если образец равен среднему элементу, то задача
решена.
4. Если образец больше среднего,
это значит, что искомый элемент
расположен ниже среднего (между
элементами sred+1 и niz),
За новое значение verh
принимается sred+1.
Значение niz не меняется.
18.
Метод бинарного поиска5. Если образец меньше среднего, то это значит, что
искомый элемент расположен выше среднего (между
элементами verh и sred-1),
за новое значение niz
принимается sred-1,
а значение verh не меняется.
19.
Метод бинарного поиска6. После определения части массива, где может
находиться искомый элемент, новое значение sred
вычисляется по формуле:
7. Алгоритм бинарного поиска заканчивается, если
искомый элемент найден или, если перед
выполнением очередного цикла поиска
обнаруживается, что значение verh больше, чем niz.
20.
Алгоритм метода бинарного поиска21.
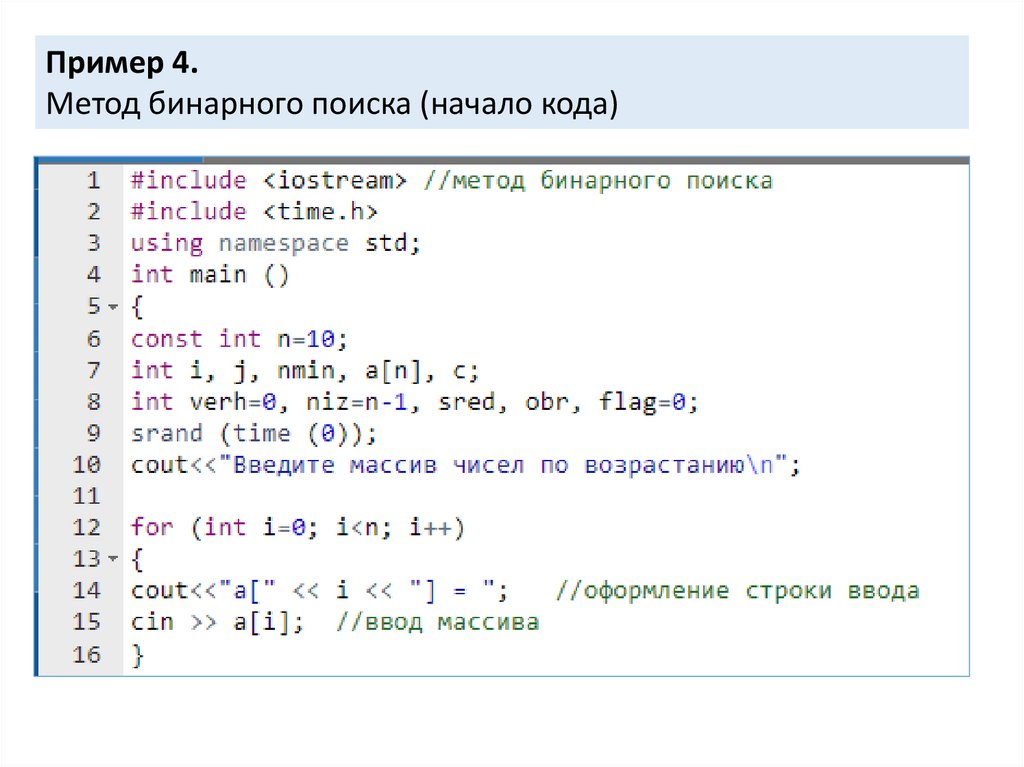
Пример 4.Метод бинарного поиска (начало кода)
22.
Пример 4.Метод бинарного поиска (продолжение кода)
23.
Пример 4.Метод бинарного поиска (выполнение)
24.
Пример 4. Метод бинарного поиска (вывод протокола)Добавьте команду вывода протокола вычисления границ
после команды вычисления sred (после строки 21)
cout<<"verh="<<verh<<" sred="<<sred<<" niz="<<niz<<"\n";
Протокол показывает
количество сравнений
для нахождения
искомого образца
25.
Контрольные задания по теме «Массивы»Задание 1
Цель работы. Задав одномерный массив А целочисленных данных, реализовать
обработку массива, как указано в варианте. Длина массива N<=20. Исходные
данные задать самостоятельно, учитывая формат элементов массива A.
В программе должны быть предусмотрены процедуры ввода-вывода элементов
массива А и его обработки. Исходные данные должны вводиться с проверкой на
область допустимых значений. Тип результата определяется из контекста задачи.



























 programming
programming








