Лекция_3_Топологическая_сортировка

1.

Топологическая
сортировка
Лекция №3 по дисциплине “Методы программирования”

2.

Что такое топология?
Топология (от греч. tоpos — место) — часть геометрии, посвященная
изучению феномена непрерывности (выражающегося, например, в понятии
предела). Разнообразие проявлений непрерывности в математике и широкий
спектр различных подходов к её изучению привели к распадению единой Т.
на ряд отделов («общая Т.», «алгебраическая Т.» и др.), отличающихся друг
от друга по предмету и методу изучения и фактически весьма мало между
собой связанных.

3.

Лента Мёбиуса как объект, изучаемый в топологии

4.

Что такое топология?
Вычислительная топология — раздел, находящийся на пересечении
топологии, вычислительной геометрии и теории вычислительной сложности.
Занимается созданием эффективных алгоритмов для решения
топологических проблем и применением топологических методов для
решения алгоритмических проблем, возникающих в других областях науки.

5.

Топология сетей - примеры построения сети:

6.

Типичный граф зависимостей пакетов программы

7.

Граф зависимостей при установке ПО в Linux

8.

Топологическая сортировка - определение
Топологическая сортировка (Topological sort) — один из основных
алгоритмов на графах, который применяется для решения множества более
сложных задач.
Задача топологической сортировки графа состоит в следующем: указать
такой линейный порядок на его вершинах, чтобы любое ребро вело от
вершины с меньшим номером к вершине с большим номером.
Очевидно, что если в графе есть циклы, то такого порядка не существует.
Ориентированной сетью (или просто сетью) называют бесконтурный
ориентированный граф.
В задачах подобного плана рассматриваются только конечные сети.

9.

Топологическая сортировка - область применения
Топологическая сортировка широко применяется в различных отраслях
например, с её помощью можно построить последовательность прохождения
учебных курсов студентами, последовательность установки программ при
помощи пакетного менеджера, последовательность сборки исходных текстов
программ по данным сборочных файлов, можно построить список
отображения объектов в изометрической проекции зная парные порядковые
отношения между объектами (какой из двух объектов должен быть
прорисован раньше).

10.

От поиска в глубину к топологической сортировке
Поиск в глубину (DFS) идеально подходит для вычисления топологического
упорядочивания (сортировки) ориентированного ациклического графа. Вы
наверняка спросите, что это такое и кого это волнует.
Также стоит заметить, что по правилам русского языка упорядочение - это
приведение в порядок естественным путем, тогда как упорядочивание приведение в порядок в результате внешнего воздействия.
Кроме того, упорядочение является результатом, тогда как
упорядочивание - процессом.

11.

Топологическая сортировка (упорядочивание)
Представьте, что у вас полно задач, которые нужно выполнить, и
существуют ограничения по предшествованию - вы не можете начать
некоторые задачи до тех пор, пока не завершите другие.
Подумайте, например, о курсах вашей университетской программы, которые
необходимы в качестве предварительного условия для других. Одним из
применений топологических упорядочиваний является построение
последовательности операций с целью соблюдения всех ограничений по
предшествованию.

12.

Определение топологической сортировки
Функция f эффективно упорядочивает вершины - от вершины с наименьшим
значением f до вершины с наибольшим значением. Данное условие
утверждает, что все (ориентированные) ребра графа G должны следовать
вперед в упорядочении, при этом метка хвоста ребра должна быть меньше,
чем метка его головы.

13.

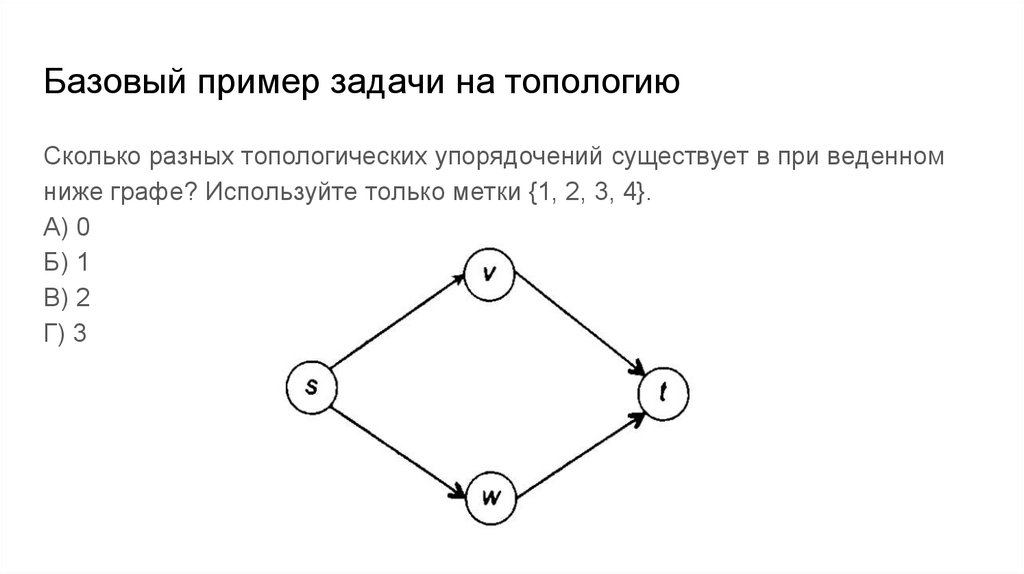
Базовый пример задачи на топологию
Сколько разных топологических упорядочений существует в при веденном
ниже графе? Используйте только метки {1, 2, 3, 4}.
А) 0
Б) 1
В) 2
Г) 3

14.

15.

Решение задачи из базового примера
Вы можете визуализировать топологическое упорядочивание, построив вершины в порядке их значений f.
В топологическом упорядочивании все ребра графа ориентированы слева направо. На рис. 8.1 показаны
топологические упорядочивания, выявленные в решении тестового задания 8.3.
рис. 8.10
Когда вершины графа представляют операции, а ориентированные ребра представляют ограничения по
предшествованию, топологические упорядочивания точно соответствуют разным способам построения
последоваrельности операций при соблюдении ограничений по предшествованию.

16.

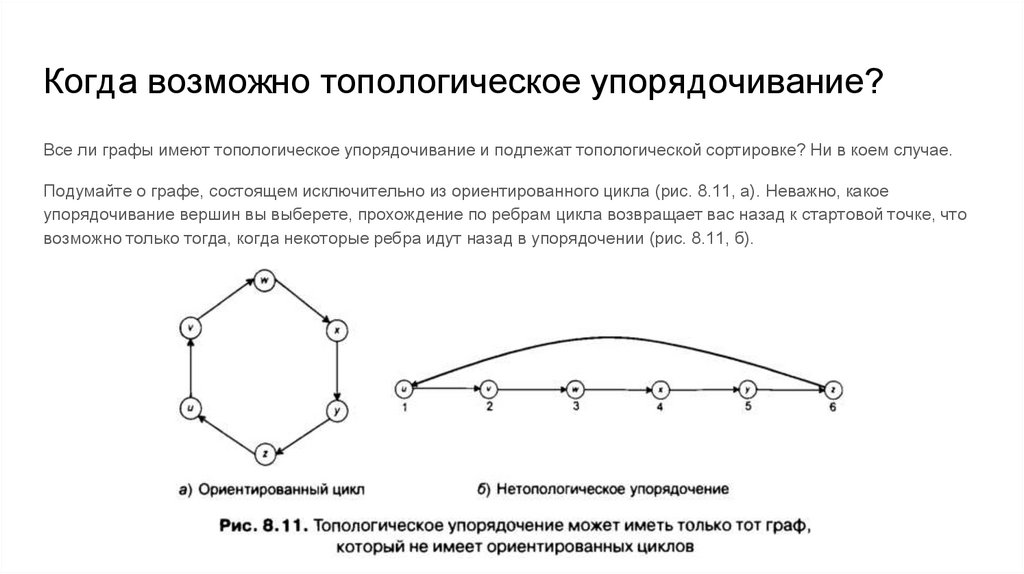
Когда возможно топологическое упорядочивание?
Все ли графы имеют топологическое упорядочивание и подлежат топологической сортировке? Ни в коем случае.
Подумайте о графе, состоящем исключительно из ориентированного цикла (рис. 8.11, а). Неважно, какое
упорядочивание вершин вы выберете, прохождение по ребрам цикла возвращает вас назад к стартовой точке, что
возможно только тогда, когда некоторые ребра идут назад в упорядочении (рис. 8.11, б).

17.

ТЕОРЕМА
Каждый ориентированный
ациклический граф имеет минимум
одно топологическое упорядочение.

18.

Лемма об истоковых вершинах
Для доказательства этой теоремы нам понадобится следующая лемма об
истоковых вершинах.
Истоковая вершина ориентированного графа - это вершина без входящих
ребер. (Схожим образом стоковая вершина - это вершина без исходящих
ребер.) Например, s является единственной истоковой вершиной в графе на
рис. 8.10; ориентированный цикл на рис. 8.11 не имеет истоковых вершин.
Лемма: Каждый ориентированный ациклический граф имеет минимум
одну истоковую вершину.

19.

Лемма об истоковых вершинах
Лемма об истоковых вершинах является истинной, потому что, если вы продолжите
следовать по входящим ребрам назад из произвольной вершины ориентированного ациклического графа, вы обязательно достигнете истоковой вершины. (В противном случае вы
породите цикл, что невозможно.) См. также рис. 8.12

20.

Таким образом… - ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Мы можем доказать исходную теорему, наполняя топологическое
упорядочение слева направо извлекаемыми подряд истоковыми вершинами.
В качестве альтернативы: прослеживание не по входящим, а по исходящим
ребрам в доказательстве леммы об истоковых вершинах показывает, что
граф имеет минимум одну стоковую вершину, и мы можем наполнить
топологическое упорядочение справа налево извлеченными подряд
стоковыми вершинами.

21.

Таким образом… ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Пусть G равно ориентированному ациклическому графу с n вершинами.
План состоит в присвоении вершинам значений f в порядке возрастания от 1
до n.
Какая вершина заслужила право иметь единицу в качестве своего значения
f? Хорошо бы, чтобы это была истоковая вершина - если вершине с
входящим ребром была присвоена первая позиция, то входящее ребро
будет предыдущим в упорядочении.
Таким образом, пусть v1, равно истоковой вершине графа G - одна такая
существует по лемме об истоковых вершинах - и назначим f(v1) = 1. Если
существует несколько истоковых вершин, то выберем одну из них
произвольно.

22.

Таким образом… ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Далее, мы получим граф G' из G, удалив вершину v1, и все ее ребра. Поскольку G является ориентированным ациклическим графом, то таковым
является и G' - удаление элементов не может создать новые циклы.
Поэтому мы можем рекурсивно вычислить топологическое упорядочение
графа G', используя метки {2, 3, 4, …, n}, причем каждое ребро в G' следует
в упорядочении вперед. (Поскольку каждый рекурсивный вызов выполняется
на меньшем графе, рекурсия в конечном итоге остановится.)
Только те ребра в G, которые одновременно не находятся в G', являются
(исходящими) ре брами вершины v1; поскольку f(v1) = 1, они также следуют
в упорядочении вперед. Ч. т. д.

23.

Выводы после доказательства теоремы
Доказательства леммы об истоковых вершинах и теоремы, описанной ранее, естественным
образом приводят к алгоритму:
Для n-вершинного ориентированного ациклического графа, представленного в виде списков
смежности, первое доказательство дает О(n) временную подпрограмму для нахождения
истоковой вершины.
Последнее доказательство вычисляет топологическое упорядочивание с n вызовами этой
подпрограммы, выхватывая новую истоковую вершину на каждой итерации.
Время работы этого алгоритма составляет О(n2), то есть линейно-временное для самых
плотных графов, но не для более разреженных графов. Так же имеется более оптимальное
решение посредством поиска в глубину, приводящее к линейно временному (О(m + n))
алгоритму.

24.

Топологическая сортировка узлов
ациклического ориентированного
графа
(практическая часть)

25.

Напоминание о применимости:
Топологическая сортировка применима и к произвольным ациклическим
ориентированным графам (двоичное дерево – частный случай такого графа).
Ациклический граф можно использовать для графического изображения
частично упорядоченного множества (когда в множестве есть отношение
порядка, но не для всех элементов: некоторые элементы несравнимы).
Цель топологической сортировки - преобразовать частичный порядок в
линейный. Графически это означает, что все узлы графа нужно расположить
на одной прямой таким образом, чтобы все дуги графа, соединяющие его
узлы, были направлены в одну сторону.

26.

Пример из математики
Пусть частичный порядок задается следующим набором отношений между
ключами:
a < b, b < d, d < f, b < l, d < h, f < c, a < c,
c < e, e < h, g < e, g < k, k < d, k < l

27.

Этот набор отношений можно представить в виде ациклического графа
(рисунок 6), причем каждое отношение представляет дугу указанного графа

28.

Задача состоит в том, чтобы привести граф с рисунка 6 к линейному графу,
показанному на рисунке 7.
Ключи после топологической сортировки будут расположены, например, в следующем
порядке: g k a b d f c e h l (понятно, что топологическая сортировка неоднозначна, так
что это один из возможных топологических порядков).
Последовательная обработка полученного линейного списка узлов графа
эквивалентна их обработке в порядке обхода графа.

29.

Описание алгоритма. Структуры данных.
Находим узел x графа, у которого нет предшествующих узлов (по крайней мере один
такой элемент должен существовать, так как иначе у графа были бы циклы). Этот
узел, будем называть его «ведущим» узлом, поместим в начало линейного списка
узлов и удалим из графа. Поскольку оставшийся граф останется ациклическим, можно
применять описанное преобразование до тех пор, пока все узлы графа не станут
«ведущими» и перейдут в линейный список.

30.

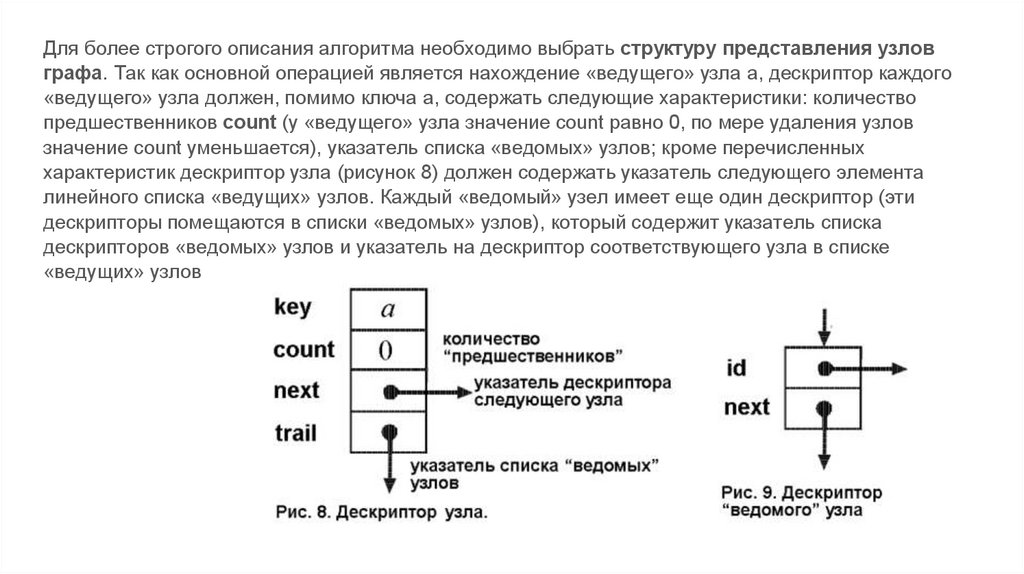
Для более строгого описания алгоритма необходимо выбрать структуру представления узлов
графа. Так как основной операцией является нахождение «ведущего» узла a, дескриптор каждого
«ведущего» узла должен, помимо ключа a, содержать следующие характеристики: количество
предшественников count (у «ведущего» узла значение count равно 0, по мере удаления узлов
значение count уменьшается), указатель списка «ведомых» узлов; кроме перечисленных
характеристик дескриптор узла (рисунок 8) должен содержать указатель следующего элемента
линейного списка «ведущих» узлов. Каждый «ведомый» узел имеет еще один дескриптор (эти
дескрипторы помещаются в списки «ведомых» узлов), который содержит указатель списка
дескрипторов «ведомых» узлов и указатель на дескриптор соответствующего узла в списке
«ведущих» узлов

31.

Описание алгоритма. Фаза ввода.
Пусть исходные данные представлены в виде множества пар ключей (*). Пары
ключей вводятся в произвольном порядке. После ввода очередной пары x < y ключи
ищутся в списке «ведущих» (например, с помощью функции find) и в случае
отсутствия добавляются к нему. Затем в список «ведомых» для x добавляется
дескриптор y и счетчик предшественников y увеличивается на 1 (сначала значения
всех счетчиков равны 0).

32.

По окончании фазы ввода будет сформирована структура, показанная на рисунке 10.

33.

Описание алгоритма. Фаза сортировки.
На фазе сортировки строим цепочку дескрипторов, у которых счетчик имеет значение
0, одновременно корректируя счетчики «ведомых» узлов.
Так как с каждой такой коррекцией значение счетчика уменьшается на 1, постепенно
значения всех счетчиков становятся равными 0, и соответствующие узлы включаются
в результирующую цепочку.

34.

Описание программного кода топологической сортировки.
Дескриптор ведущего узла графа:

35.

Описание программного кода топологической сортировки.
Дескриптор ведомого узла графа:
Счетчик ведущих узлов:
Два вспомогательных узла:

36.

Описание программного кода топологической сортировки.
Функция поиска по ключу: