函数与极限
1.
第一章第四节
函数与极限
无穷小量与无穷大量(2课时)
• 无穷小量及其阶的概念
• 无穷小的等价代换
• 无穷大量
• 小结与思考题
2.
第一部分无穷小量及其阶的概念
一、无穷小量
如果 lim f ( x) 0 (或 lim
x x0
x
f ( x) 0)
则称函数 f ( x ) 当 x x 0 (或 x ) 时为无穷小
注意
2.零是可以作为无穷小的唯一的数.
3.
例如,lim sin x 0, 函数 sin x是当x 0时的无穷小.
x 0
1
lim 0,
x x
1
函数 是当x 时的无穷小.
x
( 1) n
( 1) n
lim
0, 数列{
}是当n 时的无穷小.
n
n
n
lim ln(1 x) 0
x 0
lim(e 1) 0
x
x 0
4.
2.无穷小与函数极限的关系:定理 1
lim f ( x ) A f ( x ) A ( x ),
x x0
其中 ( x )是当 x x 0 时的无穷小.
f ( x ) A, 令 ( x ) f ( x ) A,
证 必要性 设 xlim
x
0
则有 lim ( x ) 0,
x x0
f ( x ) A ( x ).
充分性 设 f ( x ) A ( x ),
其中 ( x )是当x x 0时的无穷小,
则 lim f ( x ) lim ( A ( x )) A lim ( x ) A.
x x0
x x0
x x0
5.
3.无穷小的运算性质:定理2 在同一过程中,有限个无穷小的代数
和仍是无穷小.
证 设 x 及 x 是当x 时的两个无穷小, 则
lim[ x x ] 0
x
同理,有限个无穷小的代数和仍是无穷小.
6.
定理3有界函数与无穷小的乘积是无穷小.
证 设函数u x 在U 0 ( x0 , 1 )内有界
则 M 0, 1 0, 使得当0 x x0 1时
恒有 u x M .
又设 x 是当x x0时的无穷小,
0, 2 0, 使得当0 x x0 2时
恒有 x
M
.
7.
取 min{ 1 , 2 }, 则当 0 x x0 时, 恒有u x x u x x M
,
M
当x x0时, u x x 为无穷小.
推论1
常数与无穷小的乘积是无穷小.
推论2
有限个无穷小的乘积也是无穷小.
1 2
1
例如,当x 0时, x sin , x arctan 都是无穷小
x
x
x sin x, x 2 都是无穷小.
8.
二、无穷小量阶的概念1
例如, 当x 0时, x , x , sin x , x sin 都是无穷小.
x
2
x
2
lim
0
,
x
比x要快得多;
x 0 x
观
察
sin x
sin x与x大致相同 ;
1,
各 lim
x 0
x
极
1
2
x sin
限
x lim sin 1
lim
不存在. 不可比.
2
x 0
x
0
x
x
2
极限不同,
不同.
2
反映了趋向于零的“快慢”程度
9.
定义:设 x , x 是同一过程中的两个无穷小, 且 x 0.
x
(1) 如果 lim
0, 就说 x 是比 x 高阶的无穷小,
x
记作 x o( x );
x
( 2) 如果 lim
C 0, 就说 x 与 x 是同阶的无穷小;
x
x
特殊地 如果 lim
1, 则称 x 与 x 是等价的无穷小;
x
记作 x ~ x ;
x
(3) 如果 lim
C 0, k 0), 就说 x 是 x 的k阶的
k
x
无穷小.
10.
例1 证明 : 当x 0时,4 x tan 3 x为x的四阶无穷小.4 x tan 3 x
tan x 3
4 lim (
) 4,
解 lim
4
x 0
x 0
x
x
故当x 0时,4 x tan 3 x为x的四阶无穷小.
例2 当x 0时, 求 tan x sin x关于x的阶数.
tan x sin x
tan x 1 cos x
1
lim (
) ,
解 lim
3
2
x 0
x 0
x
x
x
2
tan x sin x为x的三阶无穷小.
11.
例证明下列关系式
x
(2) 1 x 1 o( x)
(1) arctan x x o( x)
n
3
x
(3) 1 tan x 1 sin x ~
4
arctan x x x 0
(1)
0
证
x
x
n
1 x 1
x 0
n
(2)
0
x
n
1 tan x 1 sin x x 0
(3)
1
3
x
4
12.
当x 0时,常用等价无穷小:
sin x ~ x ,
tan x ~ x ,
ln(1 x ) ~ x ,
arcsin x ~ x ,
arctan x ~ x ,
e 1 ~ x,
x
n
1
1 x 1 ~ x
n
1 2
1 cos x ~ x .
2
用等价无穷小可给出函数的近似表达式:
x
lim
1, lim x x 0,
x
x
即 x x o( x ), 于是有 x x o( x ).
1 2
2
sin
x
x
o
(
x
),
cos
x
1
x
o
(
x
).
例如,
2
13.
第二部分无穷小的等价代换
定理(等价无穷小代换定理)设
x ~ x , x ~ x
x
x
lim
.
lim
x
x
x
x x x
lim(
)
证: lim
x
x x x
x
x
x
x
lim
lim
lim
lim
.
x
x
x
x
14.
2tan 2 x
例3 求 lim
.
x 0
1 cos x
1 2
解 当x 0时, 1 cos x ~ x , tan 2 x ~ 2 x .
2
2
(2 x )
原式 lim
8.
x 0 1
x2
2
注意 不能滥用等价无穷小代换.
对于代数和中各无穷小不能分别替换.
15.
tan x sin x.
例4 求 lim
3
x 0
sin 2 x
错 解 当x 0时, tan x ~ x , sin x ~ x .
x x
原式 lim
3 0.
x 0
(2 x )
解
当x 0时, sin 2 x ~ 2 x ,
1 3
tan x sin x tan x(1 cos x ) ~ x ,
2
1 3
x
1
2
.
原式 lim
3
x 0
( 2 x ) 16
16.
例5tan 5 x cos x 1
求 lim
.
x 0
sin 3 x
解 tan 5 x 5 x o( x), sin 3 x 3 x o( x ),
1 2
1 cos x x o( x 2 ).
2
1 2
5 x o( x ) x o( x 2 )
2
原式 lim
x 0
3 x o( x )
o( x ) 1
o( x 2 )
5
x
5
x
2
x
.
lim
x 0
o( x )
3
3
x
17.
3例6
求 lim
解
x 0
lim
x 0
3
2
1 tan x 1 1 x 1
.
tan x sin x
1 tan x 1
tan x sin x
2
tan x x
3 2
= lim
x 0
tan x sin x
1
tan x x 2
lim
6 x 0 tan x (1 cos x)
1
3
1 x2 1
18.
例证明下列关系式
(1) arctan x x o( x), ( x 0)
证
(2) x x 2 tan x ~ x, ( x 0)
x
n
(3) 1 x 1 o( x), ( x 0)
n
arctan x x
arctan x x
lim(
) 0
(1) lim
x 0
x 0
x
x
x
2
2
x
x
tan x 1
x x tan x
lim(
)
(2) lim
x 0 x
x 0
x
x
x
n
1 x 1
n
1 x 1 1
n
(3) lim
lim(
) 0
x 0
x
0
x
x
n
18
19.
第三部分无穷大量
一、无穷大量
如果对于任意给定的正数 M (不论它多么大),
总存在正数 (或正数 X ),使得当 0 x x0
(或 x X
)时
有
f ( x) M
则称 x x 0 (或
简称无穷大。
记作
x )时, f ( x ) 为无穷大量
lim f ( x ) (或 lim f ( x ) ).
x x0
x
20.
特殊情形 正无穷大 负无穷大lim f ( x ) (或 lim f ( x ) )
x x0
( x )
x x0
( x )
注意 1.无穷大是变量,不能与很大的数混淆;
2.切勿将 lim f ( x ) 认为极限存在.
x x0
3. 无穷大是一种特殊的无界变量,但是
无界变量未必是无穷大.
21.
11
例如, 当x 0时, y sin
x
x
是一个无界变量, 但不是无穷大.
(1) 取 x 0
1
( k 0,1,2,3, )
2k
2
y ( x 0 ) 2 k ,
当k充分大时, y( x 0 ) M .
2
1
( 2) 取 x 0
( k 0,1,2,3, )
2k
无界
当k充分大时, x k ,
但 y( x k ) 2k sin 2k 0 M .
不是无穷大
22.
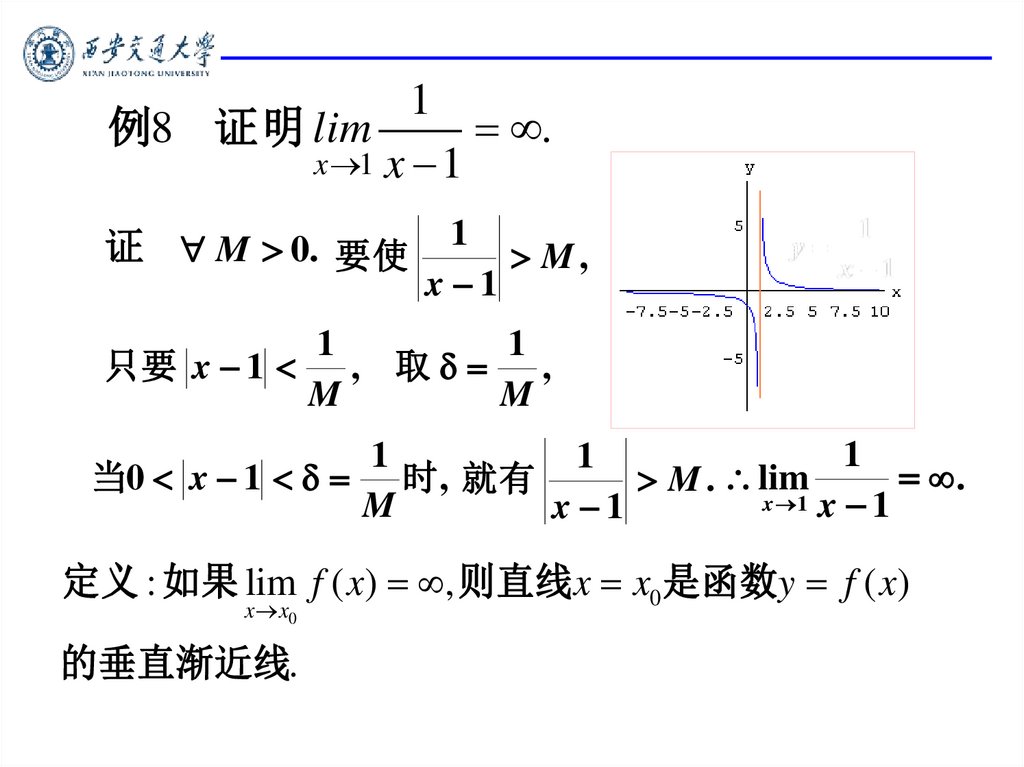
1例8 证明 lim
.
x 1 x 1
证 M 0. 要使
1
M,
x 1
1
1
只要 x 1
, 取
,
M
M
1
1
1
.
当0 x 1 时, 就有
M . lim
x 1 x 1
M
x 1
定义 : 如果 lim f ( x) , 则直线x x0是函数y f ( x)
x x0
的垂直渐近线.
23.
2 x 2 3x 4例 (1) lim
x 3
x 3
2n 2 3n 4
(2) lim
n
n 3
2 x 2 3x 4
(3) lim
x
x 3
(4) lim 2n
n
1
x
(5) lim e
x 0
1
(6) lim ln
x 0
x
24.
二、无穷小与无穷大的关系定理4 在同一过程中,无穷大的倒数为无穷小;
恒不为零的无穷小的倒数为无穷大.
证
设 lim f ( x ) .
x x0
0, 0, 使得当0 x x 0 时
1
1
恒有 f ( x ) , 即
.
f ( x)
1
当x x 0时,
为无穷小.
f ( x)
25.
反之, 设 lim f ( x ) 0, 且 f ( x ) 0.x x0
M 0, 0, 使得当0 x x 0 时
1
恒有 f ( x )
,
M
1
由于 f ( x ) 0, 从而
M.
f ( x)
1
当x x 0时,
为无穷大.
f ( x)
意义 关于无穷大的讨论,都可归结为关于无穷
小的讨论.
26.
例证
1 22 32
lim 3 3 3
n n
n n
n2
3
n
1 22 32
n2
lim 3 3 3 3
n n
n n
n
1
22
32
n2
lim 3 lim 3 lim 3 0
lim
3
n n
n n n n n n
?
1 22 32
n2
lim 3 3 3 3
n n
n n
n
1
lim 3 12 22 32 42 n 2
n n
1 n(n 1)(2n 1) 1
lim 3
3
n n
6
无穷个无穷小的和
不一定是无穷小
27.
第四部分小结
1.无穷小概念及其阶的比较:
反映了同一过程中, 两无穷小趋于零的速度快慢,
但并不是所有的无穷小都可进行比较.
高(低)阶无穷小;
等价无穷小;
无穷小的阶.
2.等价无穷小的替换:
求极限的又一种方法,
注意适用条件.
3.无穷小与无穷大是相对于过程而言的.
(1)无穷小 大 是变量,不能与很小 大
淆 零是唯一的无穷小的数
的数混
(2)无穷多个无穷小的代数和 乘积 未必是无穷小.
(3)无界变量未必是无穷大.
28.
思考题若 f ( x ) 0 且 lim f ( x ) A
x
问 能否保证有 A 0的结论 试举例说明.
答 不能保证.
1
例 f ( x)
x
x 0,
1
lim f ( x ) lim A 0.
x x
x
1
有 f ( x) 0
x



























 mathematics
mathematics