Similar presentations:
Основы математической логики
1.
Основыматематической
логики
2.
Логика — это наука, которая занимаетсяисследованием способов, методов
рассуждения.
3.
ВысказыванияВысказывание (суждение) в логике — это
всегда повествовательное предложение, про
содержание которого важно сказать лишь,
истинное оно или ложное.
Например,
высказывание { Москва — столица России } истинно, а
высказывание { Все углы треугольника — прямые } — ложно.
Такие высказывания называются простыми.
4.
Обозначение высказыванийA { Москва — столица России }
B { Все углы треугольника — прямые }
Логические переменные A и B
значения: «истина» или «ложь».
могут
принимать
«Истина» обозначается символом И или 1 (единица), а
«ложь» — символом Л или 0 (ноль).
5.
Из простых высказываний при помощиспециальных логических связок: «и», «или»,
«не», «если …, то …», «эквивалентно» —
могут
быть
образованы
сложные
высказывания. Например:
«Носорог — это птица» или «Вода
бесцветная»,
Если «Путин – президент США», то
«Москва – столица Египта».
Если «Идет дождь», то «Асфальт - мокрый».
6.
Логические операции1. Инверсия
(от лат. inversio — переворачиваю)
Это логическое отрицание образуется
при помощи частицы «не».
Обозначается символом или чертой сверху .
Например: А или А.
Читается: «инверсия А», «отрицание А» или «не
А».
7.
Таблица истинности дляинверсии
A
A
0
1
1
0
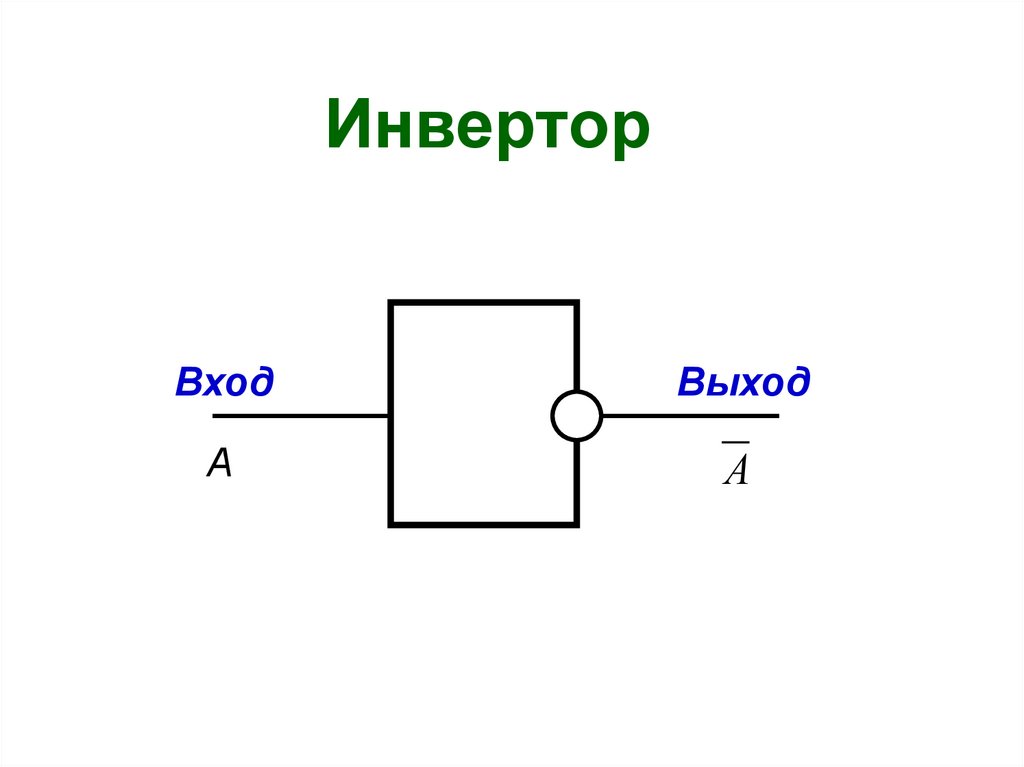
8.
ИнверторВход
Выход
А
А
9.
2. Конъюнкция(от лат. conjunctio — связываю)
Конъюнкция или логическое умножение
образуется при помощи связки «и».
Обозначается символом * или & или .
Например: А * B или A & B или А B .
Читается: «А и B».
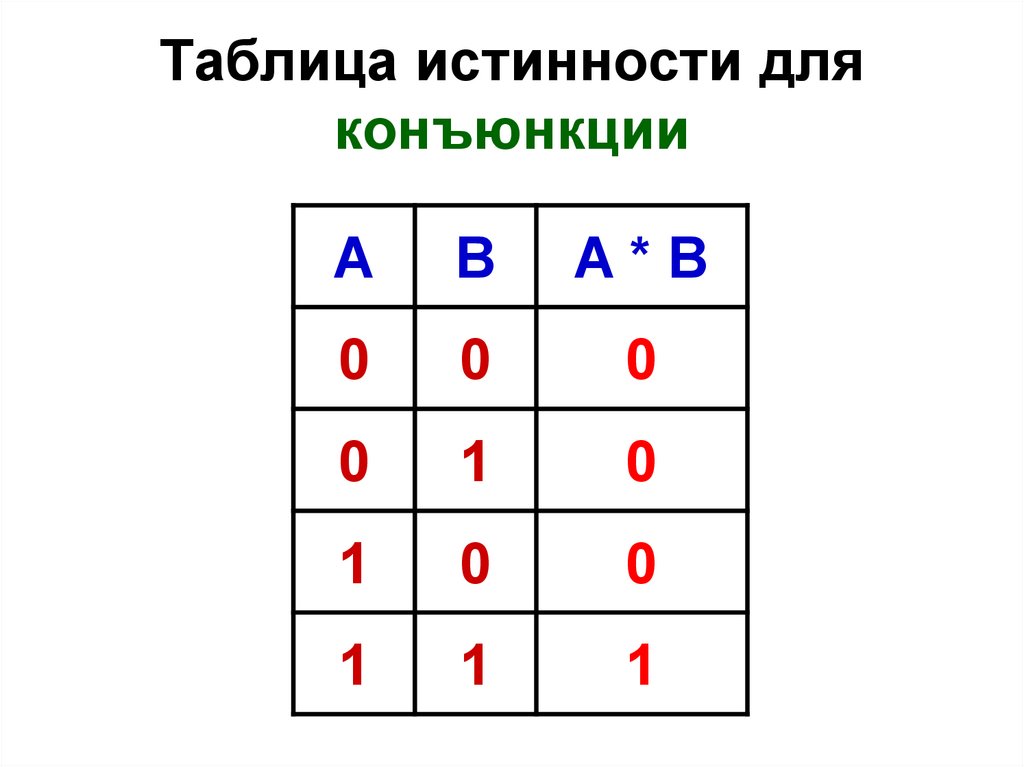
10.
Таблица истинности дляконъюнкции
A
B
A*B
0
0
0
0
1
0
1
0
0
1
1
1
11.
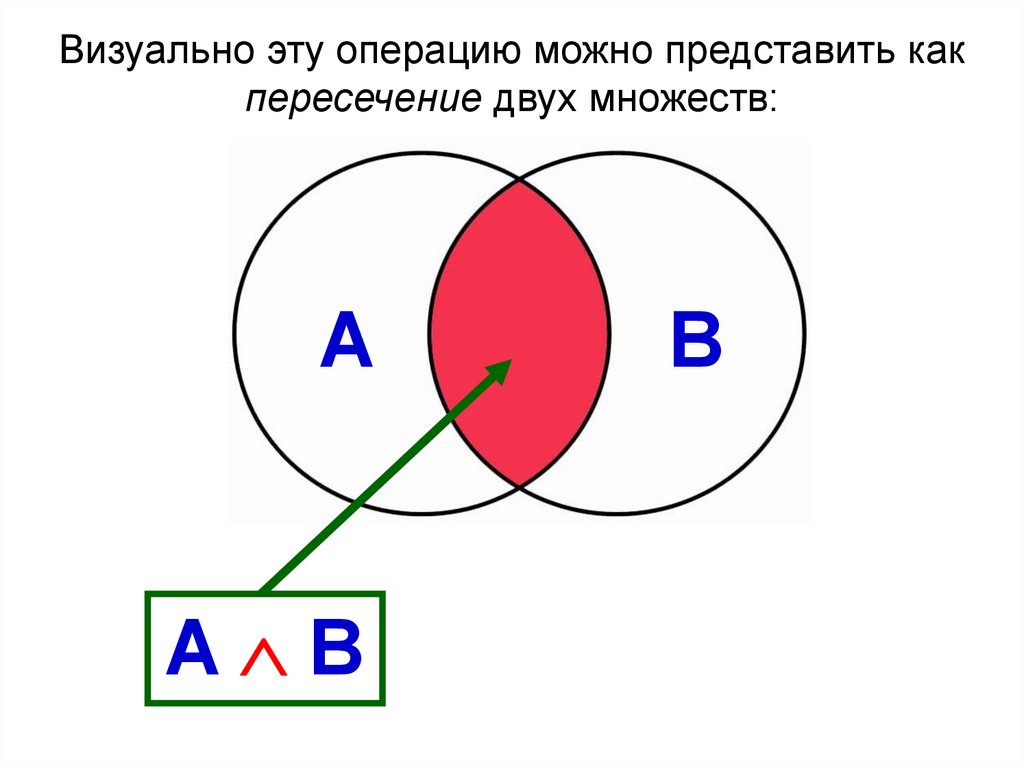
Визуально эту операцию можно представить какпересечение двух множеств:
A
A B
B
12.
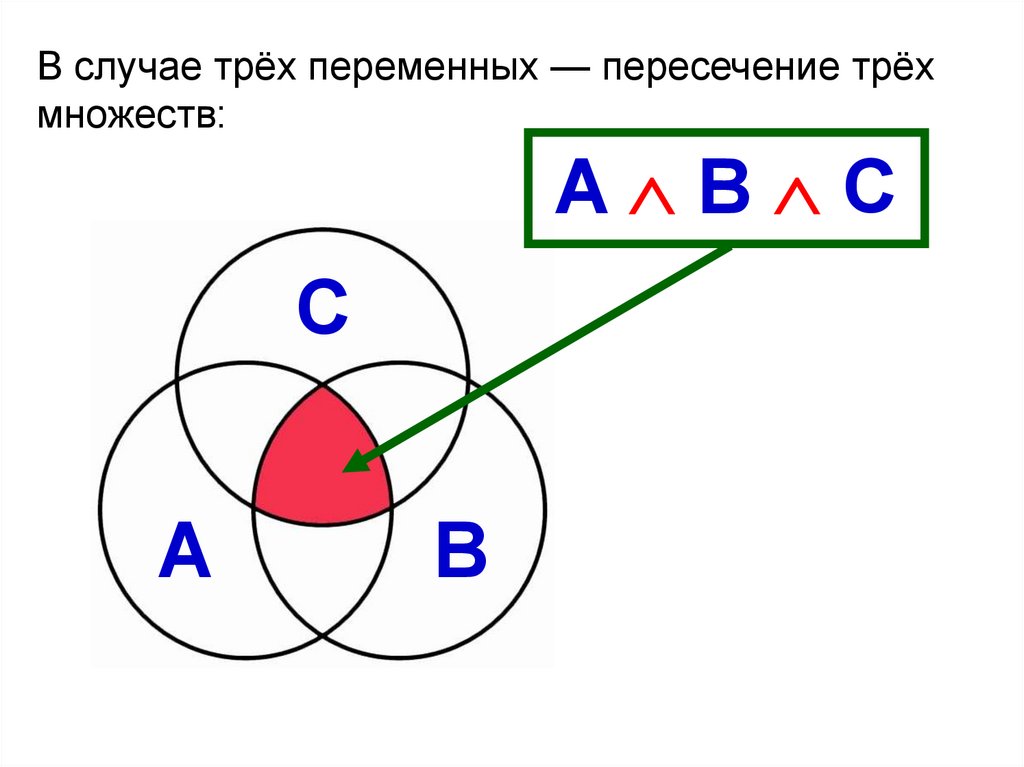
В случае трёх переменных — пересечение трёхмножеств:
A B C
C
A
B
13.
Если в операции участвуют трипеременные,
то
таблица
истинности будет такой:
№
набора
A B C A B C
0
0
0
0
0
1
0
0
1
0
2
0
1
0
0
3
0
1
1
0
4
1
0
0
0
5
1
0
1
0
6
1
1
0
0
7
1
1
1
1
14.
Элемент «2-И-НЕ»«2-И»
Вход 1
&
Выход
Вход 2
15.
3. Дизъюнкция(от лат. disjunctio — различаю)
Дизъюнкция или логическое сложение
образуется при помощи связки «или».
Обозначается символом + или или | .
Например: А + B или А B или A | B.
Читается: «А или B».
16.
Таблица истинности длядизъюнкции
A
B
A B
0
0
0
0
1
1
1
0
1
1
1
1
17.
Визуально эту операцию можно представить какобъединение двух или нескольких множеств:
A
B
A B
18.
Элемент «2-ИЛИ-НЕ»«2-ИЛИ»
Вход 1
1
Выход
Вход 2
19.
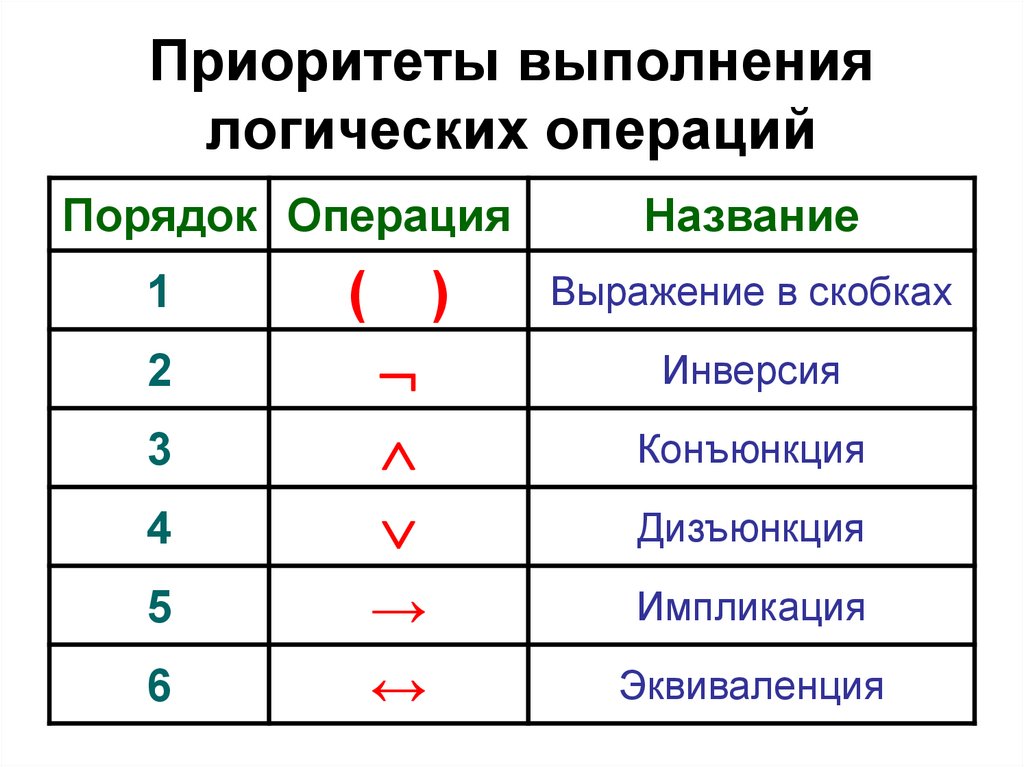
Приоритеты выполнениялогических операций
Порядок Операция
1
2
3
4
5
6
(
)
→
↔
Название
Выражение в скобках
Инверсия
Конъюнкция
Дизъюнкция
Импликация
Эквиваленция
20.
Законы алгебры логикиЗаконы коммутативности
(переместительные)
A B = B A
A B = B A
21.
Законы алгебры логикиЗаконы ассоциативности
(сочетательные)
(A B) С = A (B C)
(A B) С = A (B C)
22.
Законы алгебры логикиЗаконы дистрибутивности
(распределительные)
(A B) (A С) = A (B C)
(A B) (A С) = A (B C)
23.
Законы алгебры логикиЗаконы поглощения
A (A C) = A
A (A C) = A
24.
Законы алгебры логикиЗаконы склеивания
(A С) (A C) = A
(A С) (A C) = A
25.
Законы алгебры логикиЗаконы идемпотентности
A A = A
A A = A
26.
Законы алгебры логикиЗаконы де Моргана
(общей инверсии)
(A B) = A B
(A B) = A B
27.
Закон непротиворечияA A = 0
Закон исключённого третьего
A A = 1
Закон двойного отрицания
( A) = A
28.
Законы исключения константA 0 = A
A 0 = 0
A 1 = 1
A 1 = A
29.
Закон контрапозиции(перевёртывания)
A → B = B → A
Формулы снятия импликации
и эквиваленции
A → B = A B
A ↔ B = (A B) ( A B)
30.
ПримерыПостроить таблицы истинности
и упростить логические выражения:
1.
(А и В) или (не А и В);
2.
А или (А и В);
3.
(А или В) и (не А или В);
4.
А или (не А);
5.
А и (не А).
31.
ПримерыУпростить логические выражения:
1. (А и (не В)) или ((не А) и В) и(А или В);
2. (не(А или В)) и (не(А и ((не В) или (не А))));
3. (не А и В) или (А и В и (А или (не В)).
4. не(А и В) и не(А или не(не В или А));
5. не(не А или В) или не(А или не(не В и не А)).
32.
Решение задач. СамостоятельноУпростите выражения:
1. (A B) ( A B) (A B)
2. ( A B) (A B (A B))
3. ( A B) (A (B A))
4. (A B) ( A ( B A))
5 . (A B) (A ( B A))
6. (А В) ((А В) ( А В))
33.
Решение задач. ОтветыУпростите выражения:
1. (A B) ( A B) (A B)
Ответ.(A* B+ A*B)
2. ( A B) (A B (A B))
Ответ.( B)
3. ( A B) (A (B A))
Ответ. (0)
4. (A B) ( A ( B A))
Ответ. (0)
5 . (A B) (A ( B A))
Ответ.( А* В)
6. (А В) ((А В) ( А В))
Ответ.(А* В+ А*В)
34.
Примеры1. Доказать правильность второго закона
склеивания с помощью преобразования
логического высказывания:
(A С) (A C) = A
2. Доказать законы де Моргана с помощью
построения таблиц истинности.
3. Построить логическую схему для выражений:
(A С) (A C)
(A В) ( A В)
35.
Решение задач. Самостоятельно1. Доказать правильность первого закона
склеивания с помощью преобразования
логического высказывания:
(A С) (A C) = A
2. Доказать законы дистрибутивности с помощью
построения таблиц истинности.
(A B) (A С) = A (B C)
(A B) (A С) = A (B C)
3. Построить логическую схему для выражения:
(A С) ( A C)






























 informatics
informatics