Similar presentations:
Системы счисления
1. Системы счисления
1. Введение2. Двоичная система
3. Восьмеричная система
4. Шестнадцатеричная система
2. Системы счисления
Тема 1. Введение3.
ОпределенияСистема счисления – это совокупность правил для
обозначения и наименования чисел.
Числа:
123, 45678, 1010011, CXL
Цифры:
0, 1, 2, …
I, V, X, L, …
Алфавит – это набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Типы систем счисления:
непозиционные –системы счисления, в
которой количественный эквивалент каждой
цифры не зависит от ее положения (места,
позиции) в записи числа;
3
4.
Определенияпозиционные – система счисления, в
которой значение цифры зависит от ее места
(позиции) в записи числа.
Основание системы счисления ( q )– это
количество знаков или символов, используемых
для изображения числа в данной системе
счисления.
4
5.
Непозиционные системыУнарная – для записи любых чисел используется всего
один символ- палочка, узелок, камушек.
5
6.
Непозиционные системыОбозначение чисел и счёт в Древнем Египте
Ключевые числа 1, 10, 100 и т.д. обозначались
специальными значками – иероглифами.
Например, число 5736
записывалось следующим
образом:
6
7.
Непозиционные системыЯсачные грамоты.
Ясак – уплата подати.
Употребляемые знаки
означают:
Например, 1232 рубля
24 копейки
изображались так:
7
8.
Славянская система счисленияалфавитная система счисления (непозиционная)
8
9.
Римская система счисленияПравила:
(обычно) не ставят больше трех одинаковых цифр
подряд
если младшая цифра (только одна!) стоит слева от
старшей, она вычитается из суммы (частично
непозиционная!)
Примеры:
MDCXLIV = 1000 + 500 + 100 – 10 + 50 – 1 + 5 = 1644
2389 = 2000 + 300 +
MM
CCC
80
LXXX
+
9
IX
2389 = M M C C C L X X X I X
9
10.
Примеры:999 = CMXCIX
2986 = MMCMLXXXVI
CDXLIV = 444
LXXXVI = 86
10
11.
Римская система счисленияНедостатки:
для записи больших чисел (>3999) надо вводить
новые знаки-цифры (V, X, L, C, D, M)
как записать дробные числа?
как выполнять арифметические действия:
CCCLIX + CLXXIV =?
Где используется:
номера глав в книгах:
обозначение веков: «Пираты XX века»
циферблат часов
11
12.
Позиционные системыПозиционная система: значение цифры определяется
ее позицией в записи числа.
Десятичная система:
первоначально – счет на пальцах
изобретена в Индии, заимствована арабами, завезена в Европу
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание (количество цифр): 10
сотни десятки единицы
2
1
0
3 7 8
300 70
разряды
= 3·102 + 7·101 +
8·100
8
Другие позиционные системы:
• двоичная, восьмеричная, шестнадцатеричная (информатика)
• двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов)
• двадцатеричная (1 франк = 20 су)
12
• шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)
13. Системы счисления
Тема 2. Двоичная системасчисления
14.
Перевод целых чиселДвоичная система:
Алфавит: 0, 1
Основание (количество цифр): 2
10 2
19
18
1
2
9
8
1
2
4
4
0
2
2
2
2
1
система
счисления
0
2 10
43210
19 = 100112
разряды
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
14
15.
Примеры:131 =100000112
79 =10011112
1010112 =43
1101102 = 54
15
16.
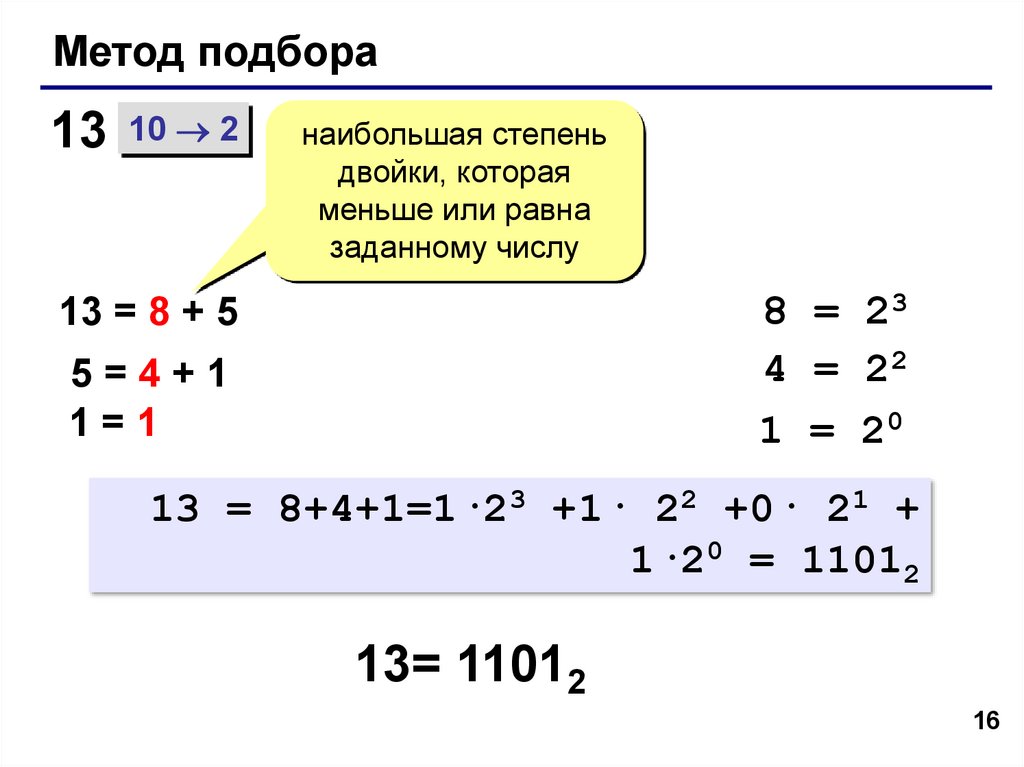
Метод подбора13 10 2
наибольшая степень
двойки, которая
меньше или равна
заданному числу
8 = 23
4 = 22
1 = 20
13 = 8 + 5
5=4+1
1=1
13 = 8+4+1=1·23 +1· 22 +0· 21 +
1·20 = 11012
13= 11012
16
17.
Перевод дробных чисел10 2
0,375 = 0,0112
0,7 = ?
0,7 = 0,101100110…
2
= 0,1(0110)2
0 ,750
0,75
Многие дробные числа нельзя представить в
виде конечных двоичных дробей.
2
1 ,50
Для их точного хранения требуется
бесконечное число разрядов.
0,5
2
Большинство дробных чисел хранится в
1 ,0
памяти с ошибкой.
2 10
1
-2
2 =
22 = 0,25
2 1 0 -1 -2 -3 разряды
101,0112 = 1·22 + 1·20 + 1·2-2 + 1·2-3
= 4 + 1 + 0,25 + 0,125 = 5,375
17
18.
Примеры:0,5625 = 0,10012
17,25 = 10001,012
18
19.
Арифметические операциисложение
вычитание
0+0=0 0+1=1 перенос0-0=0 1-1=0
1+0=1 1+1=102
1-0=1 102-1=1
заем
1 + 1 + 1 = 112
1 0 1 1 02
+ 1 1 1 0 1 12
1 0 1 0 0 0 12
0 1 1 102 0 102
1 0 0 0 1 0 12
–
1 1 0 1 12
0 1 0 1 0 1 02
19
20.
Примеры:111112
+ 1112
1001102
101112
+ 1011102
10001012
1110112
+ 110112
10101102
1110112
+ 100112
10011102
20
21.
Примеры:1011012
– 111112
11102
110012
– 112
101102
21
22.
Арифметические операцииумножение
1 0 1 0 12
1 0 12
1 0 1 0 12
+ 1 0 1 0 12
1 1 0 1 0 0 12
деление
1 0 1 0 12 1 1 12
– 1 1 12 1 1
2
1 1 12
– 1 1 12
0
22
23.
Примеры:1 0 12
1 1 02
1 1 1 1 02
1 1 1 1 1 12 1 1 12
1 0 0 12
23
24.
Домашнее задание:1452 =
3768 =
CMLXIII =
MMCXLI =
24
25.
Домашнее задание:26=
245=
1111001112 =
100012 =
25
26.
Домашнее задание:10102
+ 11112
110102
+ 10010112
1000012
- 11102
101012
- 1112
26
27.
Домашнее задание:1 0 12
1 0 02
1 0 0 0 1 1 1 12 1 1 0 1 2
27
28. Системы счисления
Тема 3. Восьмеричнаясистема счисления
29.
Восьмеричная системаОснование (количество цифр): 8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
10 8
100 8
96 12 8
8 1
4
4
100 = 1448
система
счисления
8 10
210
разряды
1448 = 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100
29
30.
Примеры:24110 =3618
758 = 6110
30
31.
Таблица восьмеричных чиселX10
X8
X2
X10
X8
X2
0
0
000
4
4
100
1
1
001
5
5
101
2
2
010
6
6
110
3
3
011
7
7
111
31
32.
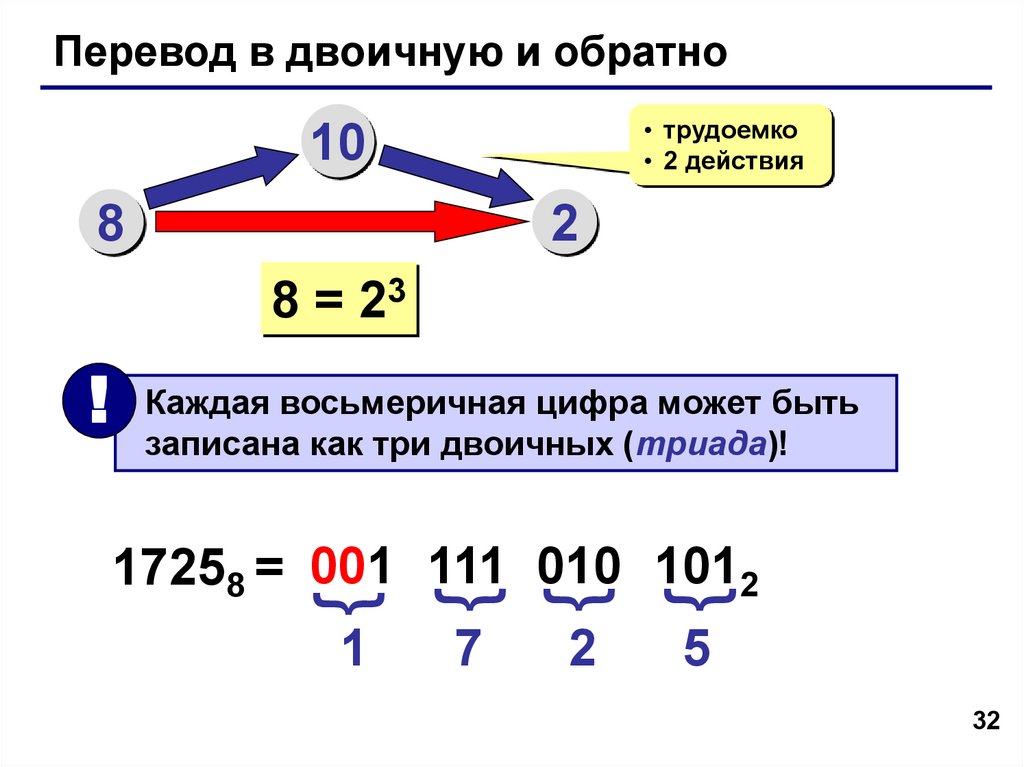
Перевод в двоичную и обратно• трудоемко
• 2 действия
10
8
2
8 = 23
! Каждая восьмеричная цифра может быть
записана как три двоичных (триада)!
{
{
{
{
17258 = 001 111 010 1012
1
7
5
2
32
33.
Примеры:34678 = 111001101112
21488 =
73528 =1110111010102
12318 = 10100110012
33
34.
Перевод из двоичной системы10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
001 001 011 101 1112
1
1
3
5
7
Ответ: 10010111011112 = 113578
34
35.
Примеры:1011010100102 = 55228
111111010112 = 37538
11010110102 = 15328
35
36.
Арифметические операциисложение
1 5 68
+ 6 6 28
1 0 4 08
36
37.
Пример6 2 58
+ 4 58
6 7 28
6 7 0 28
+ 7 78
7 0 0 18
37
38.
Арифметические операциивычитание
4 5 68
– 2 7 78
1 5 78
38
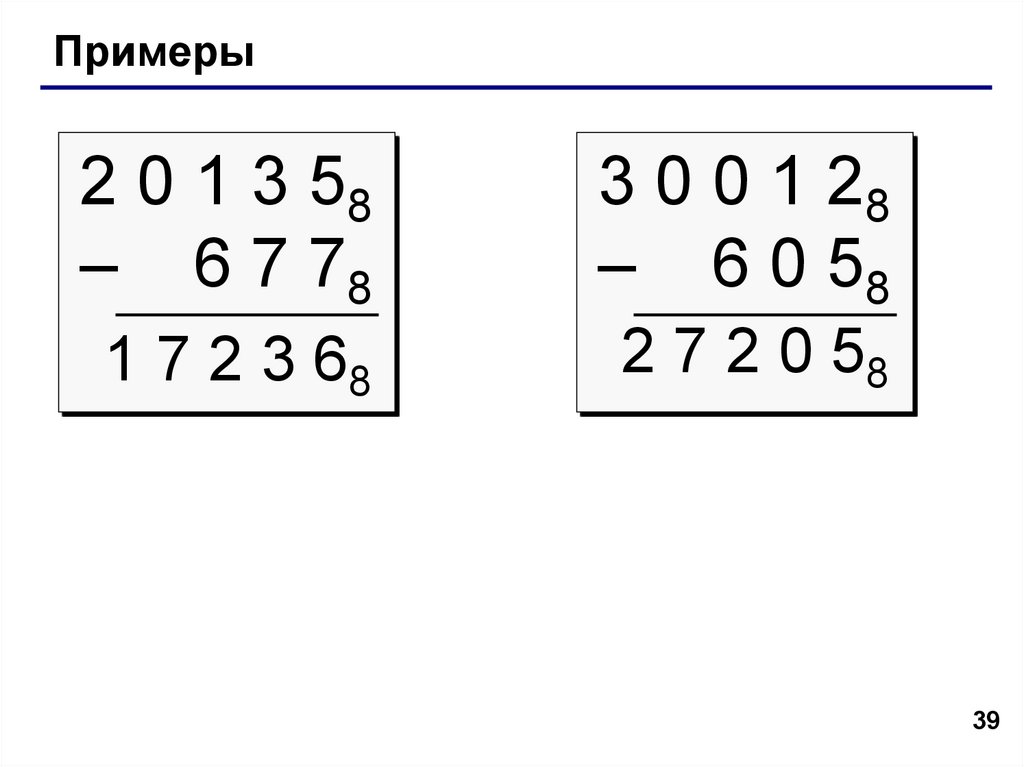
39.
Примеры2 0 1 3 58
– 6 7 78
3 0 0 1 28
– 6 0 58
1 7 2 3 68
2 7 2 0 58
39
40.
Примеры4 1 68
2 0 58
2 6 3 3 48 3 0 68
1 0 6 1 0 68
7 28
x
40
41.
4142.
4243.
Домашнее задание:256710 =
7558 =
11010100102 =
1 1 3 4 68
+ 7 7 78
6 5 4 0 08
– 6 6 6 68
43
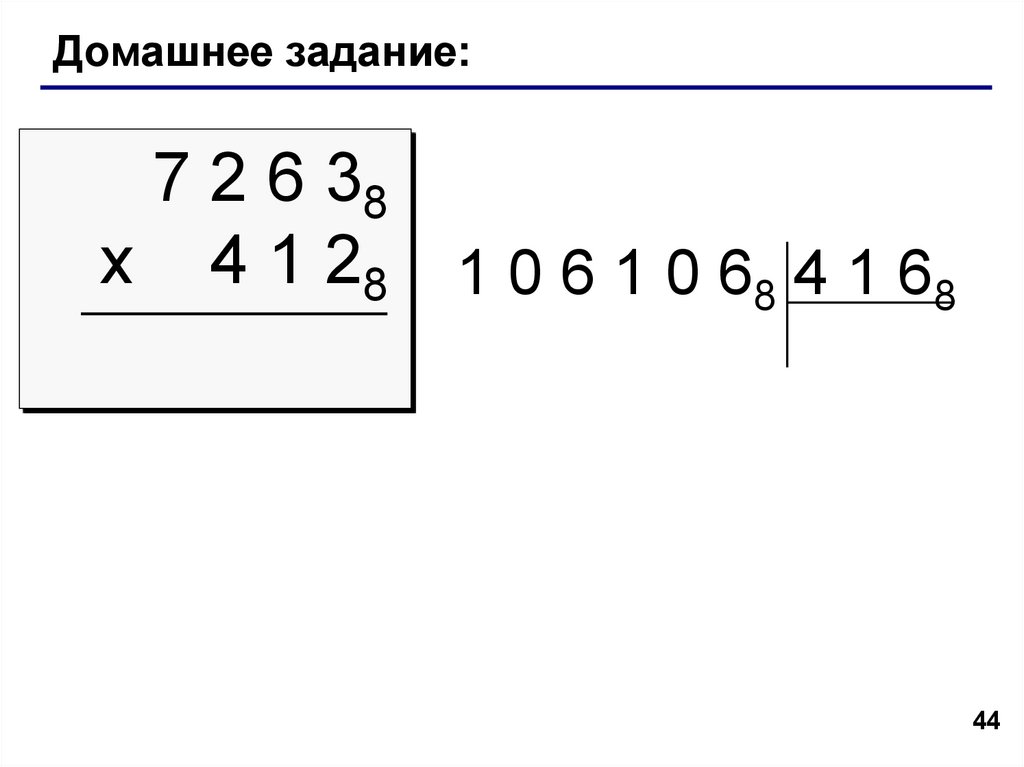
44.
Домашнее задание:7 2 6 38
x 4 1 28 1 0 6 1 0 68 4 1 68
44
45. Системы счисления
Тема 4. Шестнадцатеричнаясистема счисления
46.
Шестнадцатеричная системаОснование (количество цифр): 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10 11 12 13 14 15
10 16 107 16
96
6
107 = 6B16
11
B
система
счисления
16 10
C
1C516 = 1·162 + 12·161 + 5·160
= 256 + 192 + 5 = 453
2 1 0 разряды
46
47.
Примеры:171 = AB16
1BC16 = 444
206 = CE16
22B16 = 555
47
48.
Таблица шестнадцатеричных чиселX10
X16
X2
X10
X16
X2
0
0
0000
8
8
1000
1
1
0001
9
9
1001
2
2
0010
10
A
1010
3
3
0011
11
B
1011
4
4
0100
12
C
1100
5
5
0101
13
D
1101
6
6
0110
14
E
1110
7
7
0111
15
F
1111
48
49.
Перевод в двоичную систему• трудоемко
• 2 действия
10
16
2
16 = 24
! Каждая шестнадцатеричная цифра может быть
записана как четыре двоичных (тетрада)!
{
{
{
{
7F1A16 = 0111 1111 0001 10102
7
F
A
1
49
50.
Примеры:C73B16 = 11000111001110112
2FE116 = 101111111000012
50
51.
Перевод из двоичной системы10010111011112
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ: 10010111011112 = 12EF16
51
52.
Примеры:10101011010101102 = AB5616
1111001101111101012 = 3CDF516
1101101101011111102 = 36D7E16
52
53.
Перевод в восьмеричную и обратнотрудоемко
10
16
8
2
Шаг 1. Перевести в двоичную систему:
3DEA16 = 11 1101 1110 10102
Шаг 2. Разбить на триады:
011 110 111 101 0102
Шаг 3. Триада – одна восьмеричная цифра:
3DEA16 = 367528
53
54.
Примеры:A3516 = 50658
7658 = 1F516
54
55.
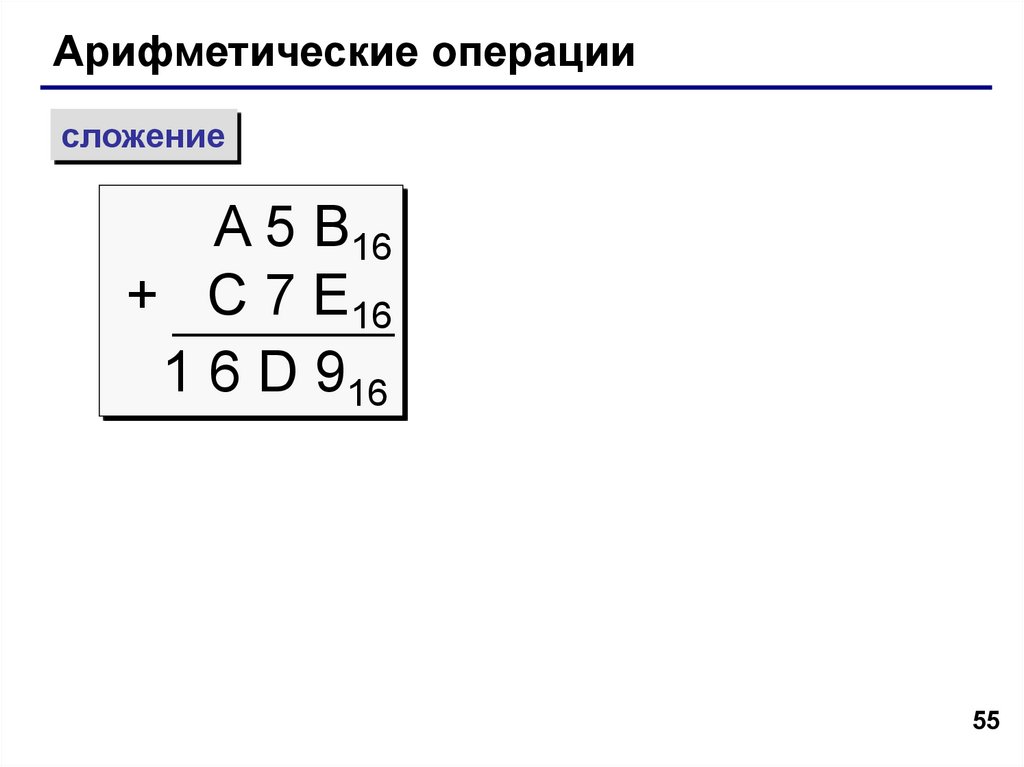
Арифметические операциисложение
A 5 B16
+ C 7 E16
1 6 D 916
55
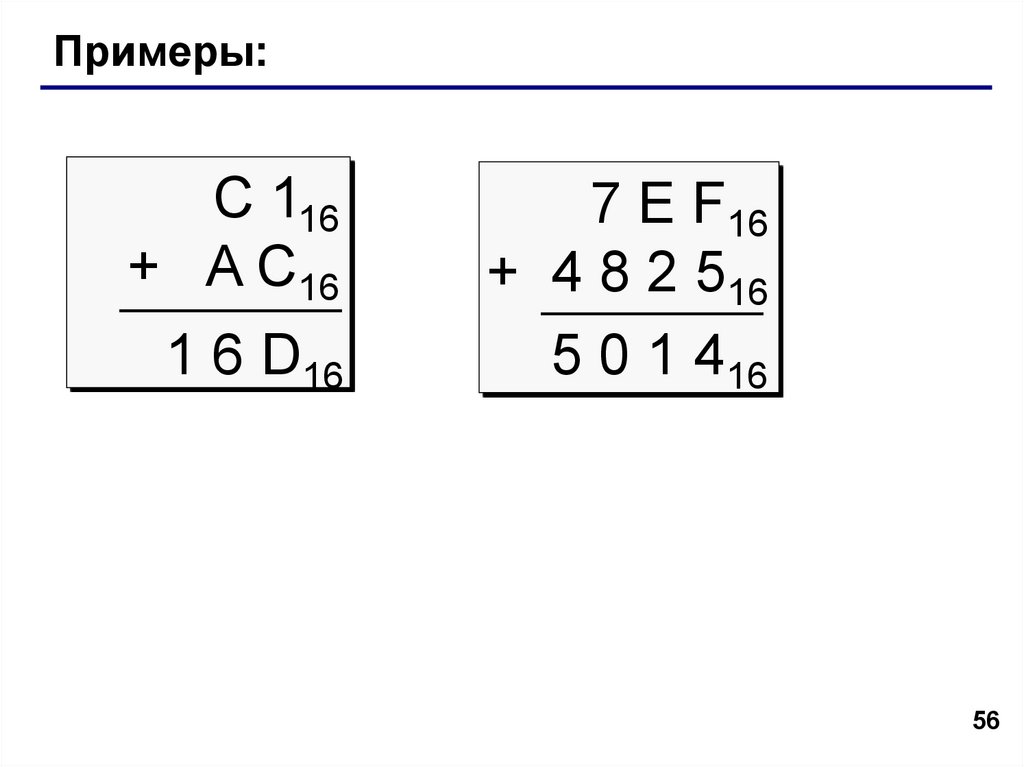
56.
Примеры:C 116
+ A C16
1 6 D16
7 E F16
+ 4 8 2 516
5 0 1 416
56
57.
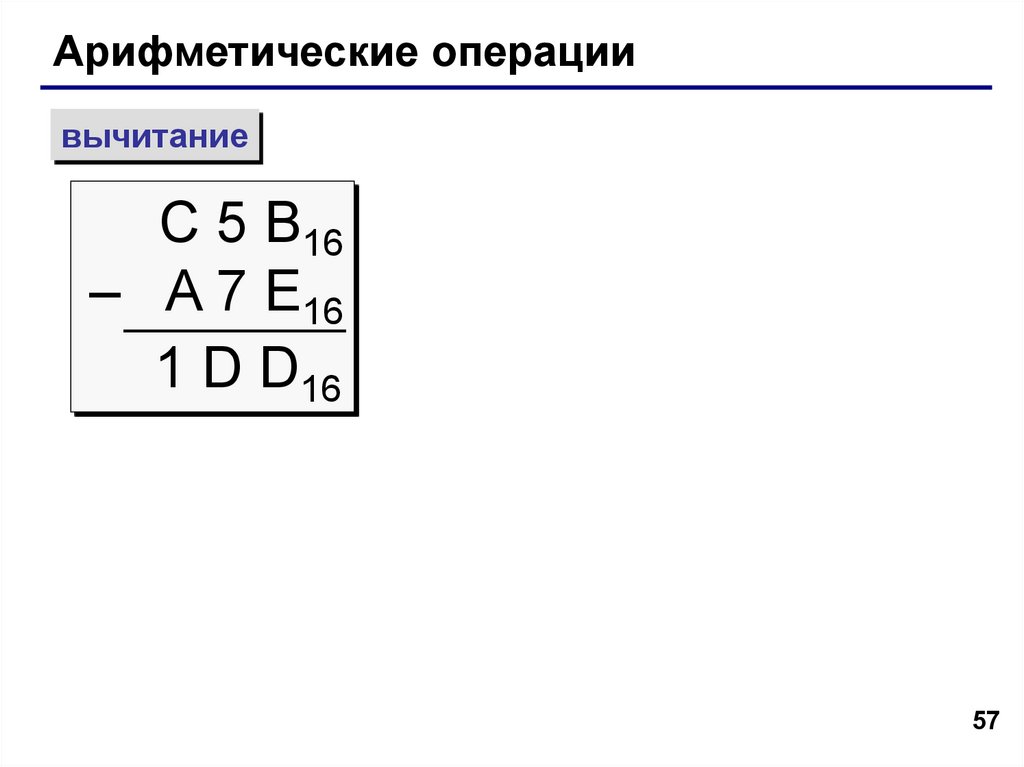
Арифметические операциивычитание
С 5 B16
– A 7 E16
1 D D16
57
58.
Пример:2 0 0 416
– C D E16
1 3 2 616
2 0 0 016
– 9 F D16
1 6 0 316
58
59.
Пример:A 4 316
x 2 0 D16
1 5 0 B 6 716
6 F 7 8 16 : 816
= D E F16
59
60.
6061.
6162.
Домашнее задание:7 8 A C 216
+ 2 0 3 F16
1 1 A 0 0 116
– B E C D16
62
63.
Домашнее задание:8 9 E16
x 1 0 0 316
4 2 B A: 1 216
63
























































 informatics
informatics








