Similar presentations:
Курс Artificial Intelligence
1.
Курс Artificial IntelligenceВсякий раз когда компьютер делает что-то, что кажется нам
разумным или рациональным, например узнает чье-то лицо на
фотографии, обыгрывает человека в какой-то игре, распознаёт
человеческий язык, когда мы говорим с нашим телефоном,
который нас понимает и отвечает всё это примеры ИИ или
искусственного интеллекта.
2.
Структура курса1. Search
2. Knowledge
3. Uncertainty
4. Optimization
5. Learning
6. Neural Networks
7. Language
3.
Поиск (Search)У нас есть искусственный интеллект и мы хотим чтобы он мог найти
решение для какой-то задачи. Может речь о том чтобы получить
маршрут движения из точки А в точку В или понять как играть в
какую-то игру (как походить например «крестиках-ноликах»).
4.
Знания KnowledgeМы хотим, чтобы наш искусственный интеллект знал информацию,
мог излагать эту информацию и что более важно, мог делать
выводы на основе этой информации. Чтобы он также мог
использовать известную ему информацию и создавать
дополнительные выводы.
5.
Неопределенность (Uncertainty)Здесь поговорим о том, что происходит если компьютер уверен в
чём-то не абсолютно, а только с определенной вероятностью. Мы
поговорим о некоторых понятиях лежащих в основе вероятности и
о том как компьютеры могут начать работать с неопределёнными
событиями, чтобы быть немного более умными и в этом.
6.
Оптимизация (Optimization)Здесь мы затронем задачи оптимизации, выполняемой
компьютером для достижения какой-либо цели, особенно когда у
компьютера может существовать несколько способов решения
задачи, в то время как нам необходим способ лучше, или, если
возможно, самый лучший.
7.
Обучение (Learning)Здесь мы поговорим о машинном обучении или обучении в целом.
Как пример когда у нас есть доступ к данным, мы можем
запрограммировать компьютеры на сложные операции, давая им
обучаться на данных и их же опыте. При наличии большего доступа
к данным они смогут выполнять задания всё лучше и лучше.
8.
Нейронные сети (Neural Networks)Компьютеры могут вдохновляться человеческими интеллектом на
примере структуры человеческого мозга. Нейронные сети могут
быть компьютерным аналогом такого рода концепций. И как,
пользуясь преимуществами определённого типа структуры
компьютерной программы мы можем написать нейронные сети,
которые способны крайне эффективно выполнять задачи.
9.
Язык (Language)• В заключение мы обратимся к языку. Но не к языку
программирования, а к человеческим языкам, на которых
говорим мы. Рассмотрим трудности, которые возникают, когда
компьютер пытается понять естественный язык и для чего могут
пригодиться некоторые из процессов обработки естественного
языка, происходящих в современном искусственном интеллекте.
10.
Лекция 1.ПоискSearch
11.
Постановка задачи• Задача заключается в том, чтобы попытаться понять, что делать
когда у нас есть какая-то ситуация, в которой находится
компьютер, то есть какая-то среда в которой находится агент. Мы
хотим чтобы агент мог каким-то образом искать решения
проблемы.
12.
«Пятнашки»13.
Поиск пути в лабиринте14.
Яндекс.Карты15.
Searsh Problems• Поразмышляем об этих типах переборных задач и о том, что
входит в решение такой задачи, чтобы ИИ мог найти хорошее
решение. Для этого нам нужно будет ввести несколько терминов.
16.
Агент (Agent)Агент - это сущность, воспринимающая свою окружающую среду.
Она способна воспринимать вещи вокруг себя и каким-то образом
воздействовать на них.
17.
Состояние (State)• Состояние - это конфигурация агента в окружающей его
среде.
18.
Начальное состояние (Initial state)• Начальное состояние это состояние, из которого начинает агент.
Это такое состояние из которого мы собираемся начать. Это будет
отправной точкой для нашего алгоритма поиска.
19.
Действия (Actions)Действие - это выбор, который мы можем сделать в любом заданном
состоянии. В случае с ИИ мы будем определять эти понятия точнее, чтобы
программировать более математически. Действия будут повторяться,
поэтому мы можем определить действие как функцию.
Actions(s)
где s – некоторое состояние, существующее внутри нашей среды.
Функция Actions(s) будет принимать состояние S в качестве входных данных и
возвращать в качестве выходных данных набор всех действий, которые могут
быть выполнены в этом состоянии.
20.
Допустимые действияМожет быть так, что некоторые действия допустимы только для
определённых состояний.
• Нашему ИИ, нужен код состояния и
код действия.
• Но также будет нужен и код
отношений между этими вещами как состояние и действия
соотносятся друг с другом.
21.
Модель перехода (Transition model)Модель перехода будет описывать в какое состояние мы попадаем
после выполнения некоторого доступного действия в каком-то
другом состоянии.
Result (s, a)
s – состояние, а - действие.
Выходные данные функции Result дадут нам состояние, которое
мы получим после выполнения действия а в состоянии s.
22.
Пример модели перехода в «15»Result (
,
)=
функция Result должна разбираться как использовать состояние и
действие и какие получить результаты.
23.
Пространство состояний (State space)Пространство состояний это множество всех состояний, которые
мы можем получить из начального состояния с помощью любой
последовательности действий добавив к ней ноль, одно, два или
более действий.
24.
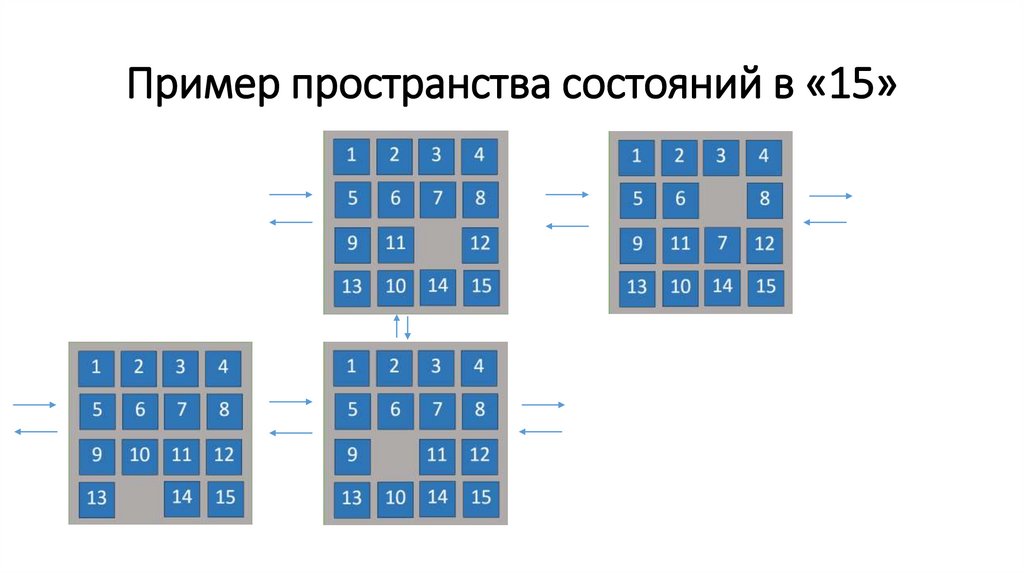
Пример пространства состояний в «15»25.
Граф состоянийЭто абстрактное обозначение изображает ту же самую идею.
Каждый из этих небольших кружков-узлов представляет собой
одно из состояний в рамках нашей задачи. Стрелки обозначают
действия, которые мы можем выполнить в каждом конкретном
состоянии. Так мы переходим из одного состояния в другое.
26.
Тест цели (goal test)Тест цели представляет собой некий способ определения, является
ли данное состояние целевым.
В случае вроде построения маршрута движения - это довольно легко.
Если вы в состоянии которое пользователь ввёл как «место
назначения» - то понимаете что находитесь в целевом состоянии. В
игре в «15» надо проверять, что числа расположены в порядке
возрастания.
ИИ нужно какое-то кодирование, чтобы он понял является ли то
состояние, в котором он находится – целью.
27.
Стоимость пути (path cost)При формулировании переборных задач каждому пути мы будем
присваивать вычислительную стоимость - какое это число, которое
сообщает насколько затратен этот конкретный вариант. А затем мы
сообщим ИИ, что надо искать не просто решение, какой-то способ
перехода от начального состояния к цели, а решение, которое
минимизирует стоимость этого пути. Менее затратное,
занимающее меньше времени или минимизирующее какое-то
другое числовое значение.
28.
Пример path costКаждая из этих стрелок, каждое из этих действий, которые мы
можем выполнить имеют какое-то связанное с ними число,
которое является стоимостью пути этого конкретного действия и
затраты на одно действие могут быть больше чем на какое-то
другое.
29.
Составляющие «Search Problems»1. Initial state
2. Actions
3. Transition model
4. Goal test
5. Path cost function
30.
Оптимальное решение (Optimal solution)Цель, в конечном счёте, состоит в том, чтобы найти решение.
В идеале, мы хотели бы найти не любое решение, а оптимальное,
имеющее наименьшую стоимость пути среди всех возможных
решений.
31.
Узел (node)Узел - это структура данных, которая фиксирует множество
различных значений. В частности для переборной задачи она будет
фиксировать четыре. Каждый узел будет фиксировать:
1. State - состояние в котором мы находимся;
2. Parent - родительский узел;
3. Action - какое действие мы выполнили, чтобы попасть из
родительского узла в текущее состояние.
4. Path cost - стоимость пути. Число, указывающее на то насколько
длинным был путь из начального состояния до нынешнего.
32.
ФронтирПри нахождении в данном состоянии у нас есть несколько
вариантов, которые мы могли бы выбрать и мы собираемся их
исследовать. И как только мы их исследуем, то обнаружим, что
перед нами предстало ещё больше вариантов. Мы учтём все эти
доступные варианты и сохраним их внутри единой структуры
данных, которую назовём фронтир.
Фронтир - всё то, что мы могли бы исследовать, но ещё не
исследовали или не посетили.
33.
Алгоритм поиска (Approach)• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение найдено
• Else разворачиваем узел – добавляем все вытекающие из
него узлы во фронтир.
34.
Пример поиска пути из A до E (шаг 1)Фронтир
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
35.
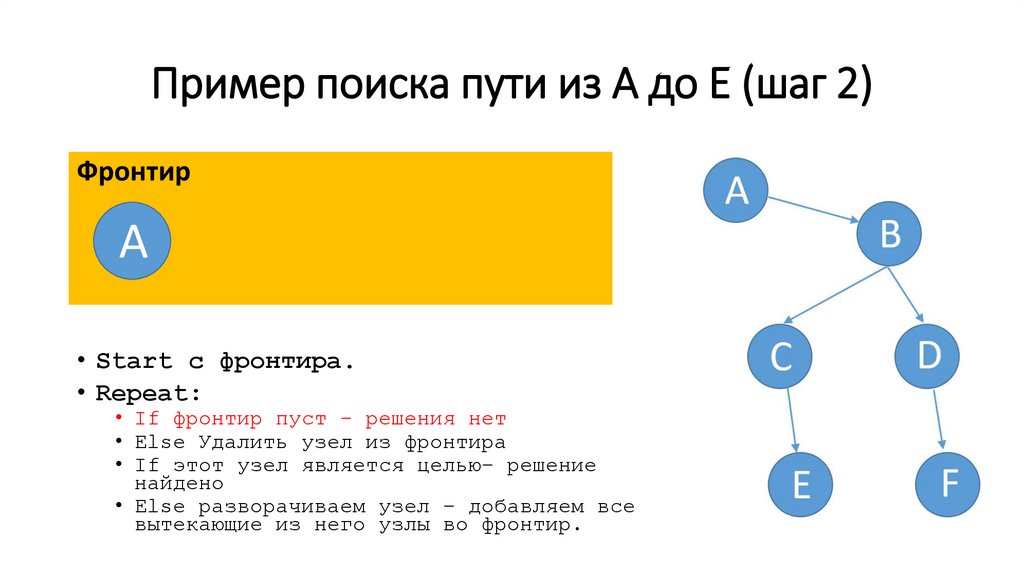
Пример поиска пути из A до E (шаг 2)Фронтир
A
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
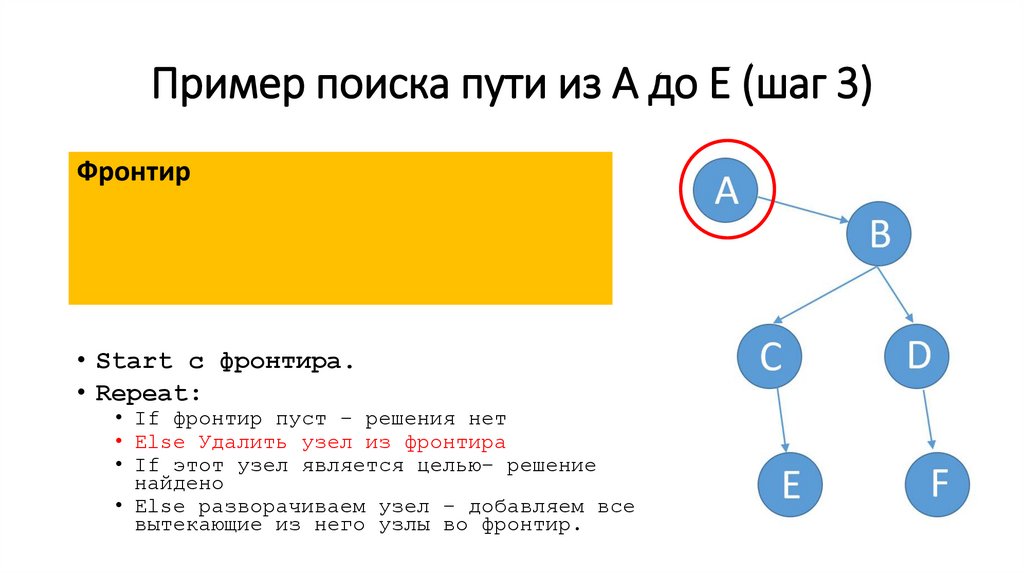
36.
Пример поиска пути из A до E (шаг 3)Фронтир
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
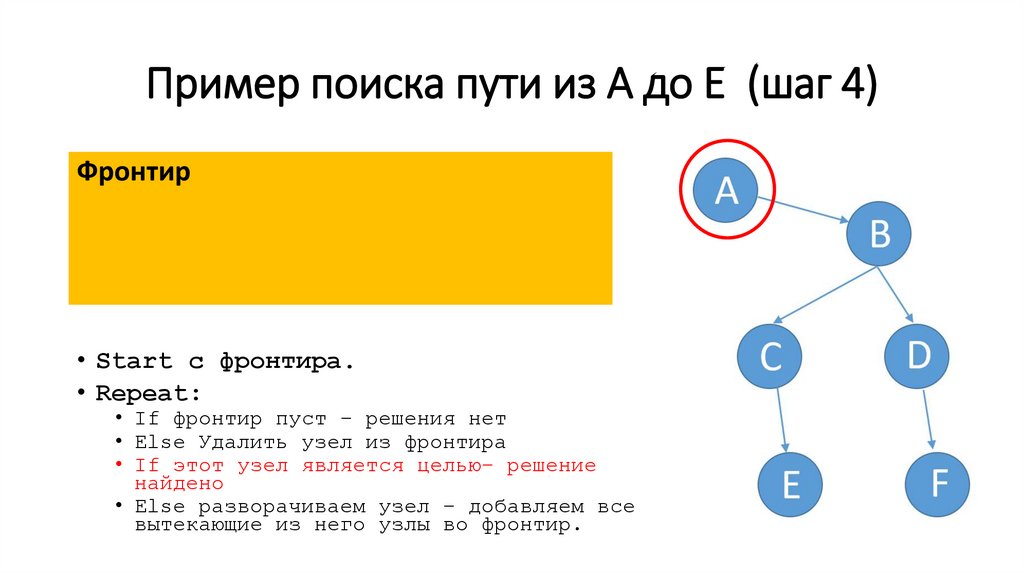
37.
Пример поиска пути из A до E (шаг 4)Фронтир
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
38.
Пример поиска пути из A до E (шаг 5)Фронтир
В
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
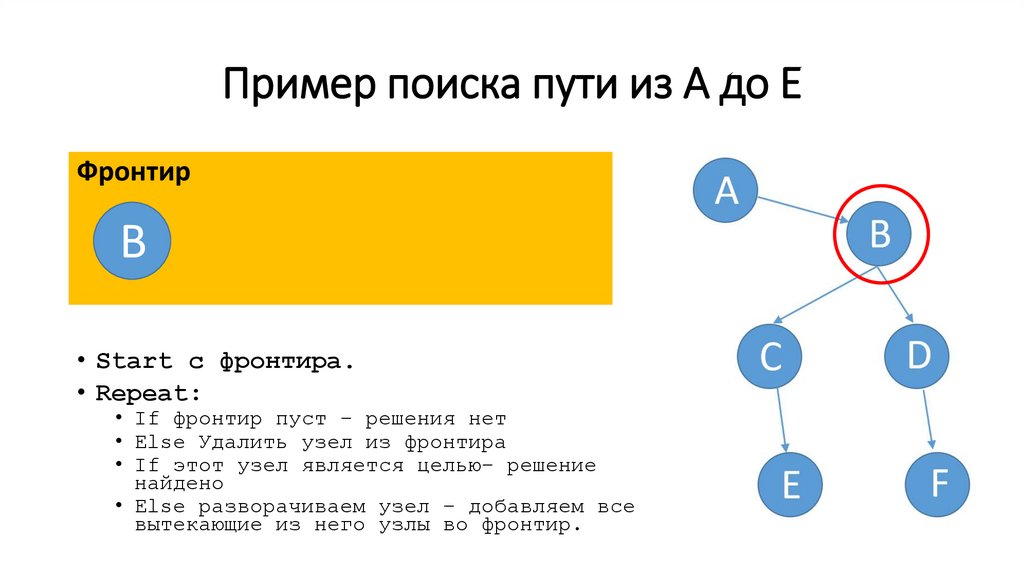
39.
Пример поиска пути из A до EФронтир
В
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
40.
Пример поиска пути из A до EФронтир
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
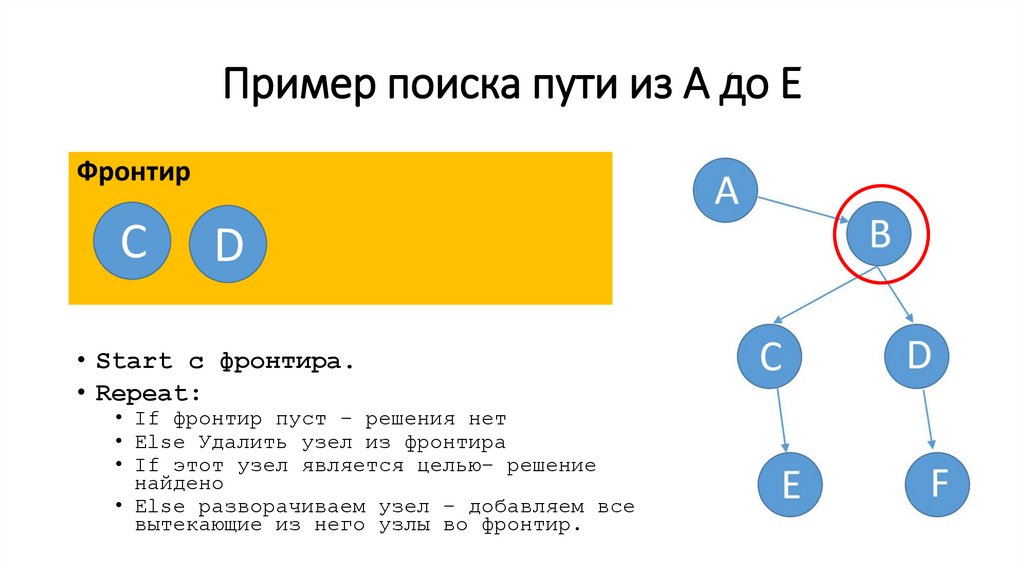
41.
Пример поиска пути из A до EФронтир
С
D
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
42.
Пример поиска пути из A до EФронтир
D
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
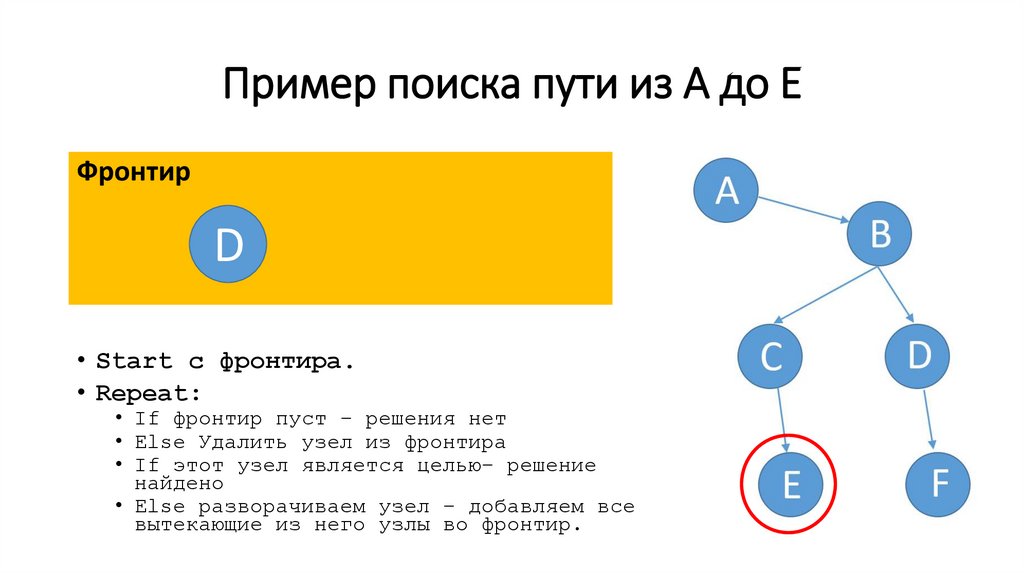
43.
Пример поиска пути из A до EФронтир
E
D
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
44.
Пример поиска пути из A до EФронтир
D
• Start c фронтира.
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью– решение
найдено
• Else разворачиваем узел – добавляем все
вытекающие из него узлы во фронтир.
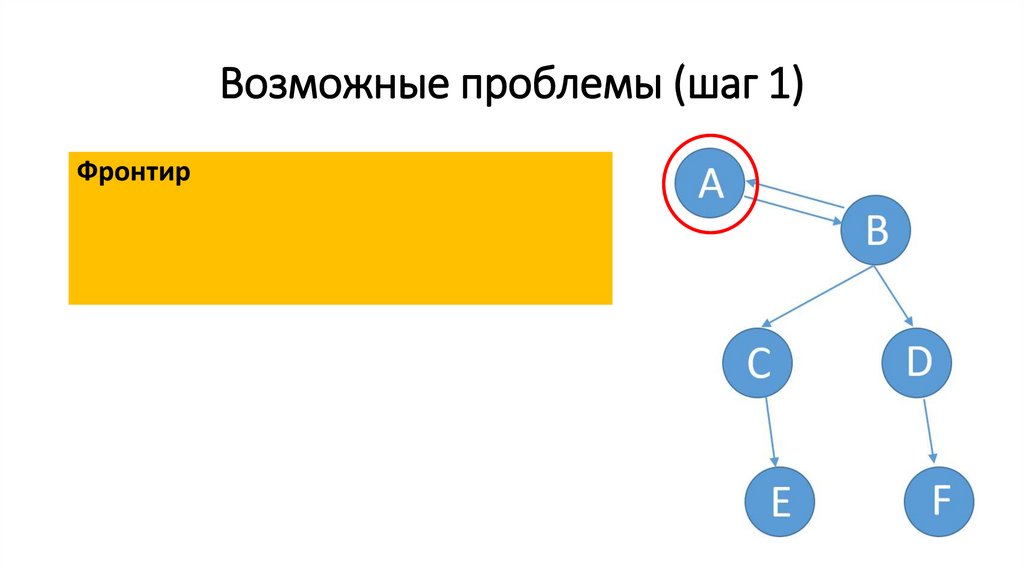
45.
Возможные проблемы (шаг 1)Фронтир
46.
Возможные проблемы (шаг 2)Фронтир
В
47.
Возможные проблемы (шаг 3)Фронтир
A
C
D
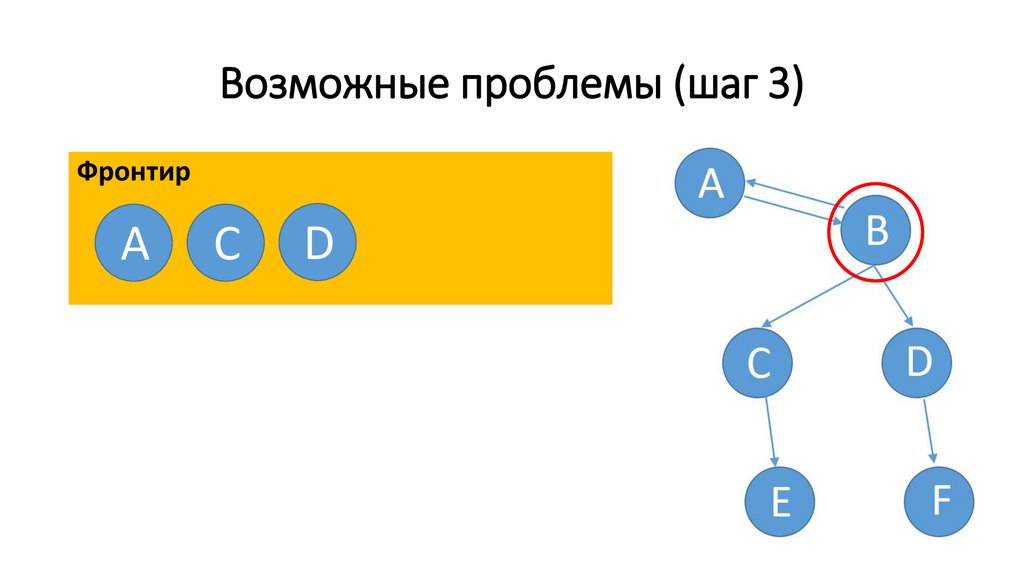
48.
Возможные проблемы (шаг 4)Фронтир
C
D
49.
Улучшенный подход (Revised Approach)• Start c фронтира.
• Start c пустым сетом исследованных узлов
(explored set)
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью – решение найдено
• Add узел в сет исследованных (explored set)
• Else разворачиваем узел – добавляем все вытекающие
из него узлы во фронтир.
50.
Порядок исключения узлов• Start c фронтира.
• Start c пустым сетом исследованных узлов
(explored set)
• Repeat:
• If фронтир пуст – решения нет
• Else Удалить узел из фронтира
• If этот узел является целью – решение найдено
• Add узел в сет исследованных (explored set)
• Else разворачиваем узел – добавляем все вытекающие
из него узлы во фронтир.
51.
Стек (stack)Стек работает по принципу последний пришел – первый ушел
Last-in first-out
52.
Пример поиска пути из A до E (шаг 1)Фронтир
A
Еxplored set
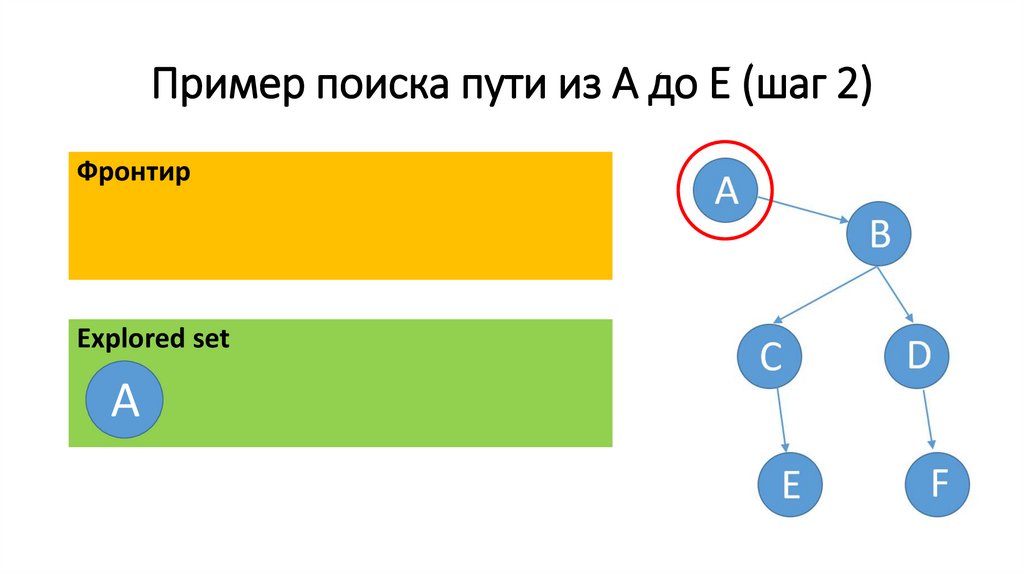
53.
Пример поиска пути из A до E (шаг 2)Фронтир
Еxplored set
A
54.
Пример поиска пути из A до E (шаг 3)Фронтир
В
Еxplored set
A
55.
Пример поиска пути из A до E (шаг 4)Фронтир
C
D
Еxplored set
A
В
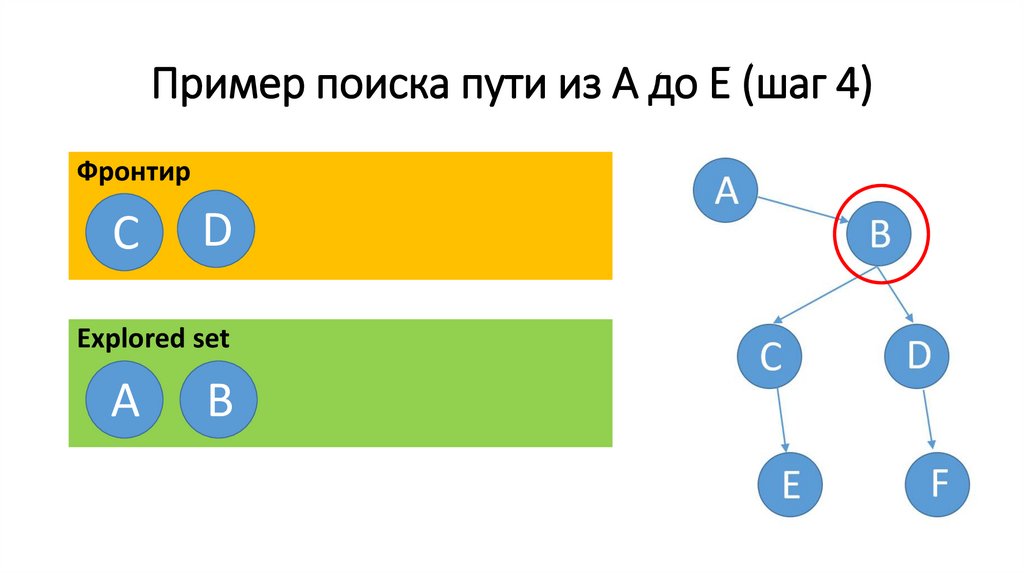
56.
Пример поиска пути из A до E (шаг 5)Фронтир
C
Еxplored set
A
В
D
57.
Пример поиска пути из A до E (шаг 6)Фронтир
C
F
Еxplored set
A
В
D
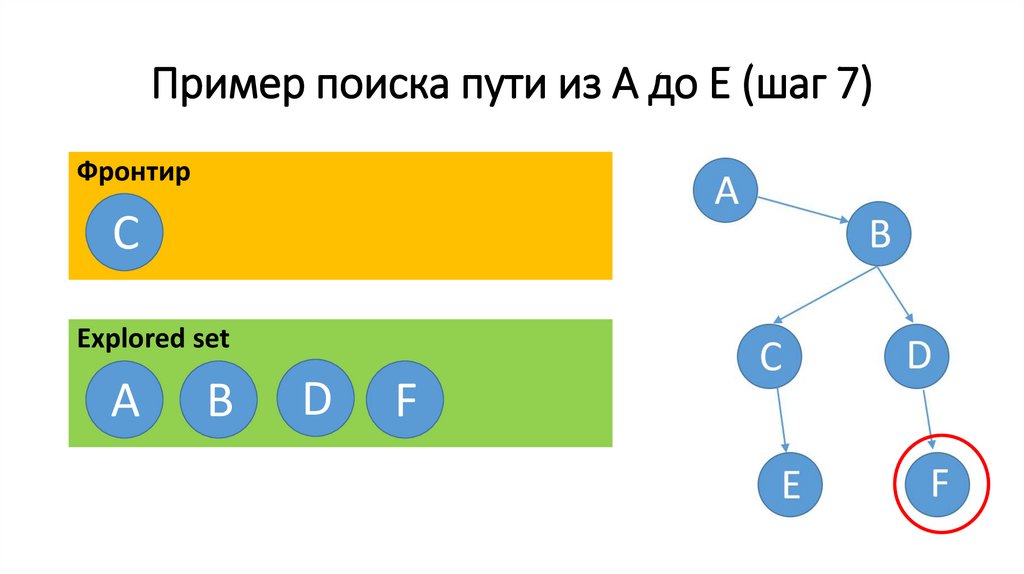
58.
Пример поиска пути из A до E (шаг 7)Фронтир
C
Еxplored set
A
В
D
F
59.
Пример поиска пути из A до E (шаг 8)Фронтир
Е
Еxplored set
A
В
D
F
C
60.
Поиск в глубину (Depth-First Search)Поиск в глубину - это алгоритм поиска, при котором мы исследуем
самый глубокий узел во фронтире. Мы продвигаемся вглубь
нашего дерева поиска, а затем, когда упираемся в тупик
возвращаемся назад и пробуем другой вариант.
61.
Поиск в ширину (Breadth-First Search)Поиск в ширину будет исследовать самый поверхностный узел во
фронтире. При поиске в глубину мы использовали стек и
исследовали тот элемент который был добавлен во фронтир
последним, а поиске в ширину вместо стека будет использоваться
очередь работающая по принципу первой пришёл первый ушёл,
где мы будем рассматривать первый элемент добавленный во
фронтир.
62.
Очередь (queue)Основной принцип - first-in first-out. Узлы образуют очередь и те
что попали во фронтир первыми и будут исследованы первыми.
63.
Пример поиска пути от А до Е на основеqueue (шаг 1)
Фронтир
Еxplored set
A
64.
Пример поиска пути от А до Е на основеqueue (шаг 2)
Фронтир
С
D
Еxplored set
A
В
65.
Пример поиска пути от А до Е на основеqueue (шаг 3)
Фронтир
D
Еxplored set
A
В
С
66.
Пример поиска пути от А до Е на основеqueue (шаг 5)
Фронтир
D
Е
Еxplored set
A
В
С
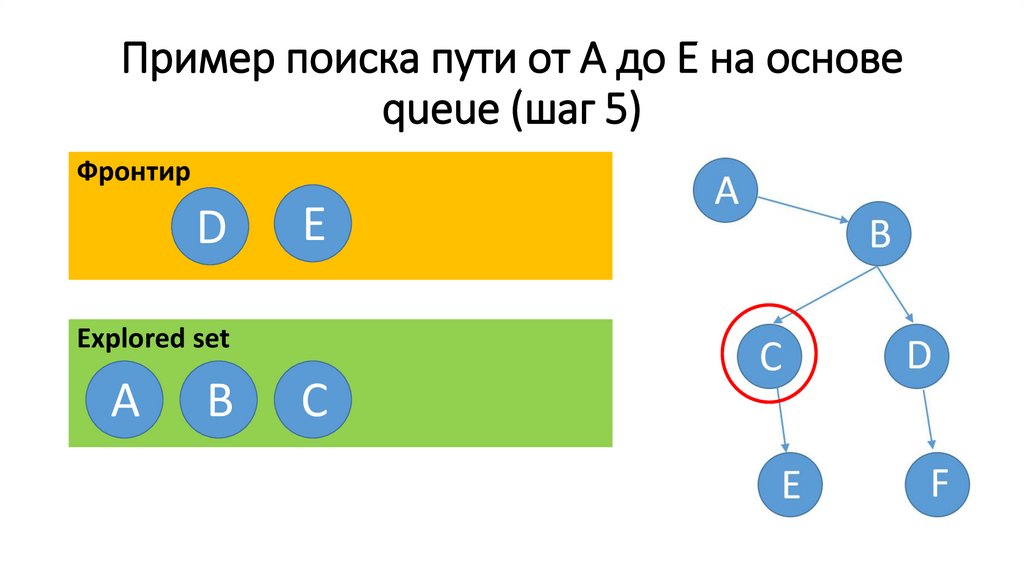
67.
Пример поиска пути от А до Е на основеqueue (шаг 5)
Фронтир
Е
F
С
D
Еxplored set
A
В
68.
Пример поиска пути от А до Е на основеqueue (шаг 6)
Фронтир
F
Еxplored set
A
В
С
D
69.
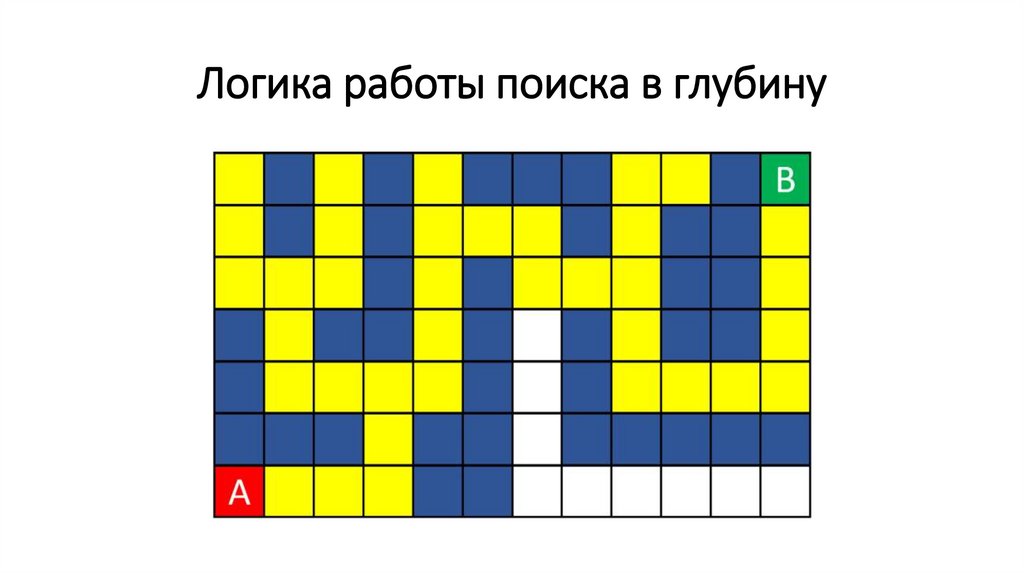
Применение Depth-First Search к поискупути в лабиринте
70.
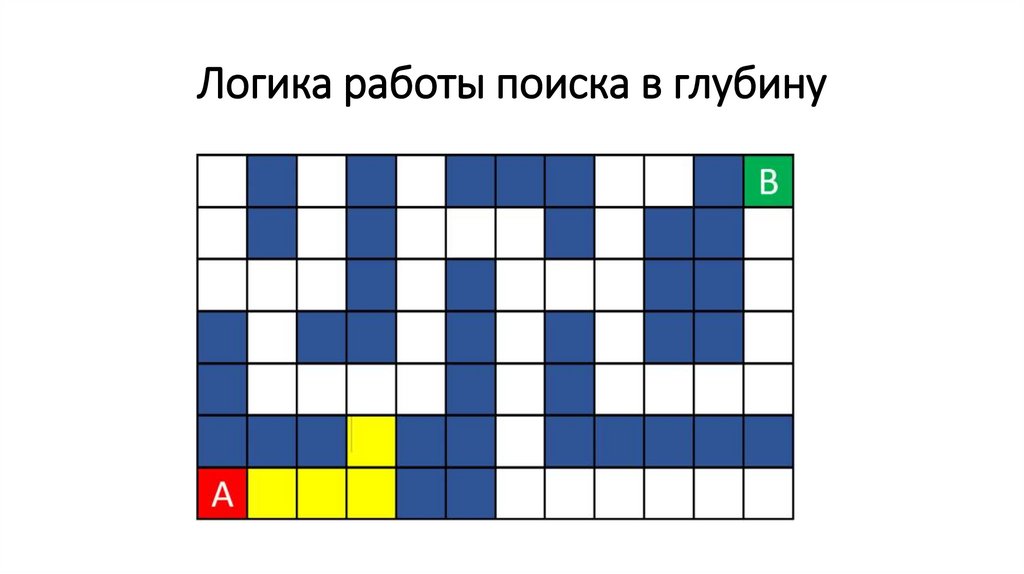
Логика работы поиска в глубину71.
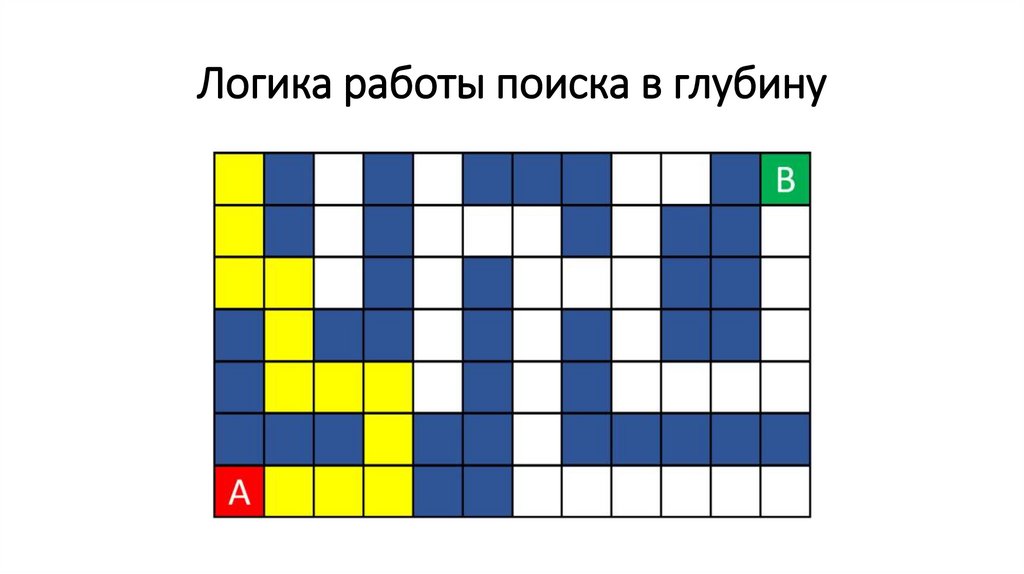
Логика работы поиска в глубину72.
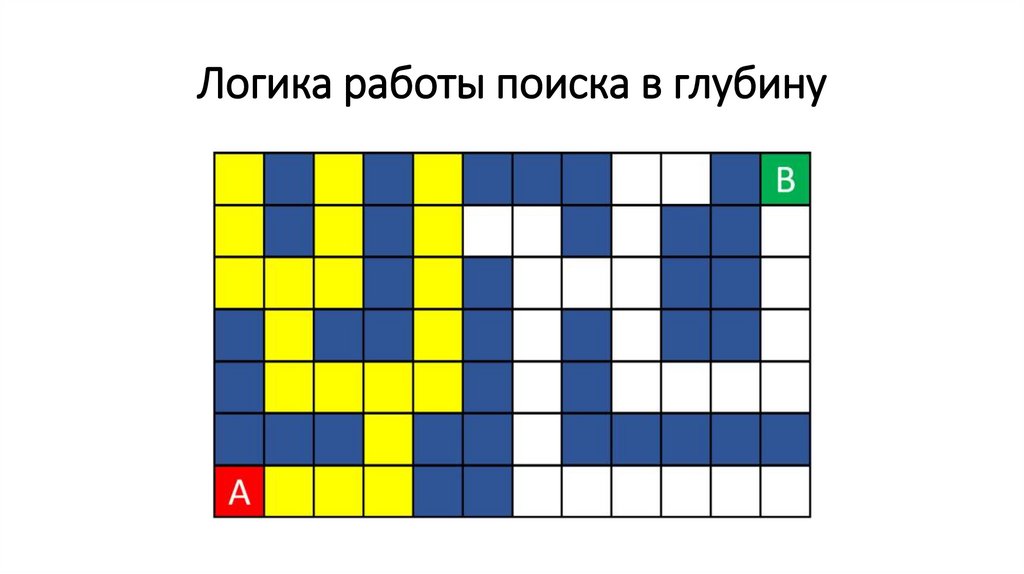
Логика работы поиска в глубину73.
Логика работы поиска в глубину74.
Логика работы поиска в глубину75.
Логика работы поиска в глубину76.
Резюме работы поиска в глубину1. всегда ли будет срабатывать этот алгоритм? Всегда ли он будет
способен найти путь от исходного состояния к целевому?
2. будет ли это хорошее решение? Является ли это решение
самым оптимальным?
77.
Работа Depth-First Search в лабиринте с«петлей»
78.
Применение Breadth-First Searchк поискупути в лабиринте
79.
Применение Breadth-First Searchк поискупути в лабиринте
80.
Применение Breadth-First Searchк поискупути в лабиринте
81.
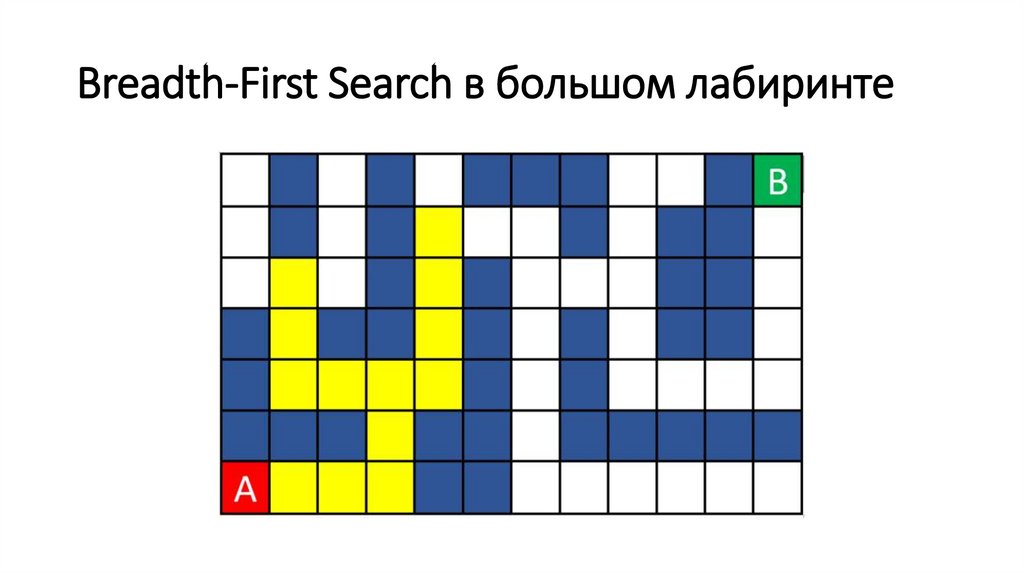
Breadth-First Search в большом лабиринте82.
Breadth-First Search в большом лабиринте83.
Breadth-First Search в большом лабиринте84.
Breadth-First Search в большом лабиринте85.
Breadth-First Search в большом лабиринте86.
Пример. Класс Node87.
Пример.Класс
StackFrontier
88.
Пример. Класс QueueFrontier89.
Пример. Класс Maze90.
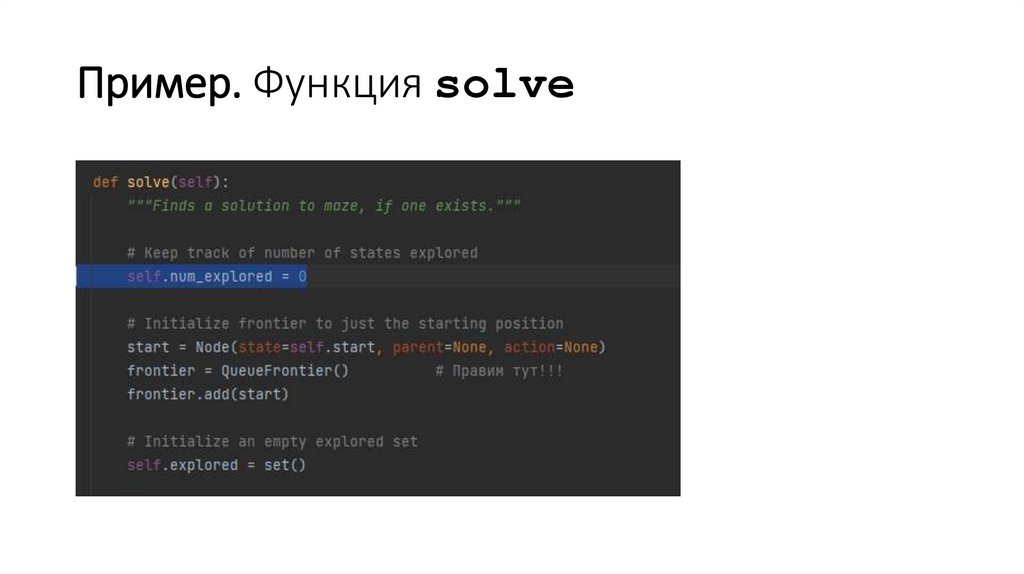
Пример. Функция solve91.
Пример.Функция solve.
Цикл
92.
Пример. Оценка пути93.
Добавление соседей во фронтир94.
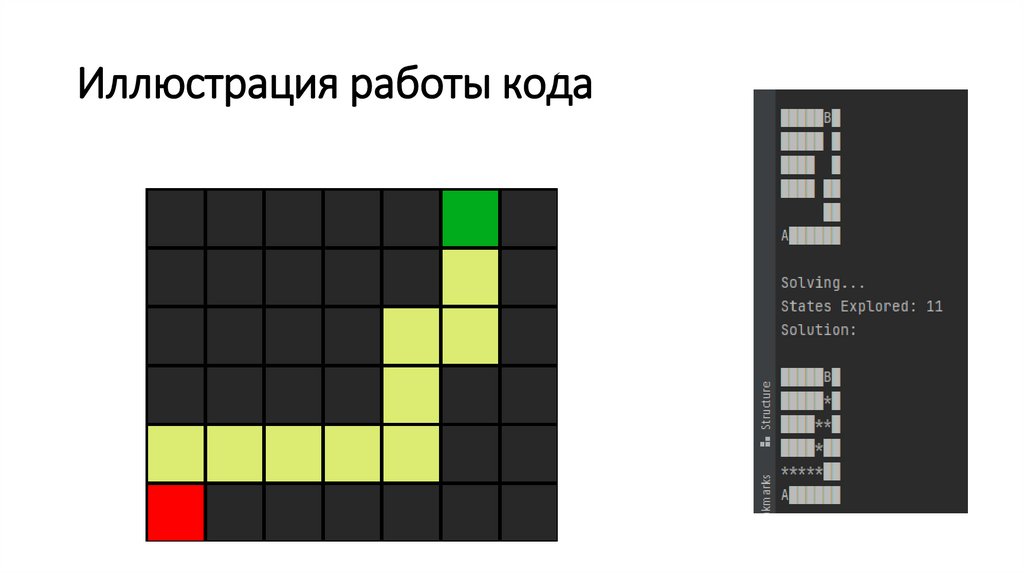
Иллюстрация работы кода95.
Depth-First Searchи сложный лабиринт
96.
Трудоемкость Depth-First Search97.
Трудоемкость Depth-First Search5. Здесь пришлось
впустую исследовать
всю эту верхнюю
часть
4. Здесь ему
опять не повезло
3. Здесь ему
повезло потому
что он не выбрал
это направление
1. Он начал изучать
вот это направление.
2. Исследовал весь путь до самого конца
даже эту длинную и извилистую часть.
98.
Breadth-First Search и сложный лабиринт99.
Трудоемкость Breadth-First Search100.
Лабиринт с петлей Breadth-First Search101.
Лабиринт с петлей Depth-First Search102.
Резюме• Является ли алгоритм Breadth-First Search
лучшим вариантом, который будет находить
для нас оптимальное решение и нам не
придётся беспокоиться о тех случаях, когда
найденный путь не будет являться самым
коротким?
• Если цель находится далеко от начального
состояния нам может понадобиться
выполнить много шагов чтобы добраться до
цели и тогда может получиться так, что
алгоритм поиска в ширину в конечном итоге
исследует весь граф, пройдет по всем
ячейкам лабиринта в поисках решения.
103.
Делаем алгоритм «более умным»3. Поиск в ширину
использовал другой
подход. Он
исследовал все
ближайшие
поверхностные
элементы, исследовал
по шагу слева и
справа снова и снова
2. Поиск в глубину,
выбрал один путь и
решил бы исследовать
его до самого конца
1. Первая точка принятия
решения была здесь
104.
Логика человекаКак бы повел
себя человек
на такой
развилке?
105.
Неинформированные алгоритмы поиска(uninformed search)
• К не информированным типам поиска относятся алгоритмы
поиска в глубину и в ширину, которые мы только что
рассматривали. Это такая стратегия поиска при которой
специфические знания о задаче не используютс. При поиске в
глубину или в ширину для решения лабиринта по-сути не важна
его структура или какие-либо ещё его свойства. Они просто
обращаются к доступным действиям. я для её решения.
106.
Информированные алгоритмы поиска(informed search)
• Информированный метод поиска это стратегия поиска, которая
использует специфические знания о задаче с целью нахождения
её решения. В случае с лабиринтом конкретные знания о задаче
заключается в том, что если я нахожусь в квадрате, который по
расположению ближе к цели, то это лучше чем находиться в
квадрате, который по расположению дальше.
«жадный поиск по первому наилучшему соответствию»
107.
Жадный поиск по первому наилучшемусоответствию (greedy best-first search)
• Жадный поиск по первому наилучшему соответствию - это
алгоритм, который в отличие от поиска в глубину, исследующего
до самого дальнего узла или в отличие от поиска в ширину,
исследующего самый близкий и поверхностный узел, исследует
тот узел, который кажется ему ближайшим к цели.
• Эвристический подход является способом оценки того
действительно ли мы близки к цели. Мы будем использовать
эвристическую функцию, которая обычно называется h(n). В
качестве входных данных она использует состояние, а возвращает
оценку того находимся ли мы близко к цели.
108.
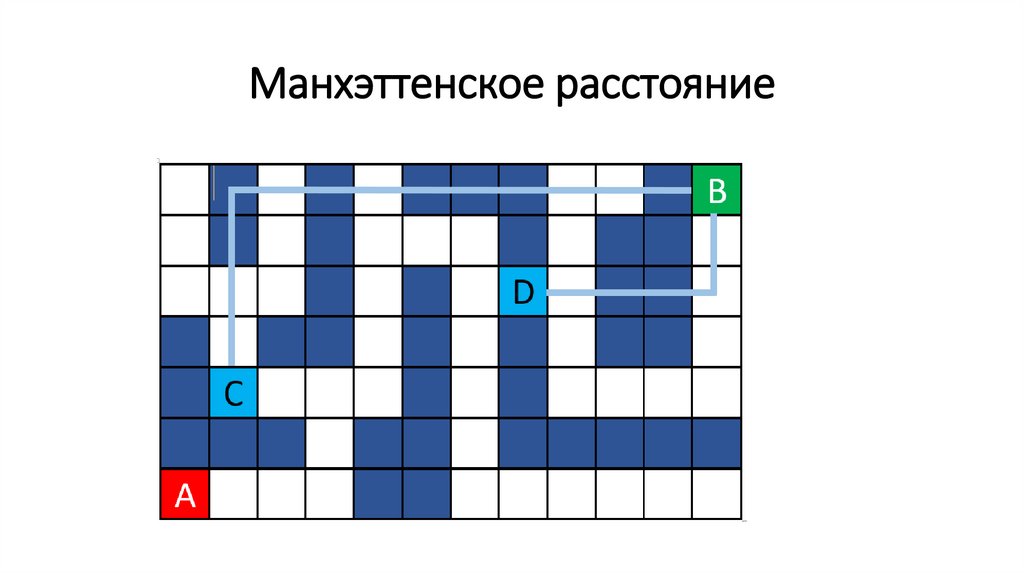
Эвристическая функция (heuristic function)109.
Манхэттенское расстояние110.
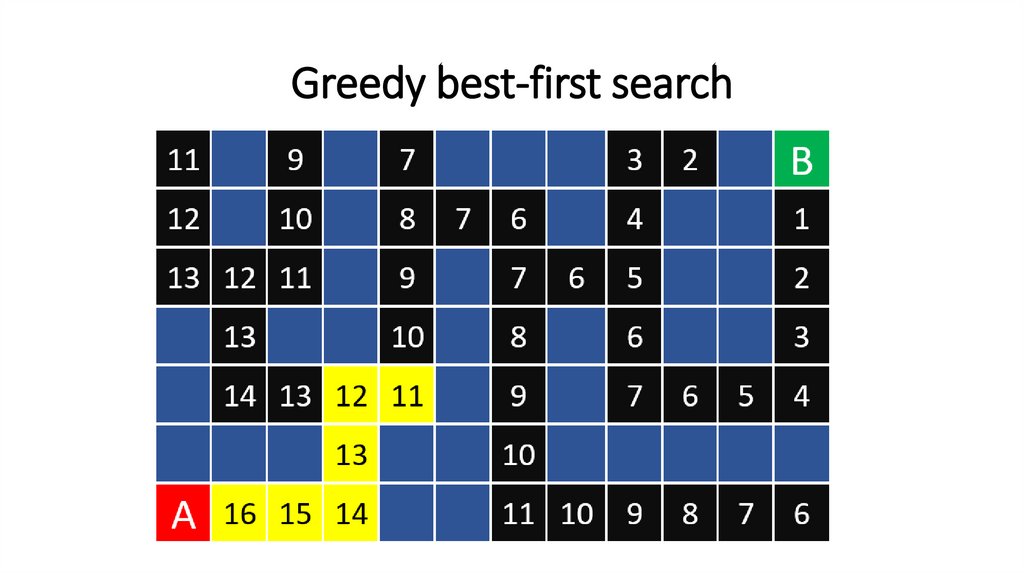
Greedy best-first search111.
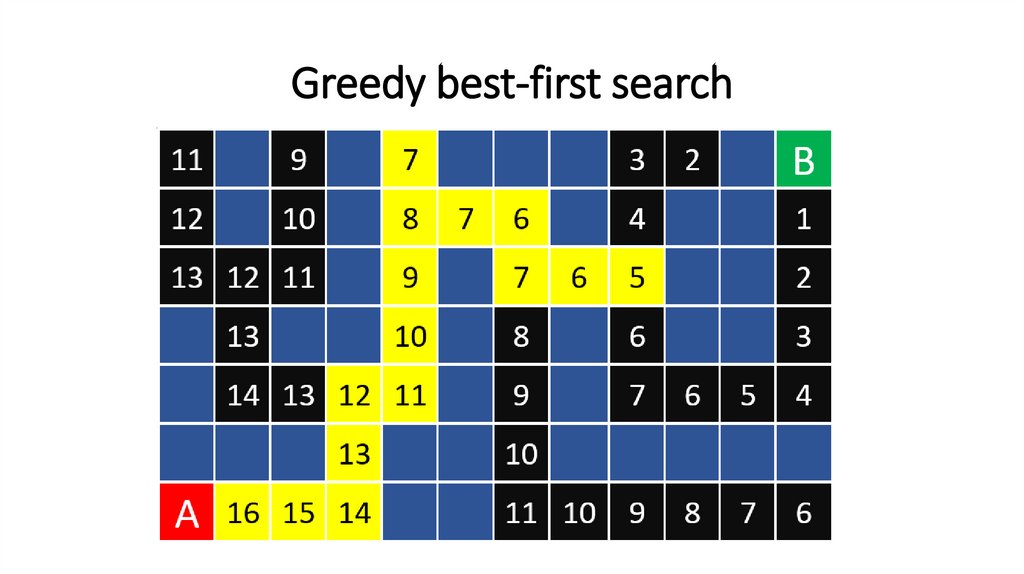
Greedy best-first search112.
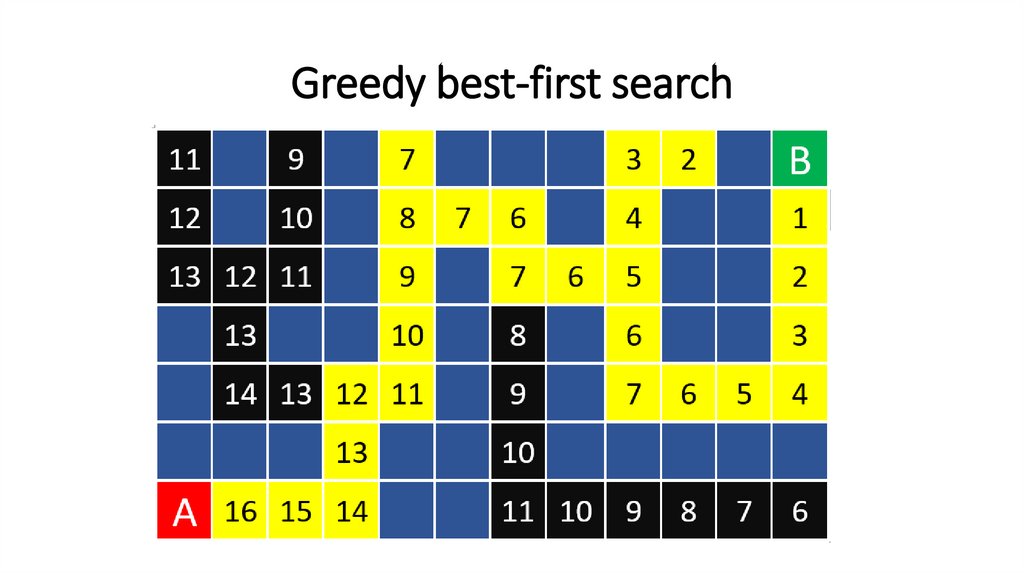
Greedy best-first search113.
Greedy best-first search114.
Greedy best-first search115.
Greedy best-first search116.
Greedy best-first search117.
Greedy best-first search118.
РезюмеBreadth-First Search
Greedy best-first search
Является ли этот алгоритм оптимальным? Сможет ли он
всегда находить кратчайший путь от начального
состояния к целевому?
119.
Лабиринт с петлей и Greedy best-first searchздесь
находится
точка
принятия
решения
120.
Лабиринт с петлей и Greedy best-first searchВот что подразумевается, когда
мы говорим «жадный алгоритм».
121.
Резюме• Идея эвристической функции хороша. С ней мы можем оценить
расстояние от нас до цели. Благодаря этому мы можем сделать
более удачный выбор, избежать необходимости исследовать
целые части пространства состояний. Но нам всё ещё надо
модифицировать алгоритм, чтобы получать оптимальный
результат.
• Каким образом мы можем это сделать? Какой интуицией
руководствоваться здесь?
122.
Модификация алгоритма поискаПоиск по первому
наилучшему соответствию
принял решение здесь и
пошёл по длинному пути.
Если мы проследуем
согласно алгоритму - то
придем к 12
123.
А* searchБудем развёртывать узел с наименьшим значением:
g(n) + h(n)
• h(n) - это всё та же эвристическая функция, которую мы
разбирали. Она будет изменяться в зависимости от задачи.
• g(n) - это стоимость пути для достижения узла. То есть, сколько
шагов я сделал, чтобы оказаться в текущем положении.
124.
Иллюстрация алгоритма поиска А* search125.
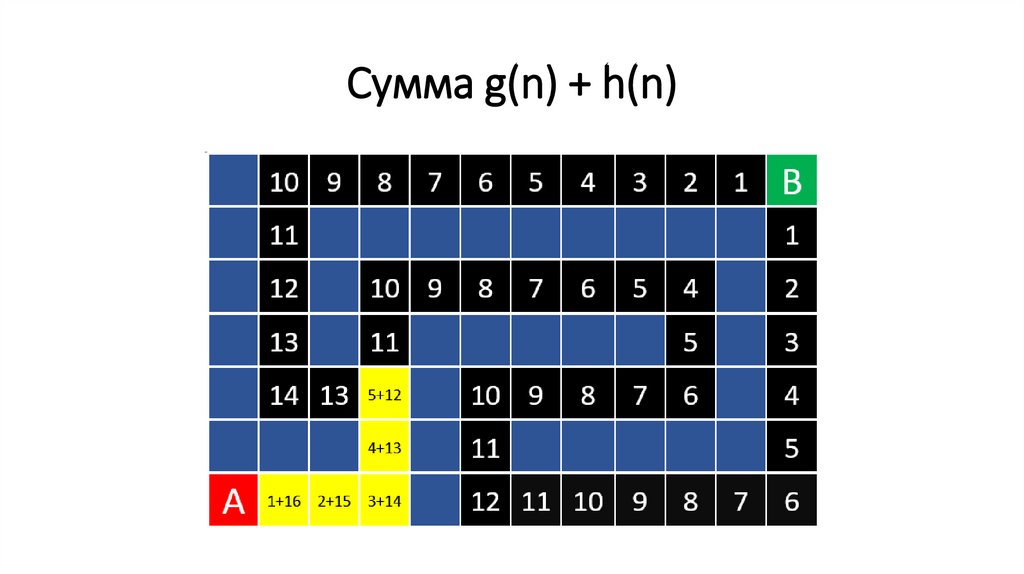
Сумма g(n) + h(n)126.
Сумма g(n) + h(n)Однако, здесь я
мог бы
находиться в
шести шагах от
начала, плюс
оценка
удаления,
равная 13. И 6 +
13 = 19 . Нужно
идти сюда!
Здесь я в 15
шагах. А оценка
удаления от
цели равняется
6. 15 + 6 = 21.
127.
Сумма g(n) + h(n)эвристические
значения на
данном пути
начинают
уменьшаться
эвристические
значения на
данном пути
начинают
увеличиваться
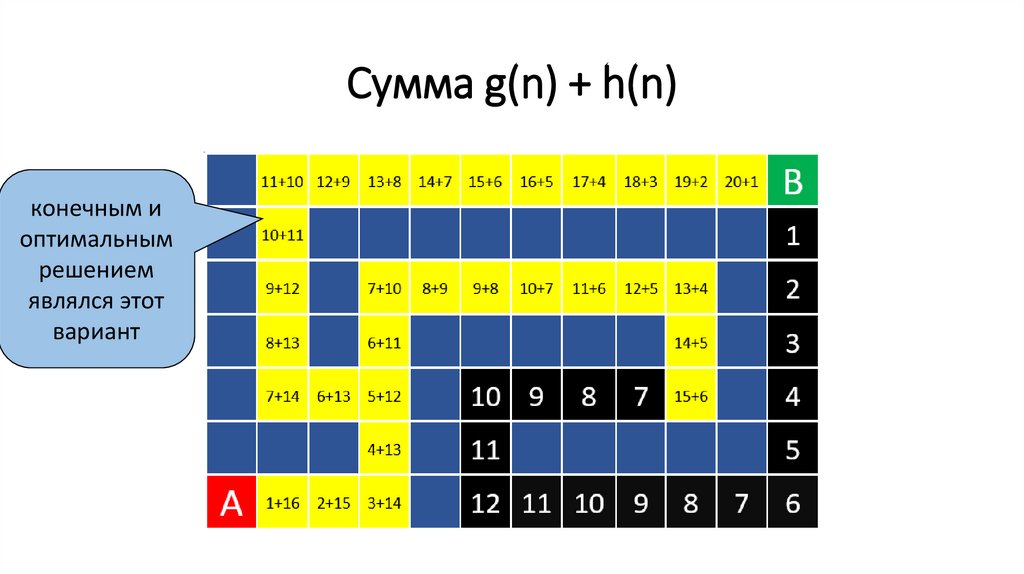
128.
Сумма g(n) + h(n)конечным и
оптимальным
решением
являлся этот
вариант
129.
Условия оптимальности применения А*• h(n) - эвристическая функция должна быть допустимой. Это
значит, что она никогда не переоценивает истинную стоимость
достижения цели.
• h(n)- эвристическая функция должна быть преемственной. Это
значит, что эвристическое значение для каждого узла (назовём
его n) и его преемника (следующего за ним узла), который мы
назовём n’ со стоимостью шага с, должно быть:
h(n)≤ h(n’) + с
130.
Условия оптимальности применения А*• Выражаясь простыми словами это значит, что если сейчас я
нахожусь здесь, то эвристическое значение от меня до цели не
должно превышать эвристическое значение моего преемника
(следующего потенциального шага) в сумме с текущей
стоимостью пути.
• Выбор эвристического значения может вызвать сложности. Чем
лучше эвристическое значение, тем лучше я решу задачу и тем
меньшее число состояний придется посетить.
131.
Множественность агентов(Adversarial Search)
• Иногда в задачах поиска мы оказываемся в состязательной
ситуации, где я являюсь агентом, который пытается принимать
умные решения, а кто-то мешает мне - у него противоположная
цель. И чаще всего такие ситуации встречаются в играх.
132.
Крестики-нолики• Как же выглядит умное решение в игре?
133.
Крестики-нолики• Но теперь крестик делает умный ход.
134.
Алгоритм Минимакс (Minimax)• Каждый раз, когда мы используем человеческие концепты такие
как «победа» и «поражение», нам надо сделать их понятными
для компьютера.
• Понятие «победы» и «поражения» не ясны компьютеру. А
«больше» и «меньше» - ясны.
• Мы можем присвоить значение или полезность каждой из
возможных ситуаций, которая может случиться в этой игре.
135.
Возможные исходы игры крестики-нолики-1
0
1
136.
Формализация цели игры• MAX (X) хотят, чтобы счёт был больше
• MIN (O) стремятся минимизировать счет
137.
Формализация игры для ИИS0 - начальное состояние (initial state)
Рlayer(s) - в качестве входных данных она будет принимать состояние,
обозначенное как s. В качестве выходных данных этой функции будет
информация о том, чей сейчас ход.
Actions(s) - представление о доступных действиях.
Result (s, a) - представление о модели перехода. Когда у меня есть
состояние и я выполняю действия, мне необходимо узнать его результат
Terminal(s) - что-то вроде проверки цели. Нам нужна проверка
терминального состояния - состояния при котором игра считается оконченной
Utility(s) - функция, которая на основе состояния определяет числовое
значение для терминального состояния как бы сообщая: если крестик
выиграет, то это равняется 1. Если выиграет нолик - это равняется -1. Если
никто не выиграет - у такого исхода значение равно 0.
138.
Начальное состояние (Initial State)139.
Функция Player(s)Player(
)=
Player(
)=
140.
Функция Actions(s)Представим, что на поле сейчас такая ситуация и
очередь ходить нолика. Что произойдет, когда мы
передадим эти сведения функции Actions(s)?
Actions (
)={
,
}
141.
Функция Result (s, a)Применив к этому состоянию функцию Result (s, a)
для ситуации, когда нолик походит в верхней левый угол,
мы получим состояние с ноликом в верхнем левом углу
Result (
,
)=
142.
Функция Terminal(s)Terminal (
) = false
Terminal (
) = true
143.
Функция Utility(s)Utility (
)=1
Utility (
) = -1
Value =1
144.
Пример игровой ситуации № 1.1.Чья очередь хода?
Player(s) = О
2. Каково значение этой ситуации на поле?
3. Как надо походить нолику?
145.
Расчеты на поле (шаг 1)Min-Value
в этой
ситуации есть
всего два
свободных
квадрата, что
означает, что у
нолика только
два варианта
для
следующего
хода.
146.
Расчеты на поле (шаг 2)Min-Value
Min-Value=0
крестик пытается найти
максимально
возможное значение
Max-Value =1
Value=1
Max-Value
Max-Value=0
Value=0
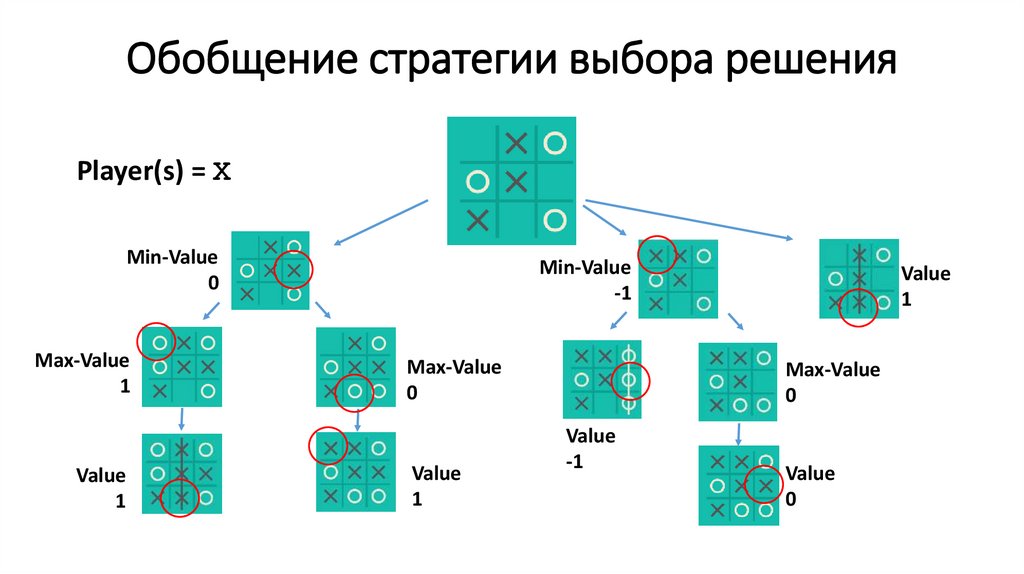
147.
Обобщение стратегии выбора решенияPlayer(s) = Х
Min-Value
0
Max-Value
1
Value
1
Min-Value
-1
Max-Value
0
Value
1
Value
1
Max-Value
0
Value
-1
Value
0
148.
Упрощение представления5
3
9
149.
Стратегия максимизирующего игрока9
5
3
9
150.
Стратегия минимизирующего игрока8
9
5
3
8
9
92
8
151.
Псевдокод для алгоритма Минимакс• Задаемся состоянием state s:
• MAX выберет действие а в функции Actions(s) , которое даёт наибольшее
значение функции Min-Value (Result (s,a))
• MIN выберет действие а в функции Actions(s) , которое даёт наименьшее
значение функции Max-Value (Result (s,a))
152.
Реализация Mах-Value (state).function Mах-Value (state):
if Terminal (state):
return Utility (state)
v = -∞
for action in Actions (state):
v = Mах(v, Min-Value (Result (state, action))):
return v
153.
Реализация Mах-Value (state).function Min-Value (state):
if Terminal (state):
return Utility (state)
v = +∞
for action in Actions (state):
v = Min(v, Max-Value (Result (state, action))):
return v
154.
Необходимость оптимизации155.
Необходимость оптимизации4
4
8
5
156.
Необходимость оптимизации3
4
4
8
5
9
3
7
157.
Необходимость оптимизации4
4
8
2
3
4
5
9
3
7
2
4
6
158.
Механизм оптимизации4
4
8
5
159.
Механизм оптимизации≤3
4
4
8
5
9
3
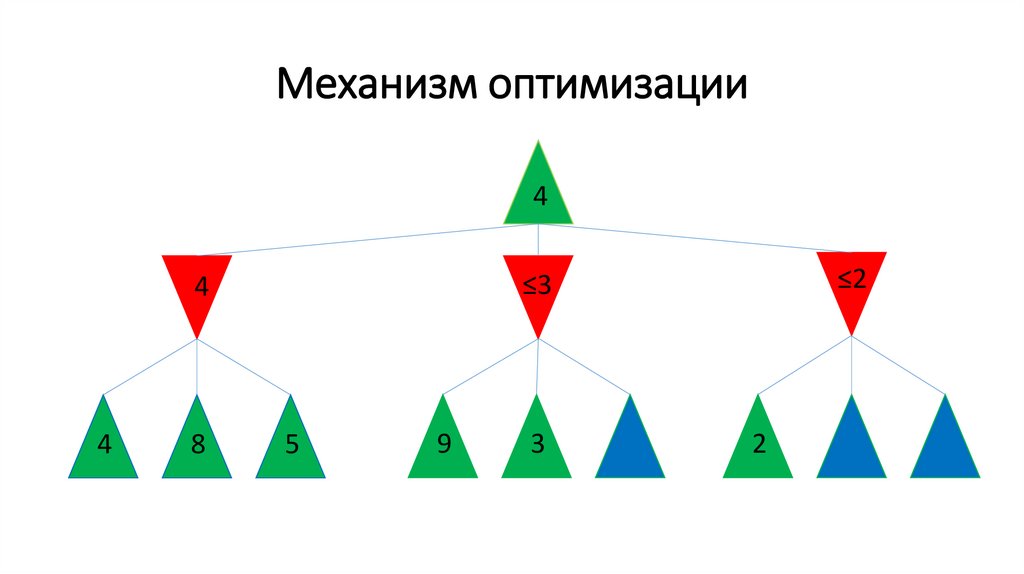
160.
Механизм оптимизации4
4
8
≤2
≤3
4
5
9
3
2
161.
α-β отсечение• α и β - это два значения, которые вы отслеживаете - наилучшее и
наихудшее действия. Идея отсечения заключается в том, чтобы
при наличии большого дерева поиска я мог выполнять поиск
более эффективно не исследуя каждый узел, а имея возможность
удалять некоторые из них, оптимизируя пространство поиска.
162.
Сложность игр255 168
288 000 000 000
29
000
10
163.
Алгоритм минимакс с ограничениемглубины (Depth-Limited Minimax)
• Минимакс с ограничением глубины прекращает поиск после
определённого количества ходов, поскольку рассчитать все
возможные варианты становятся крайне затруднительно
• Но, что происходит после того как мы попадаем в состояние где
игра не закончена?
• Минимаксу необходимо присвоить значение состоянию игрового
поля, что сложно сделать, если игра не окончена.
• функция evaluation
164.
Функция evaluationevaluation оценивает ожидаемую полезность игры в текущей
момент
Шахматы:
1 - победа белых фигур; -1 - победа чёрных фигур; 0 – ничья.
счёт 0,8
победа белых вероятнее, но не безоговорочна
165.
Итоговое резюме1. мы рассмотрели состязательный поиск, когда в игре у меня есть
соперник. Такие переборные задачи то и дело появляются при
работе с искусственным интеллектом.
2. говорили о классических переборных задачах (поиск маршрута
из одной точки в другую). Каждый раз когда ИИ оказывается в
ситуации, когда надо поступить рационально (или походить в
игре) такой тип алгоритмов может очень пригодиться.
3. мы познакомились с поиском и искусственным интеллектом. В
следующей лекции мы рассмотрим знания и то, как наш ИИ
может знать информацию, рассуждать о ней и делать выводы









































































































































 informatics
informatics








