Физические основы механики. Силы в механике (лекция 2)

1.

Физика 1 курс, 1 семестр
Лекция 2. Физические основы механики
Силы в механике
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

План лекции
Наименование раздела
Номер слайда
Введение
3
Раздел 1. Фундаментальные силы
4
1.1. Гравитационная сила
5
Принцип эквивалентности
6
1.2. Кулоновская сила
7
Раздел 2. Нефундаментальные силы
8
Предварительное замечание
9
2.1. Сила тяжести
10
2.2. Вес тела
12
2.3. Сила трения
13
2.4. Сухое и вязкое трение
16
2.5. Сила упругости
17
Сводная таблица нефундаментальных сил
18
2

3.

Введение
В предыдущей, 3-й лекции нашего курса были последовательно рассмотрены три закона Ньютона,
которые определяют основополагающие принципы движения и покоя тела (материальной точки или
системы материальных точек).
Формулирование этих законов потребовало введения нового понятия – силы, которое было
определено в самом общем виде так:
Сила – это характеристика механического воздействия на рассматриваемое тело со стороны других
тел. Сила возникает при непосредственном контакте тел (напр., при столкновении бильярдных шаров)
и при нахождении тела во внешнем поле (гравитационном, электрическом и др.), т.е. без контакта тел.
В 4-ой лекции нашего курса типичные силы в механике рассмотрены более подробно. При этом
будут выделены:
- фундаментальные силы, т.е. силы, которые нельзя свести к другим, более простым силам;
- другие, нефундаментальные силы, которые сводятся к фундаментальным; точнее,
нефундаментальные силы объясняются действием сил фундаментальных.
Важность нефундаментальных сил нельзя недооценивать!
Все силы рассматриваются в нерелятивистском приближении, когда все тела покоятся или
движутся с малой скоростью (по сравнению со скоростью света).
3

4.

Раздел 1. Фундаментальные силы
4

5.

1. Фундаментальные силы
1.1. Гравитационная сила
Сила гравитации (или сила тяготения) возникает в результате действия закона всемирного тяготения:
любые два тела, обладающие массами m1 и m2, притягиваются друг к другу с силой Fg:
- Гравитационная постоянная
|F1| = |F2| = |Fg|
Гравитационная сила всегда направлена по прямой линии,
соединяющей центры масс тел.
Гравитационные силы – всегда силы притяжения.
Гравитационных сил отталкивания не существует.
Конкретным проявлением гравитационной силы являются сила тяжести и вес тела. Они будут
рассмотрены в разделе 2 этой лекции.
5

6.

1. Фундаментальные силы
Принцип эквивалентности
Любое тело имеет две массы: инертную и гравитационную.
1). Масса тела из формулы второго закона Ньютона F = m∙a, масса характеризует инертные свойства
вещества (см. лекцию 3), такая масса называется инертной массой mин.
2). Масса тела из формулы закона всемирного тяготения (см. предыд. слайд), эта масса характеризует
гравитационные свойства вещества и поэтому называемая гравитационной массой mграв.
Экспериментально было установлено, что обе массы одного и того же тела равны друг другу:
mин = mграв.
Это равенство выполняется с очень высокой точностью (не хуже 10-12).
Поэтому силы инерции можно считать эквивалентными гравитационным силам. Следовательно,
движущаяся с ускорением система отсчёта эквивалентна некоторому гравитационному полю.
Пример: силы инерции в ускоренно движущемся лифте неотличимы от гравитационных сил,
действующих в истинном гравитационном поле. Как будто ускорение лифта создаётся гравитационным
притяжением к виртуальному телу, которое (тело) располагается внизу, когда лифт ускоряется вверх, или
располагается сверху, когда лифт ускоренно тормозится.
Пример из обычной жизни: ускоряющийся поезд метро заставляет нас крепче держаться за поручни, как будто
позади поезда появилось виртуальное массивное тело, притягивающее нас. В реальности, это, конечно, ускорение,
созданное электродвигателем поезда. Но воздействие обеих причин одинаково, т.е. оба физических явления
эквивалентны!
6

7.

1. Фундаментальные силы
1.2. Кулоновская сила
Кулоновская сила возникает в результате действия закона взаимодействия электрических зарядов друг
с другом (закона Кулона):
k – коэффициент пропорциональности
|F21| = |F12| = |Fk|
Сила Кулона направлена по прямой, соединяющей заряды.
Конкретным проявлением кулоновской силы являются сила упругости и сила трения. Эти силы
определяются взаимодействием молекул и атомов вещества, которое имеет электрическую, точнее,
электромагнитную природу. Они будут рассмотрены в разделе 2 этой лекции.
Кулоновская сила, как и гравитационная сила, являются фундаментальными силами, вытекающими из
самых общих законов природы: закона гравитационного взаимодействия масс и закона взаимодействия
электрических зарядов.
7

8.

Раздел 2. Нефундаментальные силы
8

9.

2. Нефундаментальные силы
Предварительное замечание
Из огромного множества сил, действующих на материальную точку (тело) в механике
принято выделять несколько основных сил, наиболее часто встречающихся в задачах.
Конкретная сила
(нефундаментальная)
Соответствующая
фундаментальная сила
Сила тяжести
Гравитационная сила
Вес тела
Сила упругости
Кулоновская сила
Сила трения
Все указанные конкретные силы являются приближёнными, они могут, в принципе,
быть получены из соответствующих фундаментальных сил. Но это резко усложнит решение
практических задач. Поэтому следует использовать конкретные силы, к рассмотрению
которых мы переходим.
9

10.

2. Нефундаментальные силы
2.1. Сила тяжести
Сила тяжести – частный случай силы гравитации. Сила тяжести возникает в результате
притяжения тела с массой m к Земле, т.е. к телу с массой Земли М:
FТ =
где R – радиус Земли
С другой стороны, для тела массой m, на которое действует сила FТ , справедлив 2закон Ньютона:
FТ = m∙a,
где а – ускорение движения.
Сравнивая обе формулы для FT, получим формулу для величины ускорения: а
.
Таким образом, величина ускорения тела массой m в поле тяготения Земли определяется только
постоянными величинами (гравитационной постоянной, массой и радиусом Земли). Значит, ускорение
в поле тяжести Земли также является постоянной величиной, которая имеет свои обозначение (g) и
название – ускорение свободного падения.
Подставив в эту формулу табличные значения гравитационной постоянной G, массы и радиуса
Земли, получим значение g = 9,81 м/с2. Обратите внимание: три значащие цифры.
Сила тяжести традиционно записывается так: FT = m∙g.
10

11.

2. Нефундаментальные силы
2.1. Сила тяжести (продолжение)
Очевидно, что на высоте h над уровнем Земли сила тяготения рассчитывается несколько иначе:
Значит, ускорение свободного падения также будет несколько другим. Напишите формулу для g(h).
Строго говоря, полученное на предыдущем слайде значение g = 9,81 м/с2, действует только на
поверхности Земли (h=0). Но опыт расчётов показывает, что это значение g можно использовать с
приемлемой точностью до общепринятой границы космоса: h=100 км.
Самостоятельно: определите отличие в значениях ускорения свободного падения на уровне Земли и на границе космоса.
11

12.

2. Нефундаментальные силы
2.2. Вес тела
Вес тела – сила, с которой тело вследствие притяжения к Земле действует на опору или
растягивает подвес.
Для определения веса опора должна быть строго горизонтальной, подвес должен быть строго
вертикальным.
Количественно вес тела Р равен силе тяжести Fтяж : Р = Fтяж = m∙g.
Это равенство справедливо и по модулю, и по направлению.
N
Отличие веса тела от силы тяжести состоит в точке приложения этих сил:
- вектор силы тяжести ВСЕГДА приложен к центру масс тела.
- вектор веса тела ВСЕГДА приложен к точке соприкосновения тела с
опорой или к точке закрепления подвеса.
Чёрной стрелкой показан вектор силы реакции опоры N.
|N| = |Fтяж| = |P|
В случае материальной точки все три вектора будут приложены к самой этой точке, при этом
вектор силы тяжести будет совпадать с вектором веса тела.
Нарисуйте векторы силы тяжести Fтяж, веса тела Р, силы реакции точки подвеса и натяжения нити когда тело подвешено.12

13.

2. Нефундаментальные силы
2.3. Сила трения
Сила трения – это сила, препятствующая движению тела или возникновению движения.
Сила трения покоя – это сила, возникающая когда тела первоначально неподвижны
Пианино не удастся
относительно друг друга.
сдвинуть с места до тех
Сила трения покоя препятствует страгиванию тела с места:
пор, пока усилия человека
не станут достаточными:
неподвижное тело не двигается с места до тех пор, пока
F > Fтр.пок
приложенная сила не превысит некоторое значение.
(Непонятно, зачем этот человек
Это пороговое значение называется силой трения покоя.
двигает пианино боком?!)
Сила трения скольжения – это сила, возникающая при движении тел друг относительно друга.
В этом случае одно тело скользит по поверхности соприкосновения с другим телом,
без вращения (см. рис. справа).
Важно: Здесь и далее точка приложения силы трения помещена в точку центра масс;
в реальности сила трения возникает в плоскости контакта тел.
Главное условие, при котором одно тело может скользить
относительно другого – приложенная к телу внешняя сила
должна быть больше силы трения скольжения: Fвнешн > Fтр
(см. рис. справа внизу).
13

14.

2. Нефундаментальные силы
2.3. Сила трения (продолжение)
Экспериментально установлено, что сила трения скольжения (или просто: сила трения) Fтр
пропорциональна силе реакции опоры одного тела на поверхность другого N с коэффициентом
пропорциональности μ (читается: «мю»); другое название коэффициента μ – коэффициент трения.
Fтр = μ∙N.
Коэффициент μ – табличная величина, её значение определяется парой контактирующих материалов.
Сила реакции опоры N всегда перпендикулярна к поверхности опоры и зависит от геометрии задачи.
При движении по горизонтальной поверхности:
N = m∙g.
Тогда Fтр = μ∙m∙g.
При движении по наклонной плоскости:
N = m∙g∙cosα.
Тогда Fтр = μ∙m∙g∙cosα.
Обратите внимание: на рисунках все силы приложены
к центру масс тела. Это означает, что тело рассматривается
как материальная точка.
14

15.

2. Нефундаментальные силы
2.3. Сила трения (продолжение)
Полезный вывод из ситуации со скольжением по наклонной
плоскости.
Все действующие силы и их разложение по осям показаны
на рисунке справа.
Интуитивно и из опыта ясно, что при малых значениях угла
α тело не будет скатываться, т.к. скатывающая сила будет меньше
силы трения:
mg∙sin(α) < μ∙mg∙cos(α)
По мере увеличения угла α наступит момент, когда тело
начнёт скольжение по наклонной плоскости. Угол наклона
плоскости при этом составит α0.
Тогда значение коэффициента трения μ составит:
μ = tgα0.
Попробуйте самостоятельно это доказать.
Именно эти простые соображения легли в основу
распространённого метода определения коэффициента трения
для многих пар контактирующих материалов.
Внимание! Используется обозначение скорости
курсивом (v), рисунок взят из интернета.
15

16.

2. Нефундаментальные силы
2.4. Сухое и вязкое трение
Сухое трение возникает между поверхностями твёрдых тел в отсутствии смазки.
Fсух.тр = μ∙N
Коэффициент трения μ – табличная величина, её значение определяется парой контактирующих материалов.
Вязкое (жидкое) трение – это трение между твёрдым телом и жидкой или
газообразной средой, в которой тело движется. Характерный пример вязкого трения
– это трение, возникающее при движении твёрдого шарика в жидкости или газе. Такое
движение сопровождается очень сложным движения самой жидкой или газообразной
среды, что вносит значительный вклад в сопротивление среды, т.е. в величину вязкого
трения.
Упрощенно можно считать, что сила вязкого трения:
Fвяз.тр. = k1∙v при малых скоростях движения твёрдого тела в жидкости или в газе;
Fвяз.тр. = k2∙v2 при больших скоростях движения.
Дополнение: Сила вязкого трения, возникающая при таком движении, называется силой Стокса.
Fвяз.тр = FСтокс = 6π∙η∙r∙v
(на рисунке эта сила обозначена как FТР)
η – коэффициент вязкости среды, табличная величина
r – радиус шарика
v – скорость движения шарика
Самостоятельно: Известно, что через некоторое время скорость
падения шарика в жидкости станет постоянной. Определите эту
16
скорость vСтокс и рассчитайте её значение при падении шарика в воде.

17.

2. Нефундаментальные силы
2.5. Сила упругости
Сила упругости возникает при сжатии или растяжении упругого (или абсолютно упругого) тела.
Сила упругости пропорциональна величине деформации (растяжения или сжатия) и направлена в
противоположную сторону от внешней силы, вызывающей эту деформацию.
Fупр = - k∙x
– закон Гука
х – величина деформации, изменение длины пружины,
часто используется другое обозначение деформации: ∆х;
k – коэффициент упругости или жёсткости - для пружин;
значение k определяется свойствами материала
(пружины) и является справочной величиной.
Сила упругости всегда стремится уменьшить величину деформации и вернуть тело в исходное
положение, т.е. в положение х = 0 (или ∆х = 0).
Важно: понятие упругого или абсолютно упругого тела означает, что после прекращения действия
17
внешней силы (например, силы растяжения) тело принимает первоначальные форму и размеры.

18.

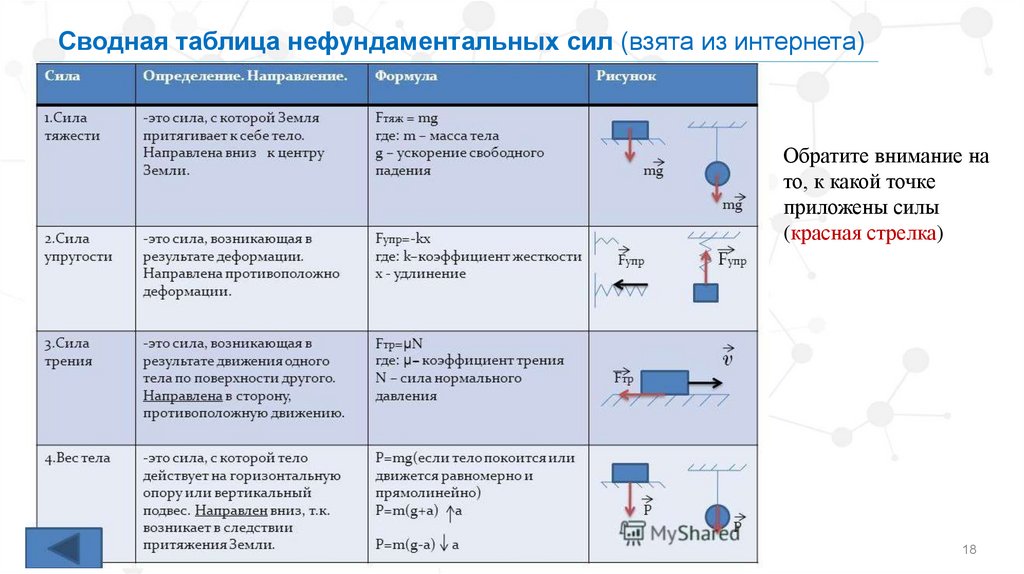
Сводная таблица нефундаментальных сил (взята из интернета)
Обратите внимание на
то, к какой точке
приложены силы
(красная стрелка)
18

19.

Спасибо за внимание