Параллельность прямых и плоскостей в пространстве

1.

«Параллельность
прямых и плоскостей
в пространстве»

2.

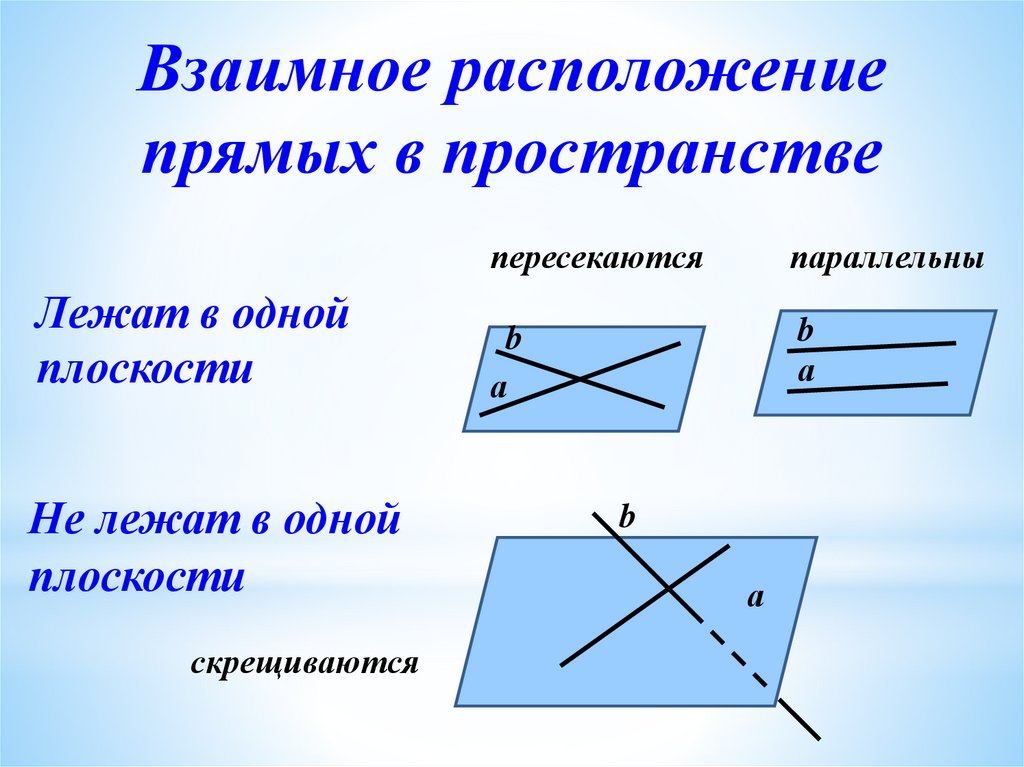
Взаимное расположение
прямых в пространстве
Лежат в одной
плоскости
Не лежат в одной
плоскости
скрещиваются
пересекаются
параллельны
b
а
b
а
b
а

3.

в
в1
а
β
α
•В
с
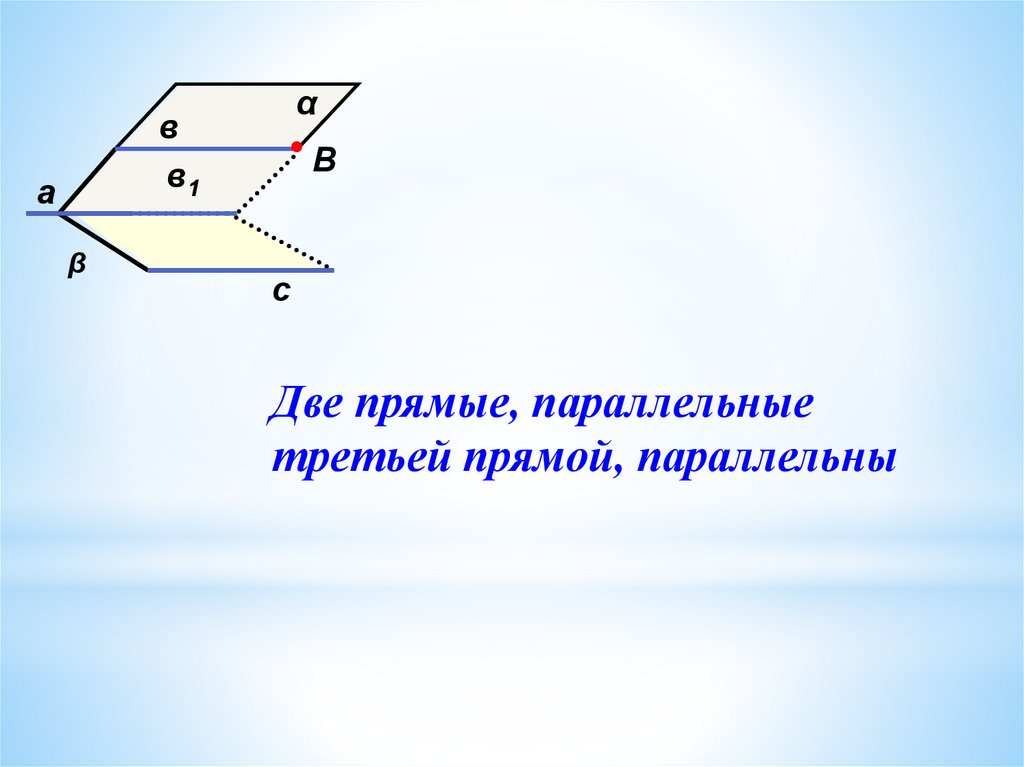
Две прямые, параллельные
третьей прямой, параллельны

4.

a
К
b
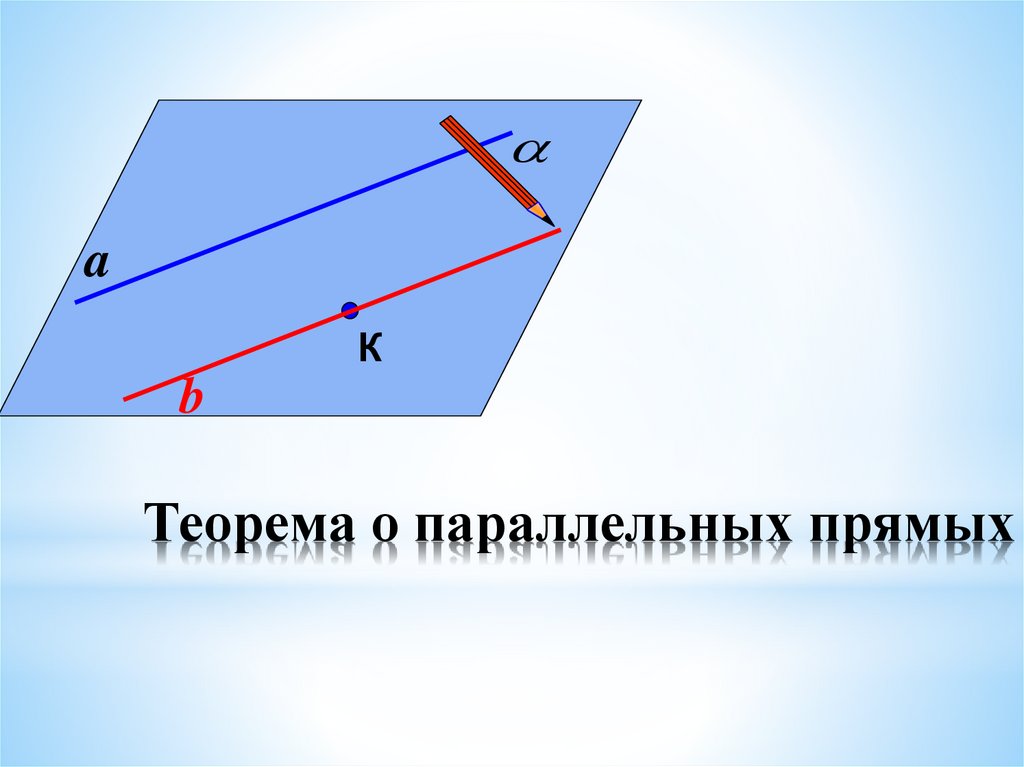
Теорема о параллельных прямых

5.

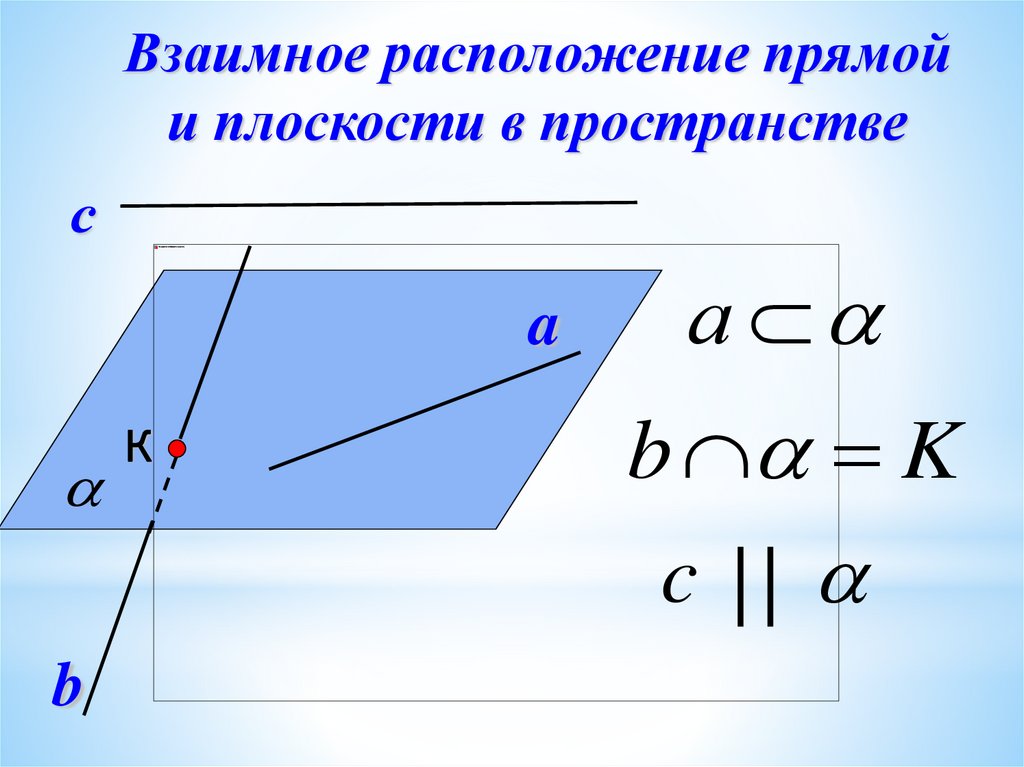
Взаимное расположение прямой
и плоскости в пространстве
a
b
К
а
b K
c

6.

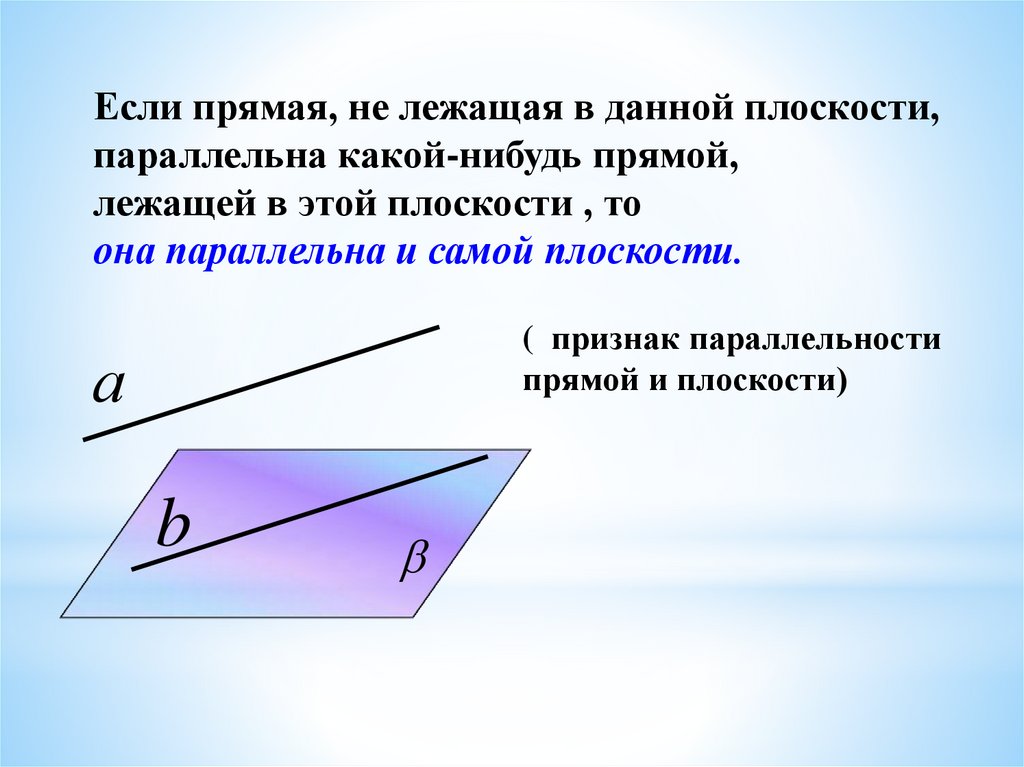
Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой,
лежащей в этой плоскости , то
она параллельна и самой плоскости.
( признак параллельности
прямой и плоскости)
а
b

7.

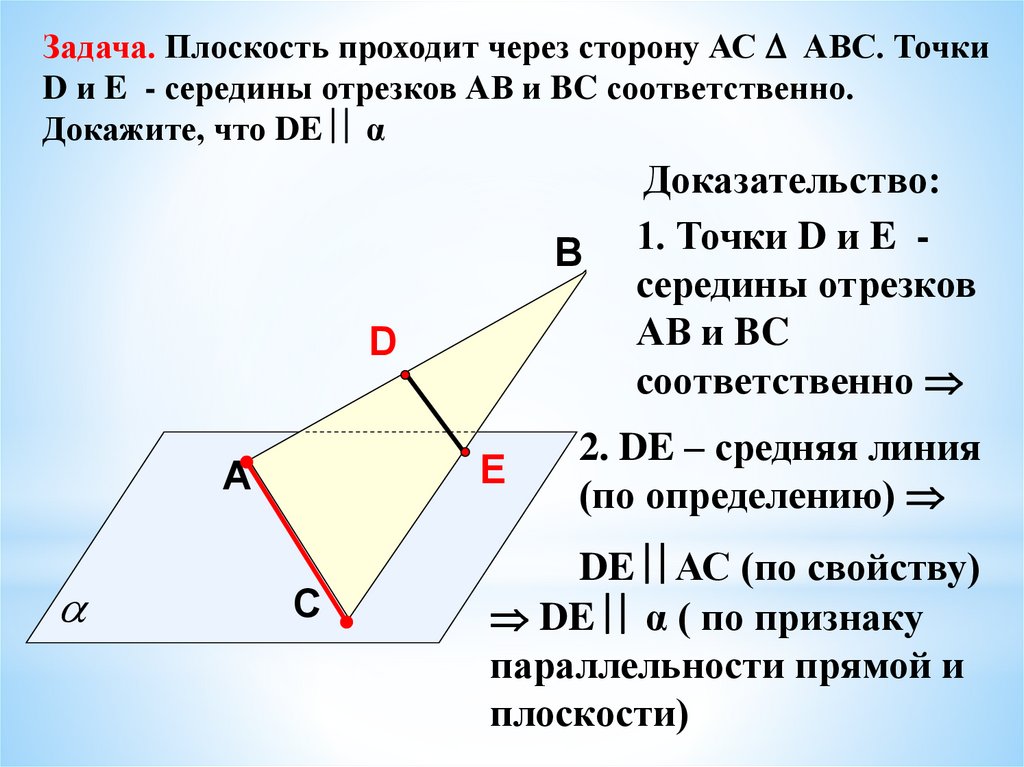
Задача. Плоскость проходит через сторону АС АВС. Точки
D и E - середины отрезков АВ и BC соответственно.
Докажите, что DE α
В
D
E
A
С
Доказательство:
1. Точки D и E середины отрезков
АВ и BC
соответственно
2. DE – средняя линия
(по определению)
DE АС (по свойству)
DE α ( по признаку
параллельности прямой и
плоскости)

8.

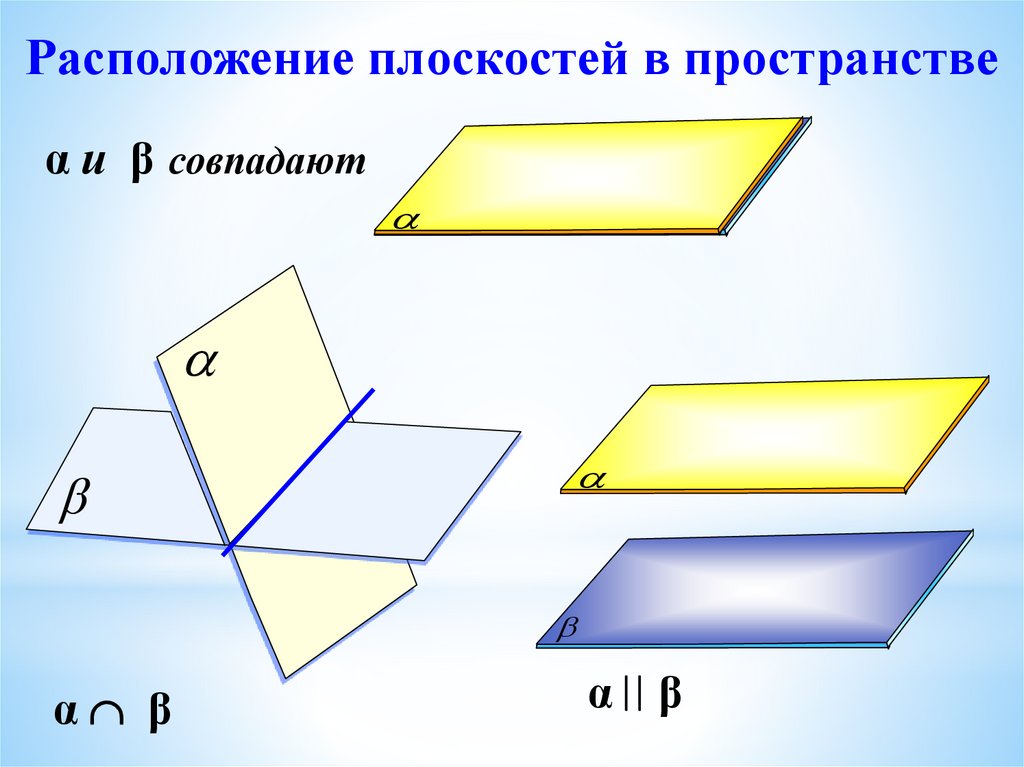
Расположение плоскостей в пространстве
α и β совпадают
α β
α β

9.

Признак параллельности двух плоскостей
а
b
а₁
b₁
Если две пересекающиеся
прямые одной
плоскости
соответственно
параллельны двум
пересекающимся прямым
другой плоскости,
то эти плоскости
параллельны.

10.

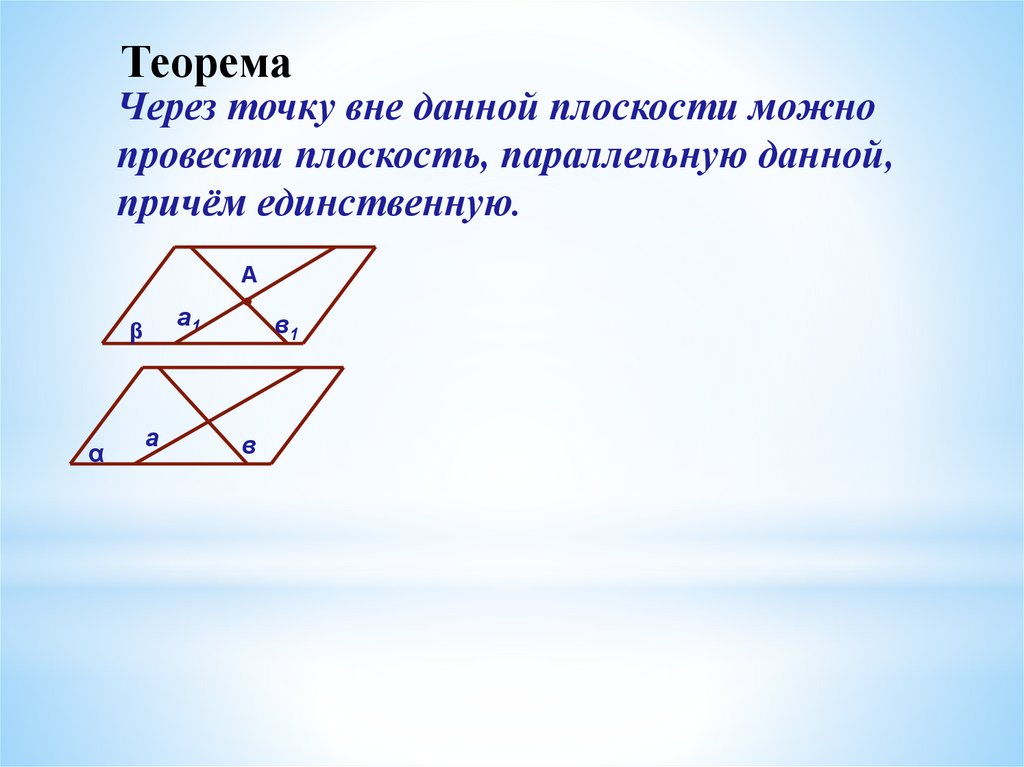
Теорема
Через точку вне данной плоскости можно
провести плоскость, параллельную данной,
причём единственную.
А
а1
β
α
а
в
в1

11.

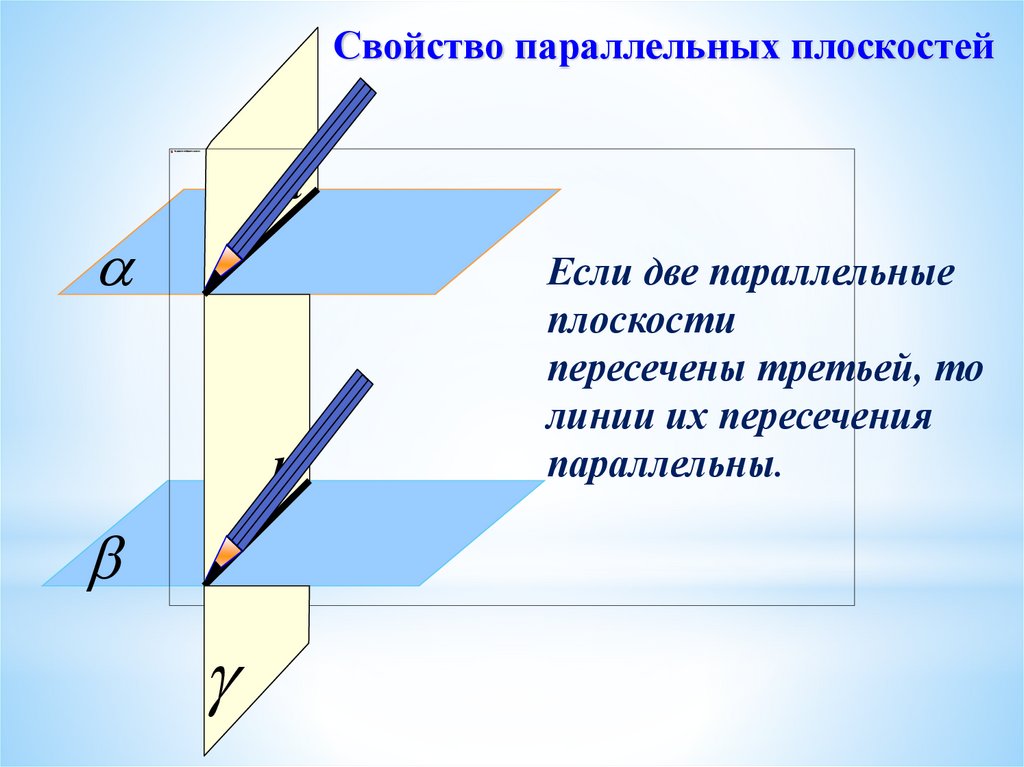
Свойство параллельных плоскостей
а
b
Если две параллельные
плоскости
пересечены третьей, то
линии их пересечения
параллельны.

12.

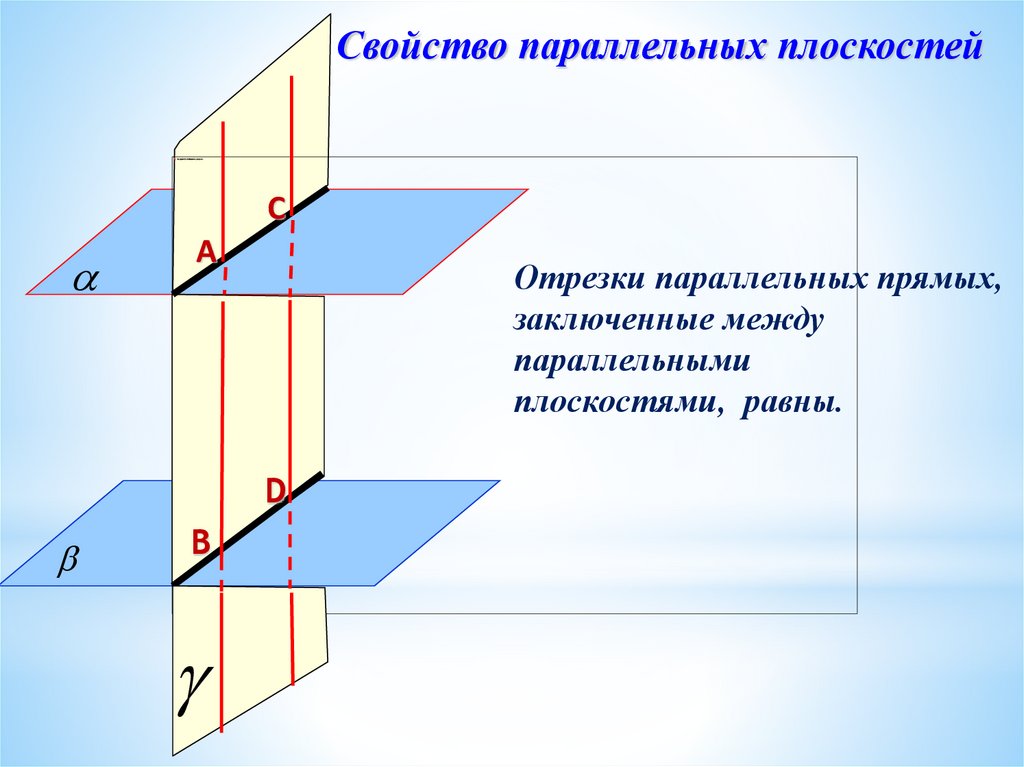
Свойство параллельных плоскостей
С
А
Отрезки параллельных прямых,
заключенные между
параллельными
плоскостями, равны.
D
В

13.

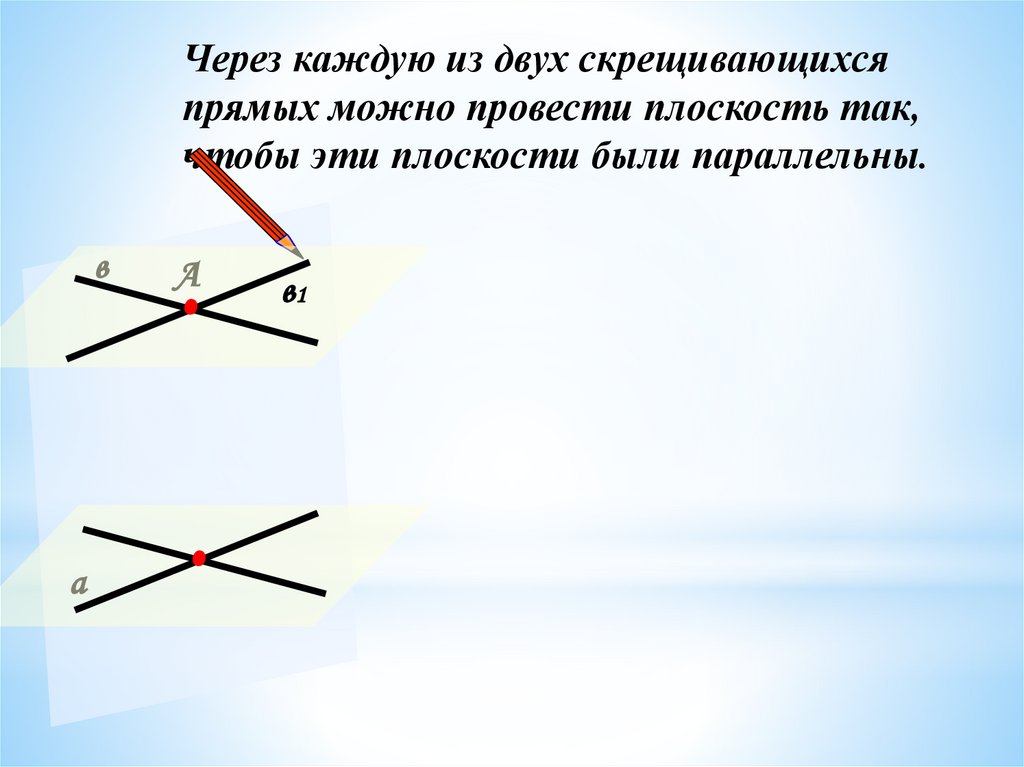
Через каждую из двух скрещивающихся
прямых можно провести плоскость так,
чтобы эти плоскости были параллельны.
в
а
.
А
.
в1