Биология березова диана 321 г

1.

Тема:Методы моделирования в био экологии:создание
математических прогнозирование изменений
КГБПОУ. «Бийский техникум лесного хозяйства»
Березова Диана
321группа

2.

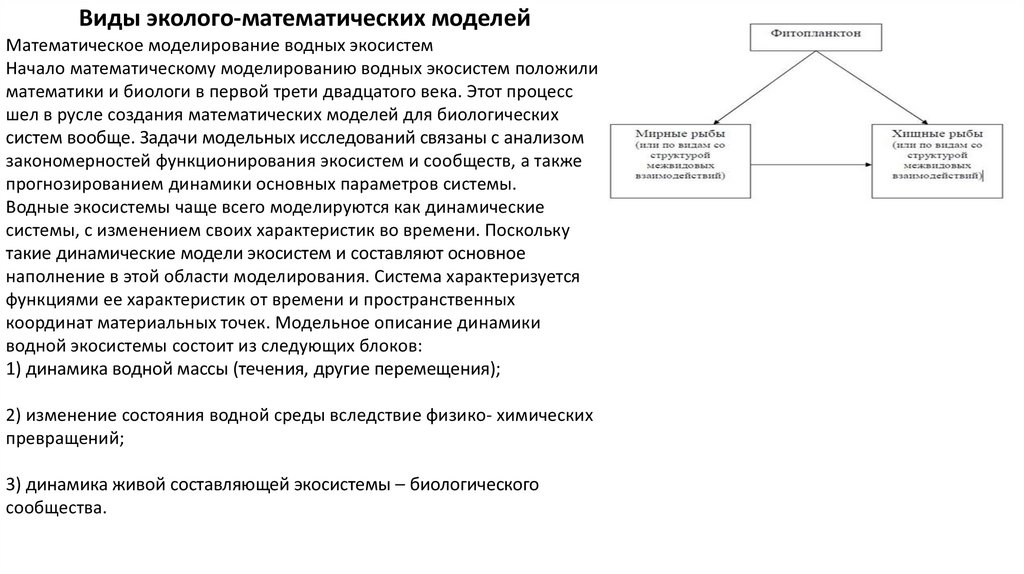
Виды эколого-математических моделей
Математическое моделирование водных экосистем
Начало математическому моделированию водных экосистем положили
математики и биологи в первой трети двадцатого века. Этот процесс
шел в русле создания математических моделей для биологических
систем вообще. Задачи модельных исследований связаны с анализом
закономерностей функционирования экосистем и сообществ, а также
прогнозированием динамики основных параметров системы.
Водные экосистемы чаще всего моделируются как динамические
системы, с изменением своих характеристик во времени. Поскольку
такие динамические модели экосистем и составляют основное
наполнение в этой области моделирования. Система характеризуется
функциями ее характеристик от времени и пространственных
координат материальных точек. Модельное описание динамики
водной экосистемы состоит из следующих блоков:
1) динамика водной массы (течения, другие перемещения);
2) изменение состояния водной среды вследствие физико- химических
превращений;
3) динамика живой составляющей экосистемы – биологического
сообщества.

3.

Обсуждаемое здесь моделирование связано с живыми компонентами экосистемы. Неживые компоненты
рассматриваются постольку, поскольку это необходимо для моделирования динамики основных параметров живых
компонент. В свете этого цели математического моделирования водных экосистем могут быть следующими:
1) анализ качества биологической информации и данных о среде обитания;
2) анализ схемы и баланса основных потоков вещества (энергии) в экосистеме;
3) анализ последствий тех или иных воздействий на экосистему;
4) прогноз динамики основных характеристик экосистемы.
Основу функционирования экосистемы составляют нижние трофические уровни: планктон, бактерии, простейшие. От
этих блоков зависят скорости и объемы потоков вещества или энергии в системе. Модели фитопланктонных и
микробиологических сообществ чаще всего основаны на системах дифференциальных уравнений. Изучение и
моделирование первичной продукции является предметом многочисленных исследований. Выработана концепция
лимитирующих факторов и способы ее математической формализации.
Традиционный путь изучения сообществ микроорганизмов заключается в моделировании непрерывных культур.
Скорость размножения может зависеть от концентрации клеток, концентрации субстрата, температуры, pH среды и
прочих факторов.
При моделировании динамики фитопланктона, важную роли играет учет влияния уровня освещенности на скорость роста
организмов

4.

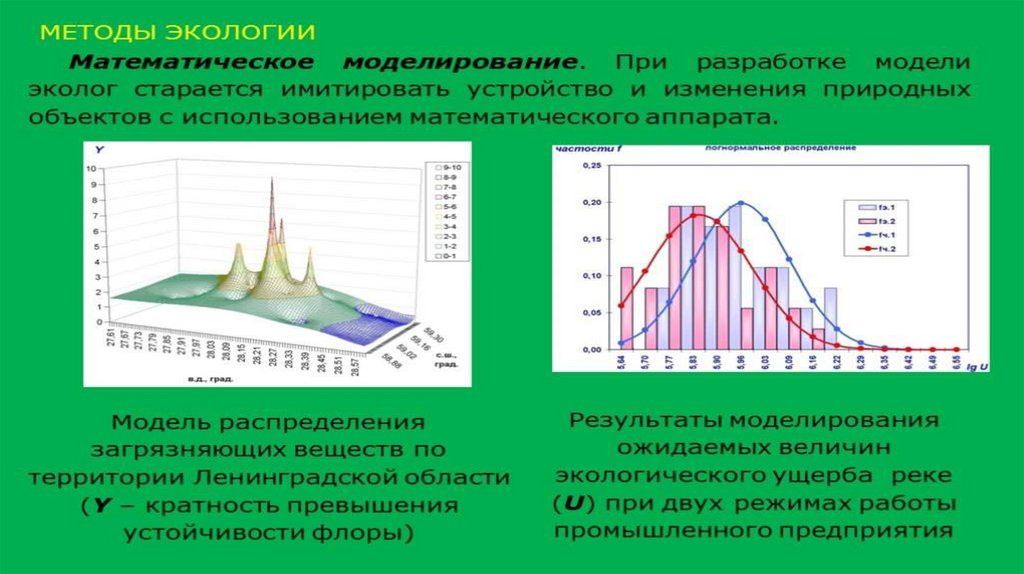
Моделирование почвенно-растительных систем
Химические вещества, выбрасываемые в окружающую среду, в конце концов, аккумулируются в почве. При этом почва
выступает не только в качестве мощного аккумулятора загрязняющих веществ, особенно тех, которые медленно
разрушаются в естественных условиях, и исходного звена в миграции токсикантов по наземным трофическим цепочкам,
но и обладает, в отличие от других природных сред, трансформирующими свойствами по отношению ко многим классам
загрязнителей.
Почвенная оболочка биосферы – педосфера – один из основных компонентов в природе, где происходит локализация
химических элементов, сбрасываемых в окружающую среду вследствие его техногенной деятельности. Возможно также
поступление в почву химических веществ и после их сброса в гидрографическую сеть с паводковыми водами, при
орошении и т.п. Почва обладает исключительно большей емкостью поглощения техногенных примесей, и интенсивная их
сорбция в почвах обеспечивает создание в наземной среде мощного слоя загрязнений. [10]
Значительную роль в изучении фитоценоза играет математическое моделирование. Создание математических моделей
фитоценозов позволяет объединить знания в области физиологии растений, биофизике, почвоведении, метеорологии с
тем, чтобы изучить функционирование фитоценозов различных степных ландшафтов.

5.

Основные цели создание моделей биогеоценозов
количественная оценка потенциального урожая различных видов растительности, произрастающих в различных
агроклиматических условиях;
прогнозирование новых параметров сортов растительности обеспечивающих максимальную продуктивность при
имеющихся условиях окружающей среды;разработка критериев оценки воздействия окружающей среды на
растительность различных агроландшафтов.Уже давно развивается идея, что для выживания организмов наиболее
важное значение имеет их высокая энергетическая мощность. Самые большие шансы для выживания у таких
организмов, которые могут использовать максимальное количество энергии в единицу времени. Это даст организму
большие возможности для поддержания и повышения организованности структур и функций. Такое свойство устойчивого
неравновесного состояния живых организмов характеризуется тем, что свободная энергия их не соответствует минимуму.

6.

МОДЕЛИРОВАНИЕ КАК МЕТОД ПОЗНАНИЯ.
.
Моделирование – это метод познания, состоящий в создании и исследовании моделей. Человечество в своей
деятельности (научной, образовательной, технологической, художественной) постоянно создает и использует модели
окружающего мира. Строгие правила построения моделей сформулировать невозможно, однако человечество накопило
богатый опыт моделирования различных объектов и процес Модели позволяют представить в наглядной форме
объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты,
очень быстрые или очень медленные процессы и др.). Наглядные модели часто используются в процессе обучения. В
курсе географии первые представления о нашей планете Земля мы получаем, изучая ее модель – глобус, в курсе физики
изучаем работу двигателя внутреннего сгорания по его модели, в химии при изучении строения вещества используем
модели молекул и кристаллических решеток, в биологии изучаем строение человека по анатомическим муляжам и др.
Математическое моделирование — процесс построения и изучения математических моделей. Все естественные и
общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием:
заменяют реальный объект его моделью и затем изучают последнюю. Математическая модель — это модель, созданная
с помощью математических понятий.

7.

8.

9.

Примеры методов исследования

10.

11.

История развития моделирования
Исторически первыми моделями как заместителями некоторых объектов были,
несомненно, символические условные модели. Ими являлись языковые знаки, естественно
возникшие в ходе развития человечества и постепенно составившие разговорный
язык.Следующим этапом развития моделирования можно считать возникновение знаковых
числовых обозначений. Сведения о результатах счета первоначально сохранился в виде
зарубок. Постепенное совершенствование этого метода привело к изображению чисел в
виде цифр как системы знаков. Можно предположить, что именно зарубки были
прототипом римских цифр I, II, III, V, X.Дальнейшее развитие знаковых моделей связано с
возникновением письменности и математической символики. Наиболее древние
письменные тексты, известные в настоящее время, относят примерно к 2000 г. до н.
э.(Египет и Вавилон). Есть основания полагать, что вавилоняне уже пользовались понятием
подобия прямоугольных треугольников.Значительное развитие моделирование получает в
древней Греции в V-III вв. до н. э. Была создана геометрическая модель Солнечной системы,
врач Гиппократ для изучения человеческого глаза воспользовался его физической
аналогичной моделью - глазом быка, математик Евклид создал учение о геометрическом
подобии.

12.

Философский аспект моделирования как способа познания
Слово "модель" произошло от латинского слова "modelium", означает:
мера, способ и т.д. Его первоначальное значение было связано со
строительным искусством, и почти во всех европейских языках оно
употреблялось для обозначения образа или вещи, сходной в каком-то отношении с другой вещью". Под моделью в
широком смысле понимают мысленно или практически созданную структуру, воспроизводящую часть действительности
в упрощенной и наглядной форме. Таковы, в частности, представления Анаксимандра о Земле как плоском цилиндре,
вокруг которого вращаются наполненные огнем полые трубки с отверстиями. Модель в этом смысле выступает как
некоторая идеализация, упрощение действительности, хотя сам характер и степень упрощения, вносимые моделью,
могут со временем меняться. В более узком смысле термин "модель" применяют тогда, когда хотят изобразить
некоторую область явлений с помощью другой, более изученной, легче понимаемой. Во многих дискуссиях,
посвященных гносеологической роли и методологическому значению моделирования, этот термин употреблялся как
синоним познания, теории, гипотезы и т.п.

13.

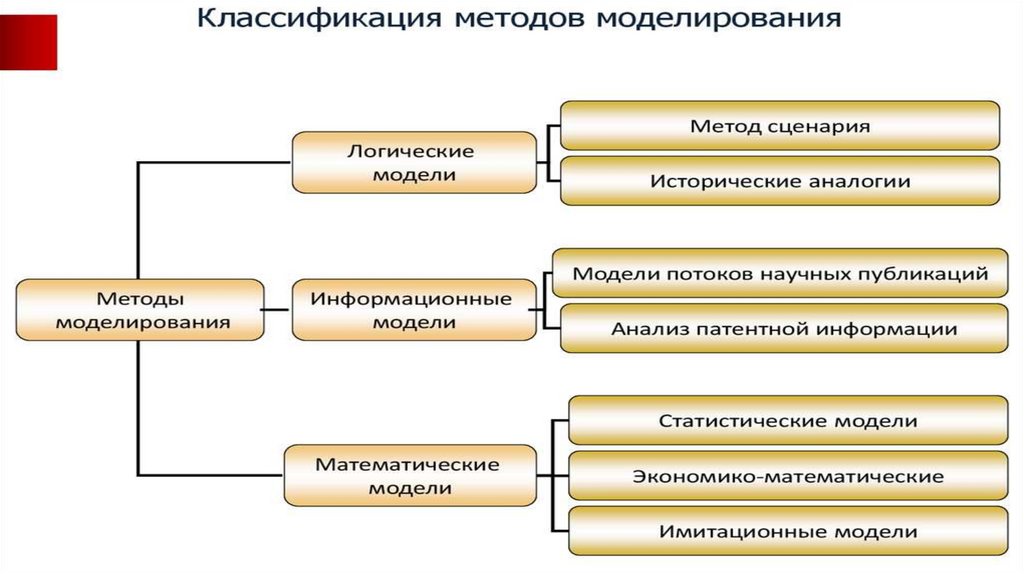
Формы представления моделей
Все модели можно разбить на два больших класса: модели предметные (материальные) и модели информационные.
Предметные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме
(глобус, анатомические муляжи). Информационные модели представляют объекты и процессы в образной или знаковой
форме.
Образные модели (рисунки, фотографии) представляют собой зрительные образы объектов, зафиксированные на какомлибо носителе информации (бумаге, кинопленке). Широко используются образные информационные модели в
образовании (плакаты по различным предметам) и науках, где требуется классифицировать объекты по их внешним
признакам.
Модели классифицируются по временному фактору:
Статическая модель — это как бы одномоментный срез информации по объекту. Например, обследование учащихся в
стоматологической поликлинике дает картину состояния их ротовой полости на данный момент времени: число
молочных и постоянных зубов, пломб, дефектов и т.п.
Динамическая модель позволяет увидеть изменения объекта во времени. В примере с поликлиникой карточку
школьника, отражающую изменения, происходящие с его зубами за многие годы, можно считать динамической моделью

14.

Список источников литературы
1.информация:https://nsportal.ru/shkola/algebra/library/2012/04/11/issledovatels
kaya-rabota-na-temu-matematicheskoe-modelirovanie-v
2.научные исследования:https://infourok.ru/matematicheskoe-modelirovanieekologicheskih-processov-2739921.html
3.История развития
моделирования:https://studfile.net/preview/4644294/page:2/
4.научные определения:https://studfile.net/preview/4644294/page:4/