Similar presentations:
Удаление путем сдвига
1.
Удаление путем сдвигаЗадача 1. Удалить из массива A[1:k] все элементы,
удовлетворяющие условию B<A[i]≤L, i=1,k путем сдвига,
т.е. без формирования нового массива.
Постановка задачи
Дано: k-цел, A[1:k]-вещ, B-вещ, L-вещ
Результат: n-цел, A[1:n] -вещ или сообщение «нет удаления»
или сообщение «полное удаление»
При : kЄN, k≤lmax, B<L
Связь:
∀ i=1,k : B≥A[i] или A[i] >L Ǝ j=1,n :A[j]=A[i].
2.
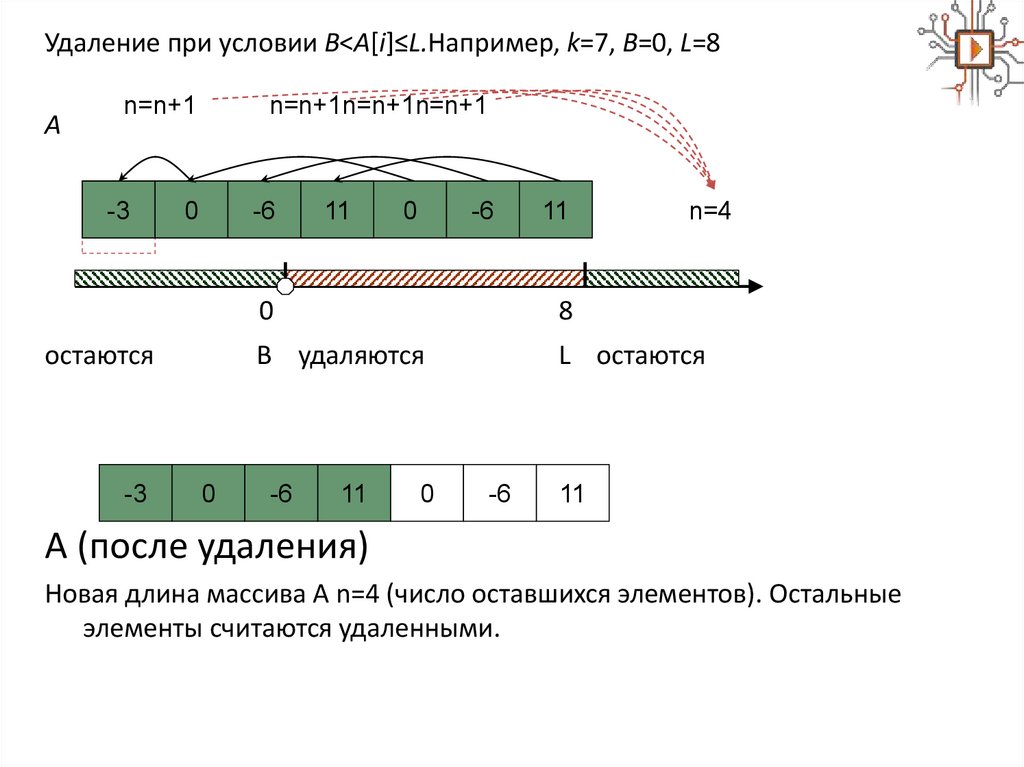
Удаление при условии B<A[i]≤L.Например, k=7, B=0, L=8A
n=n+1
n=n+1n=n+1n=n+1
-3
2
-6
8
-3
0
остаются
-3
0
11
4
0
-6
11
n=4
n=3
n=2
n=1
n=0
0
8
B удаляются
L остаются
-6
11
0
-6
11
A (после удаления)
Новая длина массива A n=4 (число оставшихся элементов). Остальные
элементы считаются удаленными.
3.
Для отрицания условий, содержащих неравенства, используютсязаконы де Моргана.
1. не (A и B) = не (A) или не (B)
2. не (A или B) = не (A) и не (B)
Удаление происходит при условии:
B<A[i]≤L, т.е. B<A[i] и A[i]≤L
Элемент остается, если не(B<A[i] и A[i]≤L). По первому закону
де Моргана получим:
не(B<A[i] и A[i]≤L)
=
не(B<A[i] ) или не( A[i]≤L)
=
B≥A[i] или A[i]>L.
4.
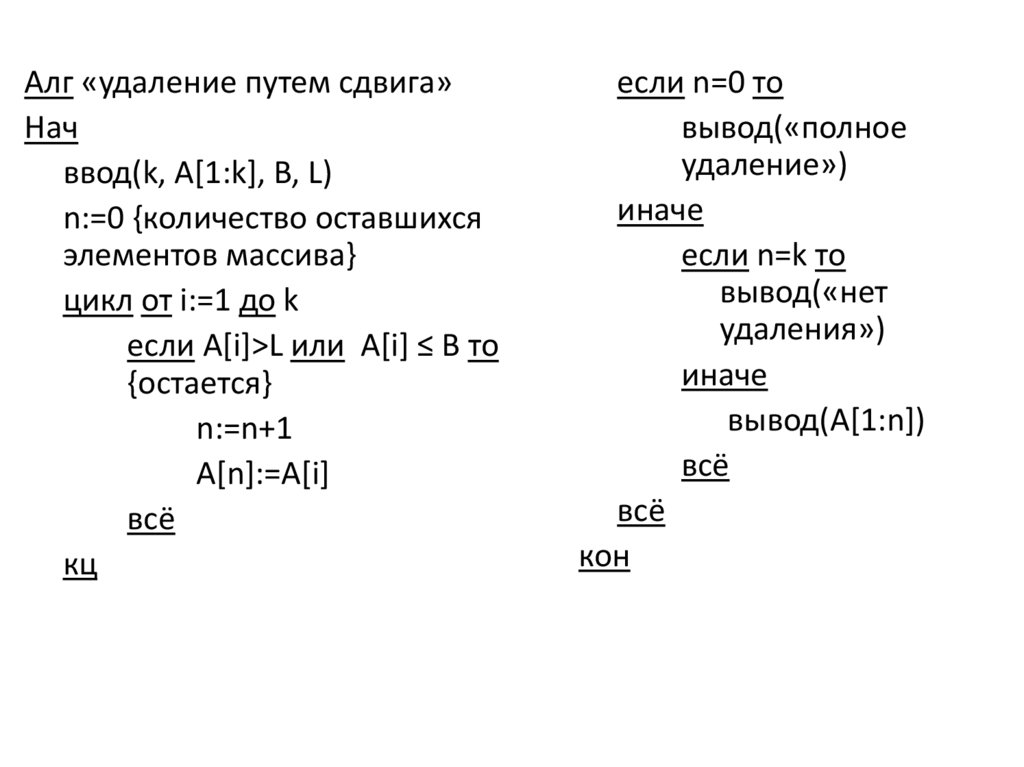
Алг «удаление путем сдвига»Нач
ввод(k, A[1:k], B, L)
n:=0 {количество оставшихся
элементов массива}
цикл от i:=1 до k
если A[i]>L или A[i] ≤ B то
{остается}
n:=n+1
A[n]:=A[i]
всё
кц
если n=0 то
вывод(«полное
удаление»)
иначе
если n=k то
вывод(«нет
удаления»)
иначе
вывод(A[1:n])
всё
всё
кон
5.
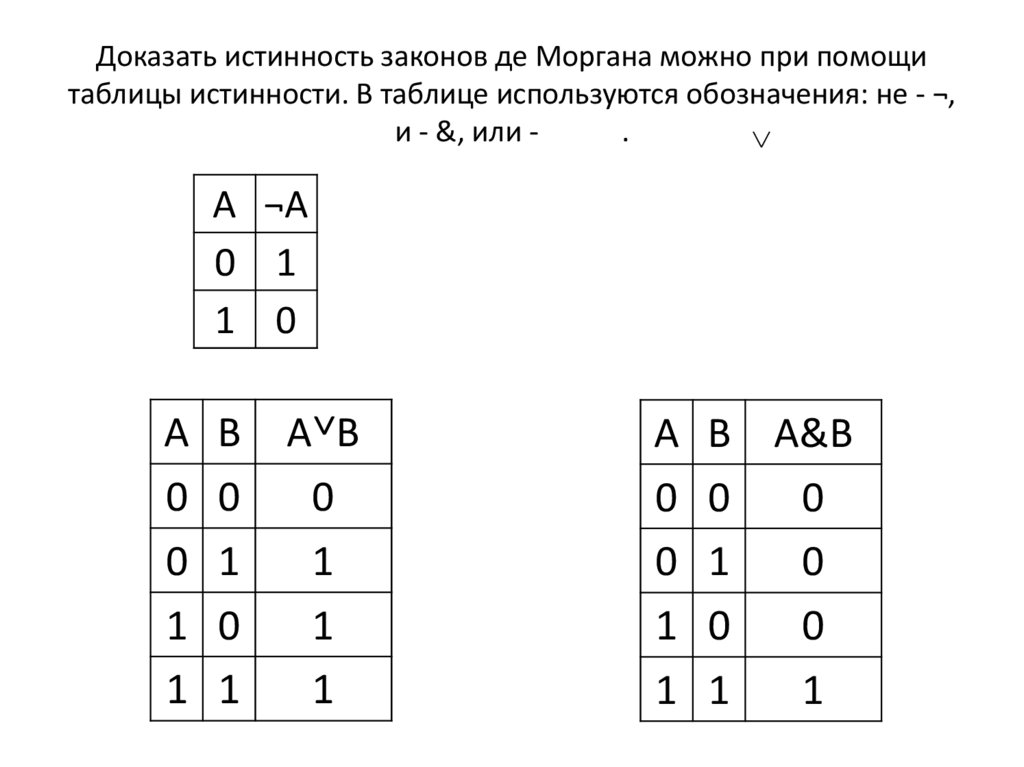
Доказать истинность законов де Моргана можно при помощитаблицы истинности. В таблице используются обозначения: не - ¬,
и - &, или .
A ¬A
0 1
1 0
A B
0 0
0 1
1 0
1 1
A˅B
0
1
1
1
A B A&B
0 0
0
0 1
0
1 0
0
1 1
1
6.
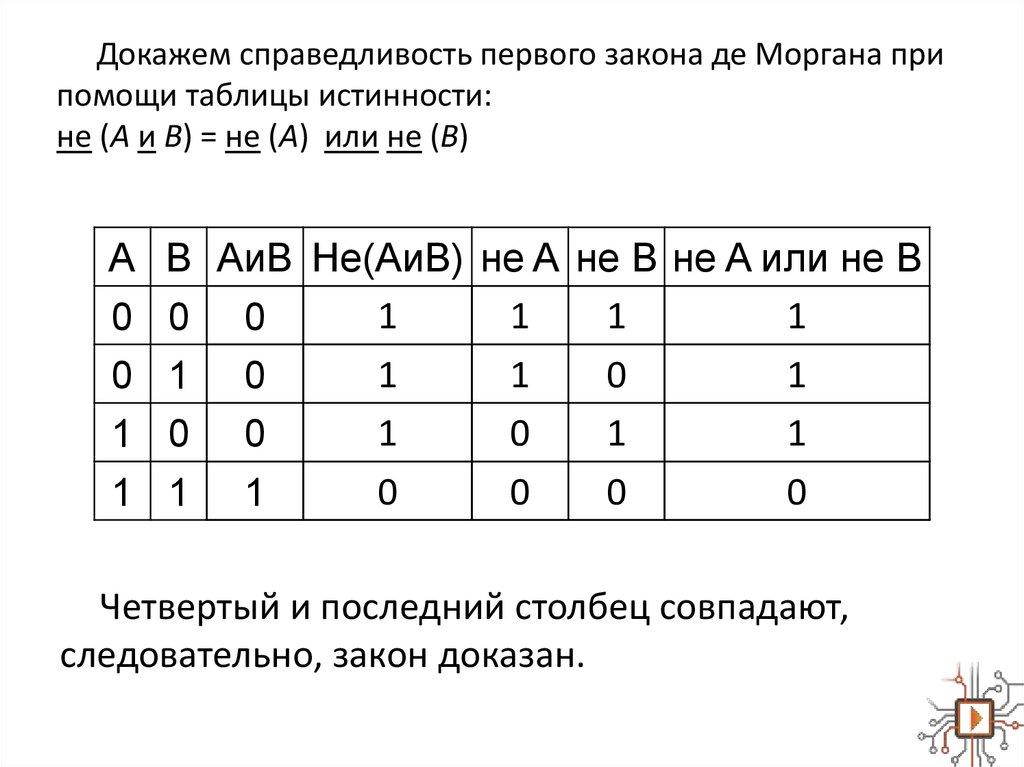
Докажем справедливость первого закона де Моргана припомощи таблицы истинности:
не (A и B) = не (A) или не (B)
A
0
0
1
1
B AиB Не(AиB) не A не B не A или не B
1
1
1
1
0 0
1
1
0
1
1 0
1
0
1
1
0 0
0
0
0
0
1 1
Четвертый и последний столбец совпадают,
следовательно, закон доказан.
7.
Задача 2. Даны массивы A[1:n], B[1:m]. Вставить элементы массиваB в массив A после его минимального элемента.
A
B
nmin
A
nmin
Постановка задачи
Дано: n-цел, A[1:n]-вещ, m-цел, B[1:m]-вещ
Результат:A[1:n+m] - вещ
При: nЄN, m ЄN, n+m≤lmax
Связь:∃nmin:∀ i=1,n a[nmin]≤a[i], ∄ t ϵ [1, nmin-1]: A[t]=A[nmin]
A[j]=A[i], i=n, nmin+1,шаг -1, j=n+m, nmin+m+1, шаг -1
A[nmin+i]=B[i], i=1,m.
8.
алг «план действий»нач
ввод(n, A[1:n], m, B[1:m])
поиск номера минимума в массиве A
сдвиг вправо элементов массива A,
расположенных после минимального
вставка элементов массива B в массив A
изменение длины массива A
вывод результата
кон
9.
Сдвиг элементов массива A вправо можноосуществлять различными способами.
1.
j:= n+m {номер позиции, на которую происходит сдвиг}
цикл от i:=n до nmin +1 шаг -1
A[j]:=A[i]
j:= j-1
кц
2.
{i – номер сдвигаемого элемента}
цикл от i:=1 до n - nmin
A[n+m-i+1]:=A[n-i+1]
кц
3.
цикл от i:=n до nmin+1 шаг -1
A[i+m]:=A[i]
кц
10.
Алг «вставка»Нач
ввод(n, A[1:n], m, B[1:m])
nmin:=1
цикл от i:=2 до n
если A[i] < A[nmin] то
nmin:=i
всё
кц
если nmin≠n то
цикл от i:=n до nmin +1 шаг -1
A[i+m]:=A[i]
кц
всё
цикл от i:=1 до m
A[nmin+i]:=B[i]
кц
Вывод (A[1:n+m])
кон
11.
Задача 3. Дан массив A[1:n]. Написать постановку задачи,алгоритм и программу для вычисления суммы элементов
массива, расположенных между первым и последним
отрицательными элементами (включительно).
Постановка задачи.
Дано: n-цел, a[1:n]-вещ
Результат:s или сообщение «нет отрицательных элементов» или
сообщение «один отрицательный элемент»,a[n1]
При: nЄN, n<=lmax
Связь: ∃ n1: n1=1,n: a[n1]<0, ∄ t: t=1,n1-1: a[t]<0.
∃ np: np=1,n: a[np]<0, ∄ q: q=np+1,n: a[q]<0.
np
s a[i ].
i n1
12.
Алг «сумма элементов, расположенных между первым и последнимотрицательным
элементом »
нач
ввод(n, a[1:n])
n1:=0{номер первого отрицательного элемента}
np:=0{номер последнего отрицательного элемента}
цикл от i:=1 до n
если a[i]<0 то
Если n1=0 то {это первый отрицательный элемент –
номер еще ни разу не изменился}
n1:=i
всё
{запоминаем его номер(это присваивание
происходит либо 1 раз, либо не выполняется ни разу )}
np:=i{запоминаем номер последнего отрицательного
элемента (для каждого отрицательного элемента) }
всё
кц
13.
если n1=0 {не найдено отрицательных элементов } товывод («нет отрицательных»)
иначе
если n1=np {не найдено двух отрицательных элементов} то
вывод («один отрицательный элемент», a[n1])
иначе
s:=0
цикл от i:=n1 до np
s:=s+a[i]
кц
вывод(s)
всё
всё
кон
14.
#include <stdio.h>#define lmax 20
int main()
{
float a[lmax],s;
int n,i,n1,np;
do{
printf(" введите n");
scanf("%d",&n);
}
while (n<=0||n>lmax);
printf(" введите %d ‘элементов\n",n);
for (i=1; i<=n;i++)
scanf("%f",&a[i]);
for (n1=np=0,i=1; i<=n;i++)
if (a[i]<0 )
{
if (n1==0 )
n1=i;
np=i;
}
15.
if (n1==0)printf (" нет отрицательных ");
else
if (n1==np)
printf (" один отрицательный элемент %8.3f",
a[n1]);
else
{
s=0;
for (i=n1; i<=np;i++)
s=s+a[i] ;
printf("s=%10.5f",s);
}
return 0;
}











 programming
programming








