Теория алгоритмов. Формальные способы задания алгоритмов

1. Теория алгоритмов. Формальные способы задания алгоритмов

Институт Информационных
Технологий

2.

Теория алгоритмов
На этой лекции:
Понятие алгоритма
Нормальные алгоритмы Маркова
Вычислимые функции

3. Понятие алгоритма

Алгоритм – точное предписание, определяющее вычислительный
процесс, ведущий к искомому результату. При этом требуется:
Чтобы исходные данные были заданы в конкретном алфавите и могли
принимать значения из некоторого множества
Чтобы процесс переработки данных состоял из дискретных шагов
Чтобы была исключена двузначность толкования (детерминированный)
Чтобы были указаны условия остановки процесса и то, что следует
считать результатом.
Замечание:
Понятие алгоритма не является строгим, так как не конкретизирует
понятие элементарного (дискретного) шага.

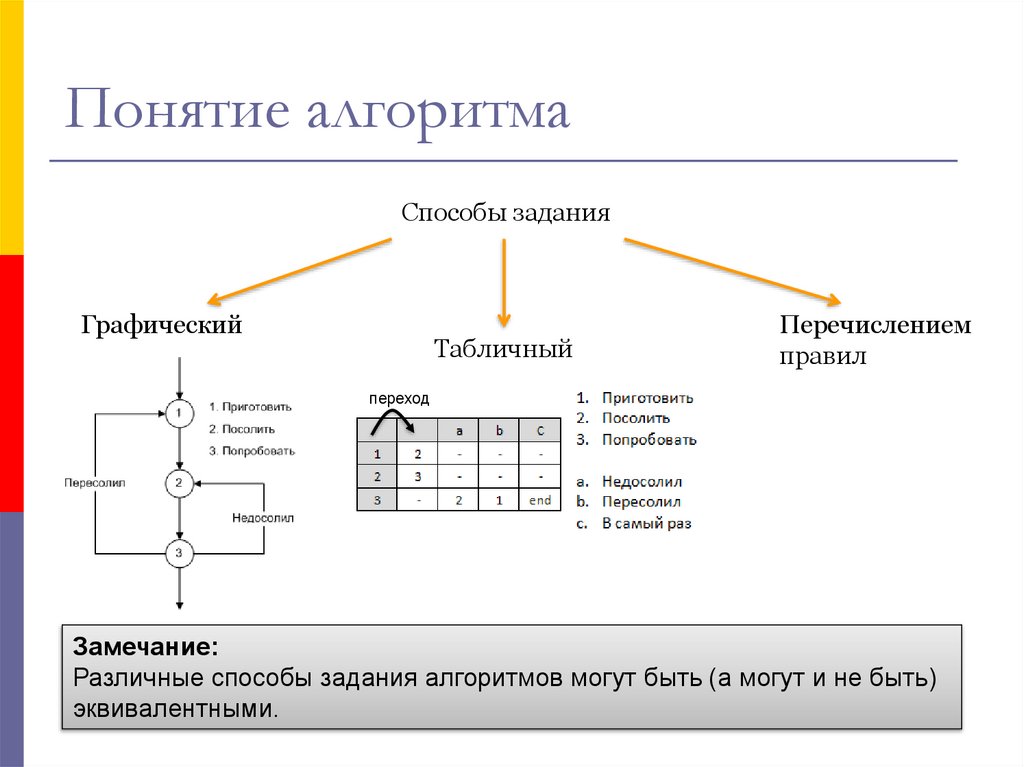
4. Понятие алгоритма

Способы задания
Графический
Табличный
Перечислением
правил
переход
Замечание:
Различные способы задания алгоритмов могут быть (а могут и не быть)
эквивалентными.

5.

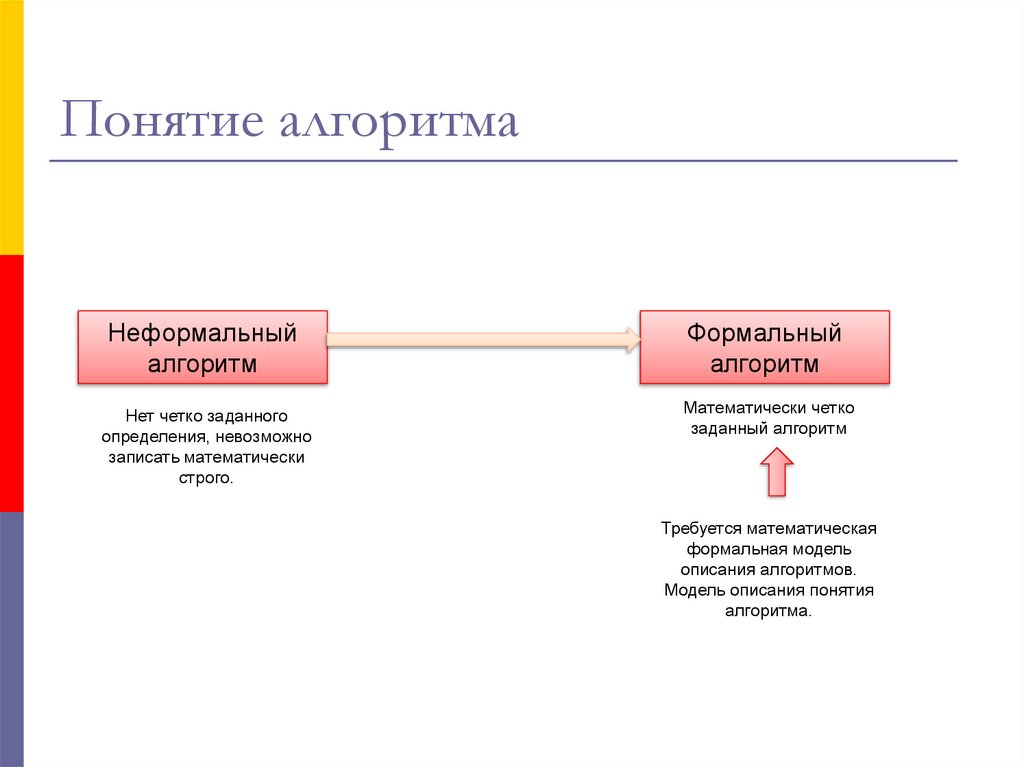
Понятие алгоритма
Неформальный
алгоритм
Формальный
алгоритм
Нет четко заданного
определения, невозможно
записать математически
строго.
Математически четко
заданный алгоритм
Требуется математическая
формальная модель
описания алгоритмов.
Модель описания понятия
алгоритма.

6.

Понятие алгоритма
Формальные способы описания понятия алгоритма:
Нормальный алгоритм Маркова (Марков А.А. в 1947г.)
Машина Тьюринга
Машина Поста
Автоматное
программирование
Рекурсивная функция (теория вычислимости)

7. Нормальный алгоритм Маркова

Нормальный алгоритм Маркова задаётся своим алфавитом и своей
схемой.
Алфавит представляет собой непустое множество символов,
включающее символ пустого слова. Любое непустое слово алфавита
составлено из символов алфавита.
Схема алгоритма задаётся конечным упорядоченным (это важно)
набором формул подстановок.
Пример:
Алфавит:
Слова:
Набор
команд
Подстановки:
Входными данными алгоритма может являться произвольная строка
символов над указанным алфавитом.
Пустое
слово

8. Нормальный алгоритм Маркова

Алгоритмический процесс заключается в многократном применении
операции подстановки к строке входных данных.
Структура операции подстановки:
1
• В наборе подстановок ищем первую, первое слово которой
встречается в строке данных алгоритма.
2
• В строке данных ищем самое первое вхождение первого слова
данные
найденной подстановки.
3
• Выполняем преобразование строки данных, заключающееся в замене
первого слова подстановки в найденной позиции на второе.
Набор
команд
Останов процесса:
1
• Если ни одна подстановка не может быть применена
2
• Если становится известно, что процесс подстановок не может
быть завершён.

9. Пример 1

Алфавит:
Строка данных:
данные
Система подстановок:
Набор
команд
Алгоритмический процесс:
Выходная строка данных:
результат

10. Пример 2

Алфавит:
Строка данных:
Система подстановок:
Алгоритмический процесс:
Вывод: алгоритм неприменим

11. Нормальный алгоритм Маркова

Всякий нормальный алгоритм Маркова определяет отображение (или
функцию отображения) множества допустимых входных слов во
множество выходных слов.
Такое отображение иногда называется нормальным Марковским
отображением, а функция отображения называется вычислимой
по Маркову функцией.

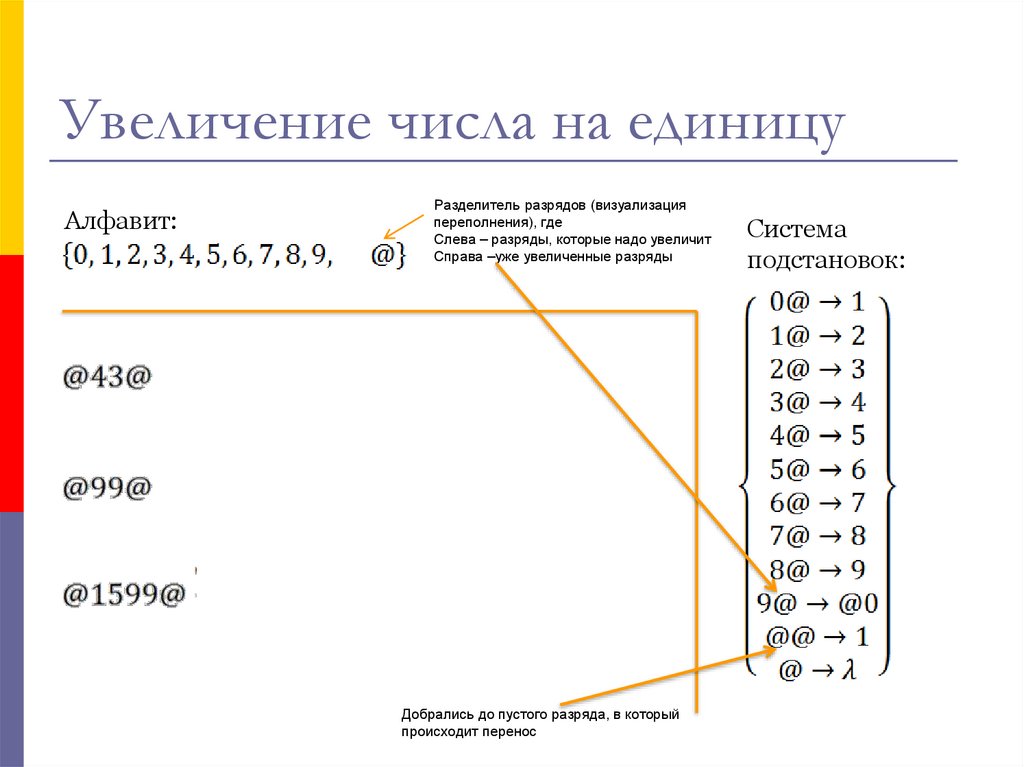
12. Увеличение числа на единицу

Алфавит:
Разделитель разрядов (визуализация
переполнения), где
Слева – разряды, которые надо увеличит
Справа –уже увеличенные разряды
Добрались до пустого разряда, в который
происходит перенос
Система
подстановок:

13. Увеличение числа на единицу

Алфавит:
Разделитель разрядов (визуализация
переполнения), где
Слева – разряды, которые надо увеличит
Справа –уже увеличенные разряды
Добрались до пустого разряда, в который
происходит перенос
Система
подстановок:

14. Логическое сложение двух бинарных чисел

Алфавит:
Система подстановок:
Логическое сложение = ИЛИ (OR) (V)
A or B, A OR B, A ИЛИ B, А или В, A V B, A v B

15.

Вычислимые функции

16. Вычислимая функция

Функция f называется вычислимой, если существует алгоритм,
перерабатывающий всякий объект x, для которого определена
функция f, в объект f(x), и не применимый ни к какому x, для которого
функция f не определена.
Пример:
Функция f(x)=x+1 согласно представленному определению, является
вычислимой, т.к. нам удалось построить нормальный алгоритм
Маркова увеличения числа на 1.

17.

Вычислимая функция
?
Всякую ли функцию можно назвать вычислимой, то есть
создать алгоритм, реализующий эту функцию?
Это мы сейчас и рассмотрим
?
Всякий ли алгоритм описывает функцию?
По определению, Всякий нормальный алгоритм Маркова определяет отображение
(или функцию отображения), а значит и функцию, называемую – вычислимой по
Маркову.

18. Вычислимая функция

Функцию f:X→Y будем называть частичной, если она определена не
для всех значений x∈X. Множество тех x∈X, для которых однозначно
определяется значение функции f, будем называть областью
определения функции f.
Будем называть далее простейшими функции:
Пример 2 – алгоритма Маркова (слайд-11) –
когда алгоритм не применим к некоторым
последовательностям входных данных

19.

Вычислимая функция
Замечание:
Рекурсия является удобным способом вычисления значений
функций.
Замечание:
Рекурсивные функции являются вычислимыми по определению. Есть
основания полагать, что верно и обратное.

20. Примитивно рекурсивная функция

Пусть даны частичные функции g и h. Частичная функция f получена
из функций g и h примитивной рекурсией, если:
Номер шага 0,1,2,3,4 …
Замечание:
Для n=0 указанные уравнения принимают вид:
Доказательство по индукции
Арифметическая прогрессия
Функция вычисления факториала

21. Примитивно рекурсивная функция

Частичная функция f называется примитивно рекурсивной
относительно множества частичных функций Ω, если f получается из
функций множества Ω и простейших функций конечным числом
операций подстановки и примитивной рекурсии.
Если Ω = Ø, то функция f получается только из простейших функций
и её называют просто примитивно рекурсивной.

22. Примитивно рекурсивная функция

Пример:
- примитивно рекурсивная функция
Пример:
- примитивно рекурсивная функция

23. Частично рекурсивная функция

Пусть дана частичная функция f. Операцией минимизации назовём
функцию M:
Частичная функция f называется частично рекурсивной
относительно множества частичных функций Ω, если f получается из
функций множества Ω и простейших функций конечным числом
операций подстановки, примитивной рекурсии и минимизации.
Пример:
- частично рекурсивная функция

24.

Вычислимая функция
рекурсивные функции:
2) Множество примитивно
рекурсивных функции
? Функция Аккермана –
вычислимая, но не примитивнорекурсивная
1) Множество частично
рекурсивных функции
3) Множество
общерекурсивных функций
Доказал Гёдель
Множество
вычислимых функций
Множество частично рекурсивных функции («рекурсивные функции, определенные на части
множества возможных аргументов»)
Множество общерекурсивных функций («рекурсивные функции, определенные на всём
множестве возможных аргументов»)
Общерекурсивные функции — это подмножество частично рекурсивных функций,
определённых для всех значений аргументов

25. Тезис Чёрча

Класс алгоритмически вычислимых частичных функций совпадает с
классом всех частично рекурсивных функций.
Замечание:
Доказать или опровергнуть тезис Чёрча нельзя, потому как он
представляет утверждение относительно понятия алгоритмически
вычислимой функции, которое не является строгим.

26.

Выводы
Примитивные функции соответствуют программным функциям, в которых
используется только арифметические операции, а также условный
оператор и оператор арифметического цикла (оператор цикла, в котором
число итераций известно на момент начала цикла)
оператор цикла while, в котором число итераций заранее неизвестно, и в
принципе, может быть бесконечным, то он переходит в класс частично
рекурсивных функций.

27.

Выводы
Алгоритмически разрешимая арифметическая задача может быть
реализована при помощи некоторого фиксированного набора функций при
помощи подстановки, рекурсии и минимизации.