Элементарная статистика

1.

ЭЛЕМЕНТАРНАЯ СТАТИСТИКА

2.

Предположим, что теперь нам нужно определить вероятность выпадения
только одного герба в трех бросаниях. Имеется следующие возможные исходы
(Г — герб; Р — решка):
ГГГ
ГРГ
РРР
ГГР
РГГ
[РГР]
[ГРР]
[РРГ]
Как установить общее количество вариантов?
В скобках взяты те комбинации, которые удовлетворяют нашим требованиям,
т. е. они содержат только один герб. Так как имеется 8 различных комбинаций,
вероятность получения только одного герба при трех бросаниях равна 3/8.
Полученное нами число представляет собой число возможных комбинаций из
трех по одному. Обобщая этот пример, можно определить число возможных
сочетаний из п элементов по r. Это число символически изображается так n
Как установить общее количество вариантов,
удовлетворяющих условию?
r

3.

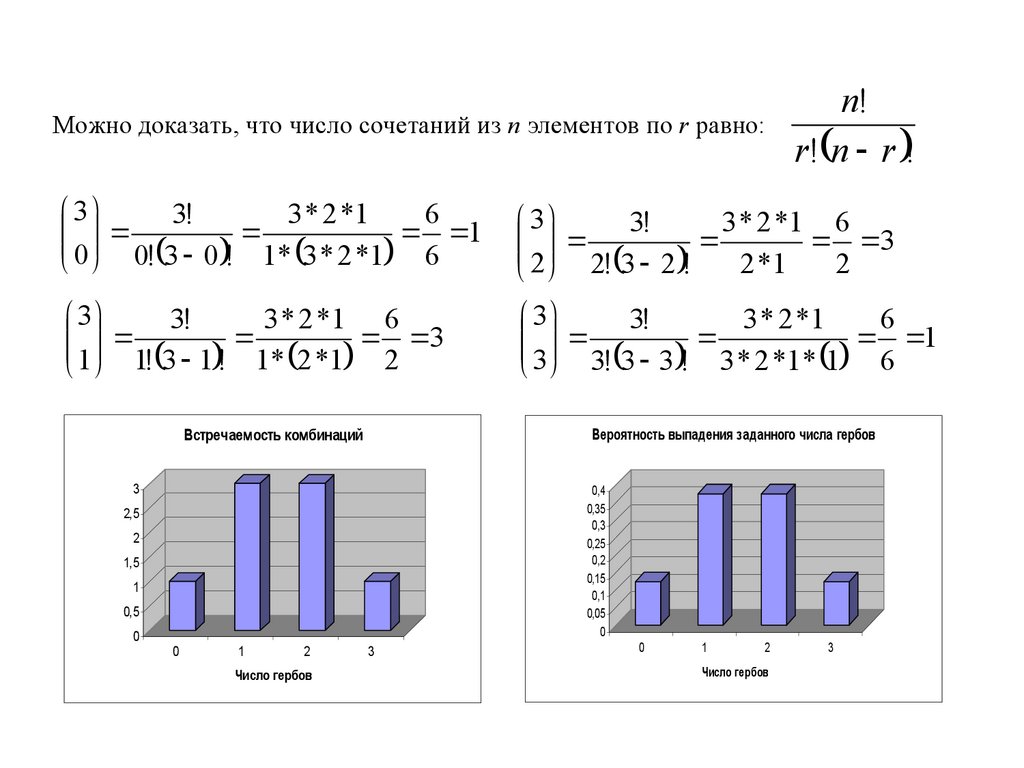
Можно доказать, что число сочетаний из п элементов по r равно:
n!
r! n r !
3
3!
3 * 2 *1
6
1
0 0! 3 0 ! 1* 3 * 2 *1 6
3
3!
3 * 2 *1 6
3
2 *1
2
2 2! 3 2 !
3
3!
3 * 2 *1 6
3
1 1! 3 1 ! 1* 2 *1 2
3
3!
3 * 2 *1
6
1
3 3! 3 3 ! 3 * 2 *1* 1 6
Вероятность выпадения заданного числа гербов
Встречаемость комбинаций
3
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
2,5
2
1,5
1
0,5
0
0
1
2
Число гербов
3
0
1
2
Число гербов
3

4.

Эксперимент бросания монеты обладает четырьмя особенностями:
1) в каждом испытании (или бросании) имеется только два возможных исхода
(назовем их «успех» или «неудача»);
2) исход каждого испытания не зависит от предыдущих исходов;
3) вероятность успеха не меняется от испытания к испытанию;
4) испытания повторяются заданное число раз.
Распределение вероятностей, соответствующее указанному нами типу
эксперимента, называется биномиальным распределением.
В каком случае биномиальное распределение может быть
использовано для оценки вероятности успеха поисковых
скважин?
Четыре перечисленных выше характеристики должны предполагаться
справедливыми: допущения подобного рода кажутся наиболее приемлемыми при
использовании метода «дикой кошки» при поисках в сравнительно мало
изученном бассейне.
В предположении о справедливости биномиального распределения каждый
результат применения метода «дикой кошки» может быть классифицирован либо
как «открытие» («успех») либо как пустая скважина («неудача»).
Последовательные испытания предполагаются независимыми, т. е. успех или
неудача в одной скважине не влияет на результат опробования в другой скважине.
Наконец, биномиальное распределение оказывается подходящим, если
фиксированное число скважин будет пробурено в процессе разведки или в течение
единичного периода времени (например, бюджетного цикла), для которого
проведено прогнозирование.

5.

За вероятность р открытия нефтяного или газового месторождения методом
«дикой кошки» принимаются широко используемые в промышленности
отношения, характеризующие успех бурения, которые были наблюдены в
процессы бурения в аналогичных регионах, или аналогичные отношения,
полученные компаниями, делающими оценки, или же просто субъективные
аналогичные характеристики. Для определения вероятности р в биномиальной
модели в поисковом бурении предусмотрены следующие этапы:
1.
2.
3.
4.
5.
Вероятность «успеха» бурения скважины обозначим через р,
Вероятность «неудачи» бурения обозначим через 1—р,
Вероятность того, что в результате последовательного бурения п скважин
n
методом «дикой кошки» все окажутся пустыми, есть P 1 p
Вероятность того, что п-я пробуренная скважина окажется продуктивной,
причем п—1 предыдущих скважин окажутся пустыми, равна P (1 p ) n 1 p
Вероятность появления одной продуктивной скважины в
последовательности п скважин, пробуренных методом «дикой кошки»,
n 1
есть
P n 1 p p
так как продуктивной может оказаться любая из п скважин;

6.

6.
вероятность того, что будет пробурено п—r пустых скважин, за которыми
последует r продуктивных, есть P 1 p n r p r
7. Однако п-r пустых скважин и r продуктивных скважин могут быть выбраны
n!
различными способами.
n способами, или, что эквивалентно,
n r !r!
r
Так, вероятность того, что в программе бурения методом «дикой кошки» среди
п скважин получим r продуктивных, равна
n!
1 p n r p r
P
n r !r!
Это — формула биномиального распределения, задающая вероятность
получения r успехов в последовательности п независимых испытаний,
вероятность успеха в каждом из которых равна p

7.

В других практических задачах, в которых основные допущения отличны от
указанных выше, могут быть использованы другие дискретные вероятностные
распределения. Предположим, например, что геологоразведочная компания
намеревается открыть два новых месторождения в мало изученном бассейне, пред­
полагаемом перспективным, и намеревается пробурить столько скважин, сколько
потребуется для того, чтобы достичь этой цели. Мы можем исследовать вероятность
того, что для этого потребуется 2,3,4..., до п разведочных скважин до того как будет
обнаружено две продуктивных скважины. Можно допустить, что требуется
наложить те же условия, которые были перечислены для биномиального
распределения, исключая относящееся к числу испытаний условие, которое теперь
не является фиксированным.
Вероятностное распределение, соответствующее такому эксперименту, называется
отрицательным биномиальным, и его определение очень напоминает определение
биномиального распределения. Как и в предыдущем примере, р есть вероятность
появления продуктивной скважины и r есть число «успехов» или продуктивных
скважин. Однако п, число испытаний, не задано. Вместо этого можно найти
вероятность того, что будет пробурено х пустых скважин раньше, чем будет сделано
r открытий. Отрицательное биномиальное распределение имеет вид:
r x 1
x r
1 p p
P
x

8.

Для практических вычислений формула может быть представлена в виде:
r x 1 !
1 p x p r
P
r 1 ! x!

9.

Справочные данные
Вероятность того, что в программе бурения методом
«дикой кошки» среди п скважин получим r продуктивных
n!
1 p n r p r
P
n r !r!
Вероятность того, что будет пробурено х пустых
скважин раньше, чем будет сделано r открытий
r x 1 !
x r
1 p p
P
r 1 ! x!
Факториалы
0
1
2
3
4
5
6
7
8
9
10
1
1
2
6
24
120
720
5040
40320
362880
3628800

10.

Задание
Предполагается пробурить 5 независимых поисковых. Для того, чтобы
результат можно было считать положительным, необходимо, чтобы как
минимум две скважины были успешными.
1. В приложении 1 представлена таблица испытаний скважин в исследуемом
регионе. Необходимо проанализировать результаты испытаний скважин,
оценить вероятность успеха бурения в рассматриваемом регионе.
2. В регионе предлагается пробурить 5 независимых поисковых скважин. Для
того, чтобы результат можно было считать положительным, необходимо,
чтобы как минимум две скважины были успешными. Какова вероятность
такого события?
3. Какова вероятность того, что одна скважина окажется продуктивной в
процессе разведки с пятью скважинами?
4. Какова вероятность того, что вся программа будет полностью безуспешной и
мы не получим ни одной продуктивной скважины?
5. Оцените, как изменится вероятность успеха, если необходимым условием
будет успех третьей скважины
6. Постройте дискретное распределение, задающее вероятность успеха в
программе бурения пяти скважин.