Similar presentations:
Аксиомы. Точки и прямые. Повторение по геометрии за курс 7 класса
1. Повторение по геометрии за курс 7 класса
2. Аксиомы Точки и прямые
АКСИОМЫТОЧКИ И ПРЯМЫЕ
Какова бы не была прямая, существуют точки,
принадлежащие этой прямой, и точки не
принадлежащие ей.
В
В
А
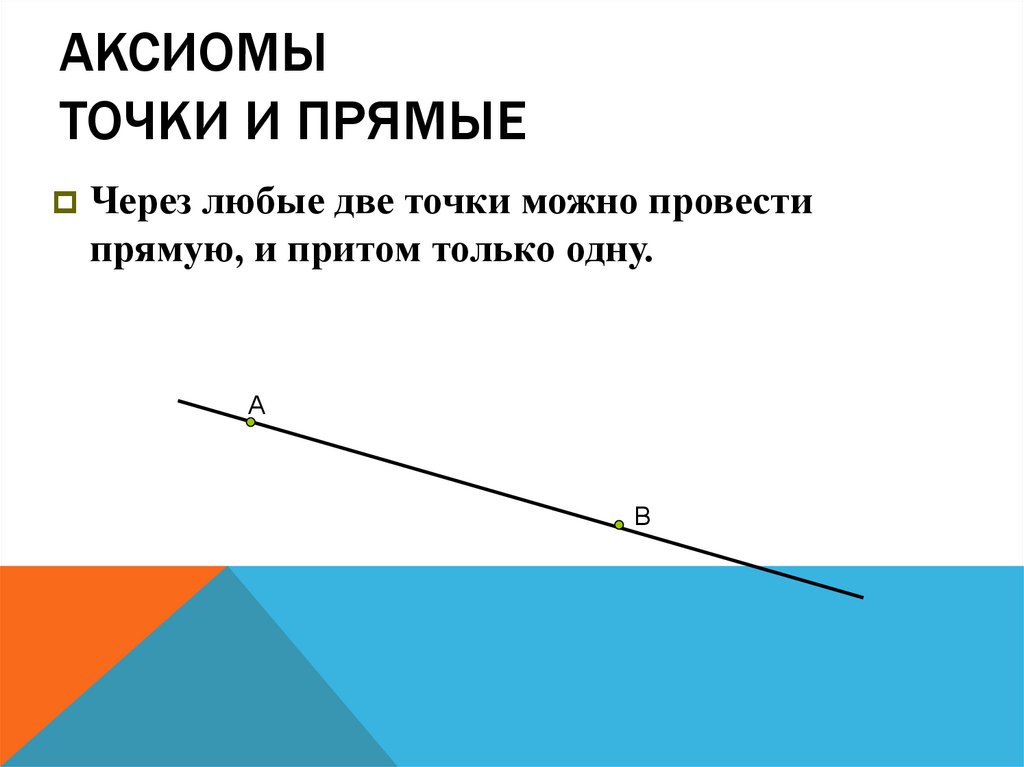
3. Аксиомы точки и прямые
АКСИОМЫТОЧКИ И ПРЯМЫЕ
Через любые две точки можно провести
прямую, и притом только одну.
А
В
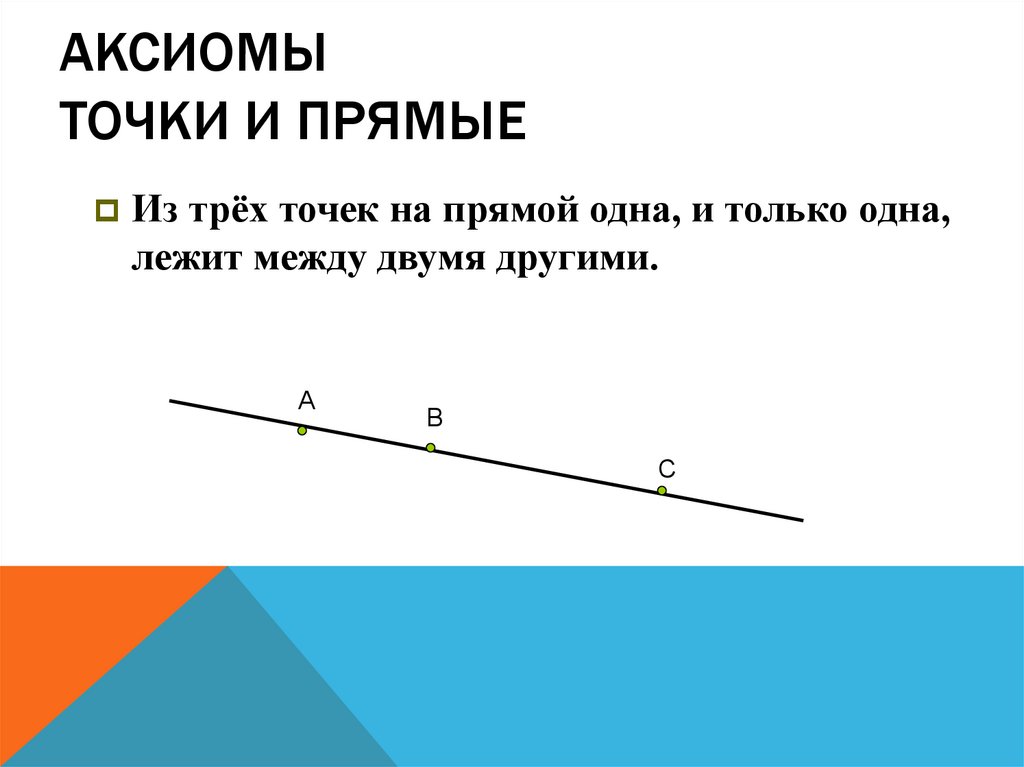
4. Аксиомы точки и прямые
АКСИОМЫТОЧКИ И ПРЯМЫЕ
Из трёх точек на прямой одна, и только одна,
лежит между двумя другими.
А
В
С
5. Аксиомы Отрезки и их длины
АКСИОМЫОТРЕЗКИ И ИХ ДЛИНЫ
Каждый отрезок имеет определённую длину.
А
В
АВ = 6 см
6. Аксиомы Отрезки и их длины
АКСИОМЫОТРЕЗКИ И ИХ ДЛИНЫ
Длина отрезка равна сумме длин частей, на
которые он разбивается любой внутренней
точкой.
А
В
С
АВ+ВС=АС
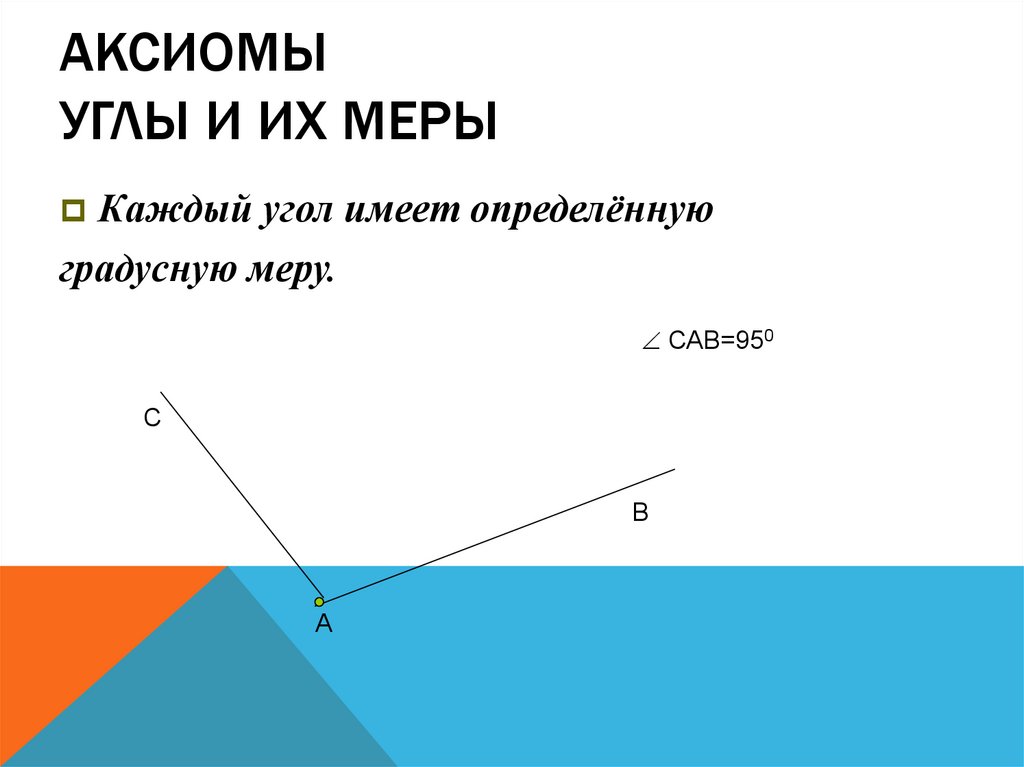
7. Аксиомы Углы и их меры
АКСИОМЫУГЛЫ И ИХ МЕРЫ
Каждый угол имеет определённую
градусную меру.
САВ=950
С
В
А
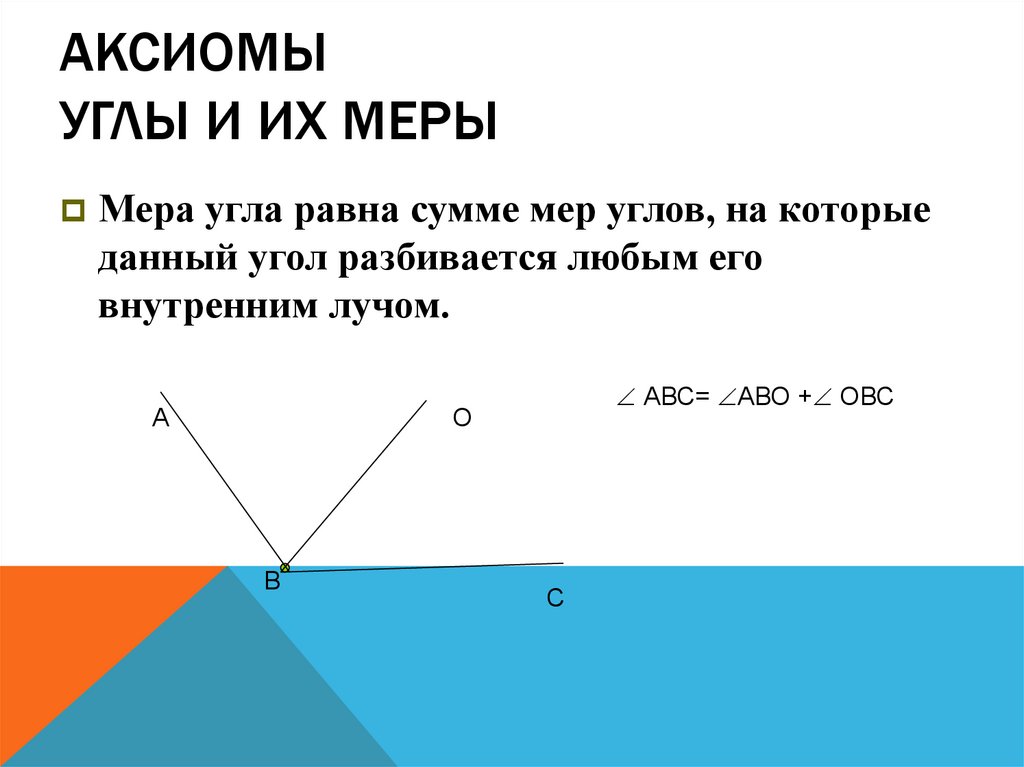
8. Аксиомы Углы и их меры
АКСИОМЫУГЛЫ И ИХ МЕРЫ
Мера угла равна сумме мер углов, на которые
данный угол разбивается любым его
внутренним лучом.
А
АВС= АВО + ОВС
О
В
С
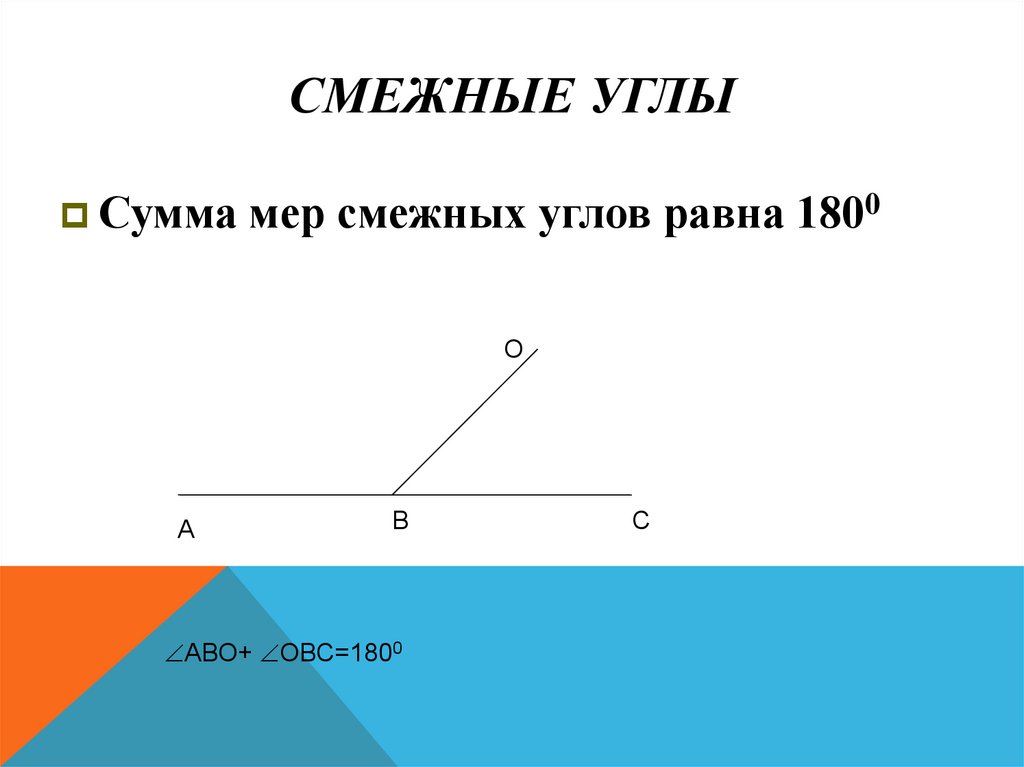
9. Смежные углы
СМЕЖНЫЕ УГЛЫСумма мер смежных углов равна 1800
О
А
В
АВО+ ОВС=1800
С
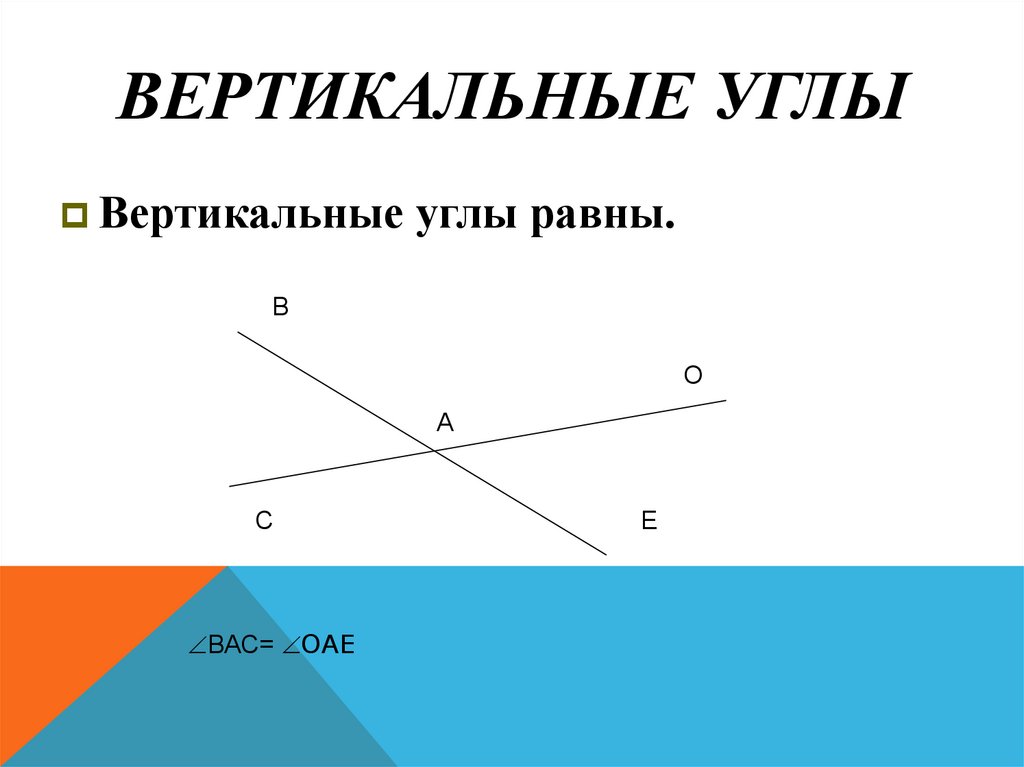
10. Вертикальные углы
ВЕРТИКАЛЬНЫЕ УГЛЫВертикальные углы равны.
В
О
А
С
ВАС= ОАЕ
Е
11. Параллельные прямые определение
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕОПРЕДЕЛЕНИЕ
Прямые называются параллельными, если
-они лежат в одной плоскости
-они не пересекаются
а
в
а в
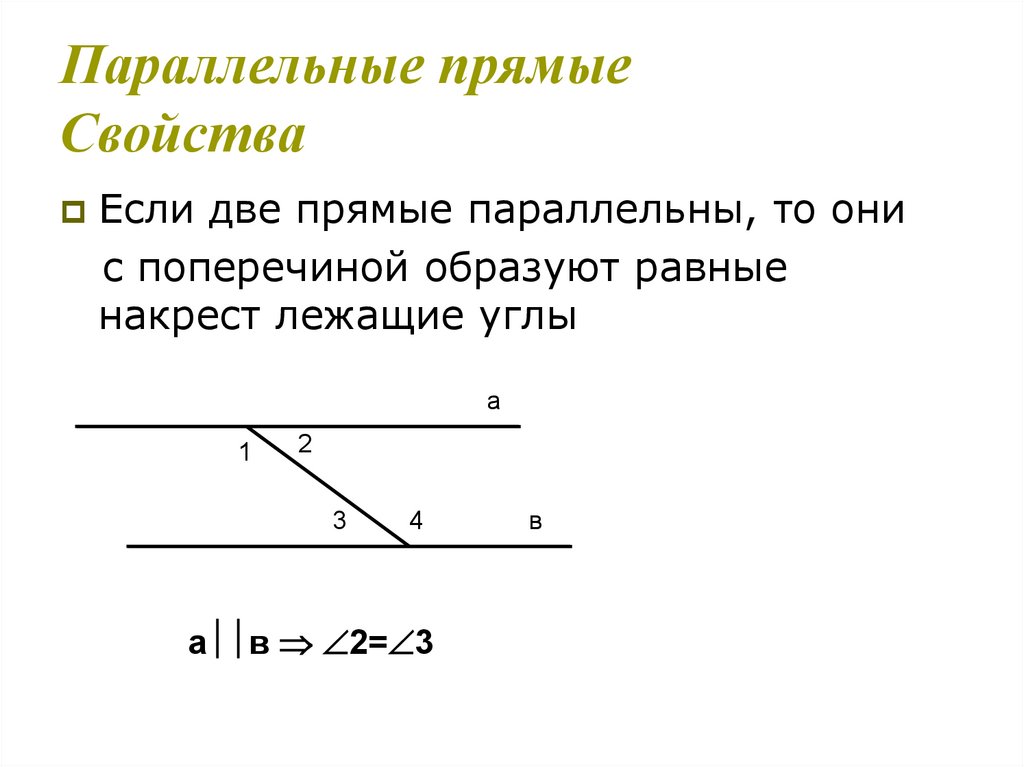
12. Параллельные прямые Признаки
ПАРАЛЛЕЛЬНЫЕПРЯМЫЕ
Параллельные
прямые
ПРИЗНАКИ
Свойства
Если
две прямые параллельны, то они
параллельны
Если две прямые с поперечиной образуют равные накрест лежащие углы, то прямые
с поперечиной образуют равные
накрест лежащие углы
а
1
2
3
4
а в
2= 3
2= 3
а в
в
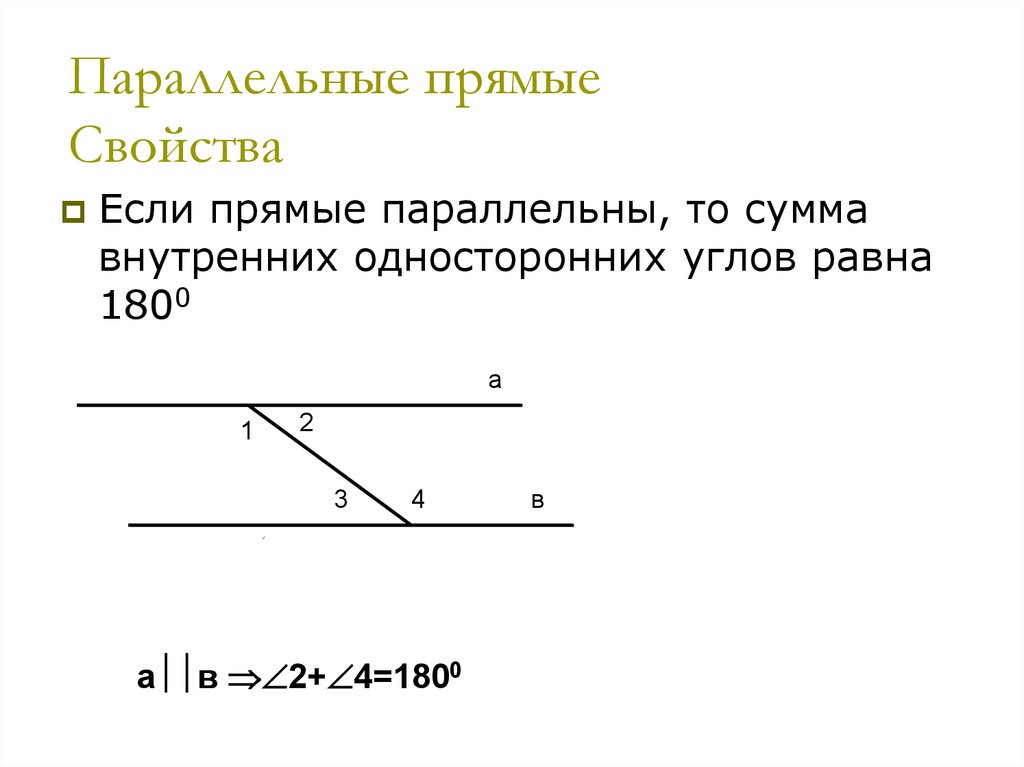
13. Параллельные прямые Признаки
ПАРАЛЛЕЛЬНЫЕПРЯМЫЕ
Параллельные
прямые
ПРИЗНАКИ
Свойства
Если прямые
сумма внутренних
параллельны,
односторонних
то сумма
Если сумма внутренних односторонних углов равна 180 0 ,то прямые параллельны
внутренних
углов
равна односторонних
1800 ,то прямыеуглов равна
0
параллельны
180
а
1
2
3
4
0 а в0
2+ 4=180
а в
2+ 4=180
в
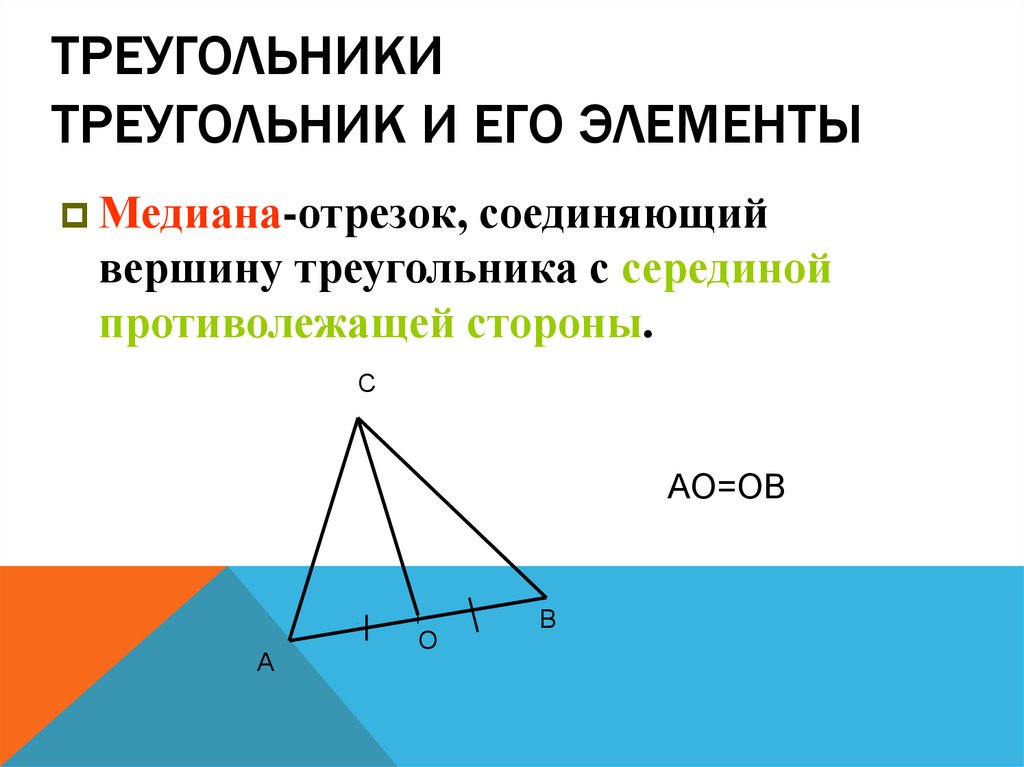
14. Треугольники Треугольник и его элементы
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Медиана-отрезок, соединяющий
вершину треугольника с серединой
противолежащей стороны.
С
АО=ОВ
А
О
В
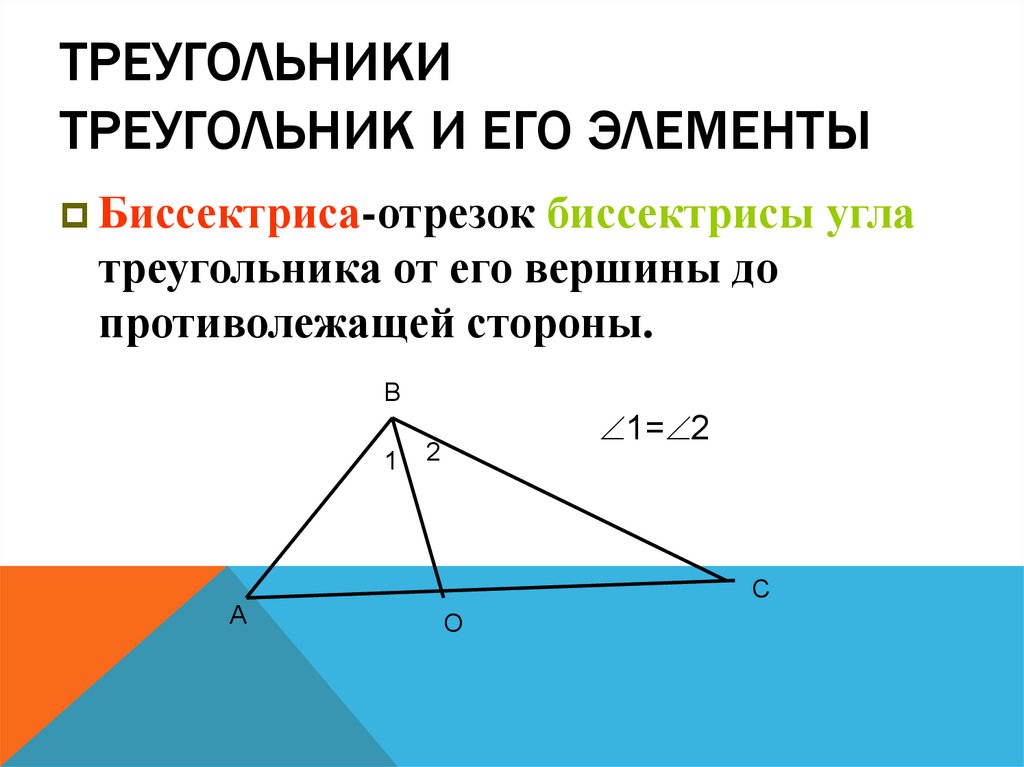
15. Треугольники Треугольник и его элементы
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Биссектриса-отрезок биссектрисы угла
треугольника от его вершины до
противолежащей стороны.
В
1
А
1= 2
2
С
О
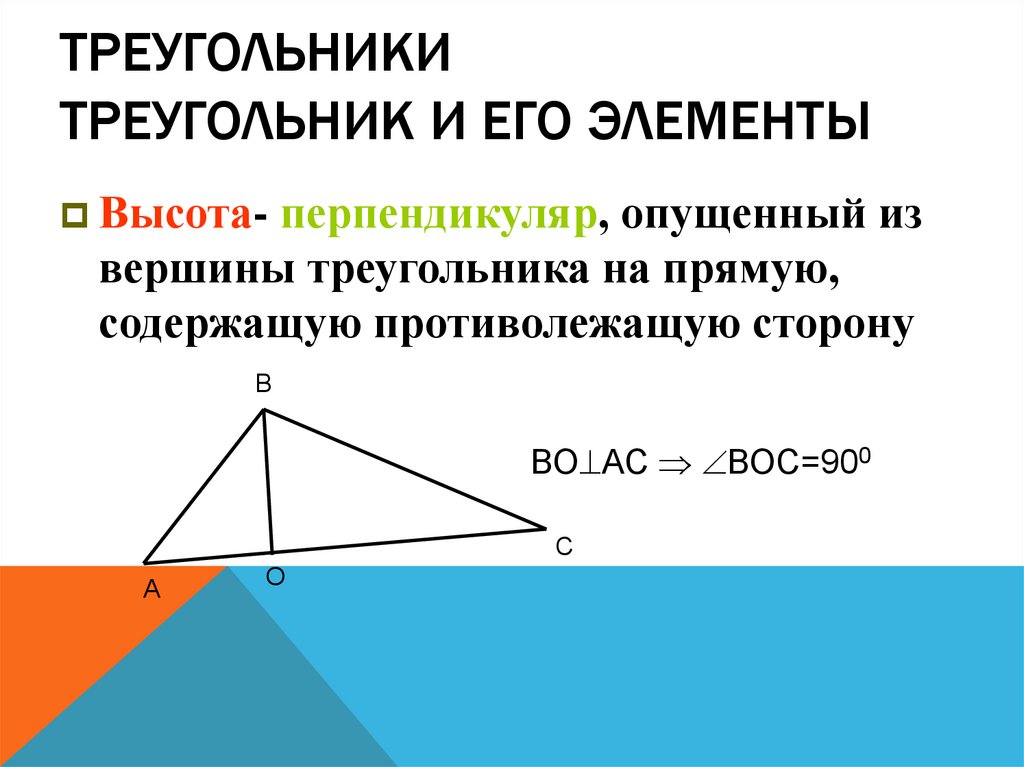
16. Треугольники Треугольник и его элементы
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Высота- перпендикуляр, опущенный из
вершины треугольника на прямую,
содержащую противолежащую сторону
В
ВО АС ВОС=900
С
А
О
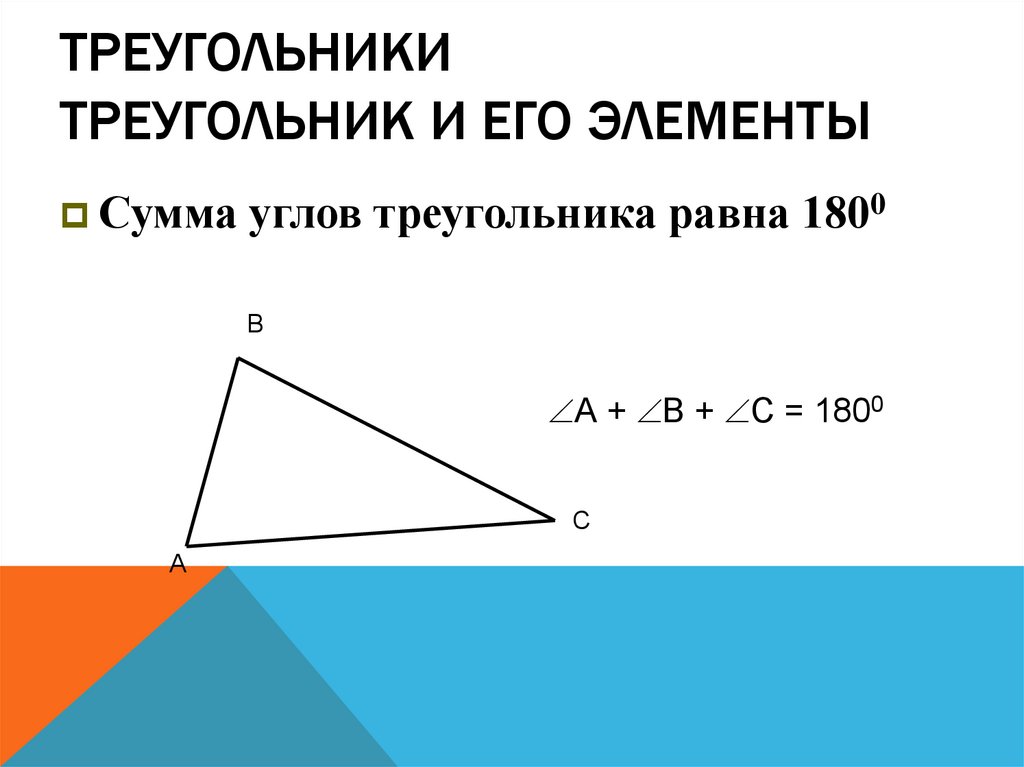
17. Треугольники Треугольник и его элементы
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Сумма углов треугольника равна 1800
В
А + В + С = 1800
С
А
18. Треугольники Треугольник и его элементы
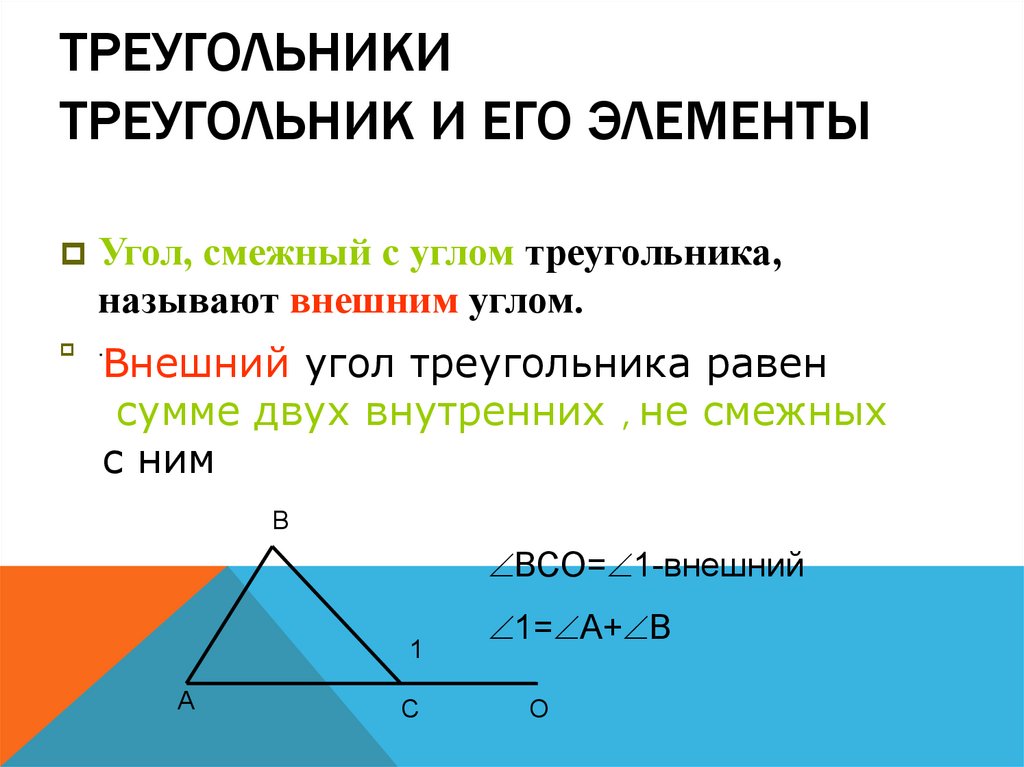
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Угол, смежный с углом треугольника,
называют внешним углом.
.
Внешний угол треугольника равен
сумме двух внутренних , не смежных
с ним
В
ВСО= 1-внешний
1
А
С
1= А+ В
О
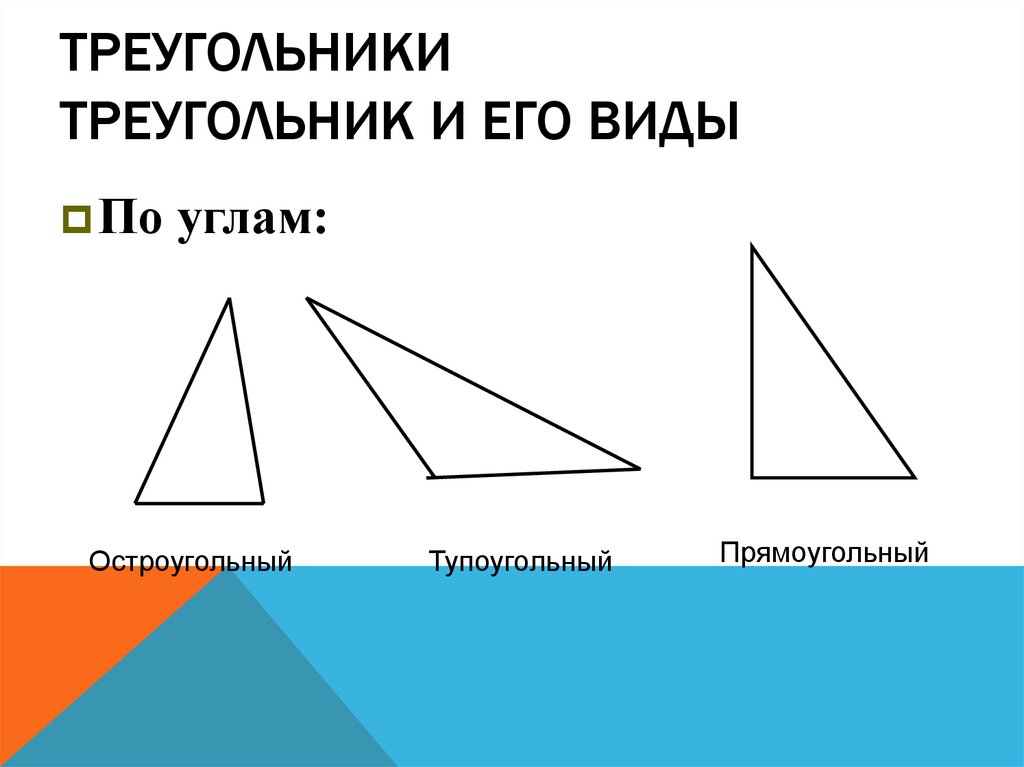
19. Треугольники Треугольник и его виды
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИК И ЕГО ВИДЫ
По углам:
Остроугольный
Тупоугольный
Прямоугольный
20.
ТреугольникиТреугольник и его виды
Треугольники
Равнобедренные
Равносторонние
Неравнобедренные
Неравносторонние
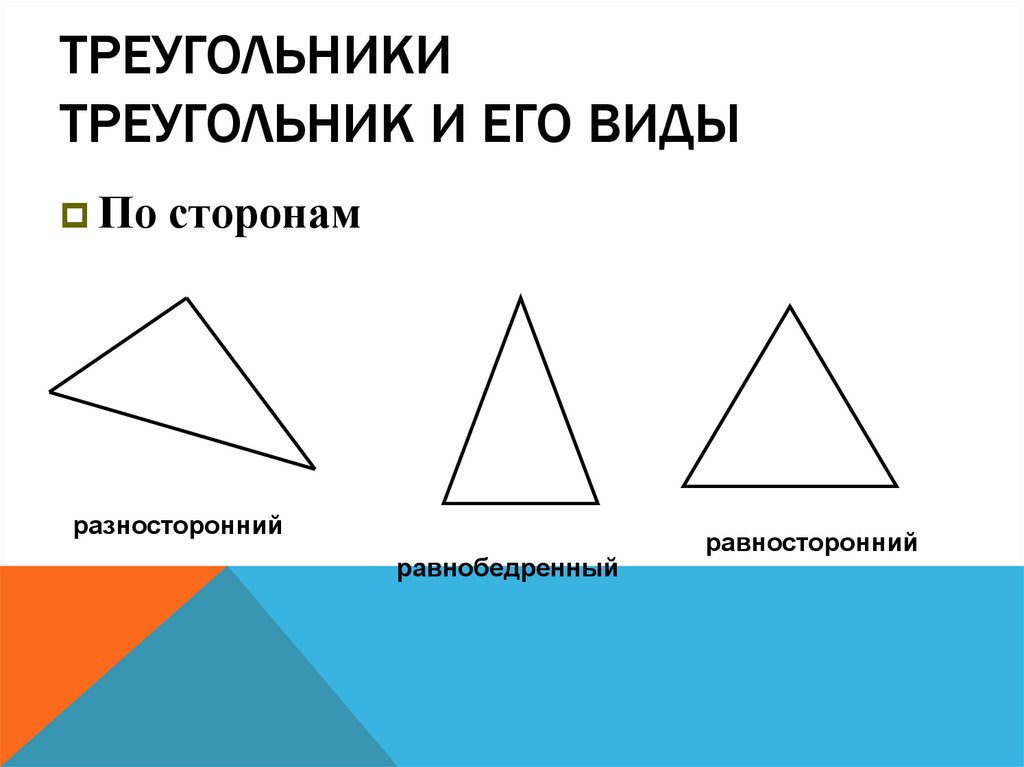
21. Треугольники Треугольник и его виды
ТРЕУГОЛЬНИКИТРЕУГОЛЬНИК И ЕГО ВИДЫ
По сторонам
разносторонний
равнобедренный
равносторонний
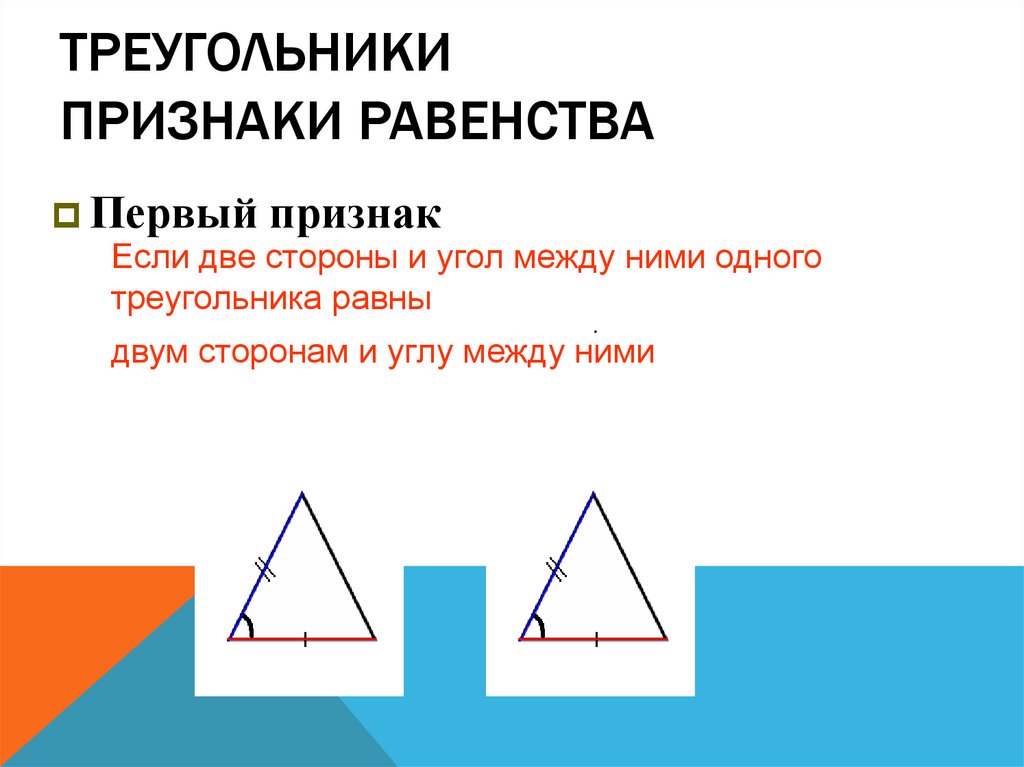
22. Треугольники Признаки равенства
ТРЕУГОЛЬНИКИПРИЗНАКИ РАВЕНСТВА
Первый признак
двеи стороны
и угол
две Если
стороны
угол между
нимимежду ними одного
треугольника равны
двум сторонам и углу между ними.
двум сторонам и углу между ними
23. Треугольники Признаки равенства
ТРЕУГОЛЬНИКИПРИЗНАКИ РАВЕНСТВА
Второй признак:торона и два прилежащих к ней
угла
Если сторона и два прилежащих к ней угла
одного треугольника равны стороне и двум
прилежащим к ней углам другого
треугольника, то такие треугольники
равны
24. Треугольники Признаки равенства
ТРЕУГОЛЬНИКИПРИЗНАКИ РАВЕНСТВА
Третий признак
Если три стороны одного треугольника
равны трем сторонам другого
треугольника соответственно, то такие
треугольники равны
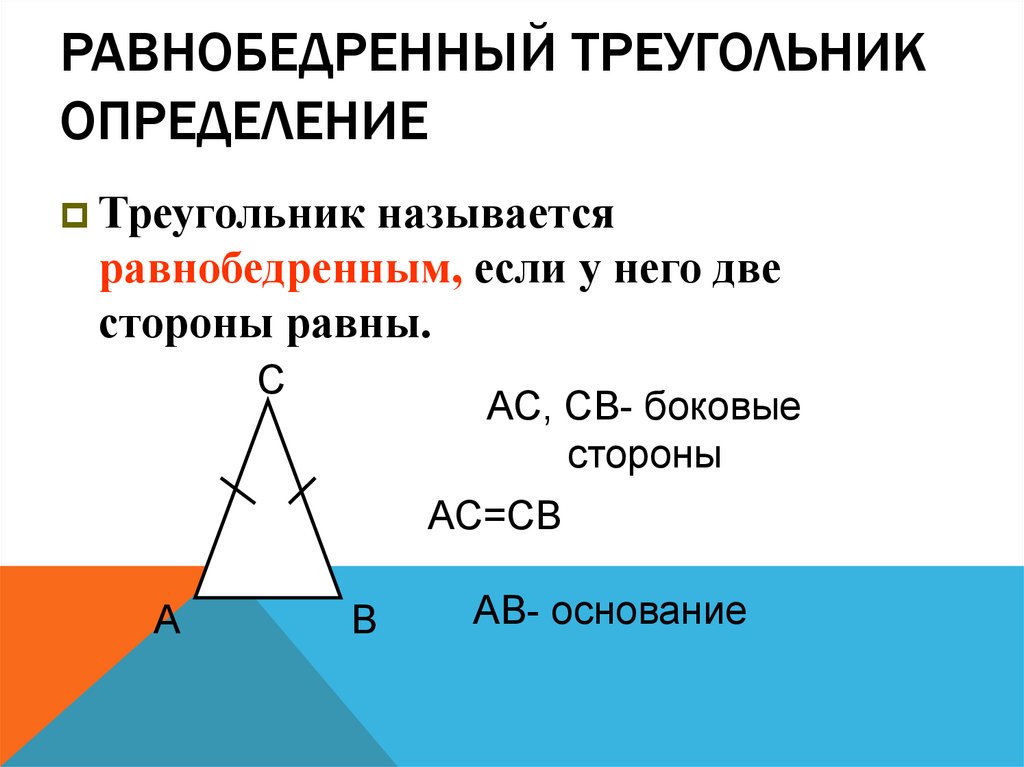
25. Равнобедренный треугольник Определение
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИКОПРЕДЕЛЕНИЕ
Треугольник называется
равнобедренным, если у него две
стороны равны.
С
АС, СВ- боковые
стороны
АС=СВ
А
В
АВ- основание
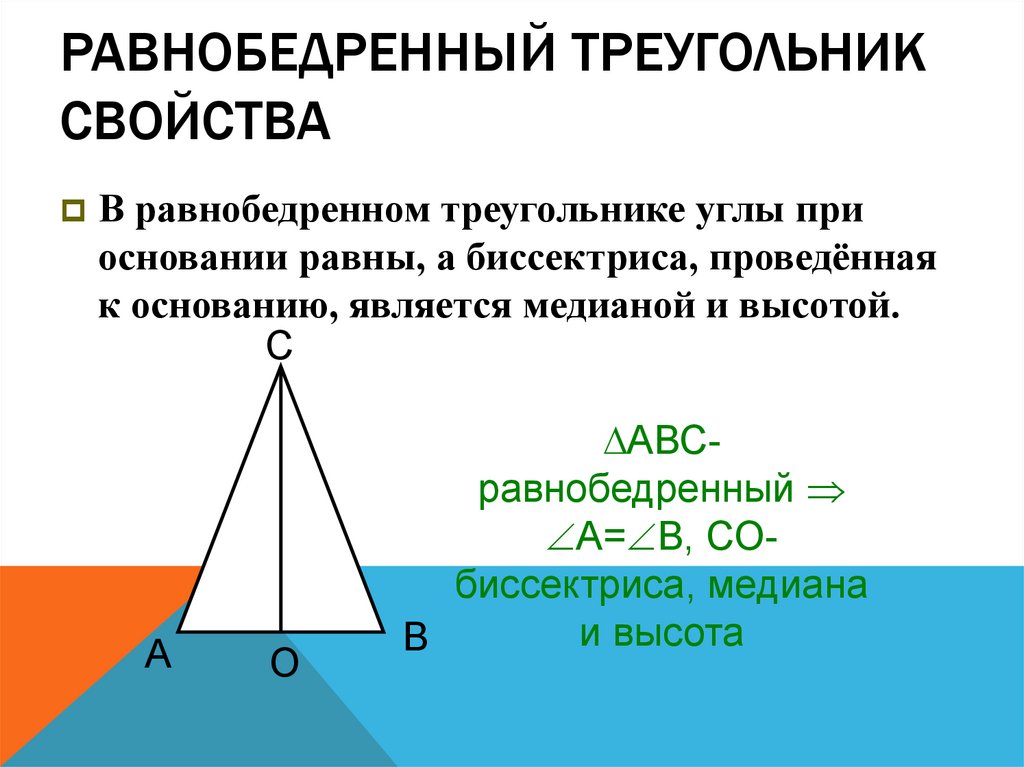
26. Равнобедренный треугольник Свойства
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИКСВОЙСТВА
В равнобедренном треугольнике углы при
основании равны, а биссектриса, проведённая
к основанию, является медианой и высотой.
С
А
О
АВСравнобедренный
А= В, СОбиссектриса, медиана
и высота
В
27. Равнобедренный треугольник Признаки
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИКПРИЗНАКИ
Если в треугольнике два угла равны, то
он равнобедренный.
Если в треугольнике медиана является
высотой, то он равнобедренный.
Если в треугольнике медиана является
биссектрисой, то он равнобедренный.
Если в треугольнике высота является
биссектрисой, то он равнобедренный
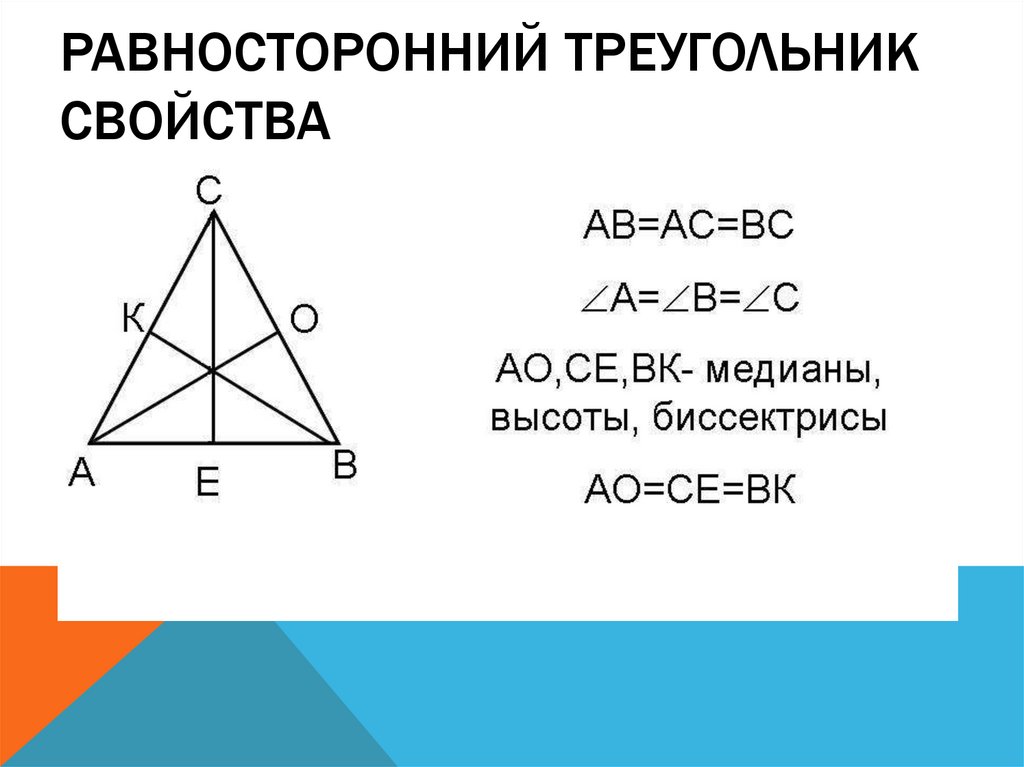
28. Равносторонний треугольник Свойства
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИКСВОЙСТВА
В равностороннем треугольнике все углы равны.
В равностороннем треугольнике каждая биссектриса является медианой и высотой.
В равностороннем треугольнике все три медианы равны.
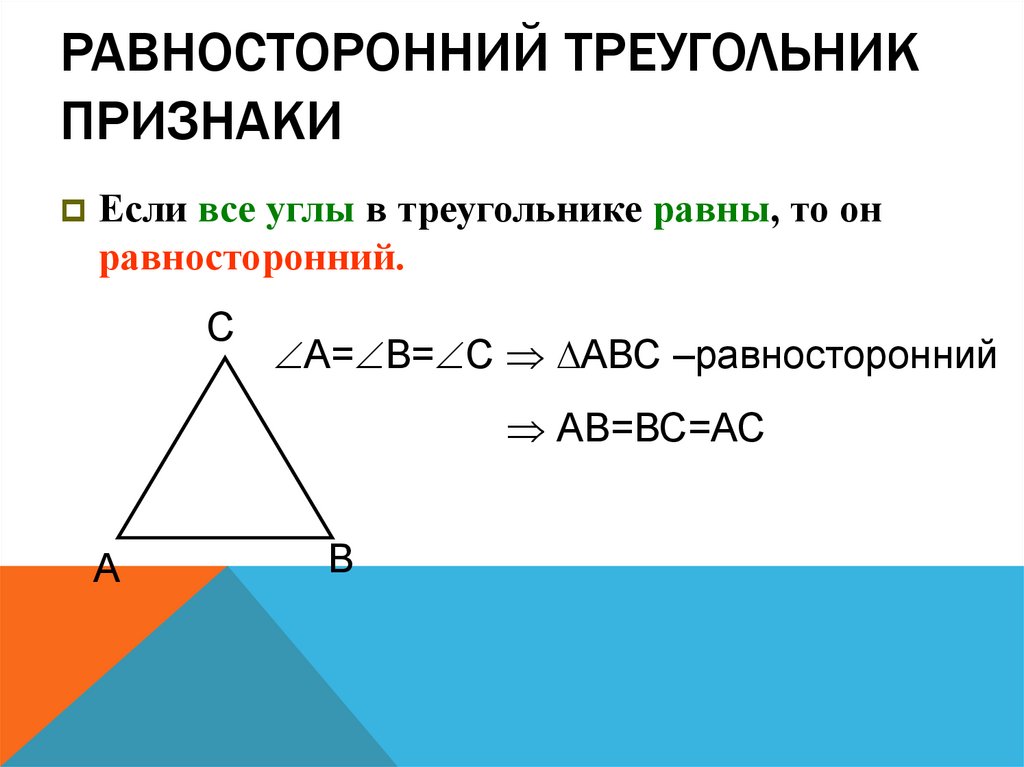
29. Равносторонний треугольник Признаки
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИКПРИЗНАКИ
Если все углы в треугольнике равны, то он
равносторонний.
С
А= В= С АВС –равносторонний
АВ=ВС=АС
А
В
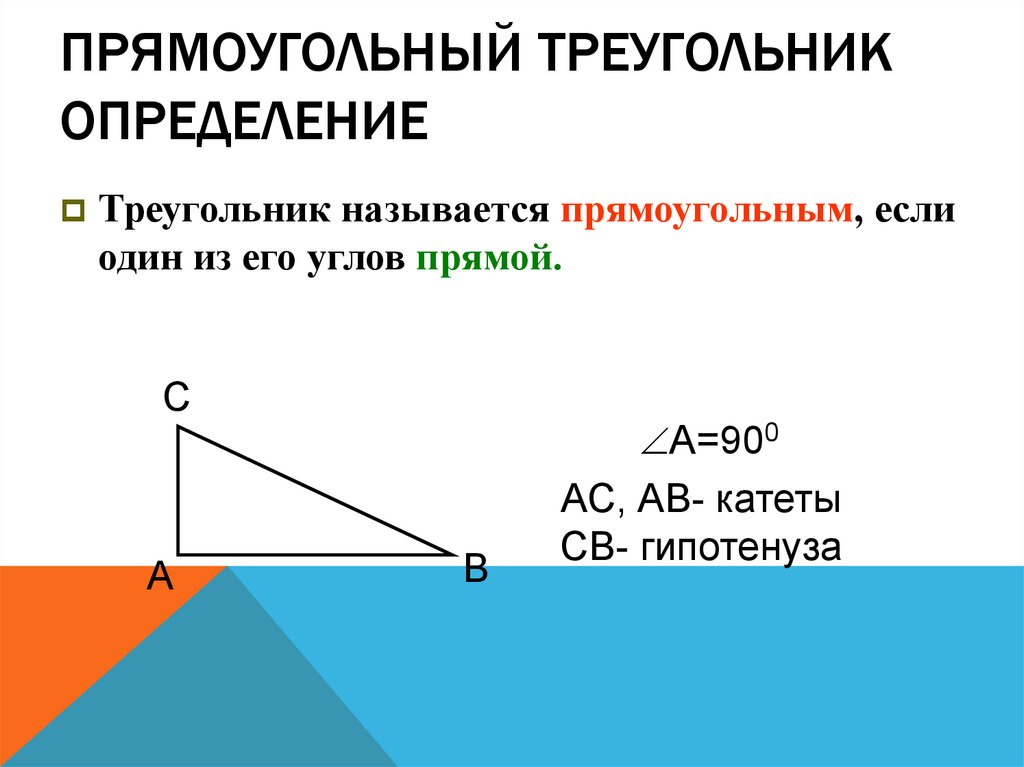
30. Прямоугольный треугольник Определение
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКОПРЕДЕЛЕНИЕ
Треугольник называется прямоугольным, если
один из его углов прямой.
С
А
В
А=900
АС, АВ- катеты
СВ- гипотенуза
31. Прямоугольный треугольник Признаки
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКПРИЗНАКИ
Если катет и гипотенуза одного
прямоугольного треугольника равны катету
катету и гипотенузе другого треугольника,
то такие треугольники равны
32. Прямоугольный треугольник Признаки
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКПРИЗНАКИ
Если два катета одного треугольника
равны двум катетам другого
треугольника,
то такие треугольники равны
33. Прямоугольный треугольник Признаки
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКПРИЗНАКИ
Если катет и острый угол одного
треугольника
равны катету и острому углу
другого треугольника,
то такие треугольники равны
34. Прямоугольный треугольник Признаки
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКПРИЗНАКИ
Если гипотенуза и острый угол одного
треугольника
равны гипотенузе и острому углу другого
треугольника,
то такие треугольники равны
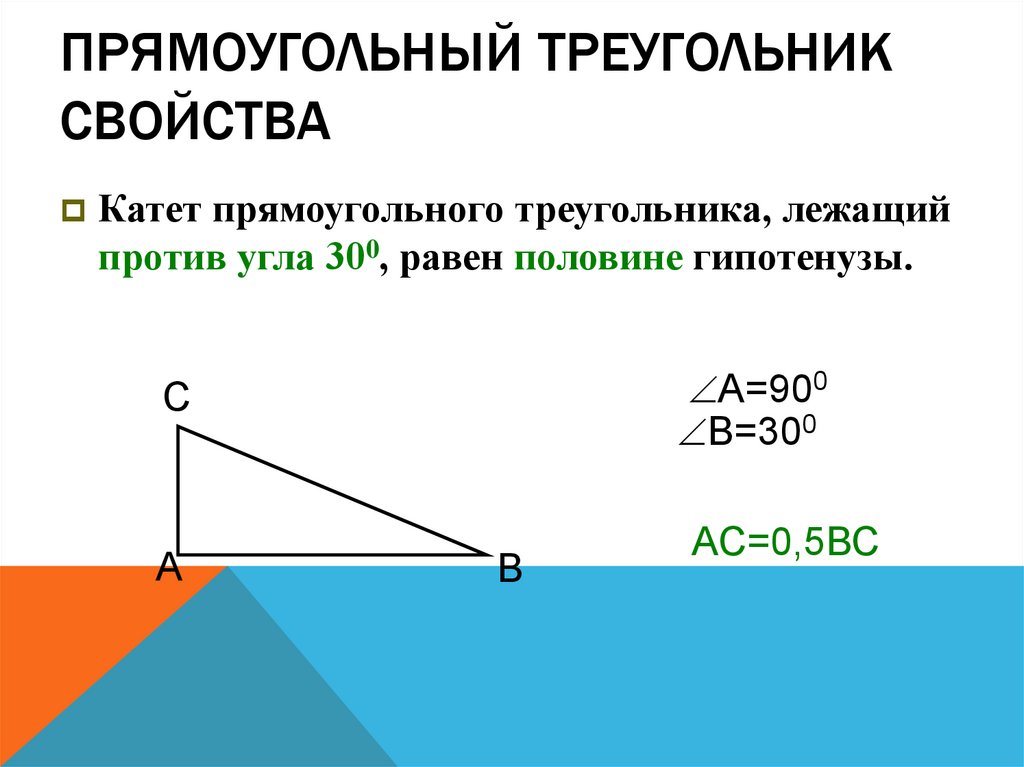
35. Прямоугольный треугольник Свойства
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКСВОЙСТВА
Катет прямоугольного треугольника, лежащий
против угла 300, равен половине гипотенузы.
А=900
В=300
С
А
В
АС=0,5ВС
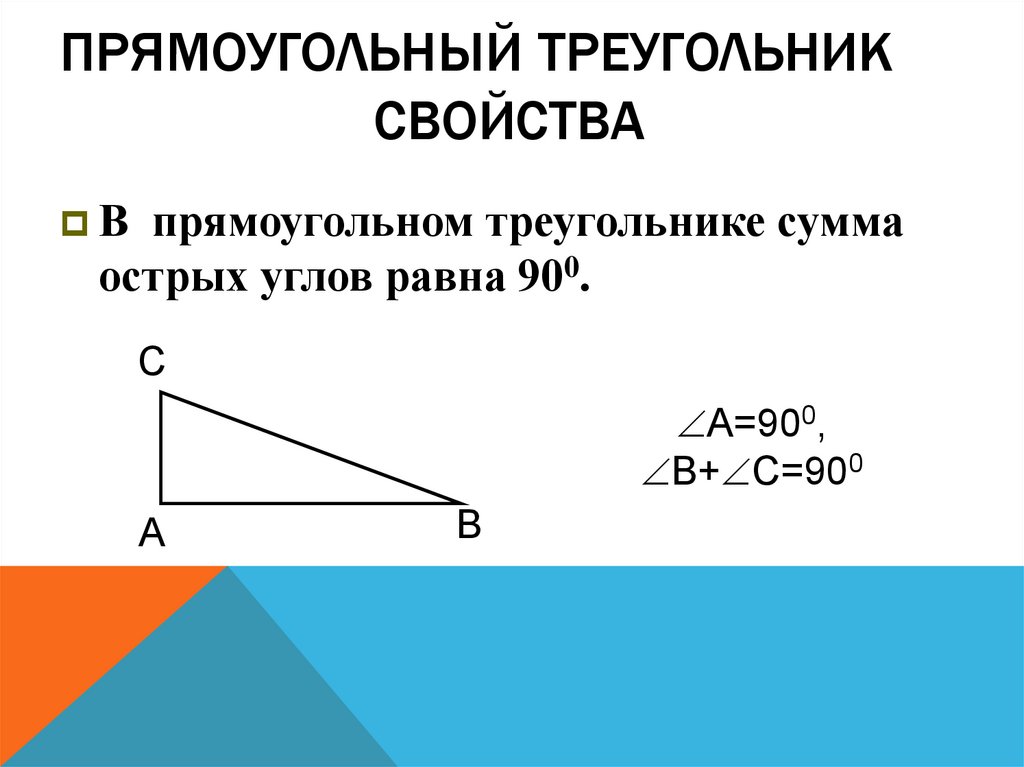
36. Прямоугольный треугольник Свойства
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИКСВОЙСТВА
В прямоугольном треугольнике сумма
острых углов равна 900.
С
А=900,
В+ С=900
А
В












 mathematics
mathematics








