Similar presentations:
Продольно-поперечный изгиб
1.
Продольно-поперечный изгибВ сечениях прямого бруса возникают изгибающие моменты как от
поперечных, так и от продольных сил
2.
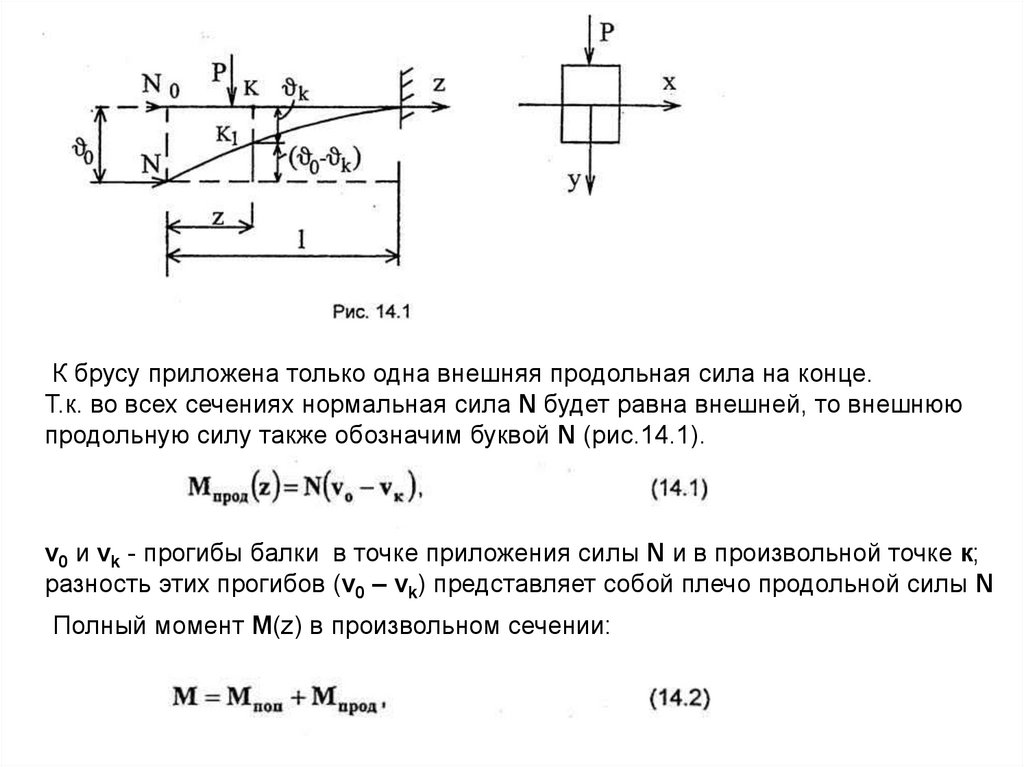
К брусу приложена только одна внешняя продольная сила на конце.Т.к. во всех сечениях нормальная сила N будет равна внешней, то внешнюю
продольную силу также обозначим буквой N (рис.14.1).
v0 и vk - прогибы балки в точке приложения силы N и в произвольной точке к;
разность этих прогибов (v0 – vk) представляет собой плечо продольной силы N
Полный момент M(z) в произвольном сечении:
3.
Дифференциальное уравнение продольно-поперечного изгибаПрогибы v при продольно-поперечном изгибе выражаются через прогибы
при поперечном изгибе vпоп, вычислить которые можно по формуле Мора.
где Рэ – критическая сила (сила Эйлера) равна:
v>vпоп, поскольку продольная сила дополнительно изгибает балку.
С ростом силы N, v возрастают и при N→Рэ ; v→∞.
4.
. Определение краевых напряжений и допускаемой нагрузкиВ сечениях балки при продольно-поперечном изгибе возникают нормальные
напряжения как от продольных, так и от поперечных сил.
Напряжения определяются по формуле:
Подставляя в эту формулу выражение М при продольно – поперечном изгибе:
Эта же формула с учетом приближенного определения прогибов
Максимальные по абсолютному значению напряжения называются краевыми σкраев.
5.
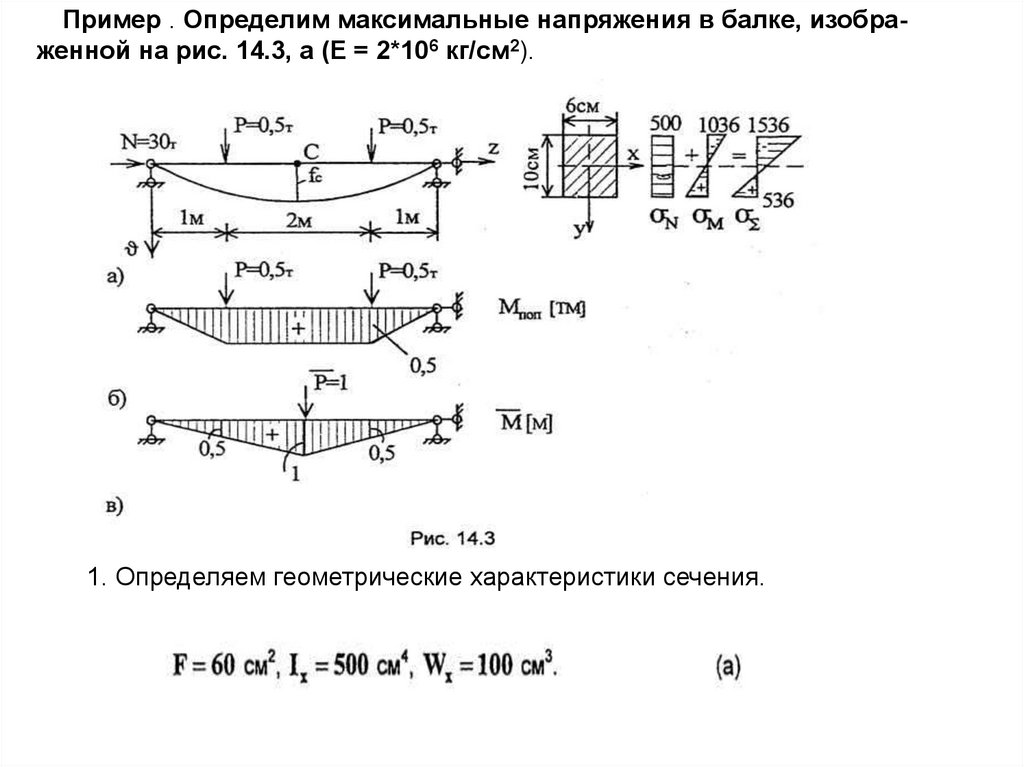
Пример . Определим максимальные напряжения в балке, изображенной на рис. 14.3, а (Е = 2*106 кг/см2).1. Определяем геометрические характеристики сечения.
6.
2. Определяем величину Рэ3.Строим эпюру моментов Мпоп и определяем опасное сечение балки, где
мах Мпоп и vпoп . Это середина балки (рис. 14.3, б); таким образом
4. Определяем прогиб в опасном сечении балки, для чего в этом сечении
прикладываем силу Р = 1, строим соответствующую эпюру моментов М
(рис. 14.3, в) и по формуле Мора вычисляем vc.
5. Вычисляем по формуле (14.17) наибольшие краевые напряжения




 mechanics
mechanics