Similar presentations:
Алгоритми та структури даних. Лекція № 1
1.
Алгоритми таструктури даних
Лекція № 1
доц. Федорченко Володимир
Миколайович
Тел. 073 308 02 40
2.
Cтруктура курсу• Лекції - 20 годин
• Лабораторні роботи - 16 годин (6 Л.Р.)
• Самостійна робота (К) - 12 годин
• Залік
3.
Література4.
Література5.
Література6.
Навіщо вивчати алгоритми таструктури даних?
7.
Алгоритми лежать в основі комп'ютерних наук ірозробки програмного забезпечення.
Реальна продуктивність будь-програмної системи
залежить тільки від двох речей:
•обраного алгоритму
•ефективності його реалізації.
Тому розробка оптимально алгоритму критична
для продуктивності всіх програмних систем. Більш
того, вивчення алгоритмів сприяє вирішенню
проблем незалежно від мови, парадигми
програмування або апаратного забезпечення та
інших аспектів реалізації.
- Computing Curriculum
8.
Algorithms + Data Structures =Programs
Алгоритми + Структури
даних = Програми
Ніклаус Вірт - швейцарський учений, фахівець
в області інформатики, один з найвідоміших
теоретиків в галузі розробки мов
програмування, професор комп'ютерних наук .
9.
Якщо ви вважаєте себе дійсно гарним програмістом..., прочитайте "Мистецтво програмування" (Кнута) ...
Якщо ви зможете прочитати все це, то вам безумовно
слід відправити мені резюме.
- Білл Гейтс.
10.
Витяг з переліку практичнихрезультатів навчання
11.
АтаСДАлгоритм, його властивості.
Види алгоритмів. Форми
запису алгоритмів
12.
Що таке алгоритм?13.
Поняття алгоритмуПоняття «алгоритм» відноситься до числа
найбільш фундаментальних понять
математики, програмування та інформатики.
Запис алгоритму на формальній мові
називається програмою. Іноді саме поняття
алгоритму ототожнюється з його записом,
так що слова «алгоритм» і «програма» майже синоніми.
14.
Алгоритми лежать в основі комп'ютерних наук ірозробки програмного забезпечення.
Реальна продуктивність будь-програмної системи
залежить тільки від двох речей:
•обраного алгоритму
•ефективності його реалізації.
Тому розробка оптимально алгоритму критична
для продуктивності всіх програмних систем. Більш
того, вивчення алгоритмів сприяє вирішенню проблем
незалежно від мови, парадигми програмування або
апаратного забезпечення та інших аспектів реалізації.
- Computing Curriculum
15.
Поняття алгоритмуАлгоритм - це кінцева система правил,
сформульована на мові виконавця, яка визначає
послідовність переходу від допустимих вихідних
даних до кінцевого результату і яка має певні
властивості.
Мухамед бен Муса альХорезмі
(алгоритм - європеїзовані вимова слів
«аль-Хорезмі»)
16.
«Алгоритм - це кінцевий набір правил, який визначає послідовність операцій длявирішення конкретної множини завдань і має п'ять важливих рис: скінченість,
визначеність, введення, виведення, ефективність». (Д. Е. Кнут)
«Алгоритм - це будь-яка система обчислень, яка виконується за строго певними
правилами, яка після будь-якого числа кроків свідомо призводить до вирішення
поставленого завдання». (А. Колмогоров)
«Алгоритм - це точне розпорядження, що визначає обчислювальний процес, що йде
від варійованих вихідних даних до шуканого результату». (А. Марков)
«Алгоритм - точне розпорядження про виконання в певному порядку деякої системи
операцій, що ведуть до розв'язання всіх завдань даного типу». (Філософський
словник / За ред. М. М. Розенталя)
«Алгоритм - строго детермінована послідовність дій, що описує процес
перетворення об'єкта з початкового стану в кінцевий, записана за допомогою
зрозумілих виконавцю команд». (Микола Дмитрович Угринович, підручник
«Інформатика і інформ. технології»)
«Алгоритм - це послідовність дій, спрямованих на отримання певного результату за
кінцеве число кроків».
17.
Інтуїтивне поняття алгоритмуНаведіть приклади алгоритмів
(математичних і нематематичних)
1) Алгоритм додавання двох довільних
натуральних чисел, записаних в десятковій
системі числення
2) Алгоритм приготування манної каші
3) Піди туди, не знаю куди, принеси те, не знаю
що
18.
Походження слова алгоритмІсторична довідка
Походження слова алгоритм пов'язане з
алгоритмами позиційної арифметики
Правила з числами, записаними в десятковій системі
числення, були вперше знайдені в середньовічній
Індії
19.
Походження слова алгоритмІсторична довідка
Європейці познайомилися з ними
по книзі арабського вченого IX століття
Мухаммеда ібн Муса аль-Хорезмі, що буквально означає
«Мухаммед син Муси, уродженець Хорезма »
В ті часи Аральське море називалося «озером Хорезм», а саме
місто Хорезм розташовувалося на південь від цього моря в
басейні річки Амудар’ї
Ім'я вченого аль-Хорезмі латинізованого і стало звучати
«алхорізм»,«алгорифм»,«алгоритм»
20.
Поняття, пов'язані з поняттям алгоритму- Кожен алгоритм має виконавця (пристрій або людина, яка
виконує алгоритм)
- Алгоритм задає обчислювальний (алгоритмічний) процес,
який складається з окремих, елементарних кроків - тактів
алгоритму
- Алгоритм переробляє початковий набір даних Р (Вхідний
об'єкт) в результат роботи Q (Об'єкт на виході)
- Кожен такт роботи алгоритму завершується переходом в
новий стан, серед яких деякі орієнтуються як заключні стани
21.
Алгоритм повинен відповідати певним вимогам.Прийнято виділяти наступні вимоги:
1.
2.
3.
4.
5.
6.
7.
Наявність введення вихідних даних.
Наявність виведення результату виконання.
Однозначність (комп'ютер «розуміє» тільки
однозначні інструкції).
Загальність - алгоритм призначений для вирішення
певного класу задач.
Коректність - алгоритм повинен давати правильне
рішення завдання.
Скінченність - рішення задачі повинно бути отримано
за кінцеве число кроків.
Ефективність - для вирішення завдання повинні
використовуватися обмежені ресурси комп'ютера
(процесорний час, обсяг оперативної пам'яті і т.д.).
22.
Властивості алгоритму:Масовість - алгоритм повинен описувати коло однотипних
завдань, вихідні дані яких можуть змінюватися в певних
межах.
Детермінованість - при кожному запуску алгоритму з
одними і тими ж вихідними даними повинен бути
отриманий один і той же результат
Зрозумілість – дії або кроки алгоритму повинні бути
сформульовані так, щоб вони були сприйняті однаково
розробником і виконавцем, тобто вони повинні бути
однозначно зрозумілі.
Дискретність - чіткий розподіл всього шляху вирішення
завдання на окремі етапи (кроки) так, щоб хід виконання
алгоритму проходив поетапно, вчасно коригуючи дії
виконавця.
Результативність - точне виконання розпоряджень
алгоритму має привести до результату за n кроків, якщо
правильно розроблена вихідна модель і сам алгоритм.
23.
Властивості алгоритмуМасовість - алгоритм правильно працює на
деякій множині вихідних даних (область
застосовності алгоритму), тобто алгоритм
придатний для вирішення будь-якої задачі з
деякого класу задач.
Цю властивість не слід
розуміти як можливість
вирішити багато завдань.
24.
Властивості алгоритмівДетермінованість - на кожному кроці
однозначно визначено перетворення об'єктів
середовища
виконавця,
отриманого
на
попередніх етапах алгоритму.
Ця властивість об'єднує в собі
одночасне виконання
властивостей точності і
зрозумілості.
25.
Властивості алгоритмівДискретність - розбиття виконання алгоритму
на послідовність закінчених дій-кроків, і кожна
дія має бути закінчена виконавцем перш, ніж
він приступить до виконання наступної дії.
Кожну окрему дію виконавцю
наказує спеціальна вказівка команда.
26.
Властивості алгоритмівРезультативність - кожен крок після свого
завершення дає середовище, в якій всі об'єкти
однозначно визначені.
Це властивість вимагає,
щоб в алгоритмі не було
помилок.
27.
Зображувальні засоби для опису (подання)алгоритму
Для запису алгоритму розв'язання задачі
застосовуються наступні зображувальні способи
їх подання:
Словесно-формульний опис
Графічний спосіб (блок-схема (схема
алгоритму, схема графічних символів), Flowформи, діаграми Нассі-Шнейдермана)
Алгоритмічні мови
Операційні схеми
Псевдокод
28.
Для запису алгоритму існує загальнаметодика:
Кожен алгоритм повинен мати ім'я, яке
розкриває його сенс.
Необхідно позначити початок і кінець
алгоритму.
Описати вхідні і вихідні дані.
Вказати команди, які дозволяють
виконувати певні дії над виділеними
даними
29.
Формульно-словесний спосіб записуалгоритму характеризується тим, що
опис здійснюється за допомогою слів
і формул. Зміст послідовності етапів
виконання алгоритмів записується
природною професійною мовою
предметної області в довільній
формі.
30.
Графічний спосібГрафічний спосіб (схема алгоритму)
представлення алгоритмів є більш
компактним і наочним порівняно з
словесним.
При графічному поданні алгоритм
зображується у вигляді послідовності
пов'язаних між собою функціональних
блоків, кожен з яких відповідає виконанню
однієї або декількох дій.
Таке графічне представлення називається
схемою алгоритму або блок-схемою.
31.
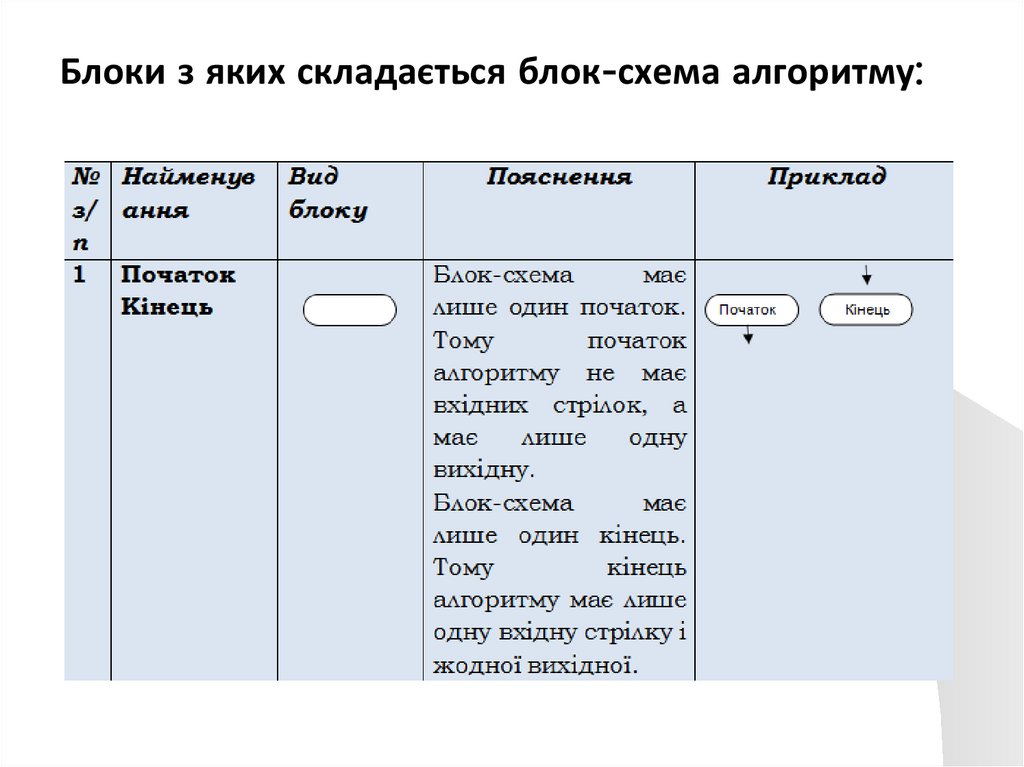
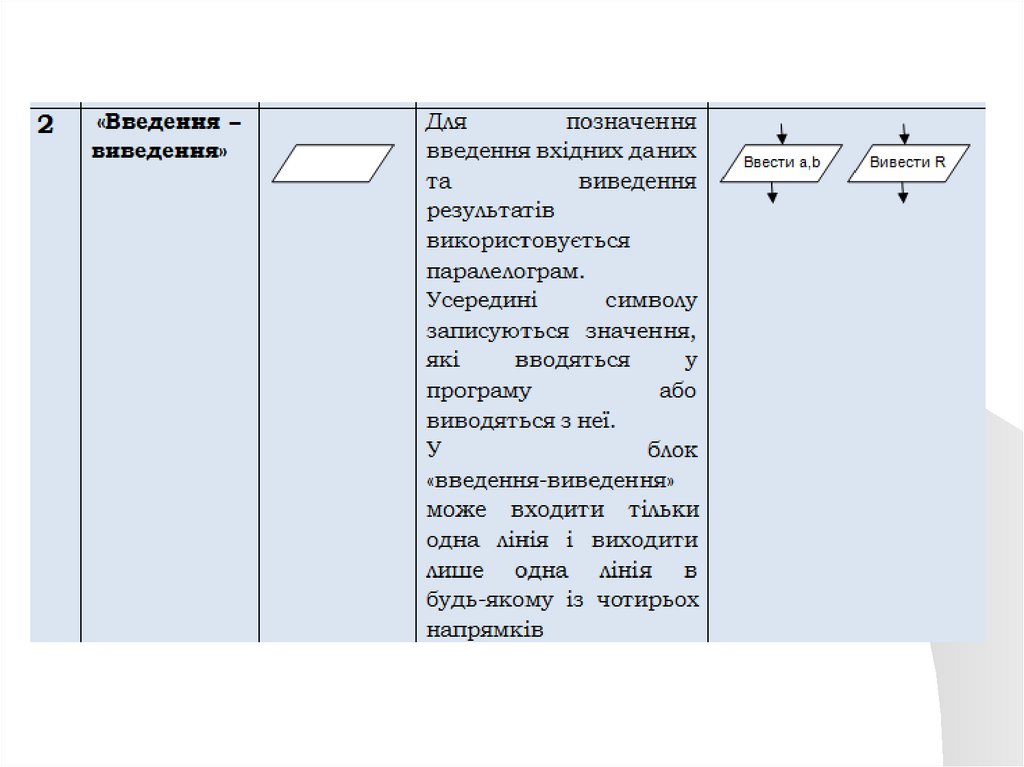
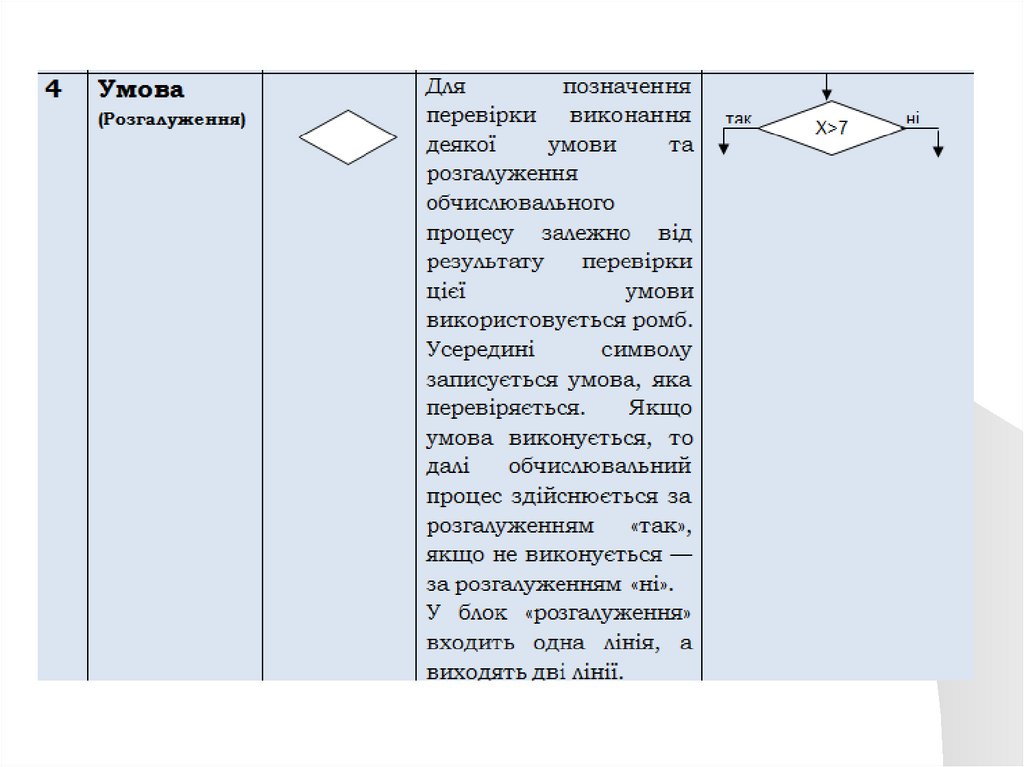
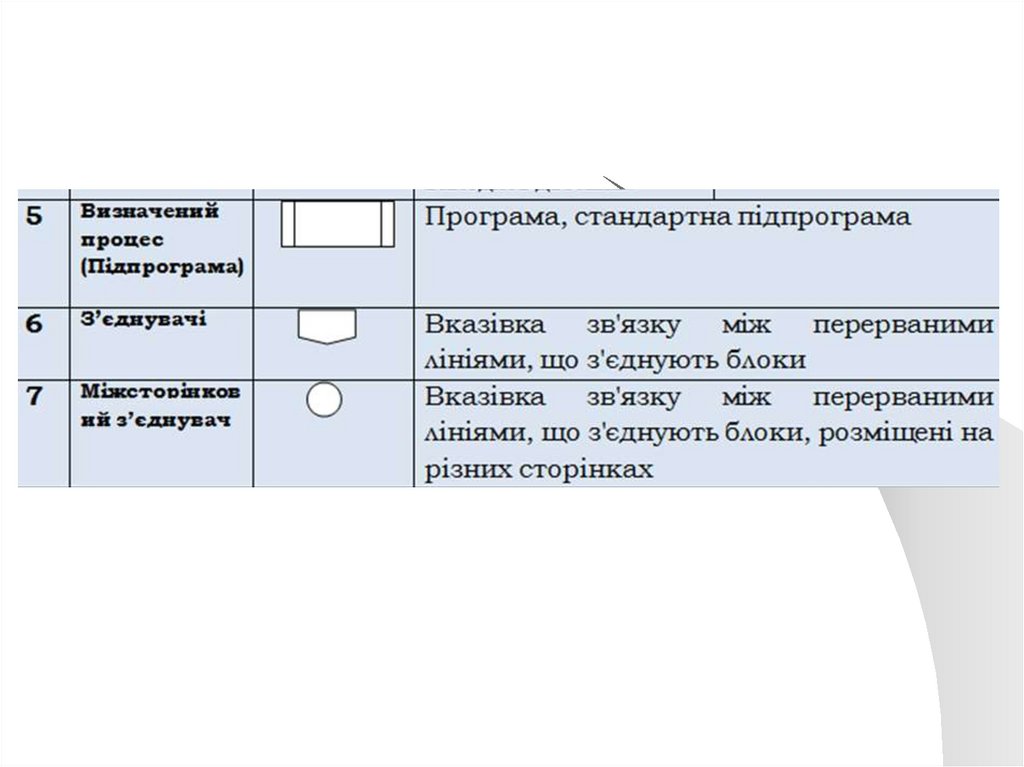
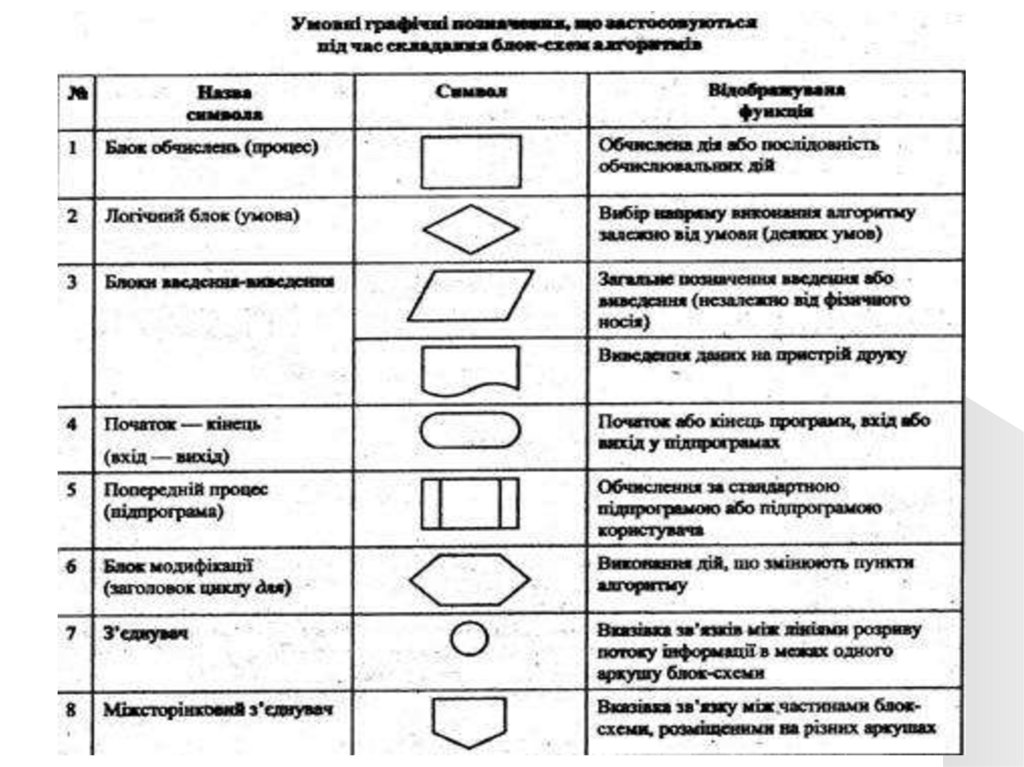
Блок-схемаУ блок-схемі кожному типу дій (введення
вихідних даних, обчислення значень виразів,
перевірці умов, керування повторенням дій,
закінчення обробки і т.п.) відповідає
геометрична фігура, представлена у вигляді
блочного
символу.
Блокові
символи
з'єднуються лініями переходів (лінія або
стрілка),
що
визначають
черговість
виконання дій.
Для
зображення
схем
алгоритмів
розроблений ГОСТ 19.701-90
32.
Блоки з яких складається блок-схема алгоритму:33.
34.
35.
36.
37.
38.
Алгоритмічні конструкції39.
Підчас конструювання алгоритмів
усі операції можна подати у вигляді
комбінацій трьох типів операцій, так
званих
базових
алгоритмічних
структур.
Базові алгоритмічні конструкції
(керівної структури) - способи
керування
процесами
обробки
даних.
40.
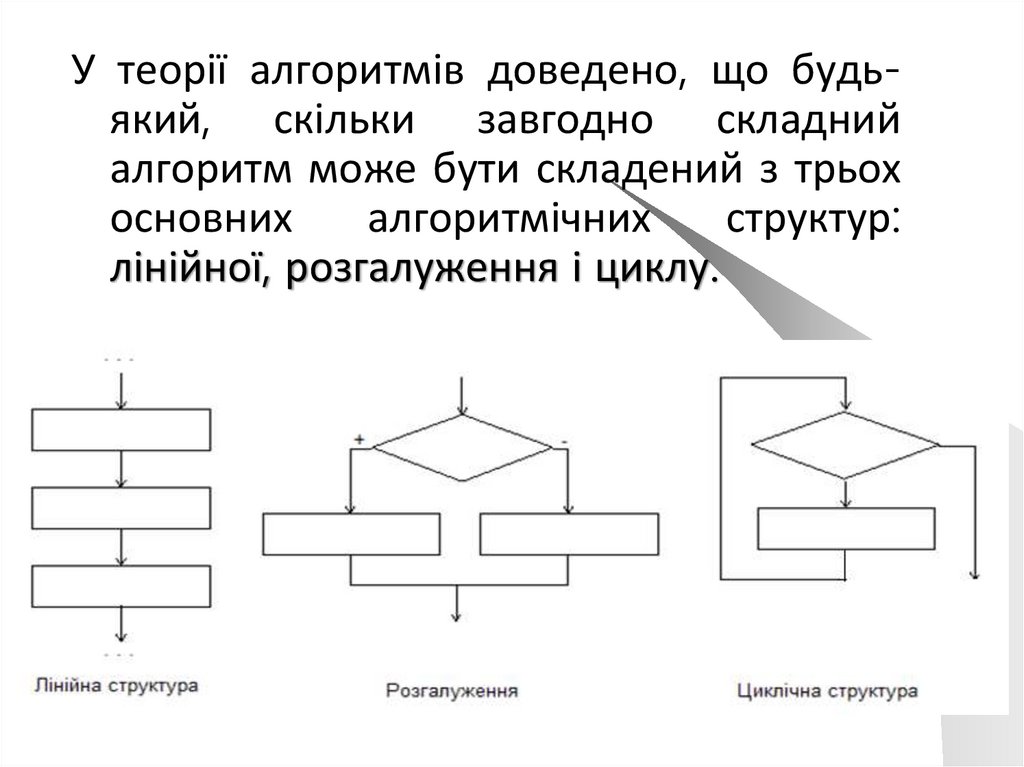
У теорії алгоритмів доведено, що будьякий, скільки завгодно складнийалгоритм може бути складений з трьох
основних
алгоритмічних
структур:
лінійної, розгалуження і циклу.
41.
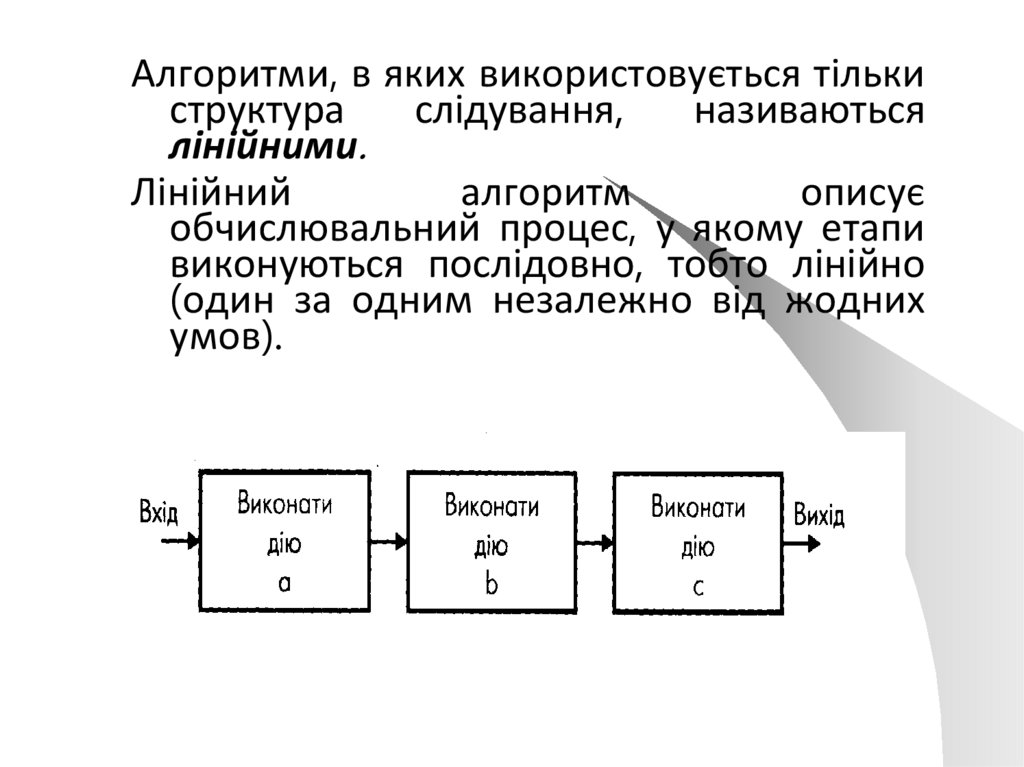
Алгоритми, в яких використовується тількиструктура
слідування,
називаються
лінійними.
Лінійний
алгоритм
описує
обчислювальний процес, у якому етапи
виконуються послідовно, тобто лінійно
(один за одним незалежно від жодних
умов).
42.
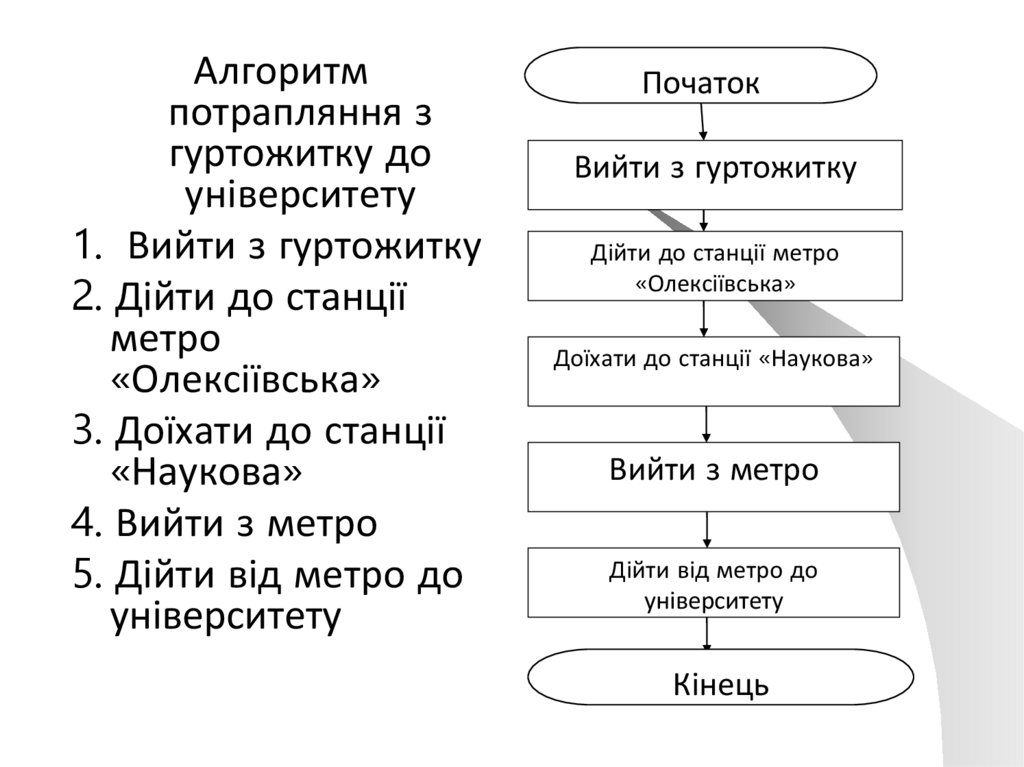
Алгоритмпотрапляння з
гуртожитку до
університету
1. Вийти з гуртожитку
2. Дійти до станції
метро
«Олексіївська»
3. Доїхати до станції
«Наукова»
4. Вийти з метро
5. Дійти від метро до
університету
Початок
Вийти з гуртожитку
Дійти до станції метро
«Олексіївська»
Доїхати до станції «Наукова»
Вийти з метро
Дійти від метро до
університету
Кінець
43.
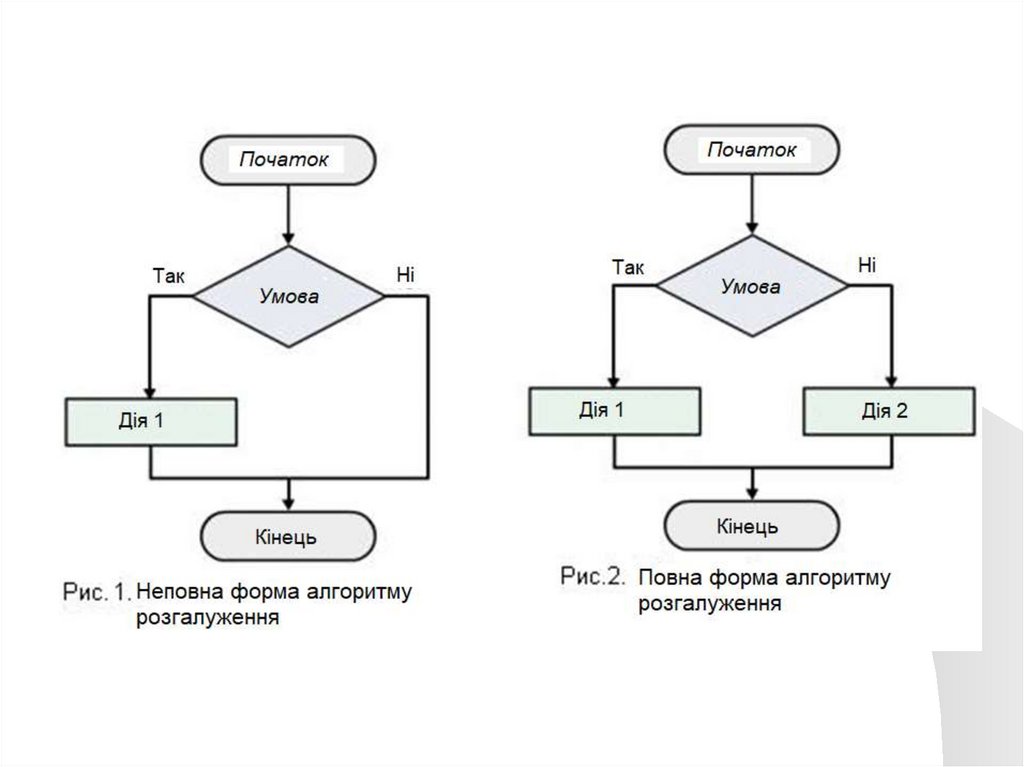
Алгоритми, в основі яких лежить структурарозгалуження, називаються розгалуженими.
Такий алгоритм описує обчислювальний процес, у
якому порядок обчислень залежить від вихідних
умов або від проміжних результатів. Розгалужений
алгоритм виконується по одному з кількох,
заздалегідь
передбачених
напрямків,
які
називаються гілками. У кожному конкретному
випадку процес реалізується тільки по одній гілці,
тобто виконується одна або інша послідовність дій
залежно від того, істинною чи хибною в певний
момент є умова, що перевіряється.
Є дві форми запису розгалужень — повна й
неповна.
44.
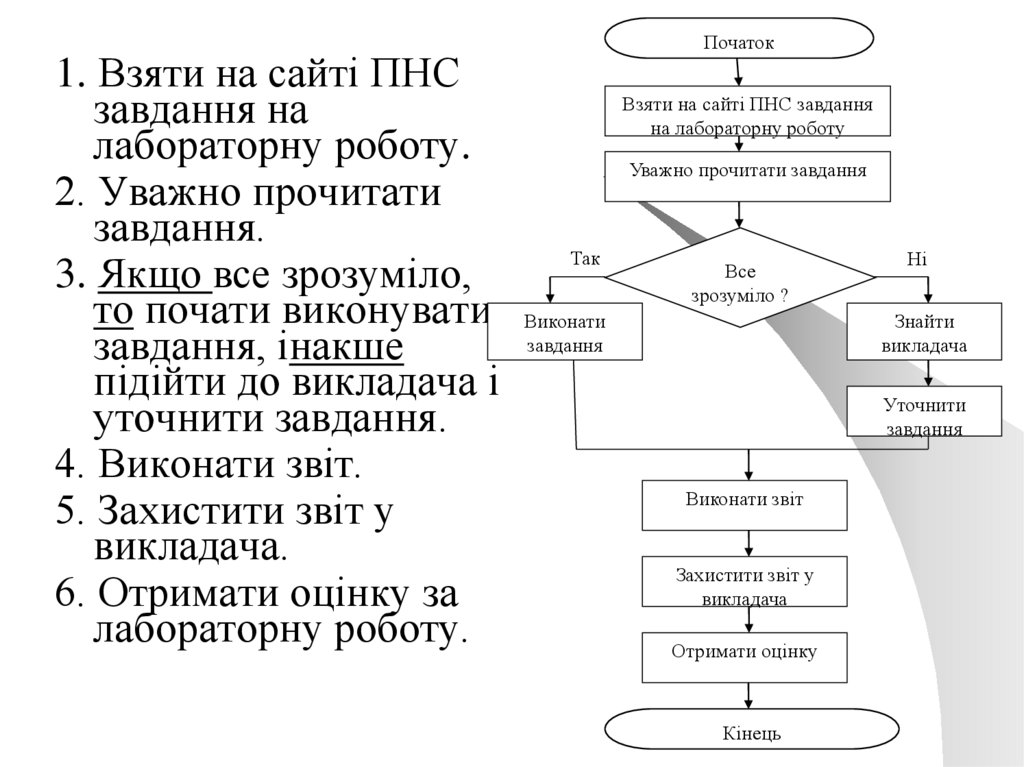
45.
Початок1. Взяти на сайті ПНС
Взяти на сайті ПНС завдання
завдання на
на лабораторну роботу
лабораторну роботу.
Уважно прочитати завдання
2. Уважно прочитати
завдання.
Так
Ні
Все
3. Якщо все зрозуміло,
зрозуміло ?
то почати виконувати Виконати
Знайти
завдання
викладача
завдання, інакше
підійти до викладача і
Уточнити
уточнити завдання.
завдання
4. Виконати звіт.
Виконати звіт
5. Захистити звіт у
викладача.
Захистити звіт у
викладача
6. Отримати оцінку за
лабораторну роботу.
Отримати оцінку
Кінець
46.
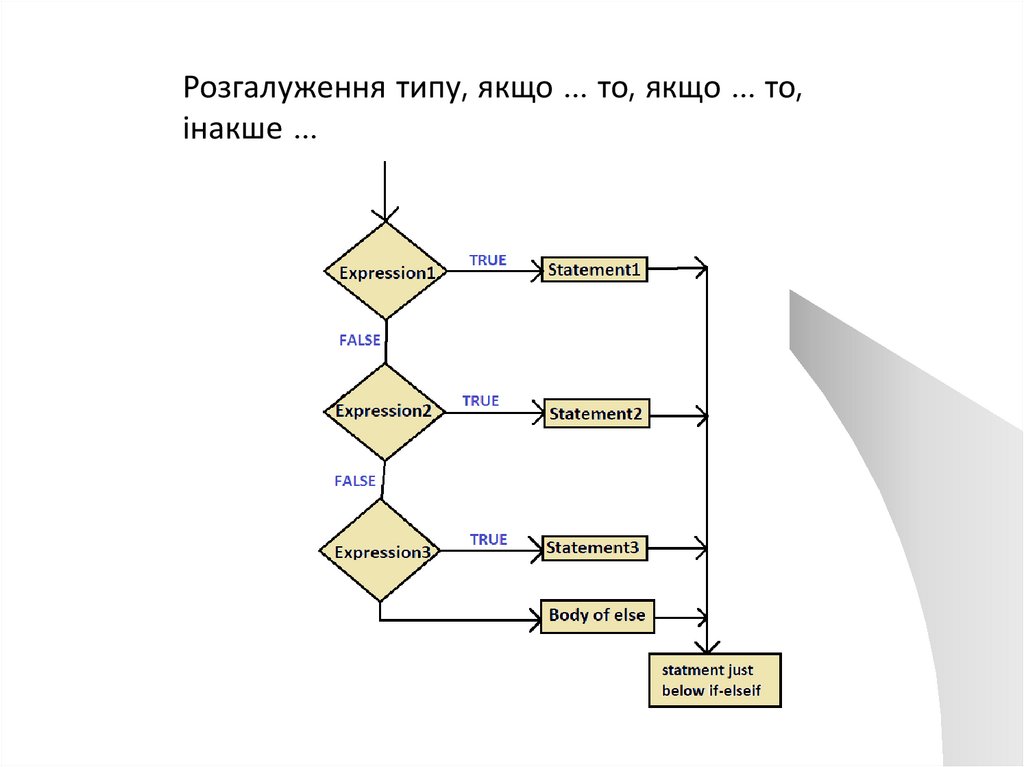
Розгалуження типу, якщо … то, якщо … то,інакше …
47.
Алгоритми,в основі яких лежить
структура повторення, називаються
циклічними.
Циклічний
алгоритм
описує
обчислювальний процес, що містить
однотипні, багаторазово повторювані
послідовності команд.
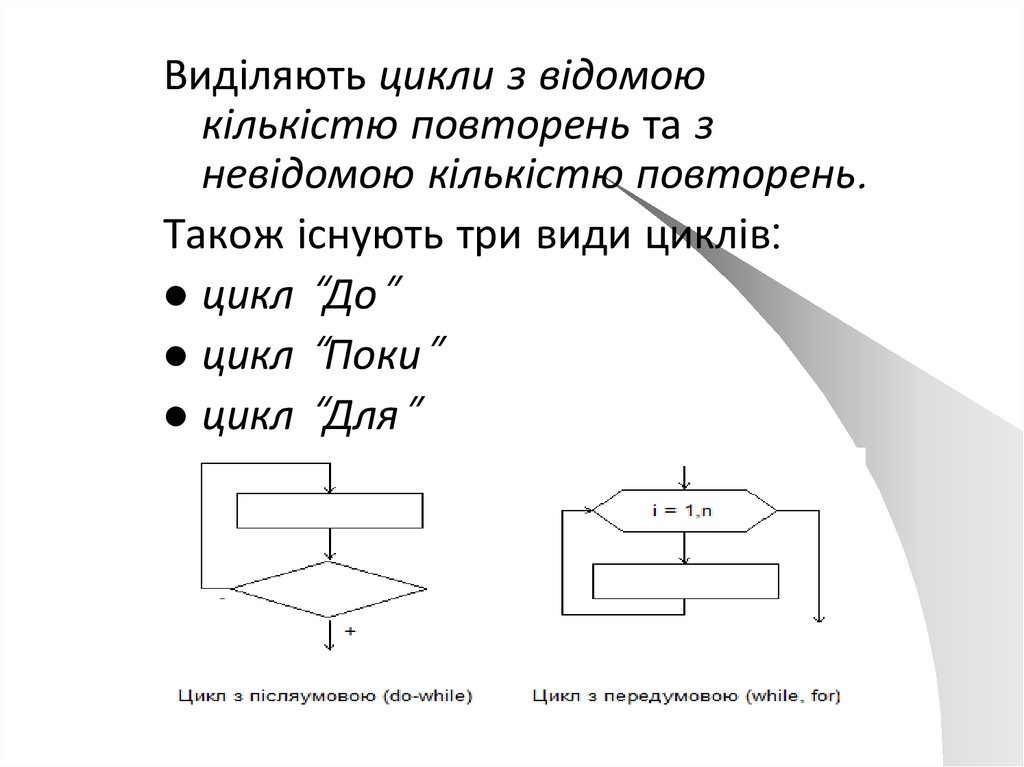
48.
Виділяють цикли з відомоюкількістю повторень та з
невідомою кількістю повторень.
Також існують три види циклів:
цикл “До”
цикл “Поки”
цикл “Для”
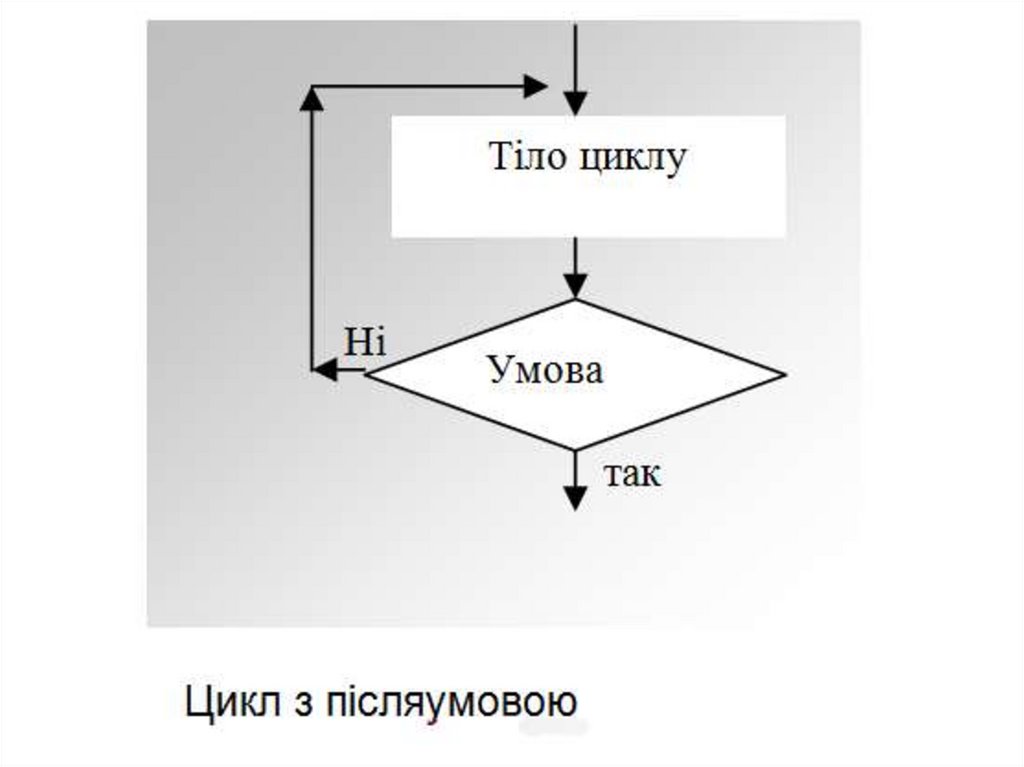
49.
50.
51.
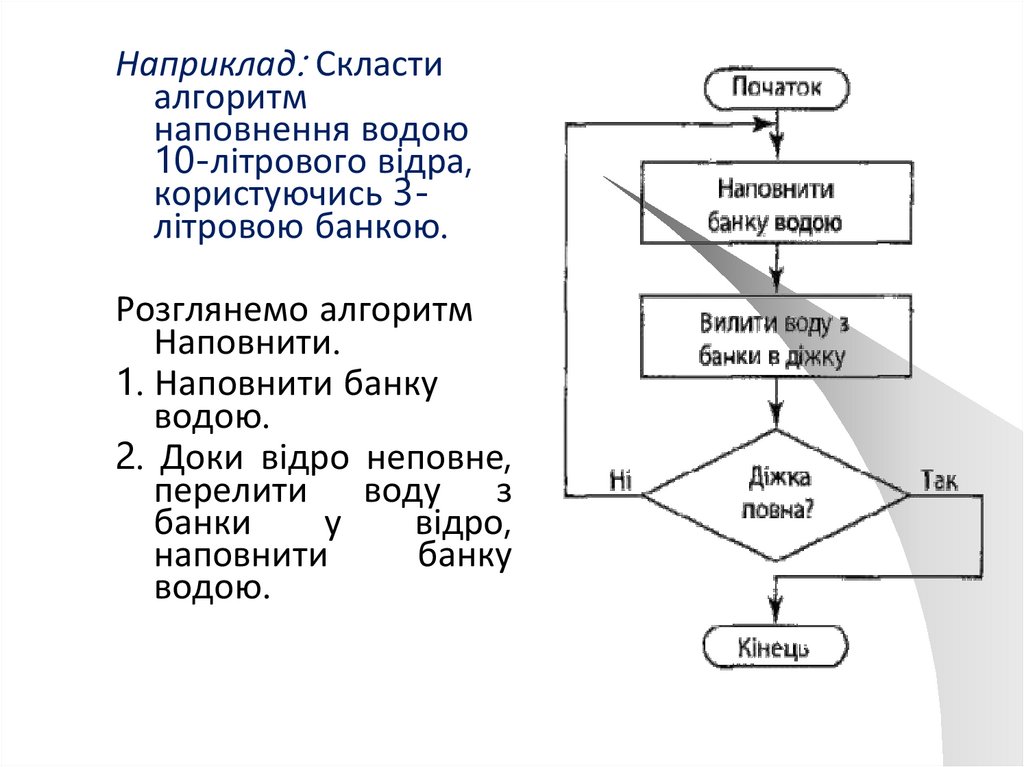
Наприклад: Скластиалгоритм
наповнення водою
10-літрового відра,
користуючись 3літровою банкою.
Розглянемо алгоритм
Наповнити.
1. Наповнити банку
водою.
2. Доки відро неповне,
перелити воду з
банки
у
відро,
наповнити
банку
водою.
52.
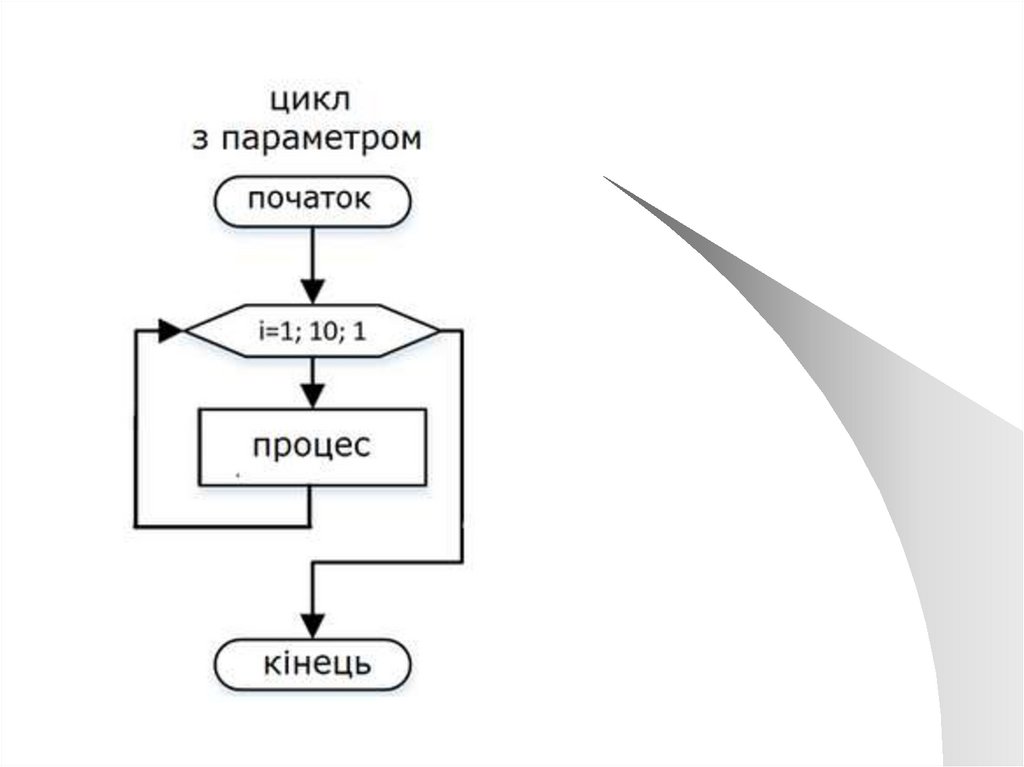
Цикл із заданою кількістю повторень тілациклу (В мовах програмування його
називають "цикл з параметром" або "цикл
з лічильником") - це теж цикл з
передумовою. Дії повторюються певну
кількість разів і відраховуютьсяперед
кожним виконанням.
53.
54.
55.
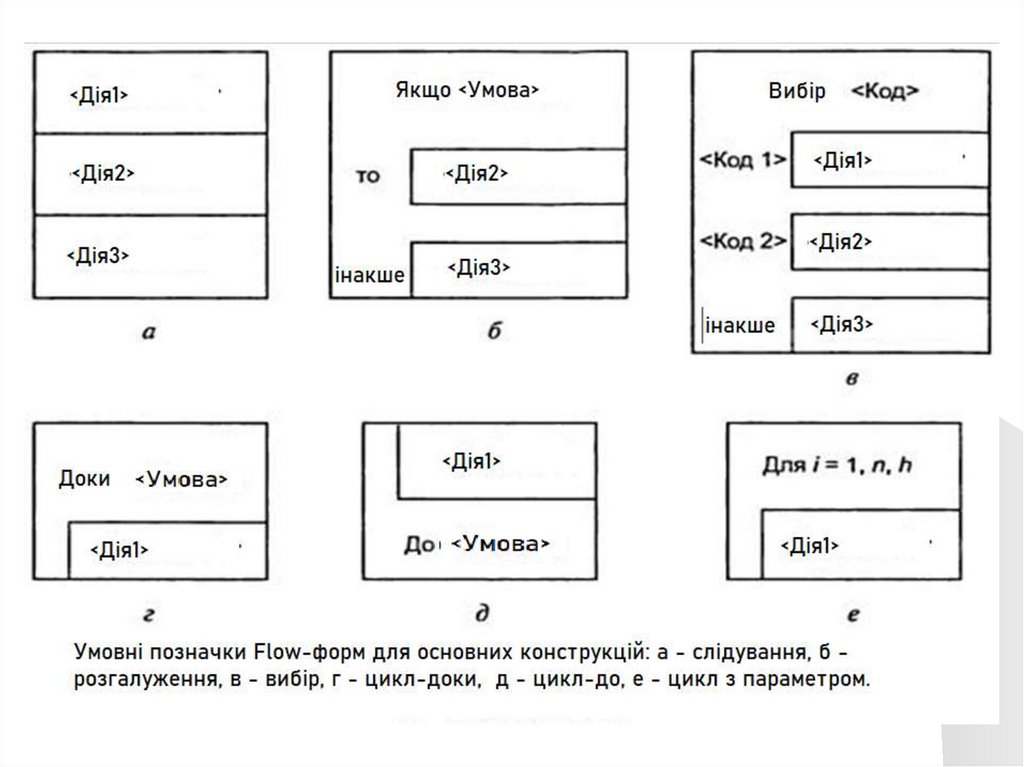
Flow-формиFlow-форми представляють собою графічну
нотацію опису структурних алгоритмів, яка
ілюструє вкладеність структур. Кожен
символ
Flow-форми
має
вигляд
прямокутника і може бути вписана в
будь-який внутрішній прямокутник будьякого іншого символу. Нотація Flow-форм
приведена на наступному слайді.
56.
57.
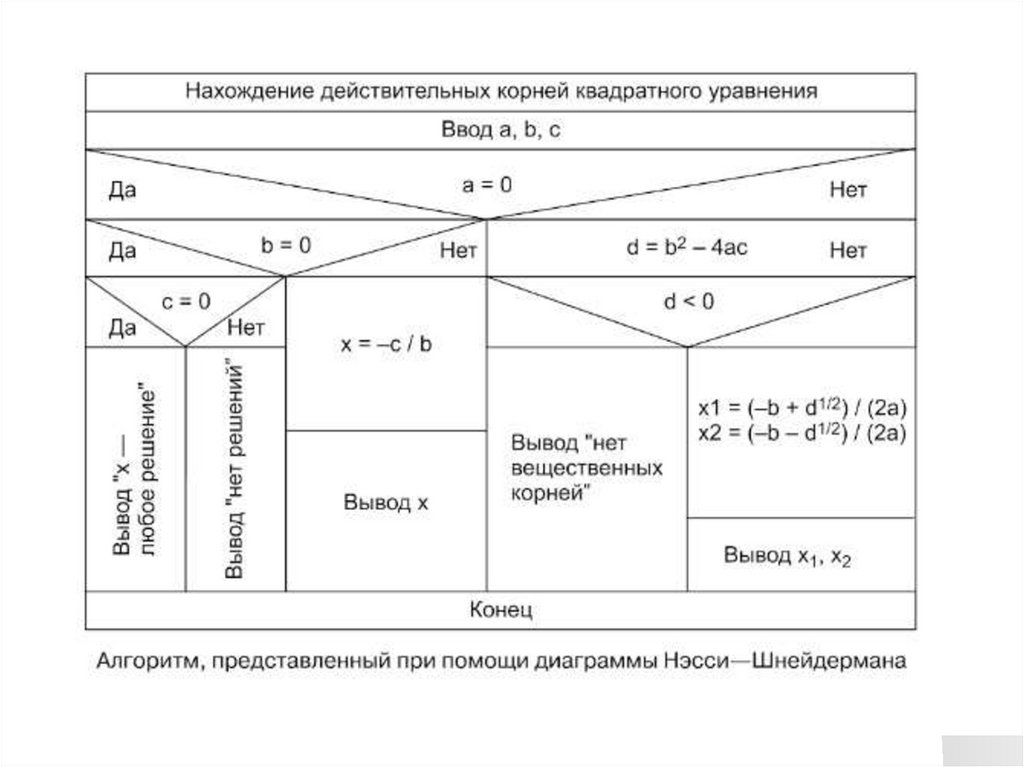
Діаграми Нассі-ШнейдерманаЗапис є більш компактним.
Зобразивши алгоритм або програму у вигляді
діаграми Нассі - Шнейдермана, можна бути
гарантовано впевненим в тому, що принципи
структурного програмування дотримані.
Діаграми Нассі - Шнейдермана зручніше
використовувати для покрокової деталізації
завдання, так як вони теж будуються за
принципом покрокової деталізації - спочатку
діаграма являє собою один прямокутник, потім в
ньому малюється деяка структура управління, в
якій є кілька прямокутників, і далі з кожним
прямокутником може бути виконана та ж
операція.
58.
Діаграми Нассі-Шнейдермананаочність;
відсутність сполучних ліній зі стрілками, що
допомагає уникнути випадкових помилок;
простота використання.
Загальним недоліком Flow-форм і діаграм
Нассі -Шнейдермана є складність побудови
зображень символів, що ускладнює практичне
застосування цих нотацій для опису великих
алгоритмів.
59.
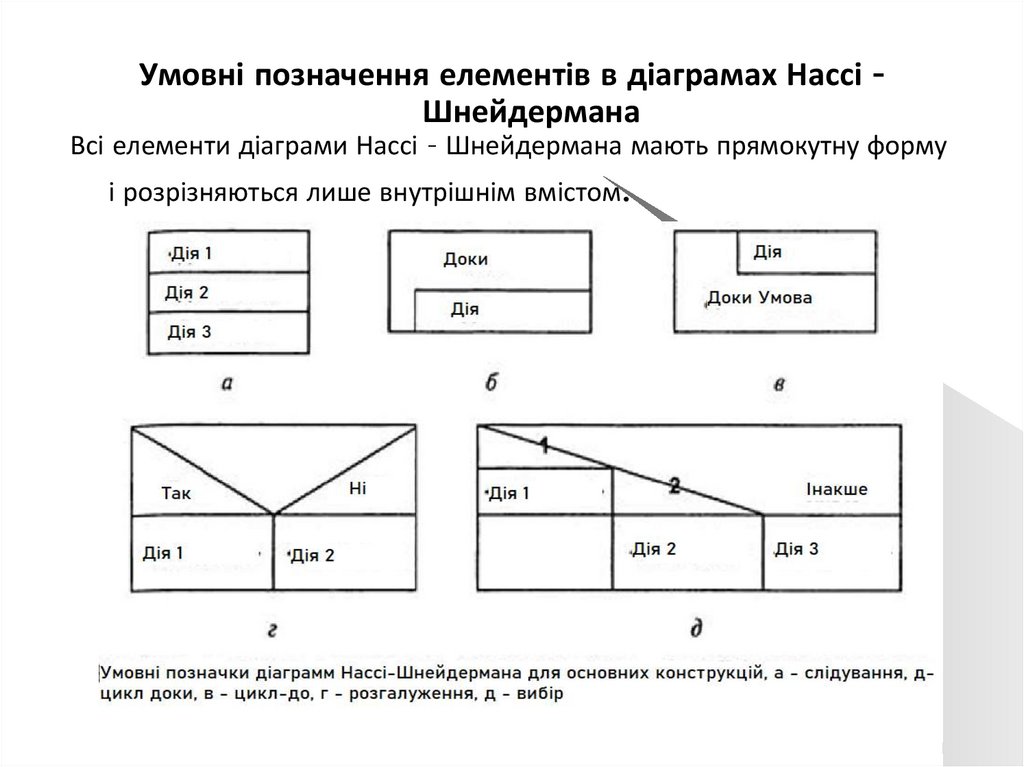
Умовні позначення елементів в діаграмах Нассі ШнейдерманаВсі елементи діаграми Нассі - Шнейдермана мають прямокутну форму
і розрізняються лише внутрішнім вмістом.
60.
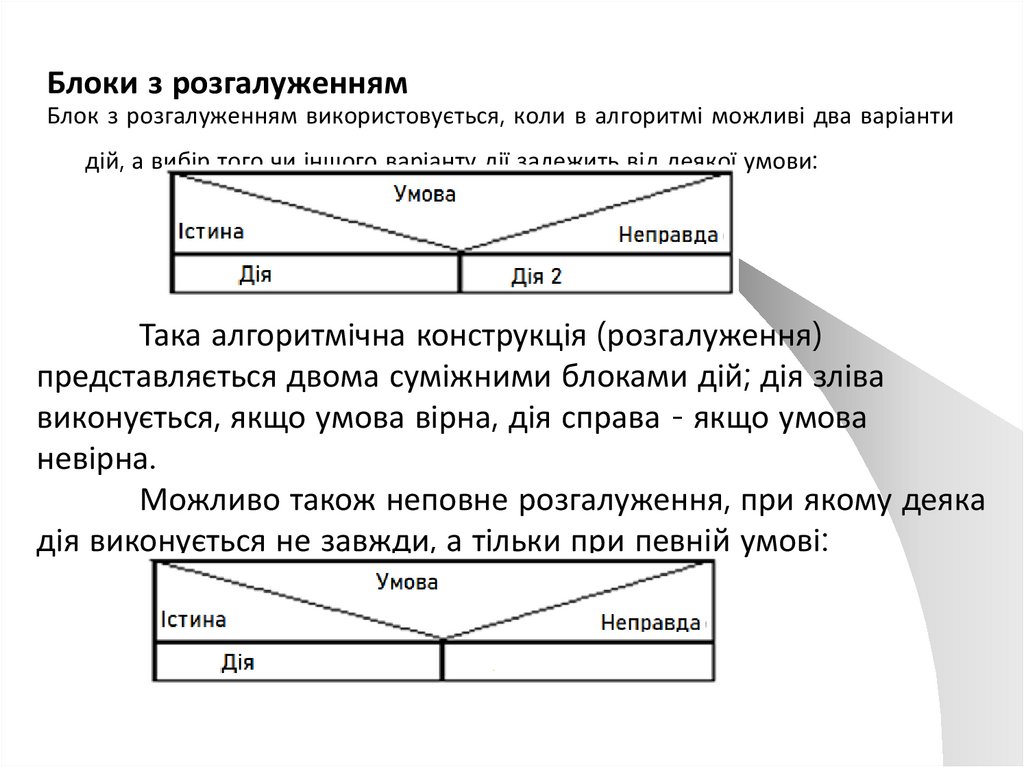
Блоки з розгалуженнямБлок з розгалуженням використовується, коли в алгоритмі можливі два варіанти
дій, а вибір того чи іншого варіанту дії залежить від деякої умови:
Така алгоритмічна конструкція (розгалуження)
представляється двома суміжними блоками дій; дія зліва
виконується, якщо умова вірна, дія справа - якщо умова
невірна.
Можливо також неповне розгалуження, при якому деяка
дія виконується не завжди, а тільки при певній умові:
61.
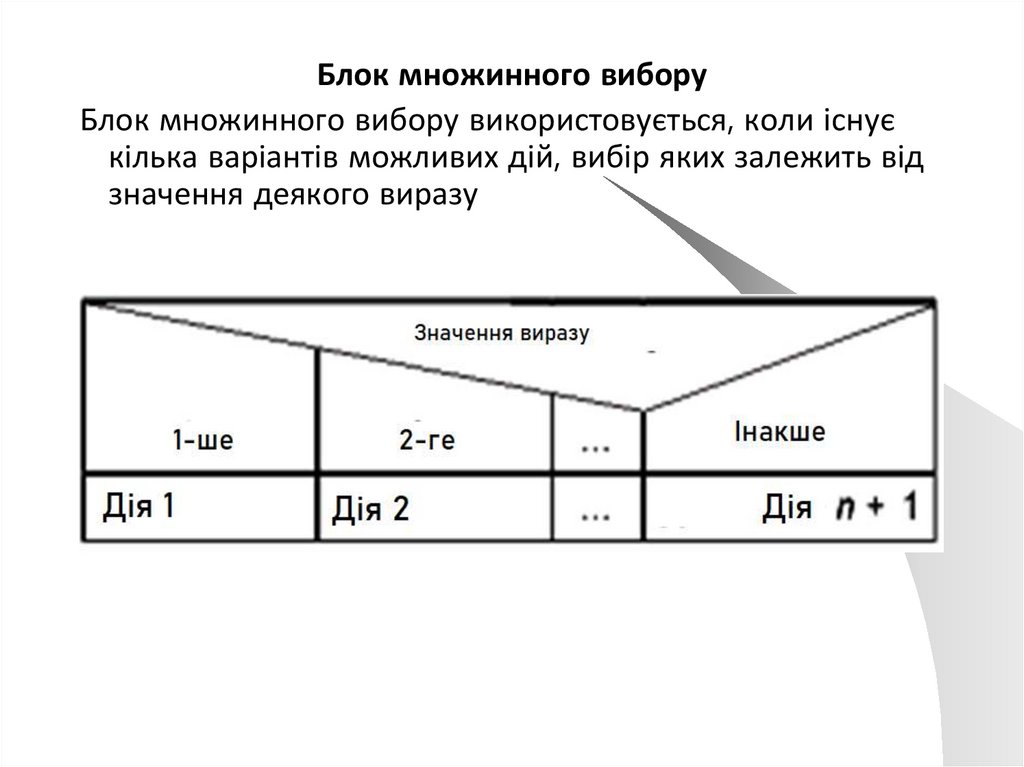
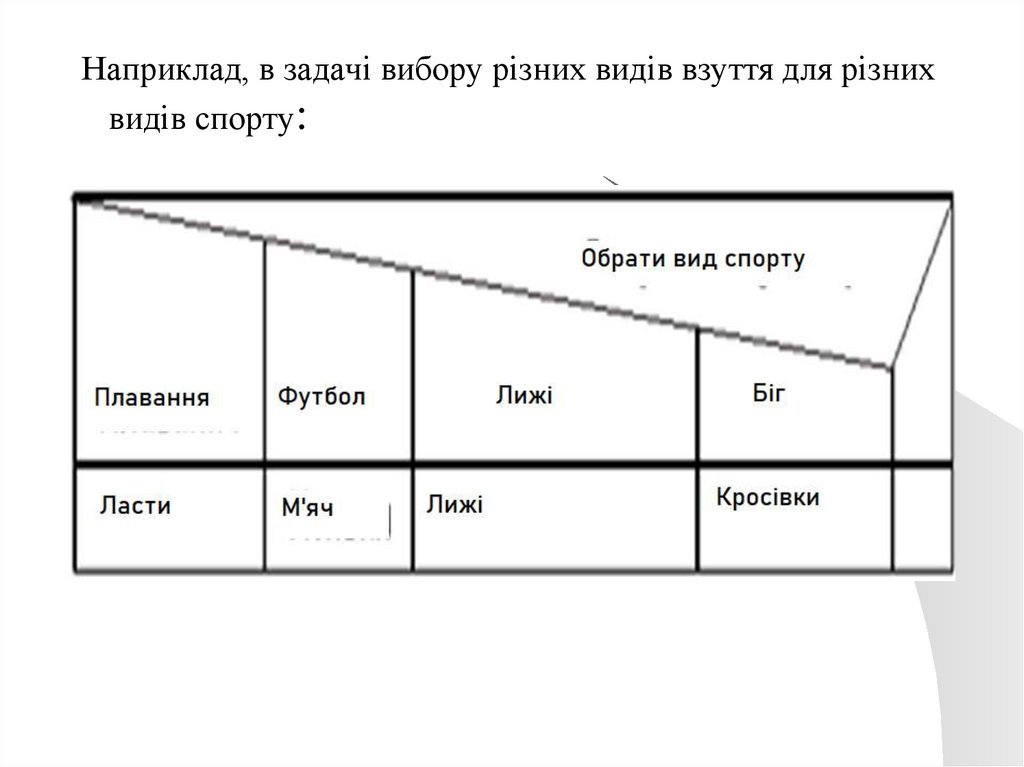
Блок множинного виборуБлок множинного вибору використовується, коли існує
кілька варіантів можливих дій, вибір яких залежить від
значення деякого виразу
62.
Наприклад, в задачі вибору різних видів взуття для різнихвидів спорту:
63.
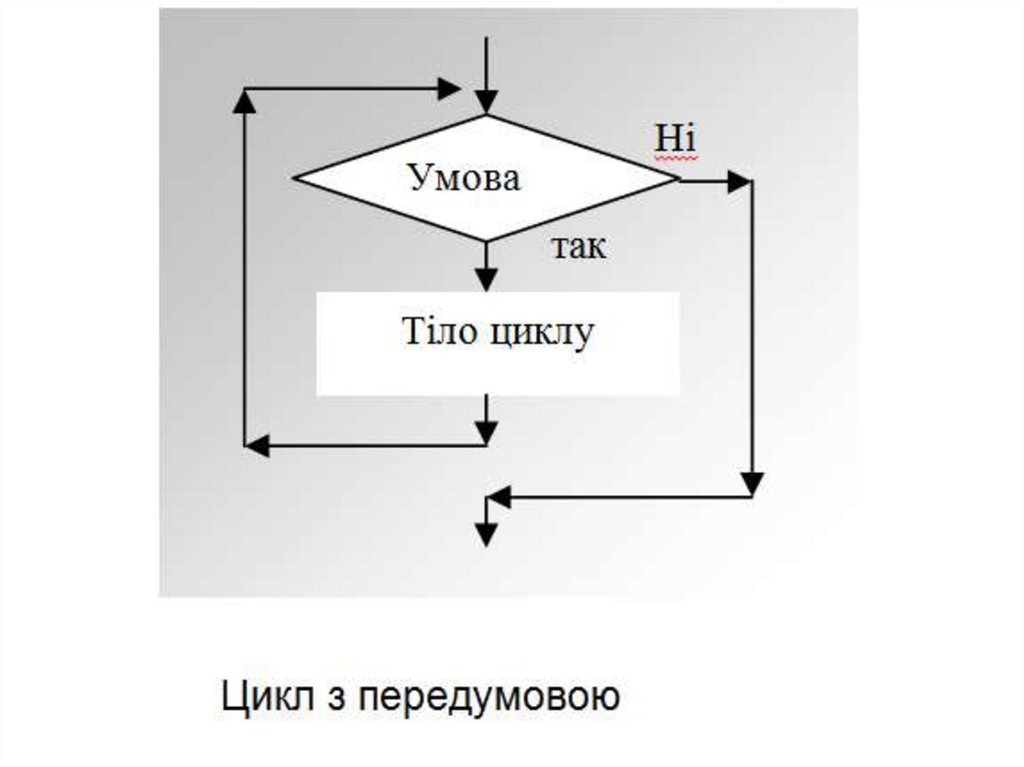
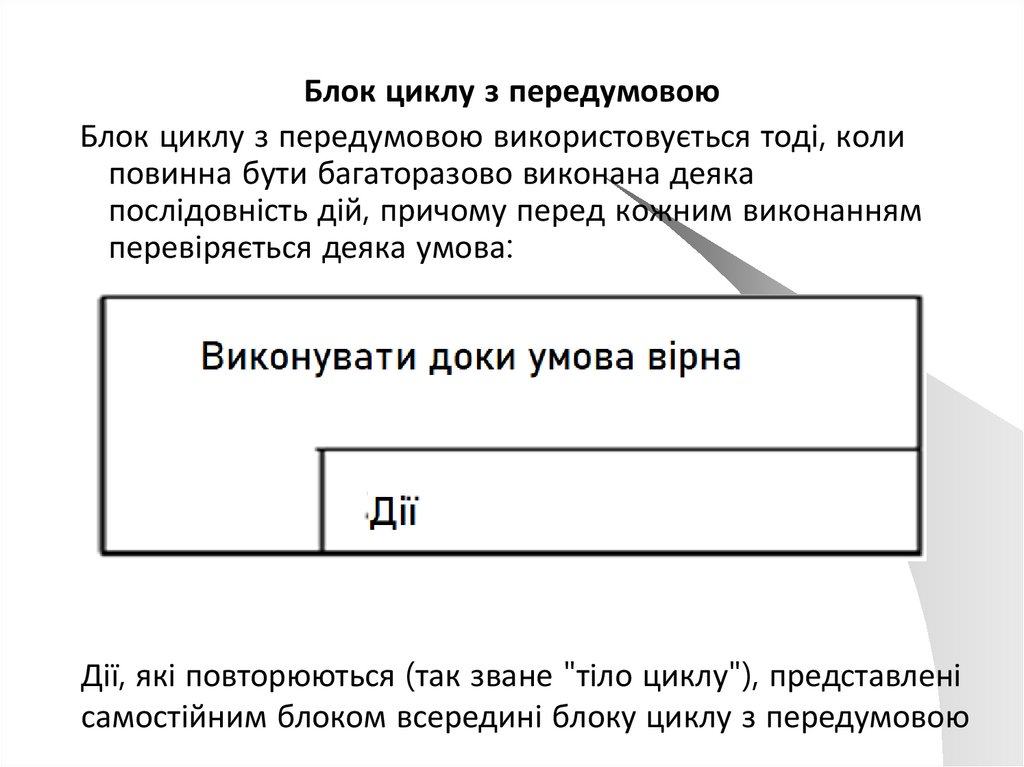
Блок циклу з передумовоюБлок циклу з передумовою використовується тоді, коли
повинна бути багаторазово виконана деяка
послідовність дій, причому перед кожним виконанням
перевіряється деяка умова:
Дії, які повторюються (так зване "тіло циклу"), представлені
самостійним блоком всередині блоку циклу з передумовою
64.
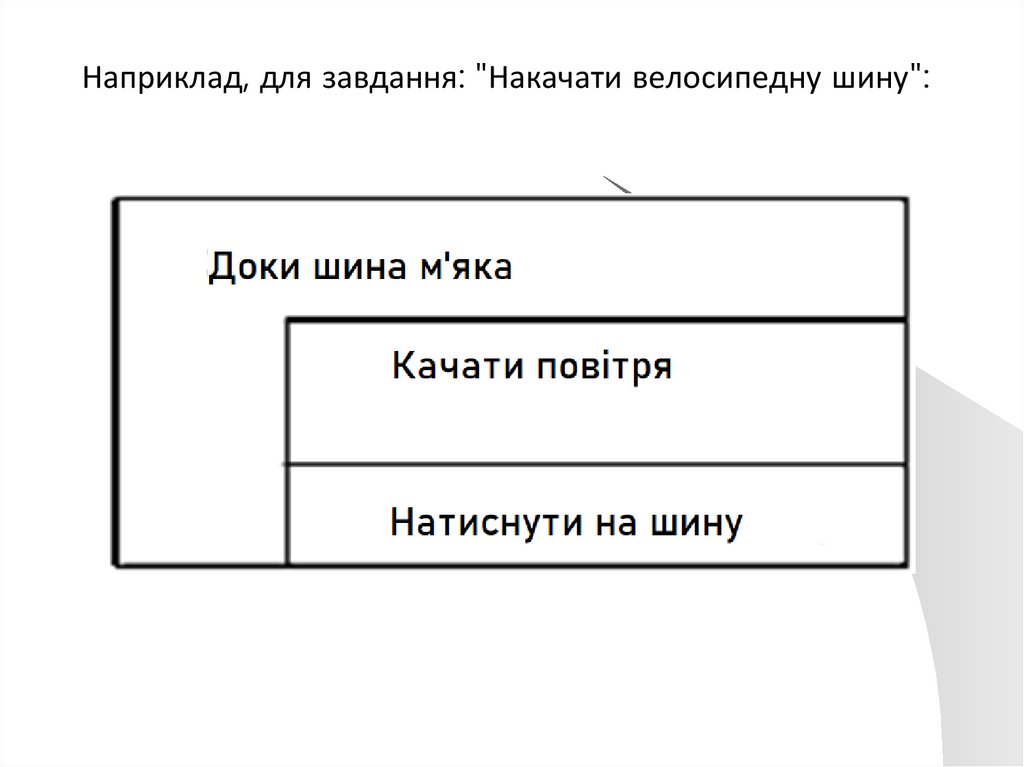
Наприклад, для завдання: "Накачати велосипедну шину":65.
Блок циклу з постумовоюБлок циклу з постумовою використовується, коли в
алгоритмі дії повинні повторюватися до настання певної
умови (умова перевіряється після виконання дій). Дії в
циклі з постумовою завжди виконуються хоча б один
раз, тому що перевірка здійснюється в кінці циклу.
66.
Наприклад, в завданні приготування тіста для млинців:67.
68.
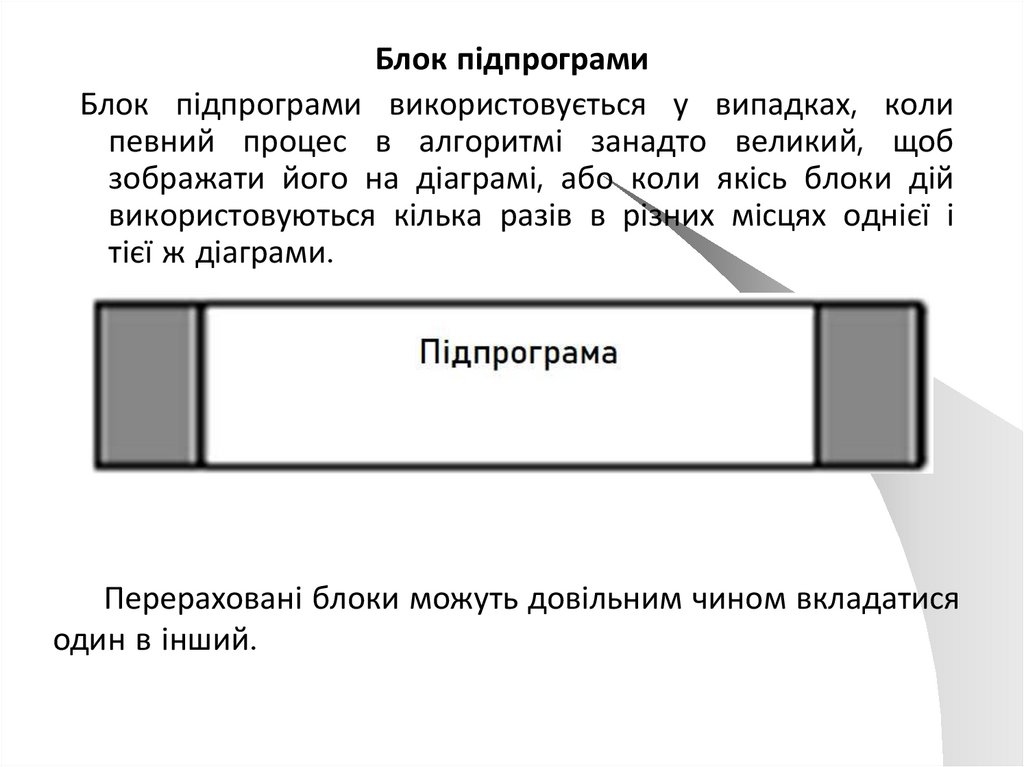
Блок підпрограмиБлок підпрограми використовується у випадках, коли
певний процес в алгоритмі занадто великий, щоб
зображати його на діаграмі, або коли якісь блоки дій
використовуються кілька разів в різних місцях однієї і
тієї ж діаграми.
Перераховані блоки можуть довільним чином вкладатися
один в інший.
69.
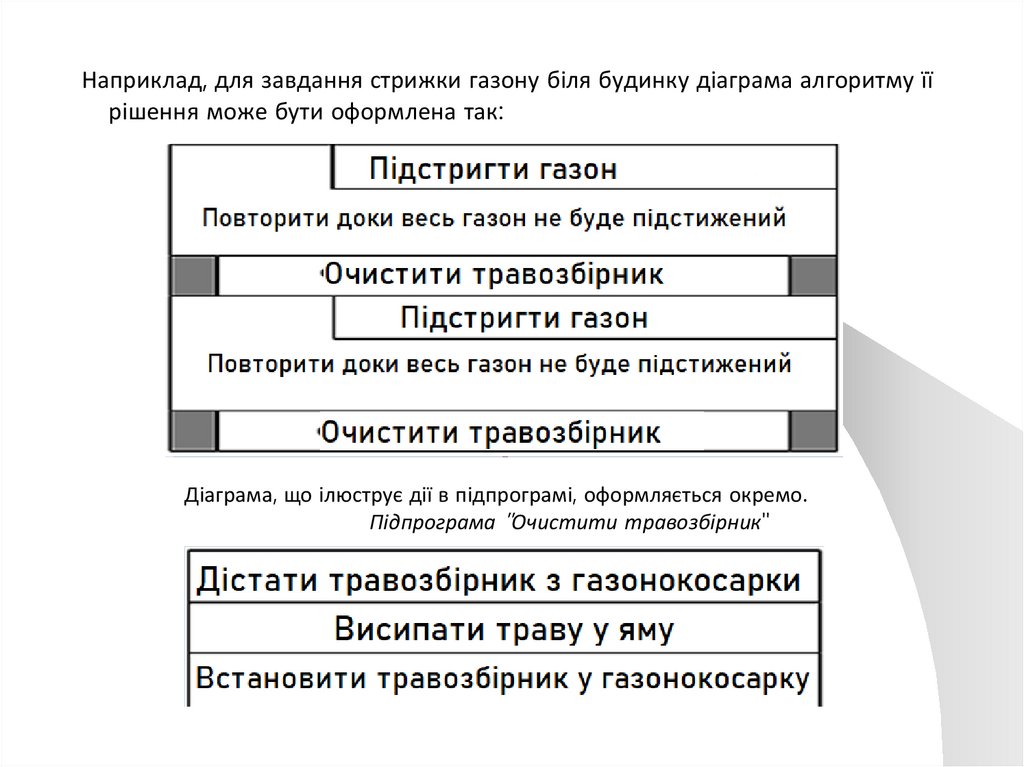
Наприклад, для завдання стрижки газону біля будинку діаграма алгоритму їїрішення може бути оформлена так:
Діаграма, що ілюструє дії в підпрограмі, оформляється окремо.
Підпрограма "Очистити травозбірник"
70.
Алгоритмічні мови- це спеціальний засіб,призначений для запису алгоритмів в
аналітичному вигляді. Алгоритмічні мови
близькі до математичних виразів і до
природних мов. Кожен алгоритмічний
мову має свій словник. Алгоритм,
записаний
на
алгоритмічній
мові,
виконується за суворими правилами
цього конкретного мови.
71.
Операційні схеми алгоритмів.Суть цього способу опису алгоритму полягає в
тому, що кожен оператор позначається буквою
(наприклад, А - арифметичний оператор, Р логічний оператор і т.д.).
Оператори
записуються
зліва направо
в
послідовності їх виконання, причому, кожен
оператор має індекс, який вказує порядковий
номер оператора. Алгоритм записується в один
рядок у вигляді послідовності операторів.
72.
Псевдокодсистемакоманд
абстрактної машини. Цей спосіб
запису алгоритму за допомогою
операторів
близьких
до
алгоритмічних мов.
73.
Що характеризуєбудь-який
алгоритм?
Складність
74.
Вміння проводити аналіз обчислювальноїскладності алгоритму є одним з основних
вмінь в професійній діяльності ІТ-фахівця
75.
Навіщо проводити аналіз алгоритму ?Причини для аналізу алгоритму:
практичні
– необхідність отримання оцінок або границь для
обсягу пам’яті або часу роботи;
теоретичні
– необхідність порівняння алгоритмів (за певним
критерієм);
– необхідність виявлення найбільш ефективних
алгоритмів (за набором критеріїв);
– необхідність оцінки доцільності подальшого
покращення алгоритму.
76.
Як проводити аналіз алгоритму?При аналізі поводження функції трудомісткості
алгоритму часто використовують прийняті в
математиці асимптотичні позначення, що
дозволяють показати швидкість росту функції,
маскуючи при цьому конкретні коефіцієнти.
Така оцінка функції трудомісткості алгоритму
називається складністю алгоритму й дозволяє
визначити переваги у використанні того або
іншого алгоритму для більших значень
розмірності вихідних даних.
77.
Нехай А – алгоритм для розв’язку певного класузадач, а n – розмірність окремої задачі цього класу. В
багатьох задачах теорії графів, наприклад, n – кількість
вершин графа. В загальному випадку n може бути
кількістю
елементів
масиву
або
довжиною
послідовності, що вводиться.
Визначимо fA(n) як робочу функцію, що дає
верхню границю для максимального числа основних
операцій (додавання, порівняння і т.д.), які повинен
виконати алгоритм А для розвозку будь-якої задачі
розмірності n.
78.
Наступне позначення стандартне в багатьох математичнихдисциплінах, в тому числі в аналізі алгоритмів.
Функцію f(n) визначають як O(g(n)) і говорять, що вона порядку
g(n) для великих n, якщо
f ( n)
const 0
lim
n g ( n)
Функція h(n) є o[z(n)] для великих n, якщо
h( n)
0
lim
n z ( n)
Ці символи читаються, відповідно, як «O велике від n» та «o
мале від n». Інтуїтивно, якщо f(n) є O(g(n)), то ці дві функції
зростають з однаковою швидкістю при n→∞. Якщо f(n) є
о(g(n)), то g(n) зростає набагато швидше, ніж f(n).
79.
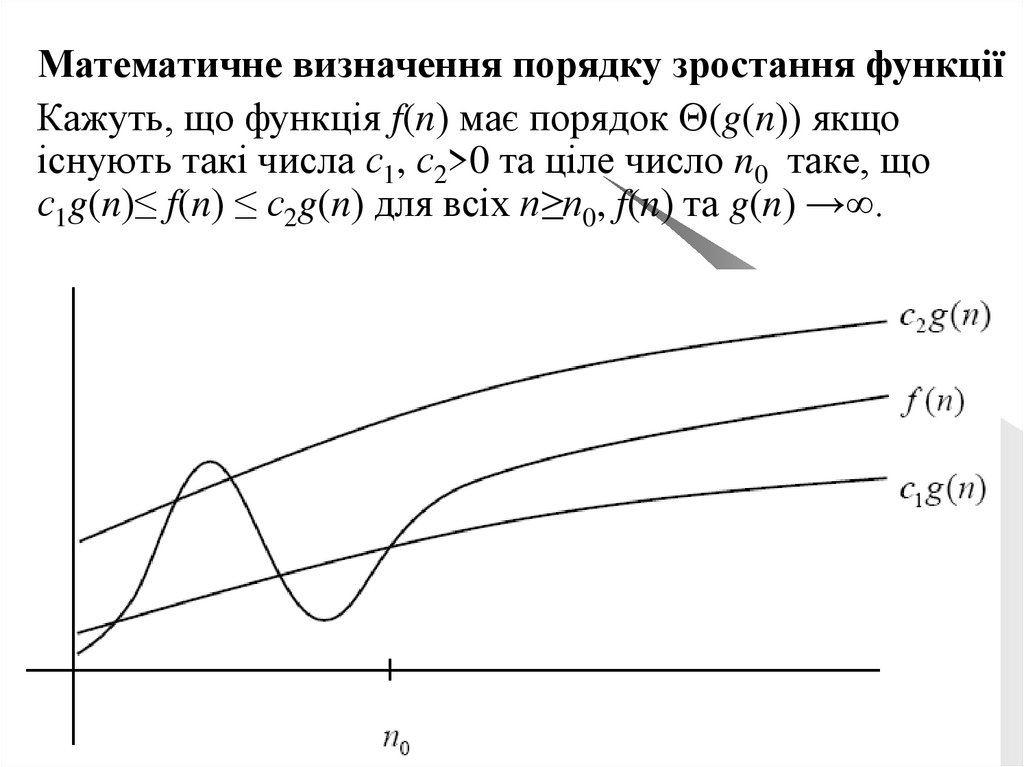
Математичне визначення порядку зростання функціїКажуть, що функція f(n) має порядок (g(n)) якщо
існують такі числа с1, с2>0 та ціле число n0 таке, що
с1g(n)≤ f(n) ≤ с2g(n) для всіх n≥n0, f(n) та g(n) →∞.
80.
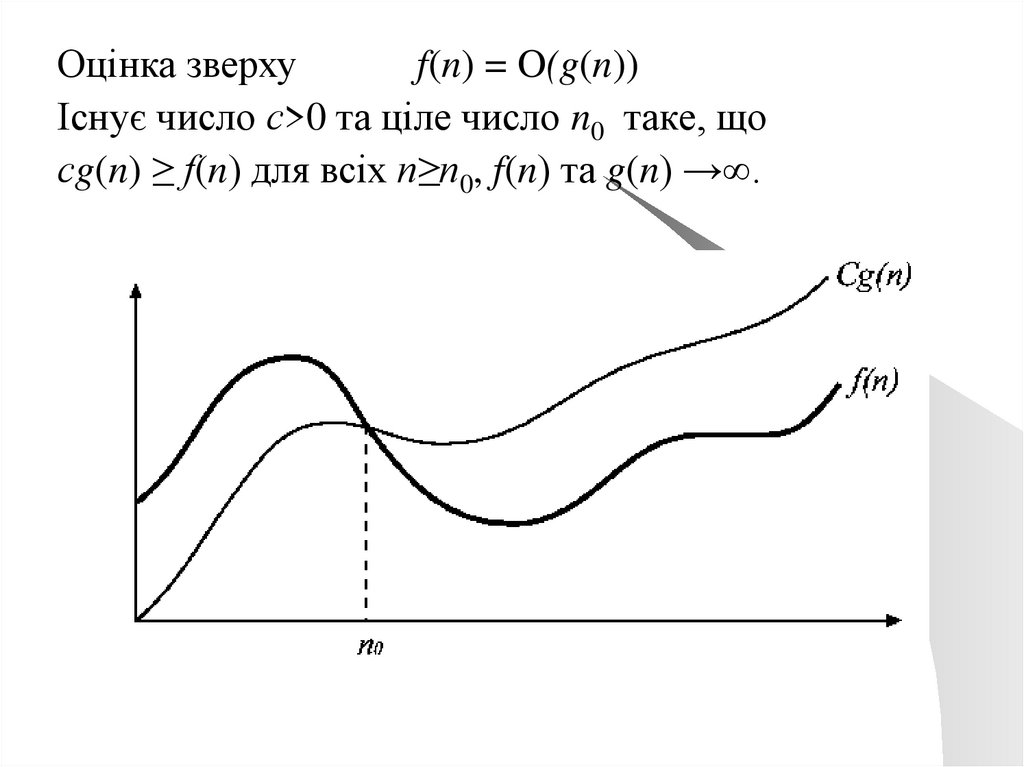
Оцінка зверхуf(n) = O(g(n))
Існує число с>0 та ціле число n0 таке, що
сg(n) ≥ f(n) для всіх n≥n0, f(n) та g(n) →∞.
81.
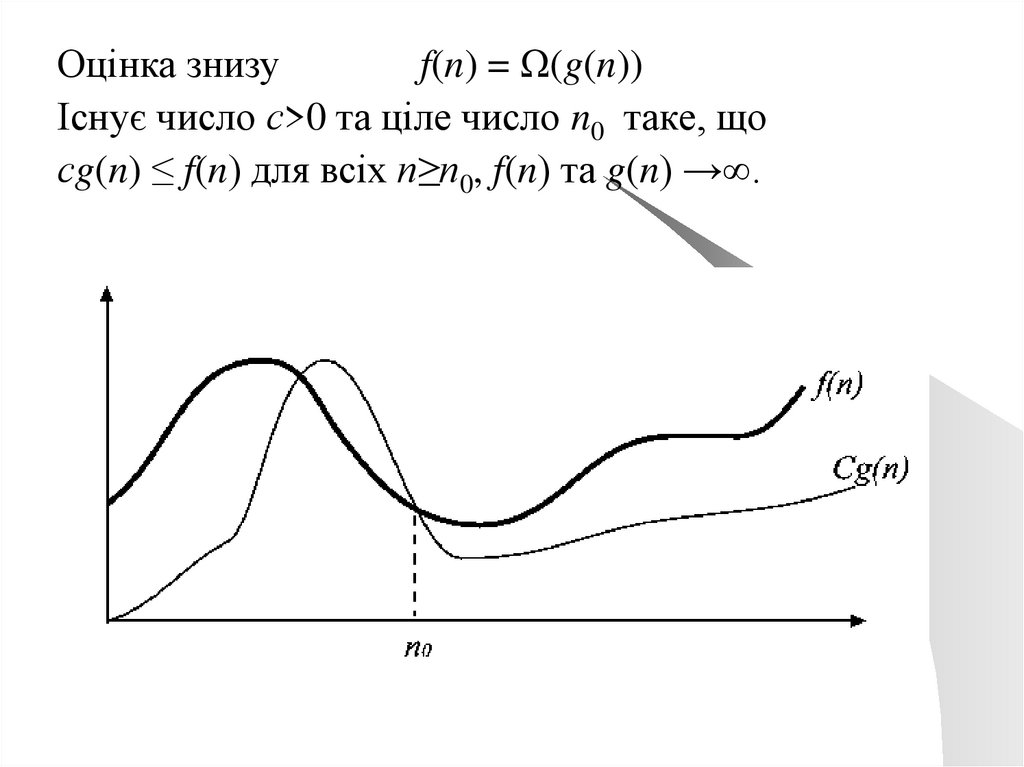
Оцінка знизуf(n) = Ω(g(n))
Існує число с>0 та ціле число n0 таке, що
сg(n) ≤ f(n) для всіх n≥n0, f(n) та g(n) →∞.
82.
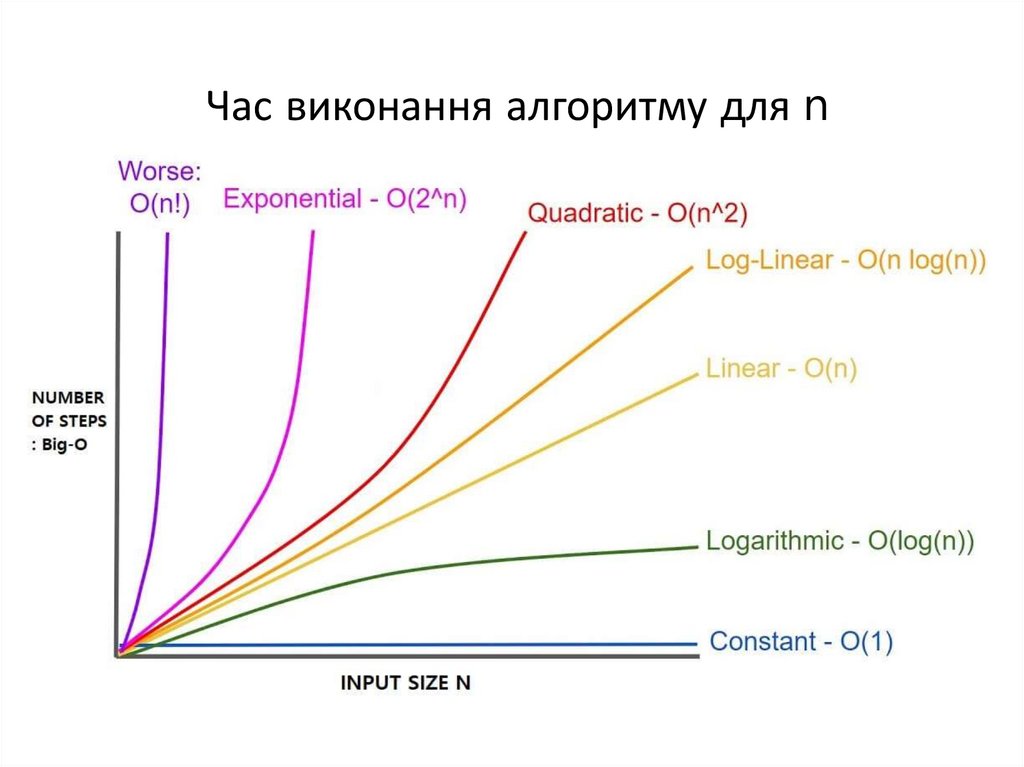
Класи складності алгоритмівКонстантні алгоритми f(n) = O(1) – час їх виконання
обмежено константою, яка не залежить від розміру
вхідних даних;
Логарифмічні алгоритми f(n) = O(log n) – основу
логарифму можна не враховувати, оскільки перехід до
іншої основи є множенням на константу;
Лінійні алгоритми f(n) = O(n);
Квадратичні алгоритми f(n) = O(n2);
Поліноміальні алгоритми f(n) = O(nk);
Експоненційні алгоритми f(n) = O(an); відмітьте, що n!=
Ω(2n) і n! = O(nn).
83.
Час виконання алгоритму для n84.
Розглянемо, як виконуються операції додавання імноження з використанням О-символіки.
Правило сум. Нехай T1(n) і Т2(n) - час виконання двох
програмних фрагментів Р1 і Р2 , T1(n) має ступінь
зростання O(f(n)), а Т2(n) - O(g(n)). Тоді T1(n)+Т2(n),
тобто час послідовного виконання фрагментів Р1 і Р2,
має ступінь зростання O(max(f(n), g(n))).
Для доказу цього пригадаємо, що існують константи с1, с2,
n1 і n2 такі, що при n≥n1 виконується нерівність T1(n)≤с1f(n), і,
аналогічно, Т2(n)≤с2g(n), якщо n≥n2. Хай n0=max(n1, n2). Якщо
n≥n0, то, очевидно, що T1(n)+Т2(n)≤с1f(n)+с2g(n). Звідси витікає,
що при n≥n0 справедлива нерівність
T1(n)+Т2(n)≤(с1+с2)max(f(n),g(n)). Остання нерівність і означає,
що T1(n)+Т2(n) має порядок зростання O(max(f(n),g(n))).
85.
Приклад. Правило сум використовується дляобчислення часу послідовного виконання програмних
фрагментів з циклами і галуженнями.
Хай є три фрагменти з часом виконання відповідно O(n3), O(n2)
і О(n log n). Тоді час послідовного виконання перших двох
фрагментів має порядок O(max(n2, n3)), тобто О(n3). Час
виконання всіх трьох фрагментів має порядок
O(max(n3, n log n)), це те ж саме, що О(n3).
У загальному випадку час виконання кінцевої
послідовності програмних фрагментів, без урахування
констант, має порядок фрагмента з найбільшим часом
виконання.
З правила сум також виходить, що якщо g(n)≤f(n) для
всіх n, що перевищують n0, то вираз O(f(n)+ g(n))
еквівалентний O(f(n)). Наприклад, О(n2+n) те ж саме,
що О(n2).
86.
Правило добутків. Якщо T1(n) і Т2(n) мають степенізростання O(f(n)) і O(g(n)) відповідно, то добуток
T1(n)Т2(n) має ступінь зростання O(f(n) g(n)).
З правила добутків витікає, що O(cf(n)) еквівалентно
O(f(n)), якщо с - додатна константа. Наприклад,
О(n2/2) еквівалентно О(n2).
87.
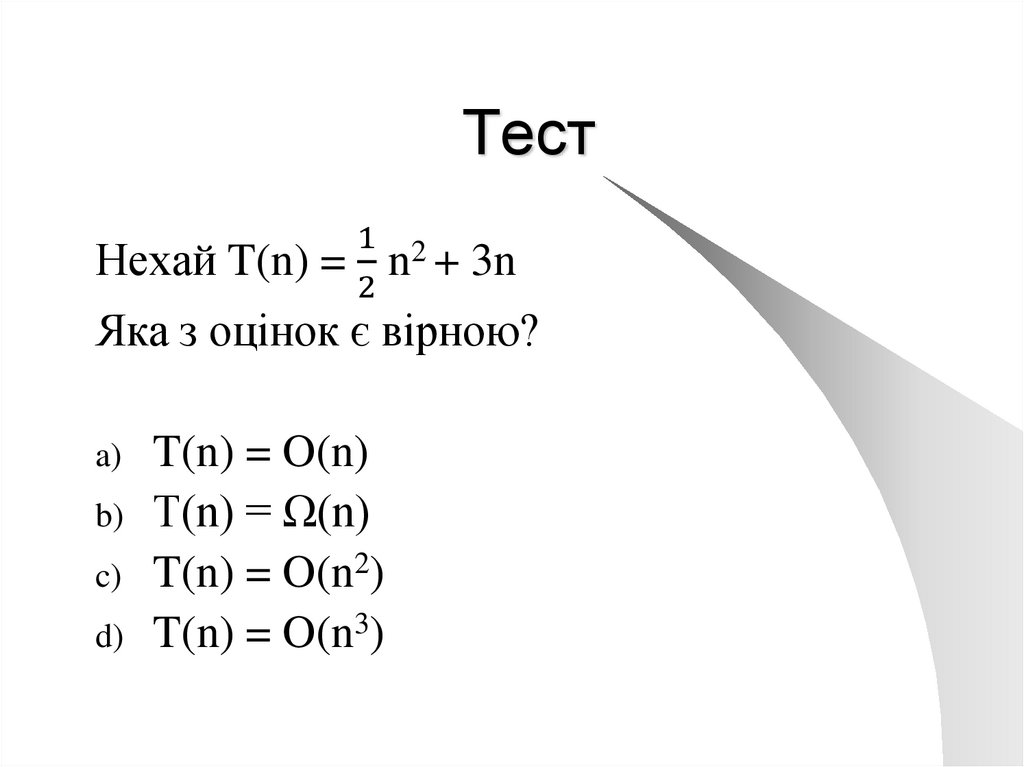
Тест1 2
Нехай T(n) = n + 3n
2
Яка з оцінок є вірною?
T(n) = O(n)
b) T(n) = Ω(n)
c) T(n) = O(n2)
d) T(n) = O(n3)
a)
88.
Загальні правила обчислення часу виконання програми1. Час виконання операторів присвоєння, читання і
запису зазвичай має порядок О(1). Є декілька
виключень з цього правила, де можна присвоювати
великі масиви, або в будь-яких інших мовах, що
допускають виклики функцій в операторах
присвоєння.
2. Час виконання послідовності операторів визначається
за допомогою правила сум. Тому ступінь зростання
часу виконання послідовності операторів без
визначення констант пропорційності співпадає з
найбільшим часом виконання оператора в даній
послідовності.
89.
3. Час виконання умовних операторів складається з часувиконання умовно виконуваних операторів і часу
обчислення самого логічного виразу. Час обчислення
логічного виразу зазвичай має порядок О(1). Час для
всієї конструкції if-then-else складається з часу
обчислення логічного виразу і найбільшого часу,
необхідного для виконання операторів, виконуваних
при значенні логічного виразу true і при значенні
false.
90.
4. Час виконання циклу є сумою часу всіх виконуванихітерацій циклу, операторів тіла циклу, що у свою чергу
складаються з часу виконання і часу обчислення
умови припинення циклу (зазвичай останнє має
порядок О(1)). Часто час виконання циклу
обчислюється, нехтуючи визначенням констант
пропорційності, як добуток кількості виконаних
ітерацій циклу на найбільший можливий час
виконання операторів тіла циклу. Час виконання
кожного циклу, якщо в програмі їх декілька, повинен
визначатися окремо.
91.
5. Для програм, що містять декілька процедур (середяких немає рекурсивних), можна підрахувати
загальний час виконання
програми
шляхом
послідовного знаходження часу виконання процедур,
починаючи з тієї, яка не має викликів інших процедур.
Якщо є рекурсивні процедури, потрібно з кожною
рекурсивною процедурою зв'язати часову функцію
Т(n), де n визначає обсяг аргументів процедури; потім
отримати рекурентне співвідношення для Т(n), тобто
рівняння (або нерівність) для Т(n), де беруть участь
значення T(k) для різних значень k.
92.
Прикладint max = a [0];
for (int i = 1; i
<n; i ++)
if (max <a [i])
max = a [i];
t1 - присвоювання
t2 - ітерація
t3 - порівняння
t4 - присвоювання
f (n) = t1 + (t2 + t3 + t4) * (n-1) <(t1 + t2
+ t3 + t4) * (n-1) <<C * (n-1) <C * n = C * g
(n), де g (n) = n
Таким чином f (n) ~ O (n) лінійна
складність
93.
Визначити складність наступнихалгоритмів:
1. Додавання двох чисел
1. Додавання мільйона чисел
2. Додавання елементів масиву з n
елементів
3. Додавання елементів двовимірного
масиву, що складається з n рядків і n
стовпців
4. Алгоритм піднесення числа x до
натурального ступеня n
94.
Деякі математичніспіввідношення
95.
Визначити складність алгоритмуfor (int i = 0; i < n; ++i) { // B
for (int j = 1; j < m; ++j) { // A
a[i][j]++; // С
}
}
96.
Визначити складність алгоритмуfor (int i = 0; i < n-1; ++i) { // B
for (int j = 0; j < n-i; ++j) { // A
a[i][j]++;
}
}
97.
Визначити складність алгоритмуfor (int i = 0; i < n; ++i) { // B
for (int j = i; j < n-i; ++j) { // A
a[i][j]++;
}
}
98.
Визначити складність алгоритмуfor (int i = 0; i < n; ++i) { // B
for (int j = 1; j < n; j *= 2) { // A
a[i][j]++;
}
}
99.
Визначити складність алгоритмуfor (int i = 0; i < 100; ++i) { // B
for (int j = 1; j < n; ++j) { // A
++count;
}
}
100.
Визначити складність алгоритмуfor (int i = 0; i < n; ++i) { // B
for (int j = 0; j < n / i; ++j) { // A
matrx[i][i]++;
}
}
101.
На час виконання програми впливають наступнічинники:
– Введення початкової інформації в програму
(зокрема, її розмір).
– Якість скомпільованого коду програми.
– Машинні інструкції (природні і прискорюючі),
використані для виконання програми.
– Складність
алгоритму
відповідної
програми
(кількість кроків алгоритму).
102.
Важливо також знати, наскільки погано працюєекспоненційний алгоритм. Існує багато важливих
задач, для яких на даний момент відомі лише
експоненційні алгоритми. Ці задачі мусимо
розв’язувати, бо вони мають велику практичну
значимість. Якщо відомі лише експоненційні
алгоритми, то хотілось би користуватися найбільш
ефективними з них. Очевидно, що слід віддати
перевагу алгоритму, що розв’язує задачу розмірності n
за О(2n) кроків, перед алгоритмами, що розв’язують її
за О(n!) або О(nn) кроків.
103.
Необхідно підкреслити, що ступінь зростанняякнайгіршого часу виконання - не єдиний або
найважливіший критерій оцінки алгоритмів і програм.
1. Якщо створювана програма буде використана тільки
кілька разів, тоді вартість написання і наладки
програми домінуватиме в загальній вартості програми,
тобто фактичний час виконання не дасть істотного
впливу на загальну вартість. В цьому випадку слід
віддати перевагу алгоритму, найбільш простому для
реалізації.
104.
2. Якщо програма працюватиме тільки з "малими"вхідними даними, то степінь зростання часу
виконання матиме менше значення, ніж константа,
присутня у формулі часу виконання.
Разом з тим і поняття "менших" вхідних даних
залежить від точного часу виконання конкуруючих
алгоритмів. Існують алгоритми, такі як алгоритм
цілочисельного
множення,
асимптотично
найефективніші, але які ніколи не використовують на
практиці навіть для великих завдань, оскільки їх
константи пропорційності значно перевершують
подібні константи інших, більш простих і менш
"ефективних" алгоритмів.
105.
3. Ефективні, але складні алгоритми можуть бутинебажаними, якщо готові програми підтримуватимуть
особи, що не беруть участь в написанні цих програм.
4. Відомо декілька прикладів, коли ефективні алгоритми
вимагають таких великих об'ємів машинної пам'яті
(без можливості використання повільніших зовнішніх
засобів зберігання), що цей чинник зводить нанівець
перевагу "ефективності" алгоритму.
5. У чисельних алгоритмах точність і стійкість алгоритмів
не менш важливі чим їх часова ефективність.
106.
Коли варто проводити аналіз алгоритму?Доцільно підкреслити, що до етапів повної побудови алгоритму не
треба відноситись як до чогось незмінного. Деякі етапи можуть
виконуватись одночасно з іншими, деякі можуть навіть бути пропущеними.
Якщо є хороша модель, то, мабуть, не має потреби будувати іншу.
Звичайно, неможливо довести правильність алгоритму до того, як він буде
розроблений, але, можливо, краще провести деякий аналіз процесу
розробки алгоритму до того, як почати його реалізовувати. Це тим більш
так, якщо є привід припускати, що алгоритм буде експоненційним.
Деякий аналіз на стадії розробки може підказати, як зробити
алгоритм більш ефективним. І, нарешті, етапи процесу побудови можуть
буди з вигодою переглянуті після того, як вони вже вважаються
завершеними. Наприклад, фази аналізу та перевірки можуть забезпечити
цінний зворотній зв'язок з етапами розробки та реалізації.
107.
Перевірка програмиІснує три аспекти перевірки програми:
На правильність
На ефективність реалізації
На обчислювальну складність
Разом узяті ці перевірки спрямовані на отримання
експериментальної відповіді на питання: чи працює
алгоритм? Наскільки добре він працює?
108.
Перевірка правильностіпідтверджує, що програма робить саме те, для
чого вона була призначена. Важливо зрозуміти, що
математична бездоганність алгоритму не гарантує
правильності перекладу його в програму. Аналогічно
ні відсутність діагностичних повідомлень компілятора,
ні «розумний вигляд» результатів прогону не дають
достатньої гарантії правильності програми. Це часто
ілюструють приклади багатьох програм, які працюють
місяці або навіть роки до того як в них виявляються
помилки.
Далі перераховано, на що варто звернути увагу
при перевірці правильності програми.
109.
Міри безпеки.Легше перевіряти правильність програми, якщо
більш ранні кроки її побудови були ретельно
організовані та виконані. В значній мірі розвиток
структурного
програмування
згори-вниз
був
мотивований цими міркуваннями.
Плануйте перевірку програми в процесі її
розробки, думайте про те, як можна перевірити
кожен модуль і які слід використати для цього дані,
ще в процесі його написання.
Плануйте наперед зміни, які передбачаються в
програмі в майбутньому. Задайтеся запитанням, які
саме зміни найімовірніше доведеться зробити?
Здорова турбота про універсальність програми
допоможе уникнути витратних переробок цілих
сегментів написаної програми.
110.
Локальні перевірки.Ряд простих тестів, або перевірок може бути виконаний
вручну.
Перевіряйте відповідність між оператором алгоритму
або блок-схеми і його реалізацією в програмі.
Виконайте локальні перевірки описів усіх змінних,
міняючи всі входження змінної, ім’я якої було змінене.
Перевірте відповідність розмірностей масивів.
Встановіть оператори наладки або друку. Виконуйте
всі зміни відразу ж, як тільки в них виникла
необхідність, або принаймні відмічайте їх, інакше їх
легко забути.
111.
Перевірка на неприпустимі значення. В кожномуоператорі, якщо це можливо, розгляньте можливість
появи неприпустимого значення деякої змінної і
спробуйте визначити причину, з якої це могло б
трапитися. Переконайтеся, що всі змінні ініціалізовані
правильно, наприклад, при кожному виклику
підпрограми. Переконайтеся, що індекси не можуть
приймати занадто малі або занадто великі значення.
Крім того перевірте, щоб неприпустимі значення не
могли бути внесені зовні в підпрограму.
Перевірка на нескінчені цикли. Спробуйте визначити, чи
існує шлях, по якому програма могла б потрапити в
нескінчений цикл.
112.
Перевірка усіх частин програми.Перевіряйте доти, доки кожен присутній в програмі
оператор не буде давати правильний результат.
Зокрема, перевірте кожну гілку і кожну умову
помилки хоча б один раз. Намагайтеся перевірити
якомога більше різних шляхів через програму.
Зверніть увагу на те, що програми із структурою
дерева мають набагато менше шляхів, ніж програми із
складними структурами циклів.
113.
Тестові дані.Значні зусилля слід направити на отримання хороших
даних для перших же тестів. Початковий набір
тестових даних повинен покривати широкий діапазон
часткових випадків; обов’язково повинні бути відомі
вірні відповіді. Потрібно включати дані, що
перевіряють усі умови помилок. Можна також
пропустити через програму які-небудь беззмістовні
дані, щоб подивитися, чи вірно вони оброблюються.
Уникайте прогону даних, які по суті вимагають, щоб
система знову і знову виконувала те ж саме. Також
намагайтеся уникати тестових даних, відповіді на які
не можна перевірити. Випадкові дані зазвичай мають
обидва ці недоліки.
114.
Перевіряйте програму на даних, що лежать на границяхдопустимих діапазонів. Якщо діапазон для вхідних
даних визначається розміром задачі, зробіть окрему
спробу перевірити дуже великі і дуже маленькі задачі.
Зверніть особливу увагу на нульові випадки. Наприклад,
порожні рядки, графи без вершин або ребер, нульові
матриці, тощо. Якщо програмою будуть користуватися
часто, то можете бути впевнені, що усі можливі крайні
випадки рано чи пізно проявляться. Перевірте їх
вчасно.
115.
Перевіряйте програму на даних, що виходять за межіприпустимого діапазону вхідних даних. Остерігайтеся
небезпечної ситуації, коли програма видає
правдоподібні, але невірні результати. Якщо доступна
інша програма, що розв’язує цю ж задачу,
використайте її для контролю програми, що
перевіряється. Хоча це і мало імовірно, майте на увазі,
що обидві програми можуть виявитися
неправильними.
Слід також витратити деякі зусилля, щоб перевірити
програму на реальних даних, якщо передбачається її
практичне використання. Може виявитися необхідною
співпраця з потенційними користувачами.
116.
Пошук скритих помилок.Випробуйте все, що зможете придумати, щоб виявити в
програмі помилку. Якщо можливо, попросіть когонебудь іншого зробити це. Свіжий погляд може бути
саме тим, що потрібно для локалізації непоміченої
вами помилки.
Час, що необхідний для перевірки.
Перевірка вимагає зазвичай суттєвої кількості часу, і не
слід її пришвидшувати. Зарезервуйте для наладки
досить часу.
117.
Повторна перевірка.Якщо під час перевірки виявлено помилки, потрібно
зробити зміни, щоб їх виправити. Слід потурбуватися
про те, щоб не нагромаджувати одне виправлення на
інше. Потрібно встановити всі місця програми, на які
впливає
дана
помилка.
Переконайтеся,
що
виправлення однієї помилки не породжує нових. З
цією метою можна було б зберегти старі тестові дані і
використати їх для повторної перевірки програми.
Коли припинити перевірку?
Для будь-якої конкретної програми відповідь залежить
від її можливого застосування та від рівня
впевненості, якого бажає досягти програміст. Часто
питання вирішується виходячи з наявних часу та
коштів.
118.
Перевірка ефективності реалізаціїнаправлена на відшукання способів змусити правильну
програму працювати швидше або витрачати менше пам’яті.
Щоб покращити програму, переглядаються результати етапу
реалізації в процесі побудови алгоритму.
Така перевірка виявляється втратою часу для простих
програм, або для програм, якими будуть користуватися рідко,
але дуже корисна для програм, якими будуть користуватися
часто.
Доцільно застерегти, що гранично ефективне кодування
може порушити ясність програми і зробити перевірку її
правильності набагато важчою. Взагалі слід уникати змін, що
загрожують зрозумілості, якщо вони не можуть бути
виправдані суттєвою економією часу або пам’яті.
119.
Методи підвищення ефективності програмимашинно незалежні:
Арифметичні операції.
Арифметичні операції додавання та віднімання
виконуються швидше ніж множення та ділення.
Зведення в степінь – найповільніша операція. Крім
того, цілочисельна арифметика за звичай швидше
арифметики дійсних чисел. Таким чином величину X2
швидше обрахувати як X*X, а X+X може виявитися
швидше ніж 2.0*X.
Надлишкові обчислення.
Якщо складний вираз зустрічається більше ніж в одному
місці обчислюйте його один раз та надавайте
обчислене значення змінній.
120.
Порядок в логічних виразах.Більшість компіляторів припиняють обчислення логічних
виразів як тільки результат отримано. Наприклад в
виразі (A or B or C), обчислення буде припинено, як
тільки буде знайдено значення TRUE. Певний час
можна зекономити, розмістивши A, B, C так, щоб A
найімовірніше виявилося істинним, B - наступним по
величині ймовірності, а C - з найменшою імовірністю.
Виключення, розгортання та спрощення циклів.
Найбільші можливості підвищення ефективності
виконання криються в сегментах програми, що часто
повторюються. Такі сегменти майже завжди мають
форму циклів. Одним з методів скорочення витрат
часу на цикли є скорочення кількості повторів.
121.
Профілі виконання.Один із хороших способів знаходження фрагменту програми, що
є найбільш ресурсоємним, складається в побудові профілю
виконання програми. Робота програми контролюється набором
таймерів та лічильників і видається лістинг, який показує,
скільки разів виконався кожний оператор і скільки одиниць
часу витрачено на виконання кожного оператора.
Зазвичай в засобах наладки є бібліотечні програми, що
допомагають згенерувати такі профілі. Якщо ж немає готового
пакета програм для побудови профілю, неважко зібрати грубі
профілі.
Статистичні дослідження з використанням профілів виконання
виявили примітний факт, що приблизно 5% обсягу більшості
програм потребують приблизно 50% часу виконання.
122.
Профілі виконання корисні не тільки для перевіркиефективності реалізації, але і для інших двох типів
перевірки.
При перевірці правильності ці профілі можна
використовувати для того, щоб побачити які сегменти
програми виконуються, а які ні. Таким чином, профілі
можуть допомогти перевірити, чи всі частини
програми протестовані.
Профілі
також
корисні
для
проведення
експериментального детального аналізу складності на
основі послідовного перегляду операторів.
123.
Перевірка обчислювальної складності зводиться доекспериментального аналізу складності алгоритму або
до експериментального порівняння двох чи більше
алгоритмів, що розв’язують одну і ту ж саму задачу.
Крім того, перевірки цього типу застосовуються для
доповнення теоретичного аналізу алгоритму. Якщо
теоретичний аналіз занадто важко провести,
необхідно все ж накопичити певний обчислювальний
досвід роботи з цим алгоритмом. Цей досвід можна
використовувати наприклад, для передбачення
тривалості роботи програми на певному наборі
вхідних даних. Результати
експериментального
аналізу рідко виявляються вичерпними, тому не слід
виходити за розумні межі при їх інтерпретації.
























































































 database
database








