Similar presentations:
Движение в математике через основные понятия симметрии
1.
Движение в математикечерез основные понятия
симметрии
2.
раскрыть математический смысл понятия движенияв математике
через
центральную симметрию
осевую симметрию
параллельный перенос
зеркальное отображение
и сравнить с движением в астрономии, физике,
химии и т.д.
3.
1) Определение движения в школьном курсе математики напримере центрального, осевого, зеркального отображения,
параллельного переноса, поворота.
2) Метопредметность движения в математике связана с
космическим пространством.
3) Время и его земные мерки.
4) Голографическое измерение пространства через движения
в математике.
4.
5.
6.
Математика строгая наука.Понятие время существует только на
Земле и связанно с жизнью
«живого».
Как же математика представляет
движение?
7.
8.
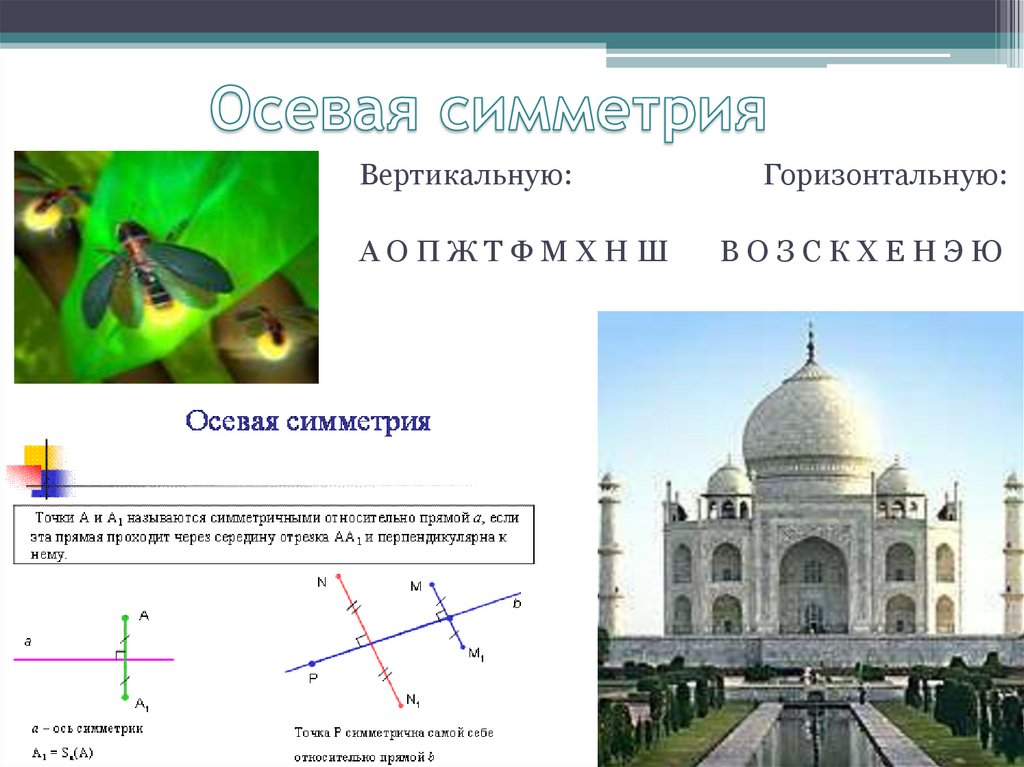
Вертикальную:АОПЖТФМХНШ
Горизонтальную:
ВОЗСКХЕНЭЮ
9.
Отражение, зеркальное отражение или зеркальнаясимметрия — движение евклидова пространства,
множество неподвижных точек которого является
гиперплоскостью (в случае трехмерного пространства —
просто плоскостью).
Термин зеркальная симметрия употребляется также для
описания соответствующего типа симметрии объекта, то
есть, когда объект при операции отражения переходит в
себя.
Это математическое понятие описывает соотношение в
оптике объектов и их (мнимых) изображений при
отражении в плоском зеркале, а также многие законы
симметрии (в кристаллографии, химии, физике, биологии
и т. д., а также в искусстве и искусствоведении)
10.
Параллельный перенос все точкипространства перемещает в одном и том же
направлении на одно и то же расстояние. Иначе,
если ― первоначальное, а ― смещенное
положение точки, то вектор ― один и тот же для
всех пар точек, соответствующих друг другу в
данном преобразовании.
11.
Я и моя жизнь отображается впространстве голографически.
(принцип слоеного пирога)










 mathematics
mathematics








