Similar presentations:
Tanımlayıcı Ölçütler
1. Tanımlayıcı Ölçütler
Üzerinde durulan bir çalışmada amaç;elde edilen veri setini bir ya da birkaç
ölçü ile özetlemektir. Kullanılan her
ölçü dağılımın bir özelliğini belirtir.
2. Frekans dağılımlarını tanımlayıcı özellikler iki genel başlık altında toplanır.
Yer gösterici ÖlçülerYaygınlık Ölçüleri
Ortalama
Ortanca
Tepe değeri
Standart sapma
Varyans
Varyasyon katsayısı
Standart hata
3. 1- Yer Gösterici Ölçüler
A- Ortalamalar: Dağılımın orta noktasını gösteren,dağılımı oluşturan bireylerin değerlerini tek bir
değerle temsil edilmesini sağlayan ölçüdür.
i. Aritmetik Ortalama
ii. Harmonik Ortalama
iii. Geometrik ortalama
4. Aritmetik Ortalama
i- Sınıflandırılmamış Verilerde:Denek değerlerinin toplamının denek
sayısına bölümü ile elde edilir.
n
x
X i 1
n
i
Aşırı değerlerden etkilenir.
5. Örnek: New Castle hastalığına yakalanan tavuklarda TSH hormonunun miktarındaki değişimi incelemek için 10 hasta 10 sağlam tavuk
incelenmiş olsun,ortalama
• Hasta
: 8 7 7 7 8 8 8 26 8 8
• Sağlam : 8 9 7 8 7 7 9 8 7 7
9,5
7,7
İlk bakışta hasta tavuklarda TSH hormonunun yüksek
olduğu görülmekle birlikte 26 değeri atıldıktan sonra
hasta grubun ortalaması 7,7 değerine düşmekte ve
sağlam grupla arasındaki fark önem göstermemektedir.
26 yerine 9 değeri yazılırsa, hasta grubun ortalaması 7,8
olur ve yine sağlam grupla olan farklılık önem
göstermemektedir.
6. ii- Sınıflandırılmış Verilerde Aritmetik Ortalama
nå f ´b
i
x = A + c ´ i=1
i
n
Burada
b: Çalışma birimi
fi: i. Sınıfın frekansı
A: çalışma biriminde 0’a karşılık gelen sınıfın sınıf değeri
n: Denek Sayısı
7. Örnek Bir çiftlikteki koyunların beden uzunluklarının sınıflandırımış tablosu verilmiştir. Sınıflandırılmış bu veriye göre
aritmetik ortalama nedir?Uzunluk
fi
bi
fi bi
147-151
152-156
157-161
162-166
167-171
172-176
177-182
340
430
467
233
52
16
4
-2
-1
0
1
2
3
4
-680
-430
0
233
104
48
16
1542
-709
8.
709x 159 5
156.70
1542
9. Ortanca (Medyan)
• Ortanca dağılımın orta noktasındaki değerolarak adlandırılır.
• Ortanca, dağılımdaki aşırı değerlerden
etkilenmez.
• Dağılımdaki değerler küçükten büyüğe
veya büyükten küçüğe doğru sıralanarak
tam ortadaki değer bulunur.
10. i- Sınıflandırılmamış Verilerde Ortanca (Medyan)
• Hasta: 8 7 7 7 8 8 8 26 8 8
• Ortanca: 7 7 7 8 8 8 8 8 8 26
• Sağlam : 8 9 7 8 7 7 9 8 7 7
• Ortanca: 7 7 7 7 7 8 8 8 9 9
• n sayısı çift ise n/2 ile(n+2)/2’ci değerlerin
ortalaması dağılımın ortancasıdır.
• n sayısı tek ise (n+1)/2’ci değer ortancadır
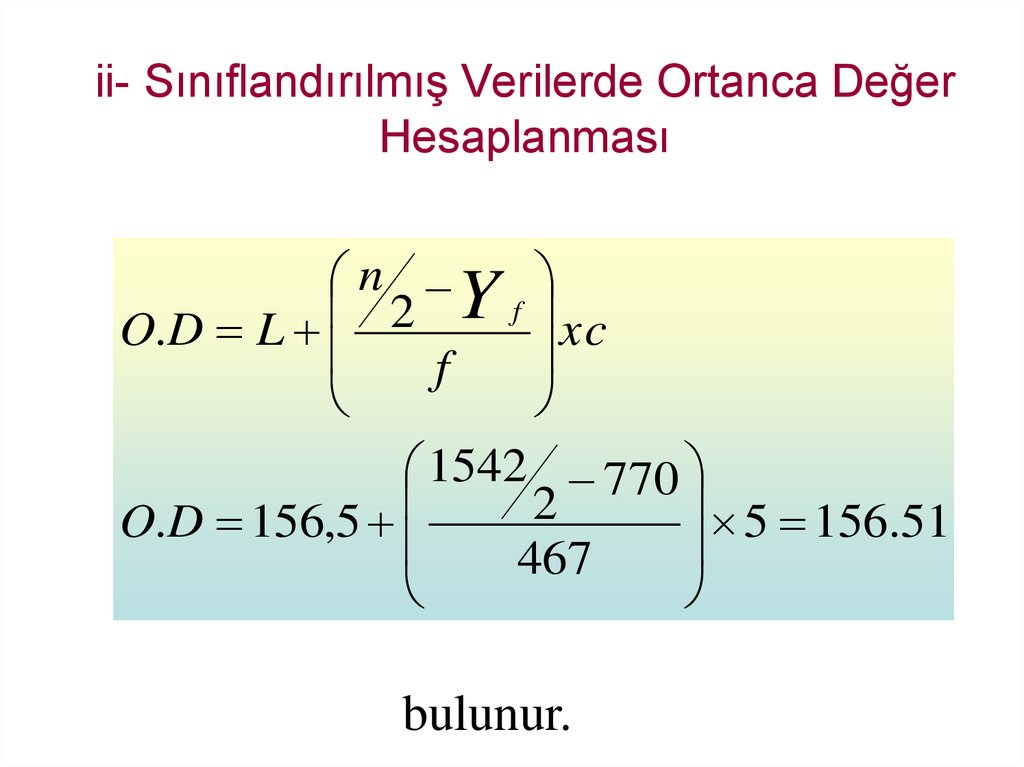
11. ii- Sınıflandırılmış Verilerde Ortanca Değer Hesaplanması
nY
f
2
O.D L
xc
f
1542 770
2
O.D 156,5
5 156.51
467
bulunur.
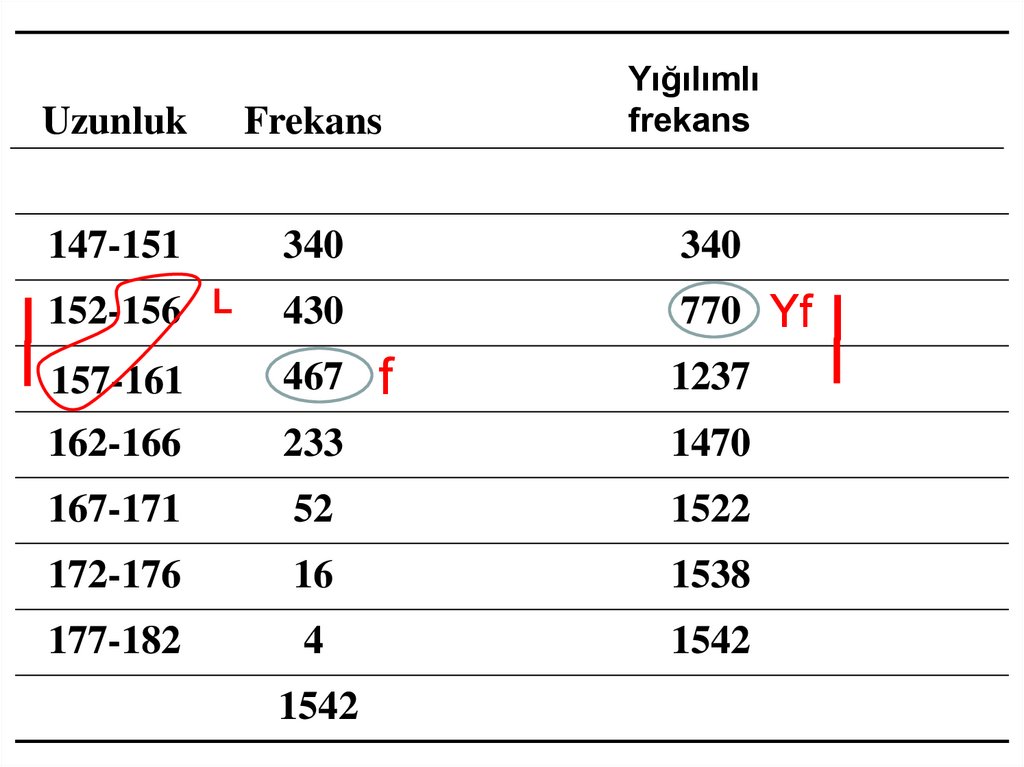
12.
UzunlukFrekans
Yığılımlı
frekans
147-151
340
340
152-156 L
430
770 Yf
157-161
467
162-166
233
1470
167-171
52
1522
172-176
16
1538
177-182
4
1542
1542
f
1237
13. Tepe Değeri Tepe değeri dağılımda en fazla tekrar edilen değerdir. Veriyi sınıflandırdığımızda, çoğunlukla en yüksek frekansa
sahip tek bir sınıf vardır.En yüksek frekansa sahip tek bir sınıfın olduğu
dağılımlara tek tepeli dağılım denir.
Bu durumda tepe değeri frekansı en fazla olan
sınıfın sınıf değeridir.
Tek tepeli dağılımlarda tepe değeri ile aritmetik
ortalama arasındaki fark büyüdükçe dağılımın
çarpıklığı artar. Bir dağılımda birden çok tepe
değeri olabilir.
14.
Uzunlukfi
147-151
152-156
157-161
162-166
167-171
172-176
177-182
340
430
467
233
52
16
4
Burada
Tepe değeri=(157+161)/2
=159
bulunur.
15. Tepe Değerinin Olumsuz Yönleri 1- Yapılan sınıflamaya göre tepe değeri değişebilir. 2- Bazı dağılımlarda tepe değeri
Tepe Değerinin Olumsuz Yönleri1-
Yapılan sınıflamaya göre tepe değeri değişebilir.
2-
Bazı dağılımlarda tepe değeri olmayabileceği gibi
bazı dağılımlarda birden fazla tepe değeri olabilir.
3-
Tepe değeri sonuç bir istatistik olup ileri
hesaplamalar için pek kullanılmaz.
16.
1614
Fre kans
12
10
8
6
4
2
0
40-44
45-49
50-54
55-59
60-64
65-69
70-74
Beslenme Bilgi Puanı
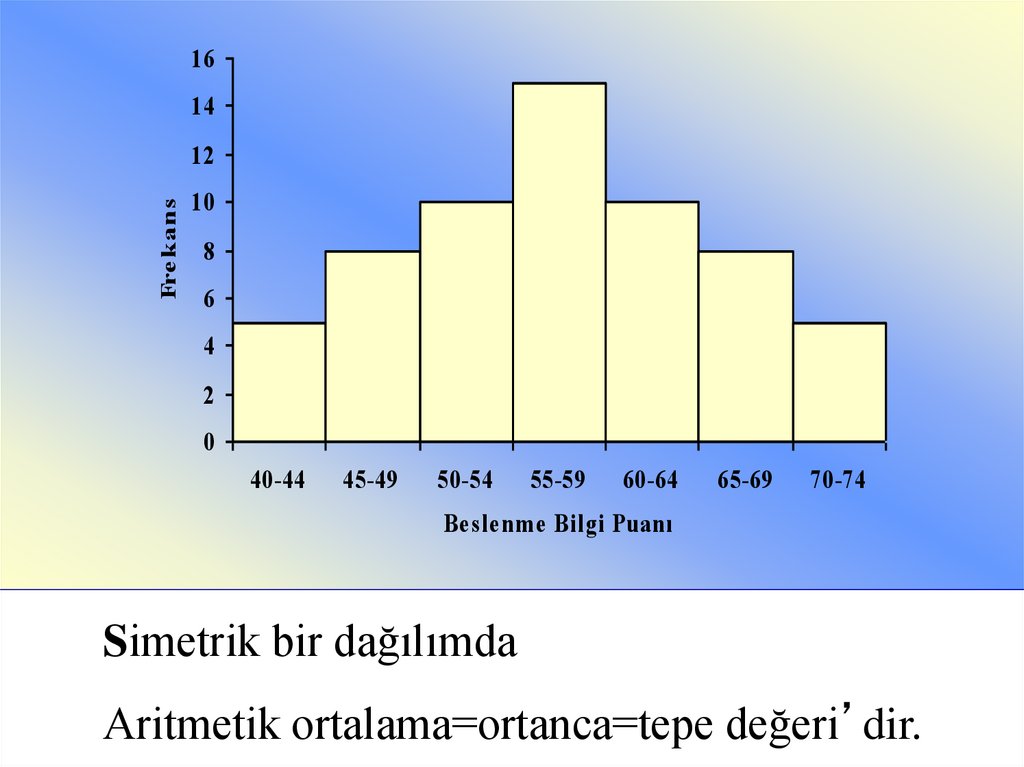
Simetrik bir dağılımda
Aritmetik ortalama=ortanca=tepe değeri’dir.
17.
4035
Frekans
30
25
20
15
10
5
0
40-44
45-49
51-54
55-59
60-64
65-69
Beslenme Bilgi Puanı
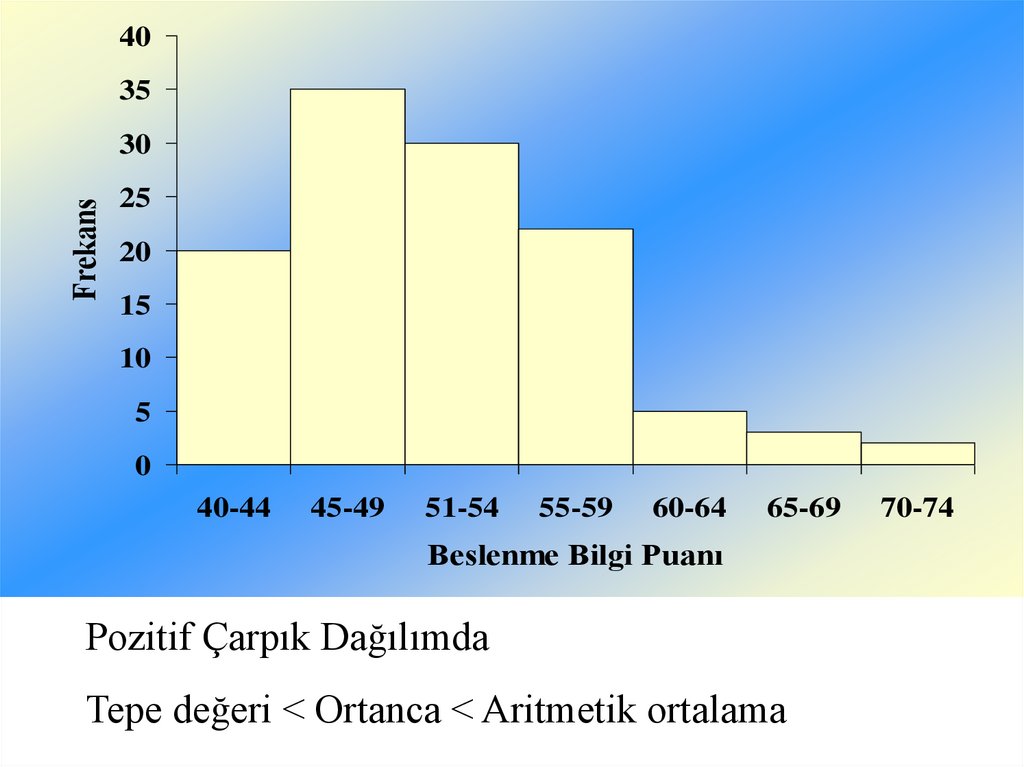
Pozitif Çarpık Dağılımda
Tepe değeri < Ortanca < Aritmetik ortalama
70-74
18.
4035
Frekans
30
25
20
15
10
5
0
40-44 45-49 51-54 55-59 60-64 65-69 70-74
Beslenme Bilgi Puanı
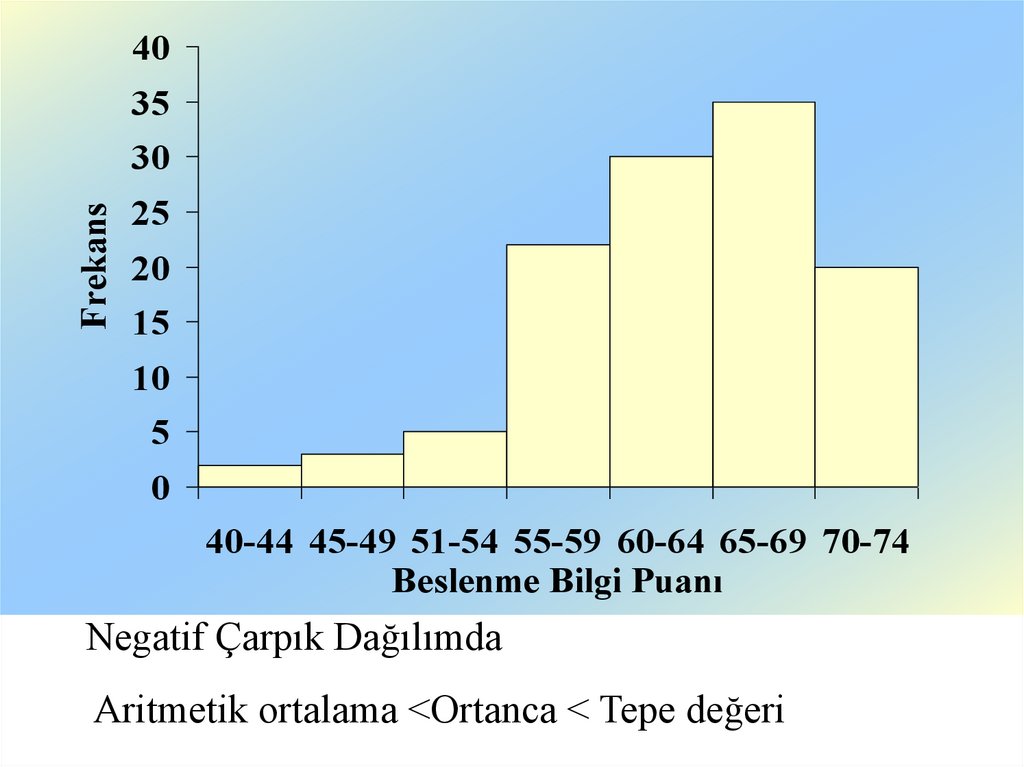
Negatif Çarpık Dağılımda
Aritmetik ortalama <Ortanca < Tepe değeri







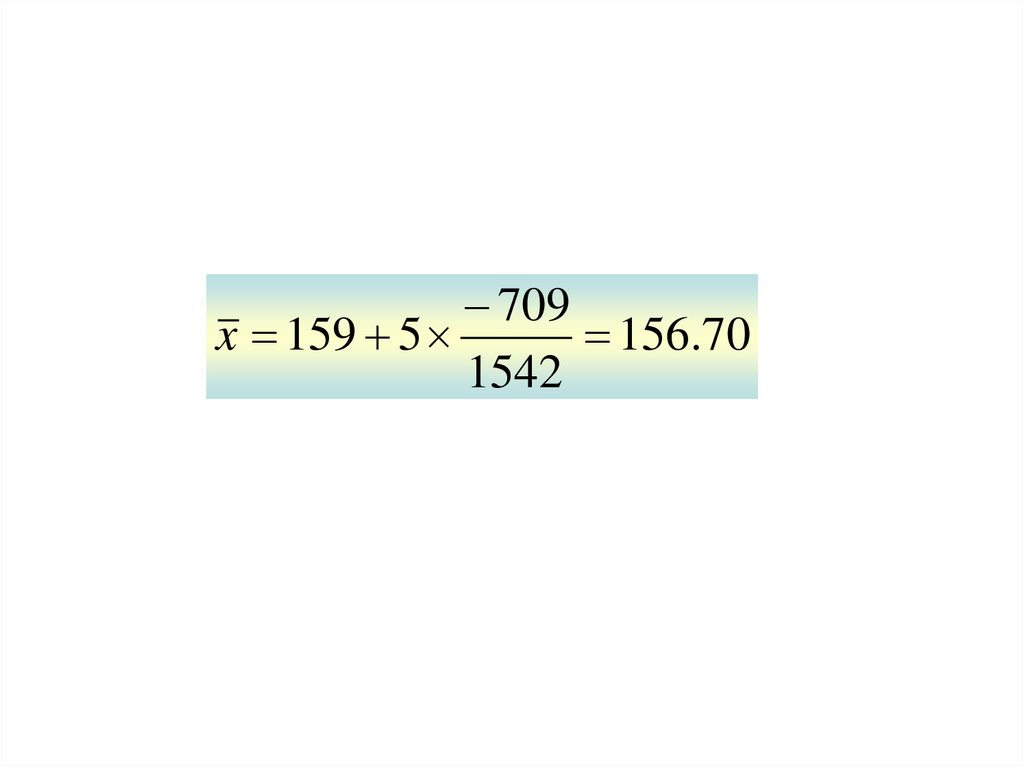





 mathematics
mathematics