Similar presentations:
Формирование ключевых и предметных компетенций при подготовке ГИА по математике
1.
ГАУ ДПО «СОИРО»Формирование ключевых и
предметных компетенций
при подготовке ГИА по математике
Клюева Татьяна Геннадьевна
www.soiro64.ru
учитель математики МАОУ «Лицей «Солярис» г.Саратов,
klyueva@solaris64.ru
2.
Математике должно учить в школе ещё стой целью, чтобы познания, здесь
приобретаемые, были достаточными для
обыкновенных потребностей в жизни.
Н.И. Лобачевский
3.
Социальные ожидания государства: становление нового работника,обладающего потребностью творчески решать сложные
профессиональные задачи.
Важнейший социальный запрос: обеспечивать подготовку
интеллектуально развитых молодых людей, способных объективно
решать социальные, профессиональные и личные проблемы.
Задача школы: развитие способностей учащегося самостоятельно
ставить учебные цели, проектировать пути их реализации,
контролировать и оценивать свои достижения, работать с разными
источниками информации, оценивать их и на этой основе
формулировать собственное мнение, суждение, оценку.
4.
Компетенция, согласно ФГОС - это способность изменять знания, уменияи личностные качества для успешной деятельности в определенной
области.
Компетенции рассматриваются как современные нормы качества
образования и имеют межпредметный системный характер, представляя
собой сочетания качеств, отношений и умений, и являются обобщенными
характеристиками специалиста.
Выделяют три составляющие компетенции:
• знание как понимание;
• знание как действие;
• знания как позиция.
Две последних компетенции и отображают деятельностную
направленность образования.
5.
Градация уровней освоенных компетенций обычно производитсяс таксономией Блума:
знание - понимание - изменение - анализ - синтез - оценка.
Привычные академические оценки системы школьного
образования
«удовлетворительно», «хорошо», «отлично» («3», «4», «5»)
можно соотнести с тремя ступенями уровней освоений:
пороговый, продвинутый, высший (2.0, 3.0, 4.0).
6.
Компетенция — способность применять знания, умения, навыки иличностные качества для успешной деятельности в различных
проблемных профессиональных либо жизненных ситуациях.
В соответствии с принятой во ФГОС классификацией компетенции
подразделяются на:
• универсальные;
• общепрофессиональные;
• профессиональные.
7.
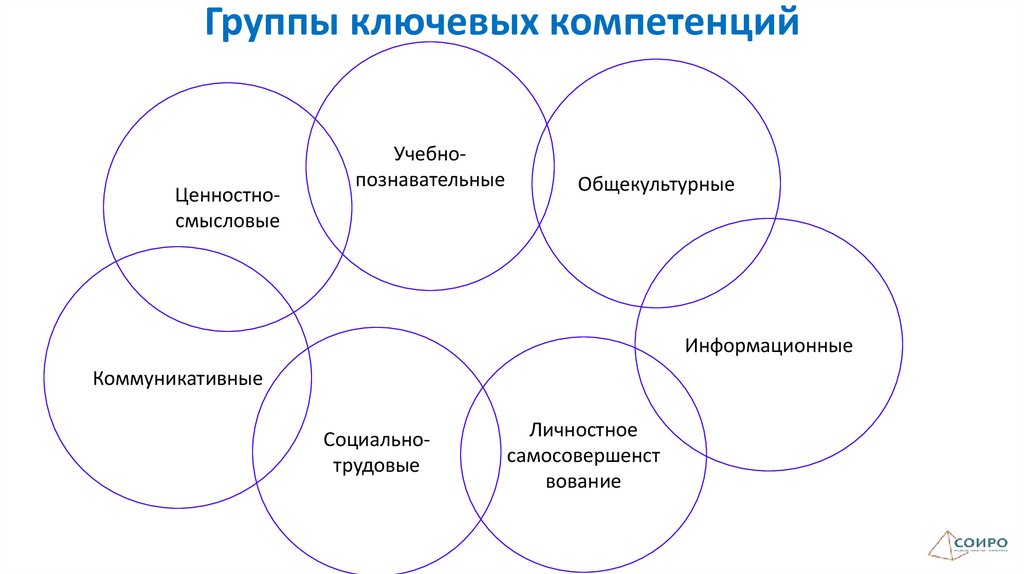
Ключевые компетенции8.
Группы ключевых компетенцийЦенностносмысловые
Учебнопознавательные
Общекультурные
Информационные
Коммуникативные
Социальнотрудовые
Личностное
самосовершенст
вование
9.
Ценностно-смысловая компетенцияРазвить способность видеть и понимать окружающий мир,
ориентироваться в нем, осознавать свою роль и предназначение,
уметь выбирать целевые и смысловые установки для своих действий
и поступков, принимать решения.
Для реализации данной компетенции подходят решения
нестандартных заданий, требующих применения учеником именно
предметной логики, а не материала из школьного курса.
10.
Общекультурная компетенцияКруг вопросов, в которых ученик должен быть хорошо осведомлен,
обладать познаниями и опытом деятельности.
Это особенности национальной и общечеловеческой культуры,
духовно-нравственные основы жизни человека и человечества,
отдельных народов, культурологические основы семейных, социальных,
общественных явлений и традиций, роль науки и религии в жизни
человека, их влияние на мир, компетенции в бытовой и культурнодосуговой сфере, владение эффективными способами организации
свободного времени.
Для реализации данной компетенции на уроке использую исторический
материал, решение задач со скрытой, неявной информативной частью.
11.
Учебно-познавательная компетенцияЭто совокупность компетенций ученика в сфере самостоятельной
познавательной деятельности, включающей элементы логической,
методологической, общеучебной деятельности, соотнесенной с реальными
познавательными объектами.
Сформировать знания и умения целеполагания, планирования, анализа,
рефлексии, самооценки учебно-познавательной деятельности.
Умение отличать факты от домыслов, владение измерительными навыками,
использование вероятностных, статистических и иных методов познания мира.
Создание поисковой ситуации способствует воспитанию и развитию творческих
способностей учащихся, обучению их системе активных умственных действий.
Ученик анализирует, сравнивает, синтезирует, обобщает, конкретизирует
фактический материал, сам получает из него новую информацию.
12.
Информационная компетенцияПри помощи реальных объектов и информационных технологий
формируются умения самостоятельно искать, анализировать и отбирать
необходимую информацию, организовать, преобразовать, сохранить и
передать её.
Эта компетенция обеспечивает навыки деятельности ученика с
информацией, содержащейся в учебных предметах и образовательных
областях, а также в окружающем мире.
На уроках использую ИКТ, онлайн-тестирование при подготовке к ЕГЭ.
Учащиеся принимают участие в конкурсах, олимпиадах, конференциях
различного уровня, выполняют работы по проектной методике.
13.
МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ – ЭТО…способность человека формулировать, применять и интерпретировать
математику в разнообразных контекстах.
Эта способность включает математические рассуждения, использование
математических понятий, процедур, фактов и инструментов, чтобы
описать, объяснить и предсказать явления.
Она помогает людям понять роль математики в мире, высказывать
хорошо обоснованные суждения и принимать решения, которые
необходимы конструктивному, активному и размышляющему
гражданину.
Курс «Функциональная грамотность»
14.
МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ – ЭТО…способность к пониманию и грамотному использованию
математического языка;
готовность к математической деятельности (математическому
моделированию ситуаций, описанных в задачах).
Л.Г. Петерсон
15.
ПРИОРИТЕТНАЯ ЦЕЛЬ ОБУЧЕНИЯ МАТЕМАТИКЕ В 5—9 КЛАССАХформирование функциональной
математической грамотности: умения
распознавать проявления математических
понятий, объектов и закономерностей в
реальных жизненных ситуациях и при
изучении других учебных предметов,
проявления зависимостей и закономерностей,
формулировать их на языке математики и
создавать математические модели, применять
освоенный математический аппарат для
решения практико-ориентированных задач,
интерпретировать и оценивать полученные
результаты.
16.
Алгоритм решения задач методом математического моделированияI. Построение математической модели
1.Внимательно прочитать задачу и определить, что известно и что нужно найти.
2.Проверить соответствие единиц счёта / измерения величин (при необходимости
выполнить их преобразование).
3.Установить взаимосвязи между описанными в ней величинами (можно использовать
формулы, схемы, таблицы). Если нужно, одну или несколько неизвестных величин
обозначить буквами.
4. Построить математическую модель задачи (выражение, уравнение и др.).
5. Зафиксировать искомую величину и её возможные значения.
II. Работа с математической моделью
6. Найти все решения, удовлетворяющие построенной модели.
III. Практический вывод
7. Проверить соответствие полученного ответа условию, вопросу и смыслу задачи.
17.
Алгоритм решения задач методом математического моделированияI. Построение математической модели
1. Внимательно прочитать задачу.
2. Определить, какие величины известны и какие надо найти.
3. Проверить соответствие единиц измерения величин.
4. Выбрать неизвестные величины и ввести для них буквенные обозначения.
5. Определить множество значений, которые могут принимать неизвестные величины. 6.
Установить взаимосвязи между величинами (не явно заданные в условии и возникающие из
свойств моделируемого объекта).
7. Составить уравнение и обосновать его.
8. Проверить, что каждый элемент условия задачи описан соответствующим уравнением.
9. Зафиксировать искомую величину.
II. Работа с математической моделью
10. Найти все решения, удовлетворяющие построенной модели.
III. Практический вывод
11. Проверить соответствие полученного ответа вопросу задачи.
12. Убедиться, что полученные решения соответствуют смыслу задачи.
18.
Первоначальный план решения нестандартной задачи1. Определить, что требуется найти в задаче, и понять, что представляет собой искомая
величина и какие значения она может принимать.
2. Определить, что известно.
3. Попытаться найти аналогию между решёнными ранее задачами и новой задачей, а
затем использовать уже известный способ решения.
4. Выяснить, какие данные необходимы для нахождения неизвестного, тем самым
заменить задачу поиска исходного неизвестного поиском новых неизвестных,
которые возможно будет найти уже известными способами.
5. Провести анализ данных: выяснить, что может быть определено по известным
данным.
6. Попытаться переформулировать исходную задачу, сделав её более понятной.
7. Попытаться разбить сложную задачу на несколько более простых, решение которых,
в конечном счёте, приведёт к решению исходной задачи.
19.
20.
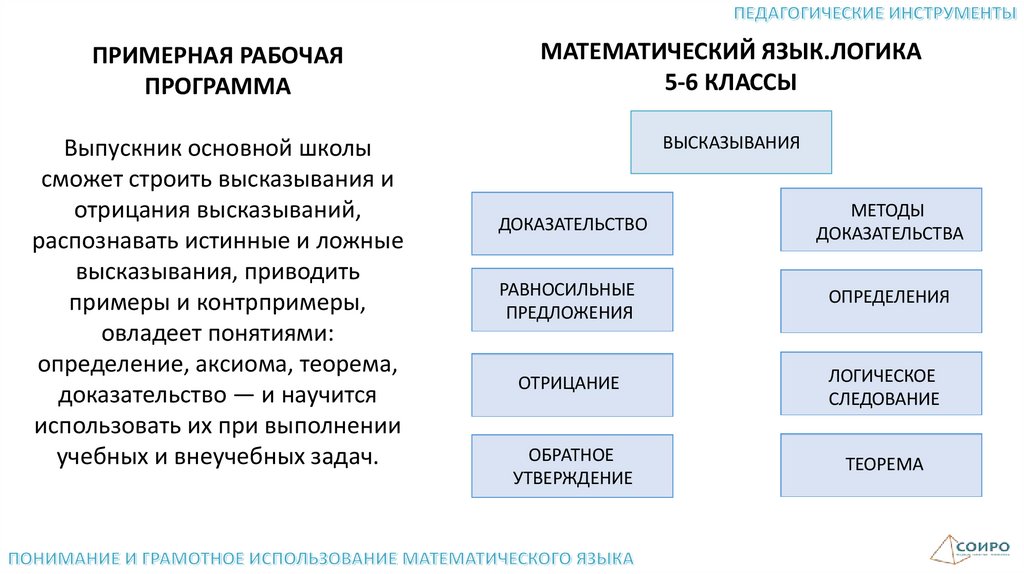
ПРИМЕРНАЯ РАБОЧАЯПРОГРАММА
МАТЕМАТИЧЕСКИЙ ЯЗЫК.ЛОГИКА
5-6 КЛАССЫ
Выпускник основной школы
сможет строить высказывания и
отрицания высказываний,
распознавать истинные и ложные
высказывания, приводить
примеры и контрпримеры,
овладеет понятиями:
определение, аксиома, теорема,
доказательство — и научится
использовать их при выполнении
учебных и внеучебных задач.
ВЫСКАЗЫВАНИЯ
ДОКАЗАТЕЛЬСТВО
МЕТОДЫ
ДОКАЗАТЕЛЬСТВА
РАВНОСИЛЬНЫЕ
ПРЕДЛОЖЕНИЯ
ОПРЕДЕЛЕНИЯ
ОТРИЦАНИЕ
ЛОГИЧЕСКОЕ
СЛЕДОВАНИЕ
ОБРАТНОЕ
УТВЕРЖДЕНИЕ
ТЕОРЕМА
21.
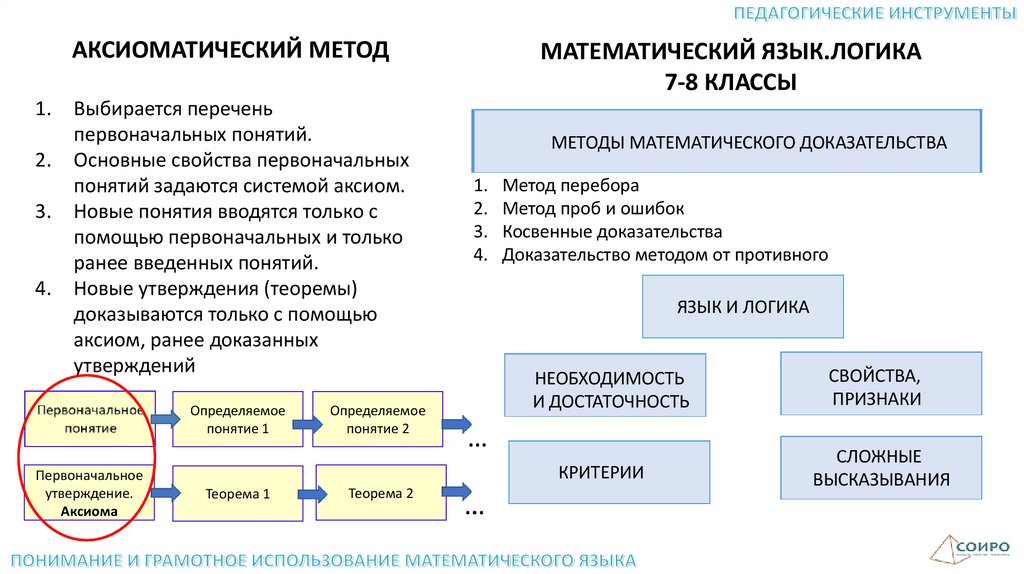
АКСИОМАТИЧЕСКИЙ МЕТОД1.
2.
3.
4.
Выбирается перечень
первоначальных понятий.
Основные свойства первоначальных
понятий задаются системой аксиом.
Новые понятия вводятся только с
помощью первоначальных и только
ранее введенных понятий.
Новые утверждения (теоремы)
доказываются только с помощью
аксиом, ранее доказанных
утверждений
Определяемое
понятие 1
Первоначальное
утверждение.
Аксиома
Теорема 1
Определяемое
понятие 2
Теорема 2
МАТЕМАТИЧЕСКИЙ ЯЗЫК.ЛОГИКА
7-8 КЛАССЫ
МЕТОДЫ МАТЕМАТИЧЕСКОГО ДОКАЗАТЕЛЬСТВА
1.
2.
3.
4.
Метод перебора
Метод проб и ошибок
Косвенные доказательства
Доказательство методом от противного
ЯЗЫК И ЛОГИКА
НЕОБХОДИМОСТЬ
И ДОСТАТОЧНОСТЬ
СВОЙСТВА,
ПРИЗНАКИ
КРИТЕРИИ
СЛОЖНЫЕ
ВЫСКАЗЫВАНИЯ
…
22.
Принципы подготовки к ГИА по математикетематический
логический
тренировочный
индивидуальный
временной
контролирующий
23.
Формы и методы работы при подготовке к ГИА по математикеПсихолого-педагогическая диагностика
Работа с родителями, обратная связь
Информационный стенд
Стартовые, диагностические, тренировочные работы, анализ результатов, работа по
корреции
Дополнительные занятия по подготовке к ГИА
Устная работа на уроках, тренинги, зачёты
Включение в изучение текущего учебного материала заданий. соответствующих
экзаменационным заданиям
Использование в домашних заданиях материалов открытого банка ОГЭ, ЕГЭ
Включение экзаменационных задач в содержание текущего контроля
Опорные конспекты, схемы, алгоритмы, тетради для формул
Тематическое повторение материала в течение года
Междисциплинарные проекты, задачи
Индивидуальные папки, маршруты учащихся, мониторинг
Заполнение бланков
24.
Формирование компетентности учащихся на различных этапах урокаЭтапы урока
Цель, результативность
Виды деятельности
Проверка
домашнего задания
Цель: помочь учащимся активировать умственную деятельность, развивать критическое
мышление, учить оценивать знания учеников.
Результативность: формирование познавательной компетентности
Цель: создать условия для развития самостоятельности мышления, для формирования
гибкости и точности мысли, развития внимания и памяти.
Результативность: формирование самообразовательной компетентности
Рецензирование ответов (домашнего задания)
Цель: содействовать развитию у школьников умений использовать научные методы
познания (наблюдение, гипотеза, эксперимент).
Результативность: формирование исследовательской компетентности
Цель: создать условия для развития у школьников умений формулировать проблемы,
предлагать пути их решения
Результативность: формирование информационной компетентности
Цель: помочь детям научиться применять знания, оперировать знаниями, содействовать
развитию гибкости использования знаний
Результативность: формирование исследовательской, самообразовательной
компетентностей
Вывод формул, правил
Цель: создать условия для изучения свойств, правил
Результативность: формирование познавательной компетентности
Цель: организовать деятельность учащихся для закрепления умения решать задачи и
примеры, содействовать формированию умения проверять, слушать, думать.
Результативность: формирование познавательной компетентности
Цель: обеспечит развитие личной позиции учеников, опираясь на их знание темы
Результативность: формирование интеллектуально-познавательной компетентности
Цель: помочь детям при работе с информацией, обеспечить закрепление знаний текста,
понимание темы
Результативность: формирование коммуникативной и познавательной компетентности
Самостоятельная работа частично-поискового,
исследовательского характера.
Компетентностно-ориентированные задания.
Решения задач, примеров с
комментированием, индивидуальная работа с
самопроверкой, игровые формы.
Решение задач несколькими способами.
Работа с учебником (учебная практическая
работа)
Изучение нового
материала
Закрепление,
тренировка,
отработка умений и
навыков
Математический диктант, тест, самостоятельная
работа (по материалу домашнего задания с
ограничением времени решения)
Проблемная лекция с использованием
приобретенной учениками информации
Экспериментальная работа
Практическая работа
25.
Формирование компетентности учащихся на различных этапах урокаЭтапы урока
Цель, результативность
Виды деятельности
Творческая работа
Цель: организовать деятельность учащихся по созданию проектов на основе
изученного материала
Результативность: формирование исследовательской компетентности
Цель: создать условия для развития воображения и умения
абстрагироваться.
Результативность: формирование самообразовательной, исследовательской
компетентности
Создание проектов
Контроль
Цель: организовать самостоятельную работу
Результативность: формирование самообразовательной, социальной
компетентности
Цель: обеспечит проверку усвоения материала, формирования умения
подбирать примеры
Результативность: формирование самообразовательной компетентности
Разноуровневая самостоятельная
работа (взаимопроверка, самопроверка,
контроль учителя)
Составить вопросы, задачи и примеры
по теме урока
Домашнее
задание
Цель: развивать умение самоконтроля и взаимоконтроля
Результативность: формирование интеллектуально-познавательной
компетентности
Разноуровневые задачи, задачи
исследовательского характера,
творческие задания
Работ в группах со взаимной оценкой
26.
Задача.Четырехметровая газовая труба проржавела в
двух местах. Определить вероятность того, что все
три получившиеся части можно будет
использовать в качестве отводов к газовым
плитам. Если по нормативам плита не должна
находиться на расстоянии ближе 1 м от
магистральной газовой трубы.
27.
Задача.Четырехметровая газовая труба проржавела в двух местах. Определить вероятность
того, что все три получившиеся части можно будет использовать в качестве отводов
к газовым плитам. Если по нормативам плита не должна находиться на расстоянии
ближе 1 м от магистральной газовой трубы.
Решение.
4м=400 см
У
х
у
х ≥ 100,
у ≥ 100,
400-х-у ≥ 100.
400
300
Р= S (1)/S(2)
Р=k² =1/4
P=1/16=0,0625
200
100
Ответ: 0,0625.
0
100
200
300
400
Х
400-х-у























 mathematics
mathematics








