Кодирование информации при передаче по дискретному каналу без помех

1.

ПЛАН:
7. Кодирование информации при передаче по дискретному каналу без помех
7.1. Эффективное кодирование
7.1.1. Код Шеннона-Фано
7.1.2. Код Хаффмана
7.2. Префиксные коды
7.3. Недостатки системы эффективного кодирования
7.5. Эффективное кодирование при неизвестной статистике сообщений
7.6. Код Хемминга

2.

Кодирование информации при передаче по дискретному каналу без помех

3.

Кодирование
Суть самой процедуры кодирования (любой).
Любое дискретное сообщение xi из алфавита источника A{ xi } объемом в K символов можно
закодировать последовательностью соответствующим образом выбранных кодовых символов xj из
алфавита
{ xj }.
Например, любое число (а xi можно считать числом) можно записать в заданной позиционной
системе счисления следующим образом:
xi = an-1 X n-1 + an-2 X n-2 +… + a0 X 0, где X - основание системы счисления; a0 … an-1 коэффициенты при имеющие значение от 0 до X - 1.
Пусть, к примеру, значение xi = 59 , тогда его код по основанию X = 8, будет иметь вид
xi = 59 = 7·81 + 3·80 =738 .
Код того же числа, но по основанию X = 4 будет выглядеть следующим образом:
xi = 59 = 3·42 + 2·41+ 3·40 = 3234 .
Наконец, если основание кода X= 2, то
xi = 59 = 1·25 + 1·24 + 1·23 + 0·22 + 1·21 + 1·20 = 1110112 .
Таким образом, числа 73, 323 и 111011 можно считать, соответственно, восьмеричным,
четверичным и двоичным кодами числа M = 59.
В принципе основание кода может быть любым, однако наибольшее распространение
получили двоичные коды, или коды с основанием 2, для которых размер алфавита кодовых
символов { xj } равен двум, xj Ↄ 0,1. Двоичные коды, то есть коды, содержащие только нули и
единицы, очень просто формируются и передаются по каналам связи и, главное, являются
внутренним языком цифровых ЭВМ, то есть без всяких преобразований могут обрабатываться
цифровыми средствами. Поэтому, когда речь идет о кодировании и кодах, чаще всего имеют в виду
именно двоичные коды. В дальнейшем будем рассматривать в основном двоичное кодирование.

4.

Кодирование
Самый простой способ представления или задания кодов - кодовые таблицы, ставящие в соответствие
сообщениям xi соответствующие им коды (cм. табл. 7.1.)
Таблица 7.1
Буква xi
Число xi
А
Б
В
Г
Д
Е
Ж
З
0
1
2
3
4
5
6
7
Код с основанием
10
Код с основанием 4
0
1
2
3
4
5
6
7
00
01
02
03
10
11
12
13
Код с основанием 2
000
001
010
011
100
101
110
111
Другой способ - представление их в виде кодового дерева (рис. 7.1). Для того, чтобы построить кодовое дерево
для данного кода, начиная с некоторой точки - корня кодового дерева - проводятся ветви - 0 или 1. На вершинах
кодового дерева находятся буквы алфавита источника, причем каждой букве соответствуют своя вершина и свой
путь от корня к вершине. К примеру, букве А соответствует код 000, букве В – 010, букве Е – 101 и т.д. Код,
полученный с использованием кодового дерева, изображенного на рис. 7.1, является равномерным трехразрядным
кодом. Равномерные коды очень широко используются в силу своей простоты и удобства процедур кодированиядекодирования: каждой букве – одинаковое число бит; принял заданное число бит – ищи в кодовой таблице
соответствующую букву.
Корень
Узлы
АБ
12
В
3
Г
4
Д
5
Е
6
Ж
7
З
8
0
0
1
0
0
1
Вершина
1
0
1
1
1
0
0
Рис. 7.1. Графическое представление
кодового дерева
1

5.

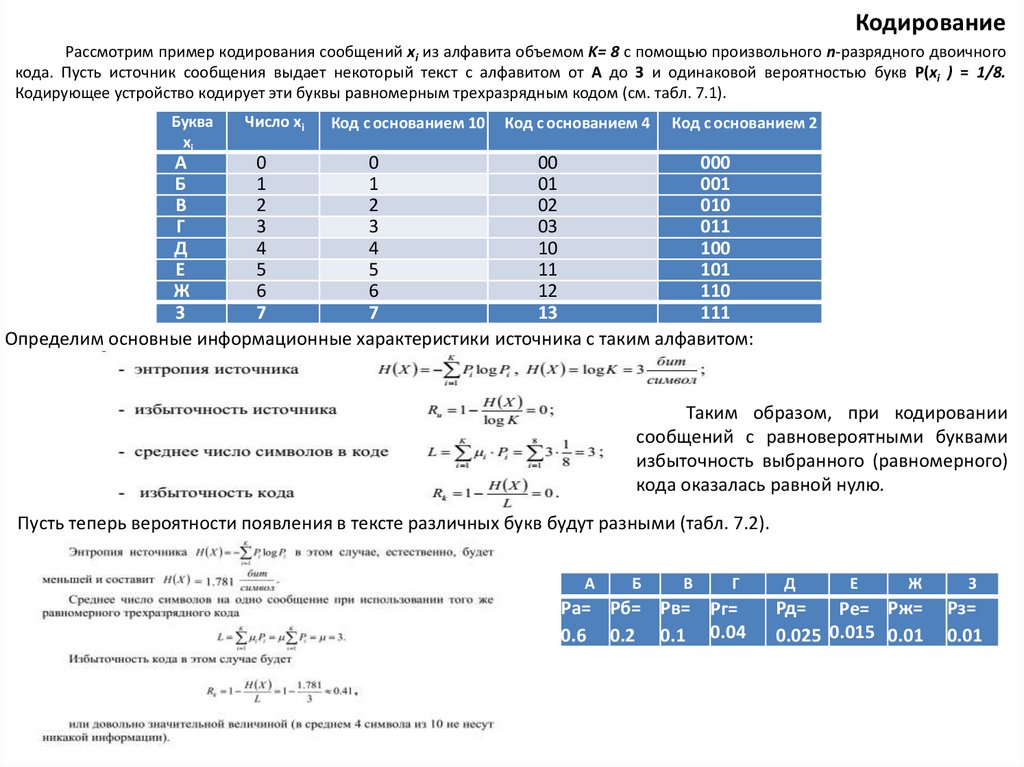
Кодирование
Рассмотрим пример кодирования сообщений xi из алфавита объемом K= 8 с помощью произвольного n-разрядного двоичного
кода. Пусть источник сообщения выдает некоторый текст с алфавитом от А до З и одинаковой вероятностью букв Р(xi ) = 1/8.
Кодирующее устройство кодирует эти буквы равномерным трехразрядным кодом (см. табл. 7.1).
Буква
xi
Число xi
Код с основанием 10
Код с основанием 4
Код с основанием 2
А
0
0
00
000
Б
1
1
01
001
В
2
2
02
010
Г
3
3
03
011
Д
4
4
10
100
Е
5
5
11
101
Ж
6
6
12
110
З
7
7
13
111
Определим основные информационные характеристики источника с таким алфавитом:
Таким образом, при кодировании
сообщений с равновероятными буквами
избыточность выбранного (равномерного)
кода оказалась равной нулю.
Пусть теперь вероятности появления в тексте различных букв будут разными (табл. 7.2).
А
Б
В
Г
Ра= Рб= Рв= Рг=
0.6 0.2 0.1 0.04
Д
Е
Ж
З
Рд=
Ре= Рж=
0.025 0.015 0.01
Рз=
0.01

6.

Эффективное кодирование
Операция кодирования тем более эффективна (экономична), чем меньшей длины кодовые
слова сопоставляются сообщениям. Поэтому за характеристику эффективности кода примем
среднюю длину кодового слова:
При установлении оптимальных границ для L исходят из следующих соображений:
1. количество информации, несомое кодовым словом, не должно быть меньше количества
информации, содержащегося в соответствующем сообщении, иначе при кодировании будут
происходить потери в передаваемой информации;
2. кодирование будет тем более эффективным, чем большее количество информации будет
содержать в себе каждый кодовый сим- вол. Это количество информации максимально, когда
все кодовые символы равновероятны, и равно log m. При этом i-е кодовое слово будет нести
количество информации, равное mi log m.
Теорема (сформулирована Шенноном). При кодировании сообщений xi в алфавите,
насчитывающем
m
символов,
при
условии
отсутствия
шумов, средняя длина кодового слова не может быть меньше, чем
L ≥ H(X)/ log m (7.2), где H(X) – энтропия сообщения.

7.

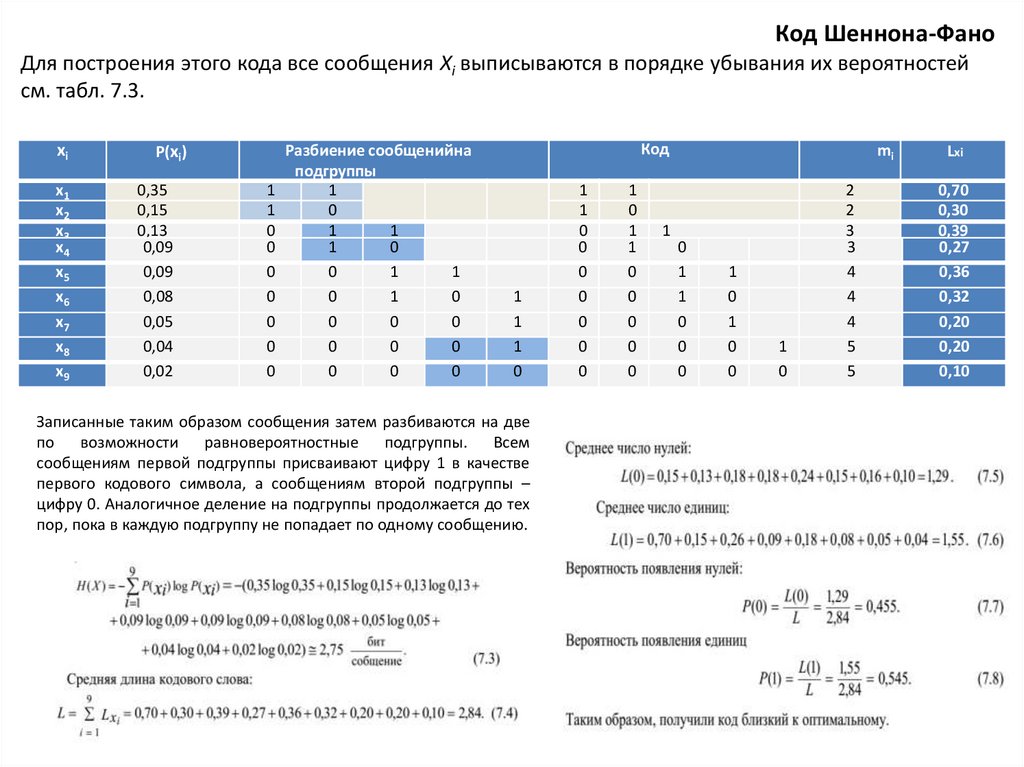
Код Шеннона-Фано
Для построения этого кода все сообщения Xi выписываются в порядке убывания их вероятностей
см. табл. 7.3.
xi
x1
x2
x3
x4
x5
x6
x7
x8
x9
P(xi)
0,35
0,15
0,13
0,09
0,09
0,08
0,05
0,04
0,02
Разбиение сообщенийна
подгруппы
1
1
1
0
0
1
1
0
1
0
0
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
Код
1
1
1
0
Записанные таким образом сообщения затем разбиваются на две
по возможности равновероятностные
подгруппы. Всем
сообщениям первой подгруппы присваивают цифру 1 в качестве
первого кодового символа, а сообщениям второй подгруппы –
цифру 0. Аналогичное деление на подгруппы продолжается до тех
пор, пока в каждую подгруппу не попадает по одному сообщению.
1
1
0
0
0
0
0
0
0
1
0
1
1
0
0
0
0
0
1
mi
0
1
1
0
0
0
1
0
1
0
0
1
0
2
2
3
3
4
4
4
5
5
Lxi
0,70
0,30
0,39
0,27
0,36
0,32
0,20
0,20
0,10

8.

Пусть имеется случайная величина
вероятностей
X(x1,x2,x3,x4,x5,x6,x7,x8), имеющая восемь состояний
с распределением
Для кодирования алфавита из восьми букв без учета вероятностей равномерным двоичным кодом нам понадобятся
три позиции символов:
Это
000, 001, 010, 011, 100, 101, 110, 111
Чтобы ответить, хорош этот код или нет, необходимо сравнить его с оптимальным значением, то есть определить
энтропию
Определив избыточность L по формуле L=1-H/H0=1-2,75/3=0,084,
кода на 8,4%.
Закодируем буквы алфавита в коде Шеннона-Фано.
Все буквы записываются в порядке убывания их
вероятностей, затем делятся на равновероятные группы,
которые обозначаются 0 и 1, затем вновь делятся на
равновероятные группы и т.д.
Средняя длина полученного кода будет равна
Итак, мы получили оптимальный код. Длина этого кода
совпала с энтропией. Данный код оказался удачным, так как
величины вероятностей точно делились на равновероятные
группы.
видим, что возможно сокращение длины

9.

Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит
включен и пробел, частота которого составляет 0,145. Метод кодирования представлен
в таблице
Средняя
равна,
длина
данного
кода
бит/букву;
будет
Энтропия
H=4.42 бит/буква.
Эффективность
полученного кода можно определить как отношение
энтропии к средней длине кода. Она равна 0,994.
При значении равном единице код является
оптимальным. Если бы мы кодировали кодом
равномерной длины
то эффективность была бы значительно ниже.

10.

11.

Код Хаффмана
Для получения кода Хаффмана все сообщения выписывают в порядке убывания вероятностей. Две
наименьшие вероятности объединяют скобкой (табл. 7.4) и одной из них присваивают символ 1, а другой – 0.
Затем эти вероятности складывают, результат записывают между двумя вероятностями.
Процесс
объединения двух сообщений с наименьшими вероятностями продолжают до тех пор, пока суммарная
вероятность двух оставшихся сообщений не станет равной единице. Код для каждого сообщения строится при
записи двоичного числа справа налево путем обхода по линиям вверх направо, начиная с вероятности
сообщения, для которого строится код.
Средняя длина кодового слова (табл. 7.4) L = 2,82, что несколько меньше, чем в коде Шеннона-Фано (L = 2,84).

12.

13.

14.

15.

16.

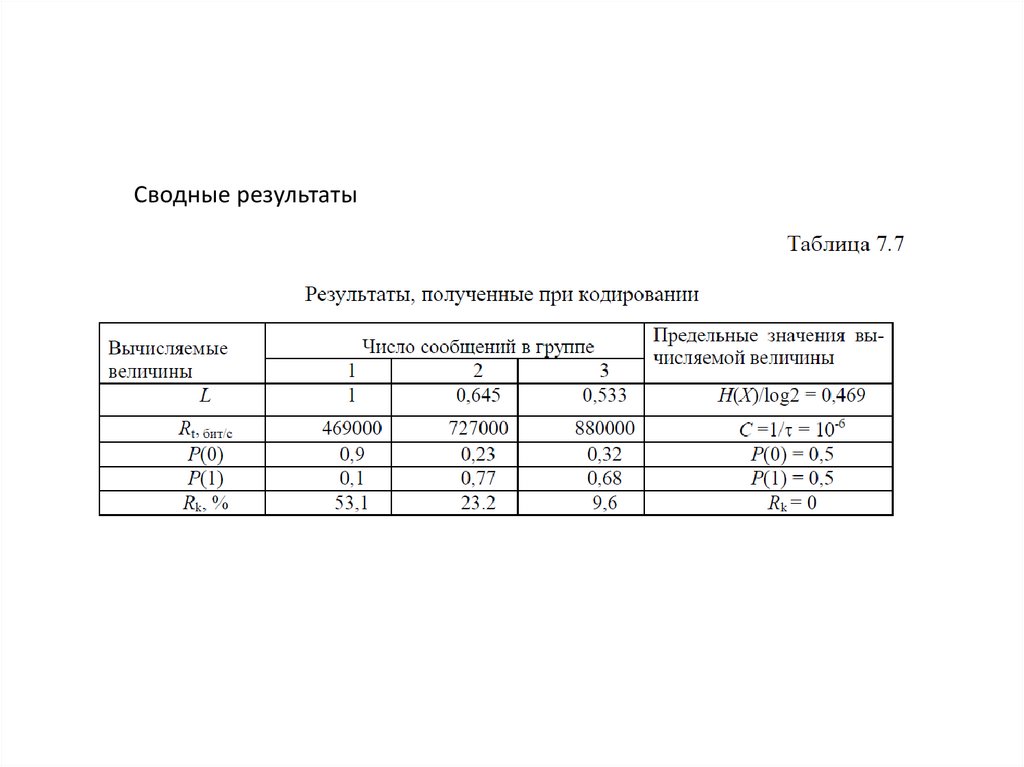
Сводные результаты

17.

Построение кода Хаффмана (то же самое, только подробнее)
Шаг 1. Символы алфавита, составляющего сообщение, выписываются в основной столбец в
порядке убывания вероятностей. Два последних символа объединяются в один вспомогательный,
которому приписывается суммарная вероятность.
Шаг 2. Вероятности символов, не участвовавших в объединении, и полученная суммарная
вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две
последних объединяются. Процесс продолжается до тех пор, пока не получим единственный
вспомогательный символ с вероятностью, равной единице. Эти два шага алгоритма иллюстрирует
таблица 4 для уже рассмотренного случая кодирования восьми символов.
Шаг 3. Строится кодовое дерево, и формируются кодовые слова, соответствующие кодируемым
символам. Для составления кодовой комбинации, соответствующей данному сообщению,
необходимо проследить путь перехода сообщений по строкам и столбцам таблицы. Для наглядности
строится кодовое дерево (рис.7.4). Из точки, соответствующей вероятности 1, направляются две ветви.
Ветви с большей вероятностью присваивается символ 1, а с меньшей - символ 0. Такое
последовательное ветвление продолжаем до тех пор, пока не дойдем до каждого символа.

18.

Рис.7.4 Кодовое дерево
Символам источника сопоставляются концевые вершины
дерева.
Кодовые
слова,
соответствующие
символам,
определяются путями из начального узла дерева к финальным.
Каждому ответвлению влево соответствует символ 1 в
результирующем коде, а вправо - символ 0. Ни одно кодовое
слово не будет началом другого, т.к. только концевым вершинам
кодового дерева сопоставляются кодовые слова. Таким образом
гарантируется возможность разбиения последовательности
кодовых слов на отдельные кодовые слова.
Двигаясь по кодовому дереву сверху вниз можно записать
для каждой буквы соответствующую ей кодовую комбинацию
Пример. Возьмем сообщение, состоящее из 6 символов.
Например, а2 а3 а1 а1 а4 а2 .Тогда код сообщения приобретает
следующий вид:
Возможный способ декодирования представлен на таблице:

19.

20.

Префиксные коды
Целесообразно обеспечить однозначное декодирование без введения дополнительных символов. Для этого
эффективный код необходимо строить так, чтобы ни одна комбинация кода не совпадала с началом более длинной
комбинации. Коды, удовлетворяющие этому условию, называют префиксными кодами. Последовательность
100000110110110100 комбинаций префиксного кода, например,

21.

Недостатки системы эффективного кодирования
1. Различие в длине кодовых комбинаций.
Если моменты снятия информации с источника неуправляемы, кодирующее устройство через
равные промежутки времени выдает комбинации различной длины. Так как линия связи
используется эффективно только в том случае, когда символы поступают в нее с постоянной
скоростью, то на выходе кодирующего устройства должно быть предусмотрено буферное
устройство. Оно запасает символы по мере поступления и выдает их в линию связи с постоянной
скоростью. Аналогичное устройство необходимо и на приемной стороне. Второй недостаток связан
с возникновением задержки в передаче информации. Наибольший эффект достигается при
кодировании длинными блоками, а это приводит к необходимости накапливать знаки, прежде чем
поставить им в соответствие определенную последовательность символов. При декодировании
задержка возникает снова. Общее время задержки может быть велико, особенно при появлении
блока, вероятность которого мала. Это следует учитывать при выборе длины кодируемого блока.
2. Специфическое влиянии помех на достоверность приема.
Одиночная ошибка может перевести передаваемую кодовую комбинацию в другую, не равную
ей по длительности. Это повлечет за собой неправильное декодирование ряда последующих
комбинаций, которые называют треком ошибки.
Специальными методами построения эффективного кода трек ошибки стараются свести к
минимуму.
Следует отметить относительную сложность технической реализации систем эффективного
кодирования.
Методы эффективного кодирования Шеннона-Фано, Хаффмана позволяют производить
кодирование, если известна статистика входных сообщений, т.е. известна вероятность их появления
p(xi).

22.

Эффективное кодирование при неизвестной статистике сообщений
Коды, эффективные одновременно для некоторого класса источников, называют
универсальными кодами.
Предположим,
что
алфавит
состоит
из
двух
X1 и X2, появляющихся независимо, с вероятностями p и g = 1-p. Однако величина р
заранее неизвестна. Требуется построить код, для которого среднее число символов
«0» и «1» на одну букву алфавита приближалось бы к H(X) при любом р, 0 <= p <= 1.
Этот код строится так. Множество всех блоков длины n в алфавите X разбиваем
на группы, которые имеют одинаковые вероятности при любом p. Таких групп будет
n+1. В нулевой группе отсутствует буква X2, она состоит из единственного блока
X1X1X1…X1, вероятность появления которого p n .
Первая группа состоит из блоков длиной n, содержащих одну букву X2. Эта группа
cостоит из C 1 n = n блоков, вероятность каждого из которых равна P n - 1 *g . Группы с
номером k состоят из всех блоков длиной n, содержащих k букв X2. Эта группа содержит
n блоков, вероятность каждого из которых p n - k *g k .
Универсальный код для k-й группы состоит из двух частей: префикса и
суффикса. Префикс содержит log(n+1) двоичных знаков. Префикс указывает, к какой
группе сообщений принадлежит кодируемый блок, суффикс содержит log Ckn
двоичных символов и указывает номер блока в группе.
Построенный таким образом код будет однозначно дешифрируем. На приемном
конце первоначально по log(n+1) элементам кода определяют, к какой группе
принадлежит переданное сообщение, а затем по следующим log Ckn элементам
определяют, какое именно сообщение передавалось.

23.

Эффективное кодирование при неизвестной статистике сообщений
Код в табл. 7.8 построен описанным выше способом.
Здесь выделены штриховой линией префиксы

24.

Эффективное кодирование при неизвестной статистике сообщений
Опишем алгоритм нахождения суффикса. Пусть в блоке X длиной n буква X1
встречается на местах i1,i2,…,ir, тогда суффиксом для X назовем число N(x),
вычисляемое по правилу

25.

26.

2
КОД ХЭММИНГА
Линейные и систематические коды
Систематическими называют такие коды, в которых информационные и
корректирующие символы расположены по строго определенной системе
и всегда занимают строго определенные места в кодовых комбинациях.
несистематический, разделимый
код
m
k =n
систематический, неразделимый
код

27.

3
КОД ХЭММИНГА
Линейные и систематические коды
В
систематических
кодах
формирование проверочных элементов
происходит по m информационным элементам кодовой комбинации. В
канал связи идет n элементная комбинация, состоящая из m
информационных и k проверочных разрядов.
В систематических кодах проверочные символы могут образовываться
путем различных линейных комбинаций информационных символов.
Декодирование систематических кодов основано на проверке линейных
соотношений между символами, стоящими на определенных проверочных
позициях. В случае двоичных кодов, этот процесс сводится к проверке на
четность.

28.

4
КОД ХЭММИНГА
Линейные и систематические коды
Линейными называются коды, в которых проверочные символы
представляют собой линейные комбинации информационных символов.
Для двоичных кодов в качестве линейной операции используют сложение
по модулю 2. Последовательность нулей и единиц, принадлежащих
данному коду, называется кодовым вектором.
СВОЙСТВО ЛИНЕЙНЫХ КОДОВ
Cумма или разность кодовых векторов линейного кода дает вектор,
принадлежащий данному коду.

29.

5
КОД ХЭММИНГА
Код Хэмминга
Ричард Уэсли Хэмминг (11.02.1915 – 7.01.1998)
Американский математик, работы которого в сфере
теории информации оказали существенное влияние на
компьютерные науки и телекоммуникации. Основной
вклад — т. н. код Хэмминга, а также расстояние
Хэмминга.
Хэмминг родился в Чикаго. Он получил степень бакалавра в Чикагском
университете в 1937 году. Затем он продолжил образование в Университете
Небраска и в 1939 году получил там степень магистра. В 1942 году он
защищает диссертацию в университете Иллинойс и становится доктором
философии. Некоторое время числится профессором в Университете
Луисвилль, где прерывает работу для участия в Манхэттенском проекте в
1945.
В рамках этого проекта Хэмминг занимается программированием одного из первых электронных
цифровых компьютеров для расчета решения физических уравнений. Цель программы состояла в том,
чтобы выяснить, не приведет ли взрыв атомной бомбы к возгоранию атмосферы. Ответ оказался
отрицательным, вследствие чего было принято решение об её использовании.
В период с 1946 по 1976 года Хэмминг работал в Bell Labs, где сотрудничал с Клодом Шенноном. 23 июля
1976 года он переехал в Монтеррей и возглавил там научные исследования в области вычислительной
техники в Высшем военно-морском училище. Скончался 7 января 1998 года в возрасте 82 лет.

30.

6
КОД ХЭММИНГА
Код Хэмминга. Краткое описание кода
Код Хэмминга исправляет одиночные ошибки. Он состоит из комбинации из m
информационных и k проверочных символов.
Избыточная часть кода строится таким образом, чтобы при декодировании можно
было установить не только наличие ошибки, но и ее расположение внутри
кодовой комбинации.
Достигается это путем многократной проверки принятой кодовой комбинации на
четность. При этом число проверок всегда равно числу контрольных разрядов k.
При каждой проверке охватывается часть информационных символов и один из
контрольных разрядов, в ходе проверке получают один проверочный символ.
Если результат проверки дает четное число, то проверочному символу
присваивается значение «0», в противном случае – «1».
В результате проверок получается k-разрядное двоичное число, указывающее
номер позиции искаженного символа. Если в результате проверки получена
комбинация из k нулей, значит ошибок в кодовой комбинации не обнаружено.

31.

7
КОД ХЭММИНГА
Код Хэмминга. Алгоритм кодирования
1. Расчет характеристик кода Хэмминга
n
2
2
1 n
m
Соотношения между параметрами кода m, k, n
n = m k
(7.13)

32.

8
КОД ХЭММИНГА
Код Хэмминга. Алгоритм кодирования
2. Определение структуры кодового вектора (позиции информационных и
контрольных разрядов)
i i = 0, 1, 2, 3, ...
2
Номера контрольных разрядов в этом случае будут
равны
1, 2, 4, 16, 32 …
3. Определение значений контрольных разрядов
Сумма единиц на проверочных позициях должна быть
четной
Если сумма четная – значение контрольного
коэффициента равно нулю, в противном случае –
единице

33.

9
КОД ХЭММИНГА
Код Хэмминга. Алгоритм кодирования
4. Определение проверочных позиций
5. Выявляют проверочные позиции
В результате первой проверки получается цифра младшего разряда
контрольного числа, в результате второй проверки – число второго
разряда, и т.д.
Значения информационных символов известны заранее, поэтому
контрольные символы необходимо выбирать таким образом, чтобы
сумма единиц была числом четным.
n = m k

34.

10
КОД ХЭММИНГА
Код Хэмминга. Пример
Закодировать кодом Хэмминга комбинацию 1 0 0 1 1
Число информационных разрядов m = 5
Число контрольных разрядов k = 4
Общее число разрядов n = m + k = 9
ПРОВЕРКА 1
k1 m1 m2 m4 m5 = 0
k1 1 0 1 1 = 0
k1 = 1

35.

11
КОД ХЭММИНГА
Код Хэмминга. Пример
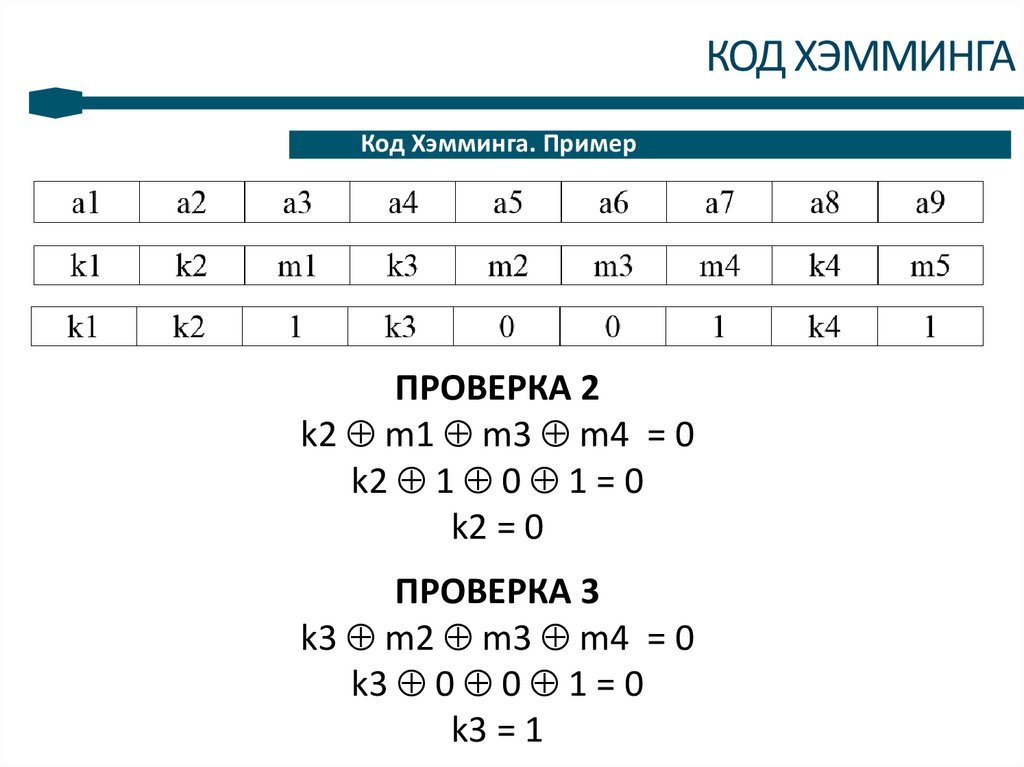
ПРОВЕРКА 2
k2 m1 m3 m4 = 0
k2 1 0 1 = 0
k2 = 0
ПРОВЕРКА 3
k3 m2 m3 m4 = 0
k3 0 0 1 = 0
k3 = 1

36.

12
КОД ХЭММИНГА
Код Хэмминга. Пример
ПРОВЕРКА 4
k4 m5 = 0
k4 1 = 0
k4 = 1
10011 101100111

37.

13
КОД ХЭММИНГА
Код Хэмминга. Пример
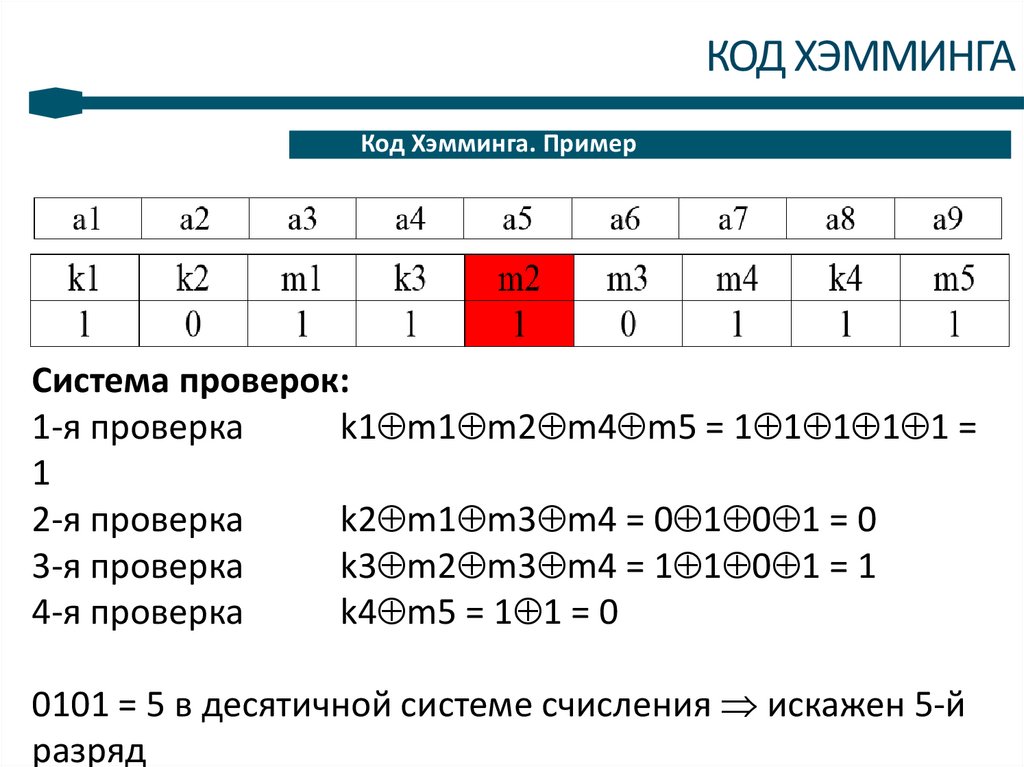
Система проверок:
1-я проверка
k1 m1 m2 m4 m5 = 1 1 1 1 1 =
1
2-я проверка
k2 m1 m3 m4 = 0 1 0 1 = 0
3-я проверка
k3 m2 m3 m4 = 1 1 0 1 = 1
4-я проверка
k4 m5 = 1 1 = 0
0101 = 5 в десятичной системе счисления искажен 5-й
разряд

38.

RОНТРОЛЬНЫЕ ВОПРОСЫ
Какие кодовые слова называются неперекрываемыми?
2. Запишите выражение для средней длины кодового слова?
3. Сформулируйте теорему существования.
4. Поясните принцип кодирования сообщений в коде Шеннона-Фано.
5. Поясните принцип кодирования сообщений в коде Хаффмана.
6. Сравните код Шеннона-Фано и код Хаффмана.
7. В чем преимущество кодирования групп сообщений?
8. Какие коды называются префиксными?
9. Перечислите недостатки систем эффективного кодирования.
10. Поясните принцип эффективного кодирования при неизвестной
статистике сообщений.
11. Основной принцип построения кода Хэмминга.
1.