Основні положення будівельної механіки. Кінематичний аналіз споруд

1.

Основні положення будівельної механіки.
Кінематичний аналіз споруд.
1.
2.
План:
Розрахункові схеми та основні елементи споруд.
Кінематичний аналіз споруд.

2.

Основні положення будівельної механіки
Будівельна механіка – це наука про методи
розрахунку споруд на міцність, жорсткість та
стійкість в умовах дії на них постійного та
тимчасового навантаження.

3.

Розрахункові схеми та основні елементи споруд.
У курсі будівельної механіки розглядається розрахунок
геометрично незмінних систем (споруд), тобто таких,
переміщення окремих точок яких можливі тільки в результаті
деформації систем. Нерухомість таких систем (їхня
геометрична незмінюваність) відносно землі забезпечується
опорними зв'язками (опорами). В опорах виникають реакції,
що разом із заданими навантаженнями встановлюють
урівноважену систему зовнішніх сил, що діють на споруду.

4.

Розрахункові схеми та основні елементи споруд.
Розрахункова схема – це спрощене, ідеалізоване зображення
дійсної споруди. Розрахунок споруд починають з вибору
розрахункової схеми. При цьому:
- ідеалізують опорні та вузлові з’єднання (або ідеальний
шарнір, або абсолютно жорсткий вузол);
- стержні споруди показують їх осями;
- перевіряють геометричну незмінність системи (переміщення
можливі тільки в результаті деформацій);
- виключають непрацюючі стержні, тобто ті, які не
навантажені і не потрібні для забезпечення стійкості споруди;
- ідеалізують навантаження на споруду.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

Основні положення будівельної механіки
До статично визначених систем належать
системи, зусилля в елементах яких розраховуються
за трьома рівнянями статики, які можна скласти
для плоскої системи сил.
Статично невизначуваними називають системи,
зусилля в яких неможливо обчислити за
допомогою одних лише рівнянь рівноваги.

16.

Розрахункові схеми та основні елементи споруд.
Розглянемо різні типи опор плоских систем:
Перший тип опори представлений на рис. 1. Він складається з двох
балансирів — верхнього 1 і нижнього 3, між якими прокладений
валик 2, що грає роль циліндричного шарніра. Завдяки цьому
валику верхній балансир може повертатися щодо нижнього. Крім
того, він може (разом з нижнім балансиром, що спирається на катки
Р
и 4) переміщатися по опорній площині, яка називається
опорною
с
1 подушкою 5.
1
Розглянута опора називається циліндрично-рухомою, або шарнірно
рухомою. Схематично її зображують у вигляді одного стержня з
двома ідеальними (без тертя) шарнірами на кінцях (рис. 2).
Рис. 1
Рис. 2

17.

Розрахункові схеми та основні елементи споруд.
Другий тип опори (рис. 3) відрізняється від першого тим, що нижній
балансир 3 закріплений і не може переміщуватися. Така опора має
одну ступінь вільності і називається циліндрично-нерухомою, або
шарнірно нерухомою.
Схематично опора другого типу зображується за допомогою двох
стержнів з ідеальними шарнірами на кінцях; верхній шарнір є
загальним для обох стержнів (рис. 4).
Рис. 4
Рис. 3

18.

Розрахункові схеми та основні елементи споруд.
Третім типом опори є защімлення (рис. 5), ступінь вільності якої
дорівнює нулю. Реакція такої опори визначається трьома
параметрами: величиною і напрямком сили, що проходить через
довільну точку, та моментом відносно цієї точки. Цю реакцію можна
представити як поєднання реактивного моменту в защімленні
(опорному перерізі) із реакцією шарнірно нерухомої опори.
Схематично опора третього типу може бути представлена трьома
стержнями (рис. 6); для того щоб защемлення можна було вважати
абсолютно твердим, відстань lо повинна бути дуже малою або брус
на ділянці довжиною lо треба розглядати як нескінченно твердий
Рис. 5
Рис. 6

19.

Кінематичний аналіз споруд
Змінність системи – її властивість змінювати свою геометричну
форму без деформації матеріалу елементів споруди. Змінні системи
не в змозі врівноважити зовнішні сили і під дією прикладених
навантажень приходять в рух, міняють свою форму.
Геометрично незмінна система – це така система, форма якої не
може мінятися без деформації матеріалу її елементів. Елементи
споруди, незмінність яких очевидна або доведена, називаються
дисками (стержень, земля). Рухоме з’єднання двох дисків, яке
обмежує взаємне їх переміщення, називається кінематичною в’яззю.

20.

Кінематичний аналіз споруд
Найпростішою геометрично незмінною шарнірною системою є
система
з трьох стержнів (дисків), з'єднаних шарнірами в
трикутник (рис. 7).
Рис. 7

21.

Кінематичний аналіз споруд
Стержнева система - це сукупність певного числа стержнів (два
основних розміри яких малі порівняно з третім), з'єднаних між
собою відповідним чином в'язями.
Ступінь вільності системи, складеної з дисків, з'єднаних між собою
шарнірами, визначається наступним чином. Якщо число дисків
позначити Д, а ступінь вільності кожного диска дорівнює трьом, то
розміщені на площині диски будуть мати ступінь вільності рівний
ЗД. Враховуючи, що кожен простий шарнір, число яких позначимо
Ш, зменшує ступінь вільності на два, а кожен опорний
стержень(опорна в'язь, число яких позначимо С0) - на одиницю, то
загальна ступінь вільності (W) стержневої системи визначиться за
формулою:
W=ЗД-2Ш-С0
(1)

22.

Кінематичний аналіз споруд
1. W > 0 – система немає достатньої кількості в’язей -геометрично
змінна, має рух;
2. W = 0 – система має достатнью кількость в’язей, необхідну для
забезпечення геометричної незмінності і нерухомості;
3. W < 0 – система незмінна, має зайву кількость в’язей, число яких
n = - W.
Для правильного застосування формули (1) потрібно розрізняти
шарніри прості – з’єднують два диски, і кратні - з’єднують більше
двох дисків. Число простих шарнірів Ш в кратному визначається
числом з’єднаних в ньому дисків (стержнів) Д зменшеним на
одиницю – Ш=2Д-1.

23.

Кінематичний аналіз споруд
Конструктивні елементи розрахункових схем
Розрахункова схема споруди складається з конструктивних
елементів, які можна поділити на два види: диски та з’єднувальні
пристрої.
Диски
Диском може бути названо будь-який елемент чи частину
розрахункової схеми, якщо заздалегідь задана або доведена її
геометрична незмінюваність. Диском можна назвати й усю систему,
якщо вона напевно геометрично незмінювана.
Особливо слід відзначити поняття простого диска, до якого
відносять геометрично незмінювану плоску однозв’язну фігуру,
тобто таку фігуру, всі границі якої можна “обійти” вздовж однієї
неперервної лінії, не перетинаючи тіло фігури.

24.

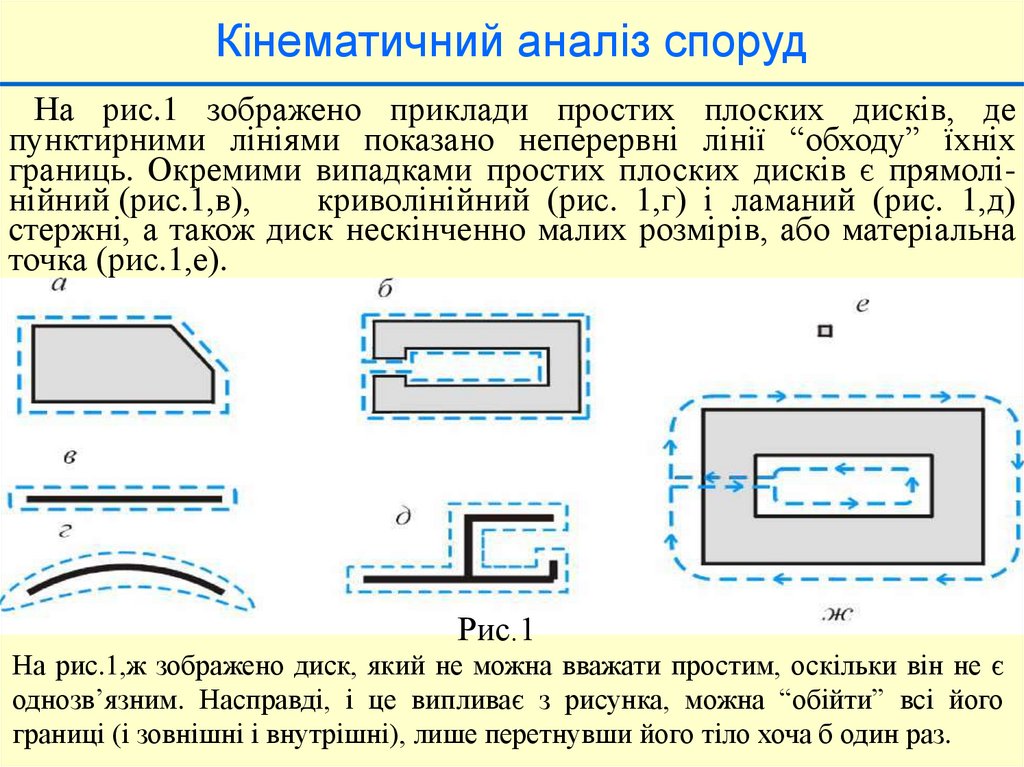
Кінематичний аналіз споруд
На рис.1 зображено приклади простих плоских дисків, де
пунктирними лініями показано неперервні лінії “обходу” їхніх
границь. Окремими випадками простих плоских дисків є прямолінійний (рис.1,в),
криволінійний (рис. 1,г) і ламаний (рис. 1,д)
стержні, а також диск нескінченно малих розмірів, або матеріальна
точка (рис.1,е).
Рис.1
На рис.1,ж зображено диск, який не можна вважати простим, оскільки він не є
однозв’язним. Насправді, і це випливає з рисунка, можна “обійти” всі його
границі (і зовнішні і внутрішні), лише перетнувши його тіло хоча б один раз.

25.

Кінематичний аналіз споруд
Простий плоский диск скінченних розмірів має три, а матеріальна
точка - два ступня вільності. Нагадаємо, що ступнем вільності диска
або системи дисків називається кількість незалежних геометричних
параметрів, що визначають положення диска (системи дисків)
стосовно будь-якої системи координат.
Кількість ступенів вільності диска або системи дисків
характеризується кількістю незалежних переміщень (лінійних чи
кутових), які можуть здійснювати елементи системи або вся система
стосовно системи координат. Можливість цих переміщень може
бути усунена за допомогою з’єднувальних пристроїв.

26.

Кінематичний аналіз споруд
З’єднувальні пристрої
З’єднувальний пристрій (з’єднання) - це елемент розрахункової
схеми споруди, який певним чином обмежує взаємне переміщення
дисків, що з’єднуються цим пристроєм, зменшуючи її ступінь
вільності.
Водночас кожен з’єднувальний пристрій має певні статичні
властивості, що характеризуються кількістю та видом реактивних
сил, що виникають у ньому.
У плоских розрахункових схемах застосовують такі основні типи
з’єднань: кінематичну в’язь, циліндричний шарнір, муфту,
припайку.

27.

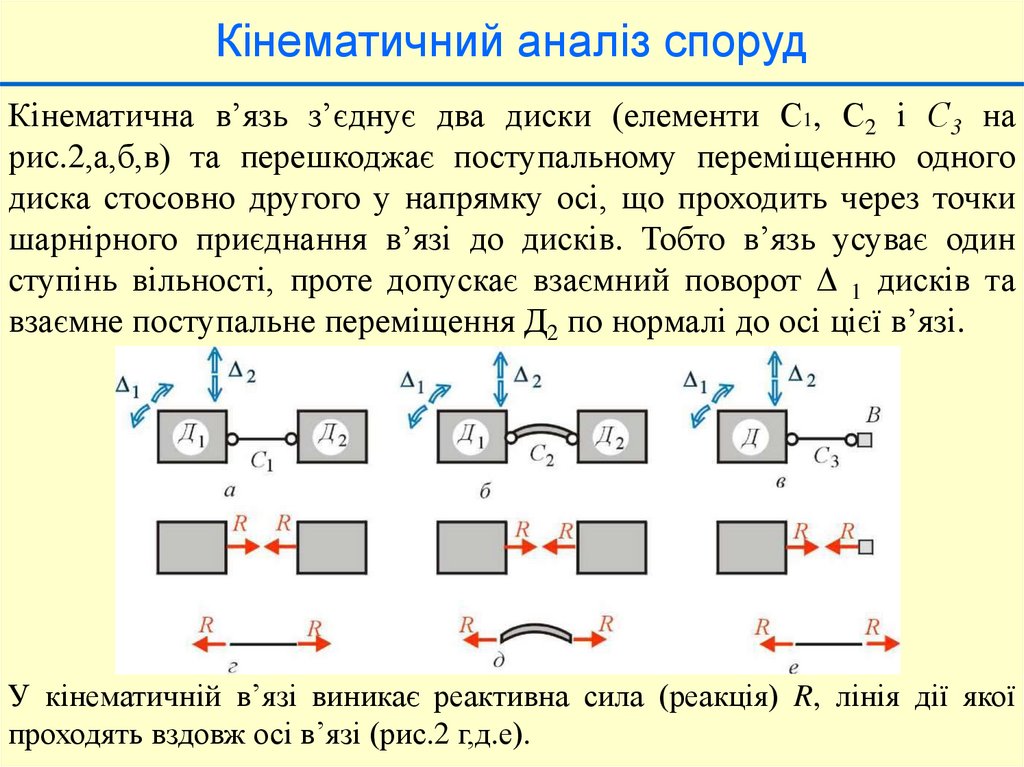
Кінематичний аналіз споруд
Кінематична в’язь з’єднує два диски (елементи С1, С2 і С3 на
рис.2,а,б,в) та перешкоджає поступальному переміщенню одного
диска стосовно другого у напрямку осі, що проходить через точки
шарнірного приєднання в’язі до дисків. Тобто в’язь усуває один
ступінь вільності, проте допускає взаємний поворот Δ 1 дисків та
взаємне поступальне переміщення Д2 по нормалі до осі цієї в’язі.
У кінематичній в’язі виникає реактивна сила (реакція) R, лінія дії якої
проходять вздовж осі в’язі (рис.2 г,д.е).

28.

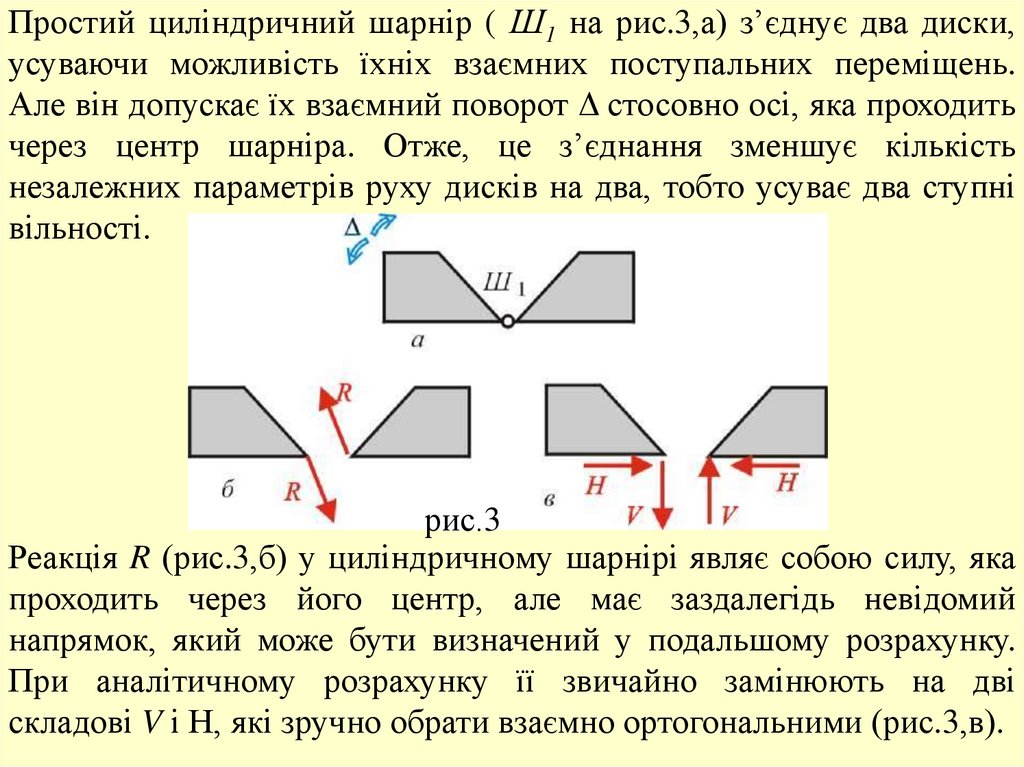
Простий циліндричний шарнір ( Ш1 на рис.3,а) з’єднує два диски,
усуваючи можливість їхніх взаємних поступальних переміщень.
Але він допускає їх взаємний поворот Δ стосовно осі, яка проходить
через центр шарніра. Отже, це з’єднання зменшує кількість
незалежних параметрів руху дисків на два, тобто усуває два ступні
вільності.
рис.3
Реакція R (рис.3,б) у циліндричному шарнірі являє собою силу, яка
проходить через його центр, але має заздалегідь невідомий
напрямок, який може бути визначений у подальшому розрахунку.
При аналітичному розрахунку її звичайно замінюють на дві
складові V і Н, які зручно обрати взаємно ортогональними (рис.3,в).

29.

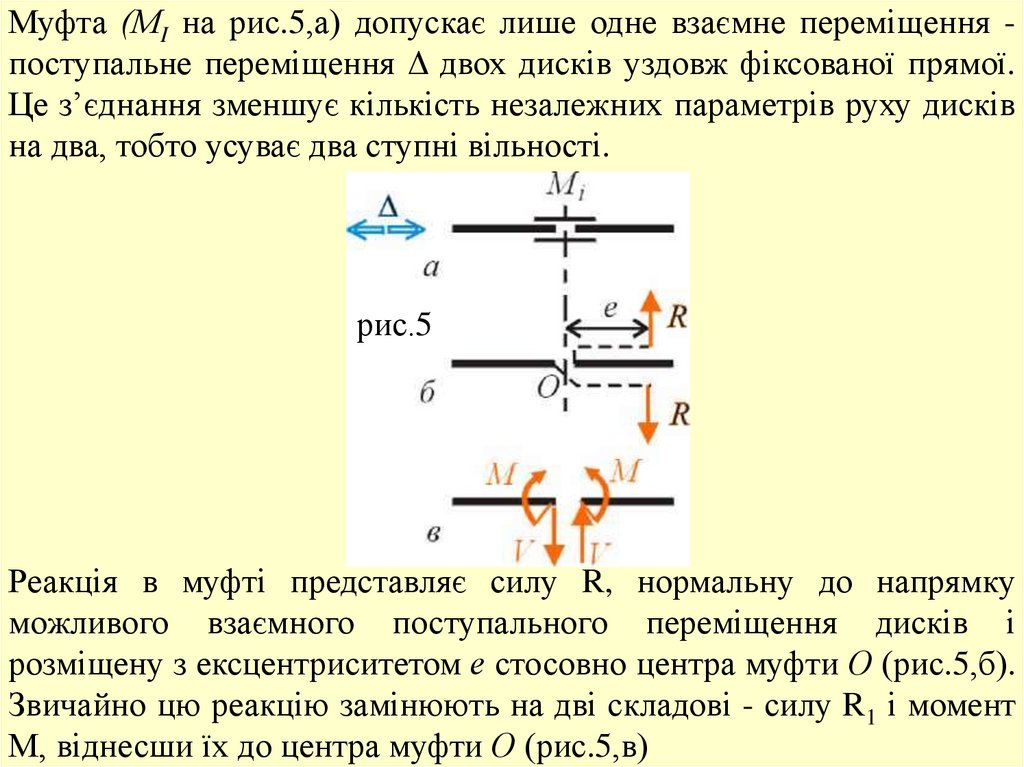
Муфта (МI на рис.5,а) допускає лише одне взаємне переміщення поступальне переміщення Δ двох дисків уздовж фіксованої прямої.
Це з’єднання зменшує кількість незалежних параметрів руху дисків
на два, тобто усуває два ступні вільності.
рис.5
Реакція в муфті представляє силу R, нормальну до напрямку
можливого взаємного поступального переміщення дисків і
розміщену з ексцентриситетом е стосовно центра муфти О (рис.5,б).
Звичайно цю реакцію замінюють на дві складові - силу R1 і момент
М, віднесши їх до центра муфти О (рис.5,в)

30.

Проста припайка (ПІ на рис.6,а) повністю виключає взаємні
поступальні та кутові переміщення двох дисків, які нею
з’єднуються. Це з’єднання зменшує кількість незалежних
параметрів руху дисків на три, тобто усуває три ступні вільності
рис.6
Реакція в припайці - це сила R, лінія дії та ексцентриситет е якої
стосовно центра припайки О заздалегідь невідомі (рис.2.8,б). Цю
реакцію зручно замінювати на три складові, віднесені до центра
припайки О: двох взаємно перпендикулярних сил Vі Н, а також
моменту М (рис.2.8,в).

31.

Зв’язок між простими з’єднувальними пристроями
Між різними простими з’єднаннями існує взаємний зв’язок, який,
якщо це необхідно або зручно для проведення аналізу, надає змогу
замінювати одні з’єднання іншими, не змінюючи при цьому їх
кінематичні та статичні властивості.
Так, простий циліндричний шарнір Ш1,2 (рис.7,а), що усуває два
взаємних поступальних переміщення дисків Д1 і Д2, можна
замінити на дві кінематичні в’язі С1 і С2 (рис.7,б), що перетинаються в центрі шарніра, що замінюється.

32.

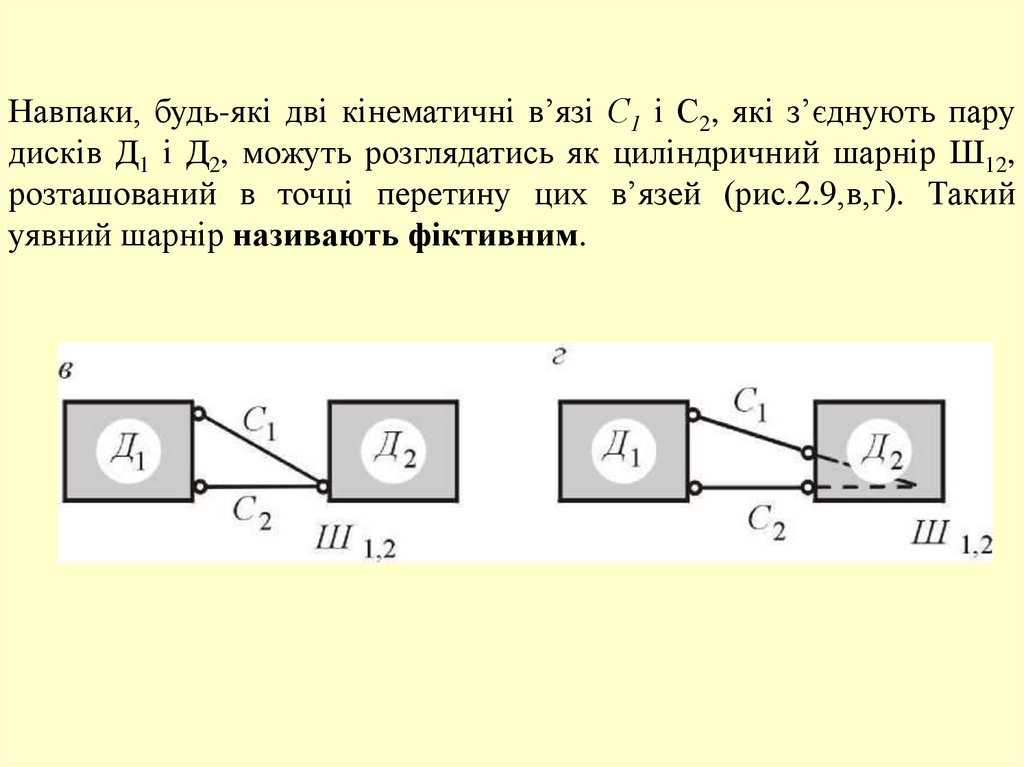
Навпаки, будь-які дві кінематичні в’язі С1 і С2, які з’єднують пару
дисків Д1 і Д2, можуть розглядатись як циліндричний шарнір Ш12,
розташований в точці перетину цих в’язей (рис.2.9,в,г). Такий
уявний шарнір називають фіктивним.

33.

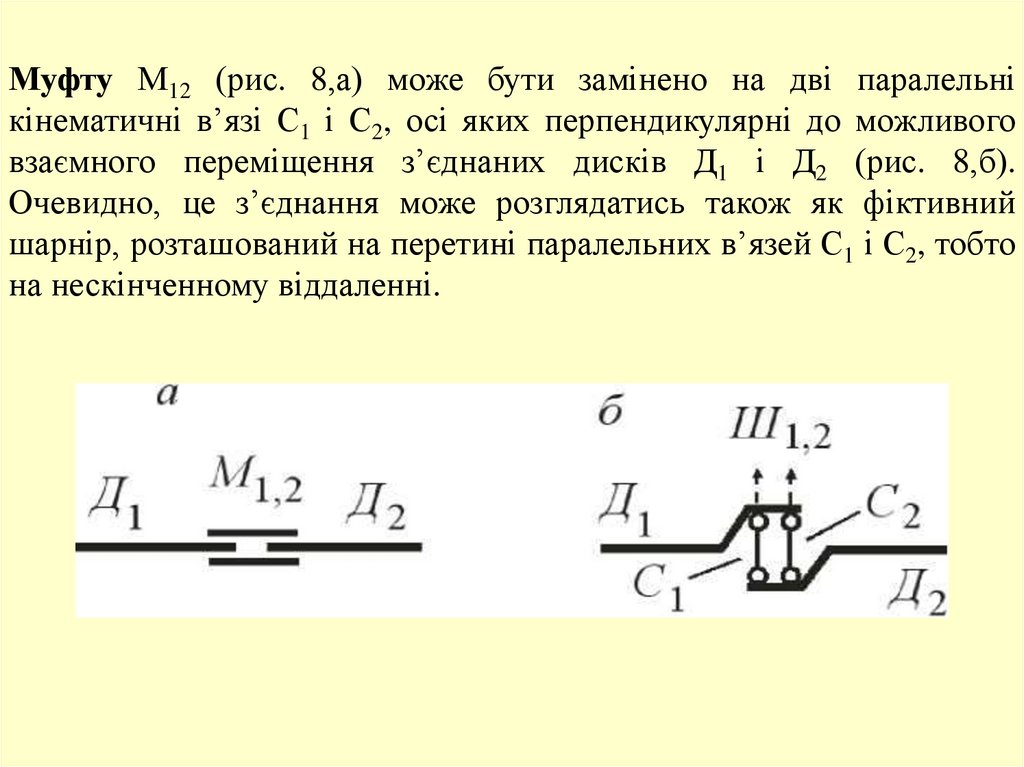
Муфту М12 (рис. 8,а) може бути замінено на дві паралельні
кінематичні в’язі С1 і С2, осі яких перпендикулярні до можливого
взаємного переміщення з’єднаних дисків Д1 і Д2 (рис. 8,б).
Очевидно, це з’єднання може розглядатись також як фіктивний
шарнір, розташований на перетині паралельних в’язей С1 і С2, тобто
на нескінченному віддаленні.

34.

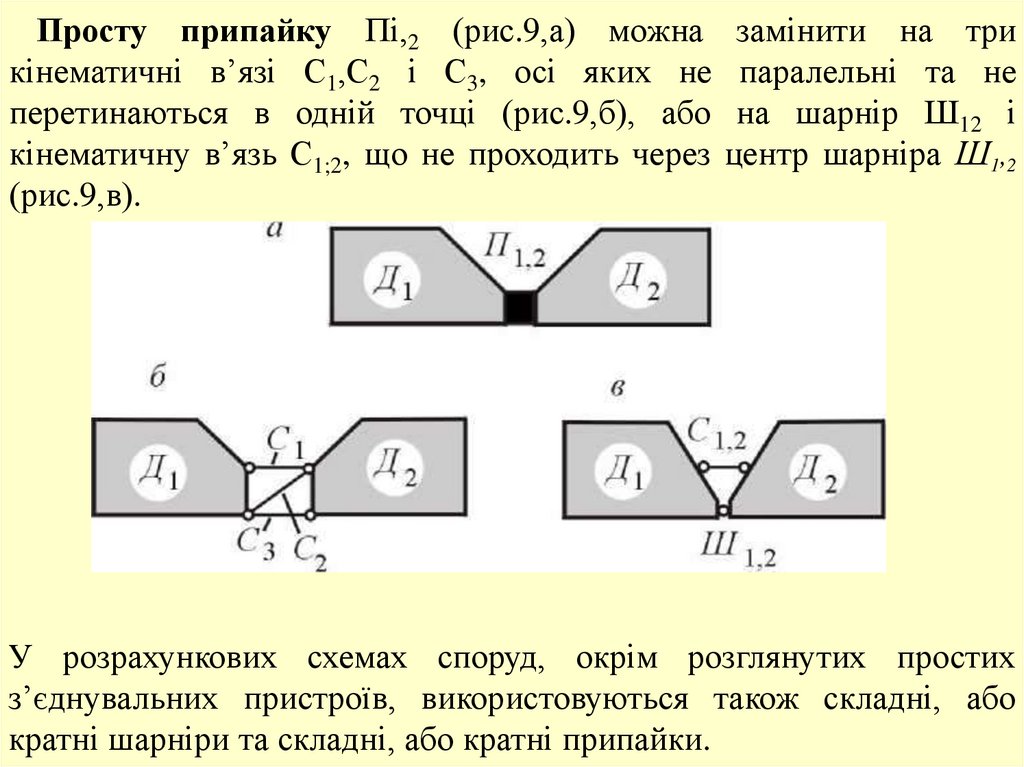
Просту припайку Пі,2 (рис.9,а) можна замінити на три
кінематичні в’язі С1,С2 і С3, осі яких не паралельні та не
перетинаються в одній точці (рис.9,б), або на шарнір Ш12 і
кінематичну в’язь С1;2, що не проходить через центр шарніра Ш1,2
(рис.9,в).
У розрахункових схемах споруд, окрім розглянутих простих
з’єднувальних пристроїв, використовуються також складні, або
кратні шарніри та складні, або кратні припайки.

35.

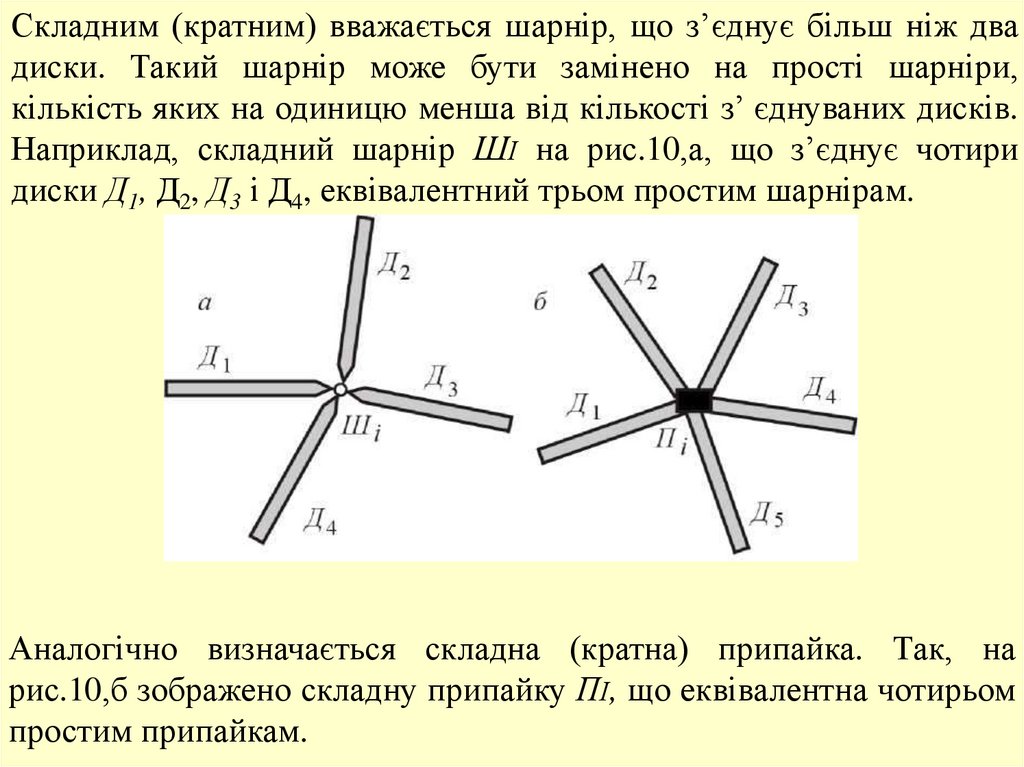
Складним (кратним) вважається шарнір, що з’єднує більш ніж два
диски. Такий шарнір може бути замінено на прості шарніри,
кількість яких на одиницю менша від кількості з’ єднуваних дисків.
Наприклад, складний шарнір ШІ на рис.10,а, що з’єднує чотири
диски Д1, Д2, Д3 і Д4, еквівалентний трьом простим шарнірам.
Аналогічно визначається складна (кратна) припайка. Так, на
рис.10,б зображено складну припайку ПІ, що еквівалентна чотирьом
простим припайкам.

36.

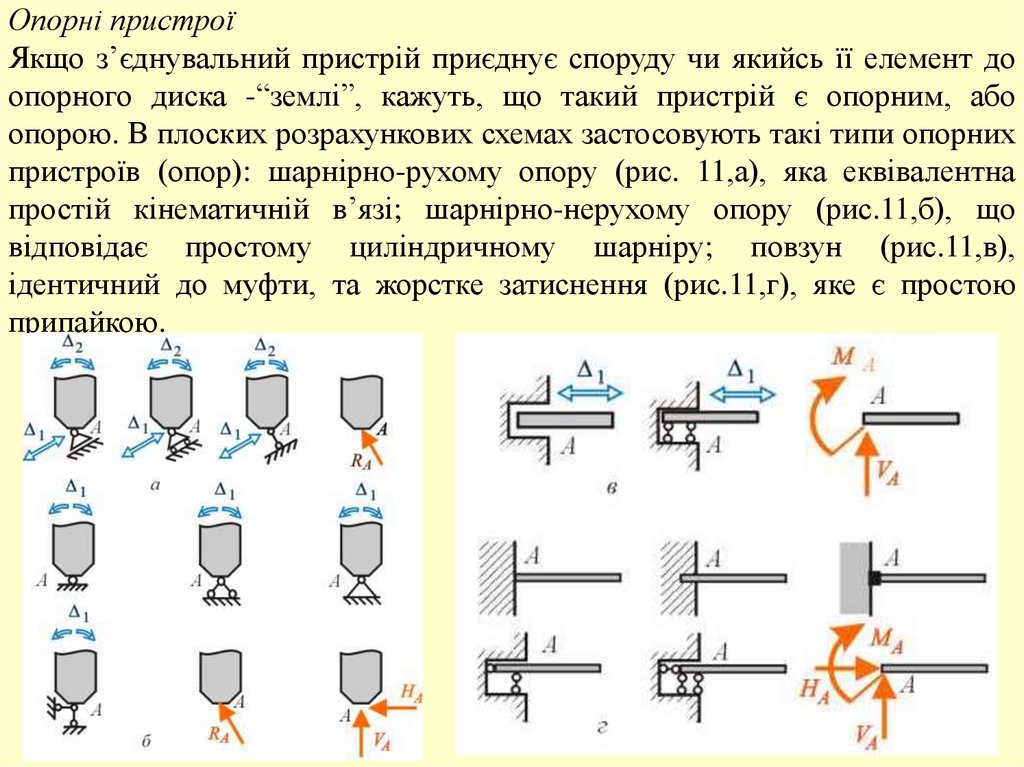
Опорні пристрої
Якщо з’єднувальний пристрій приєднує споруду чи якийсь її елемент до
опорного диска -“землі”, кажуть, що такий пристрій є опорним, або
опорою. В плоских розрахункових схемах застосовують такі типи опорних
пристроїв (опор): шарнірно-рухому опору (рис. 11,а), яка еквівалентна
простій кінематичній в’язі; шарнірно-нерухому опору (рис.11,б), що
відповідає простому циліндричному шарніру; повзун (рис.11,в),
ідентичний до муфти, та жорстке затиснення (рис.11,г), яке є простою
припайкою.

37.

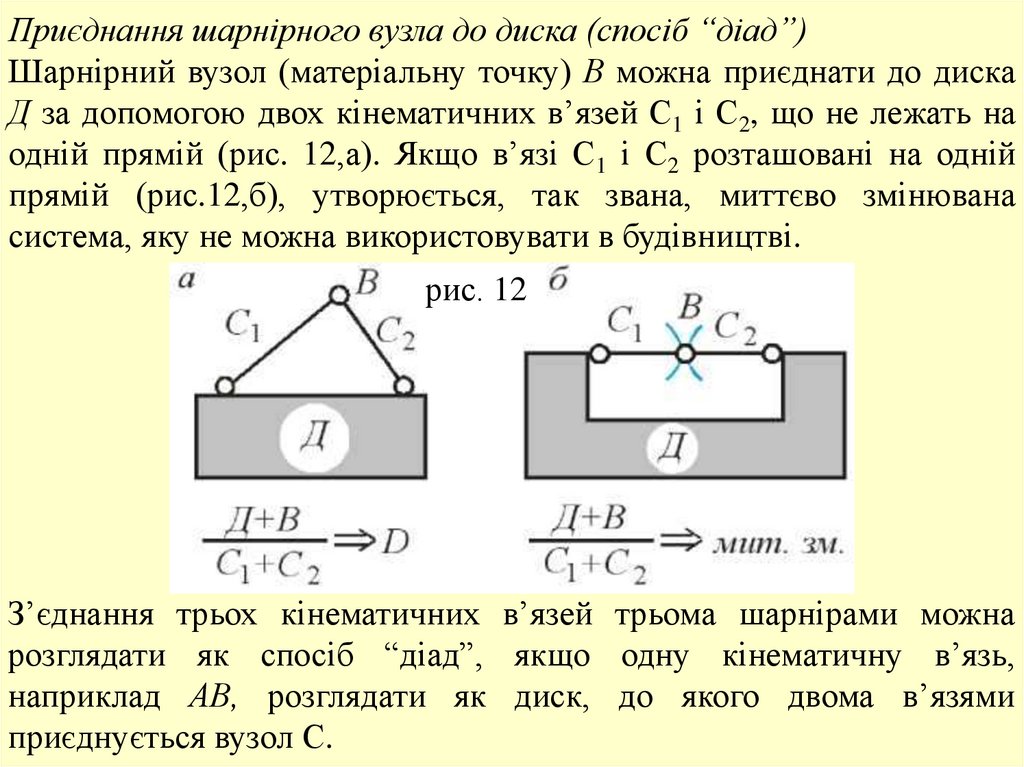
Приєднання шарнірного вузла до диска (спосіб “діад”)
Шарнірний вузол (матеріальну точку) В можна приєднати до диска
Д за допомогою двох кінематичних в’язей С1 і С2, що не лежать на
одній прямій (рис. 12,а). Якщо в’язі С1 і С2 розташовані на одній
прямій (рис.12,б), утворюється, так звана, миттєво змінювана
система, яку не можна використовувати в будівництві.
рис. 12
З’єднання трьох кінематичних в’язей трьома шарнірами можна
розглядати як спосіб “діад”, якщо одну кінематичну в’язь,
наприклад АВ, розглядати як диск, до якого двома в’язями
приєднується вузол С.

38.

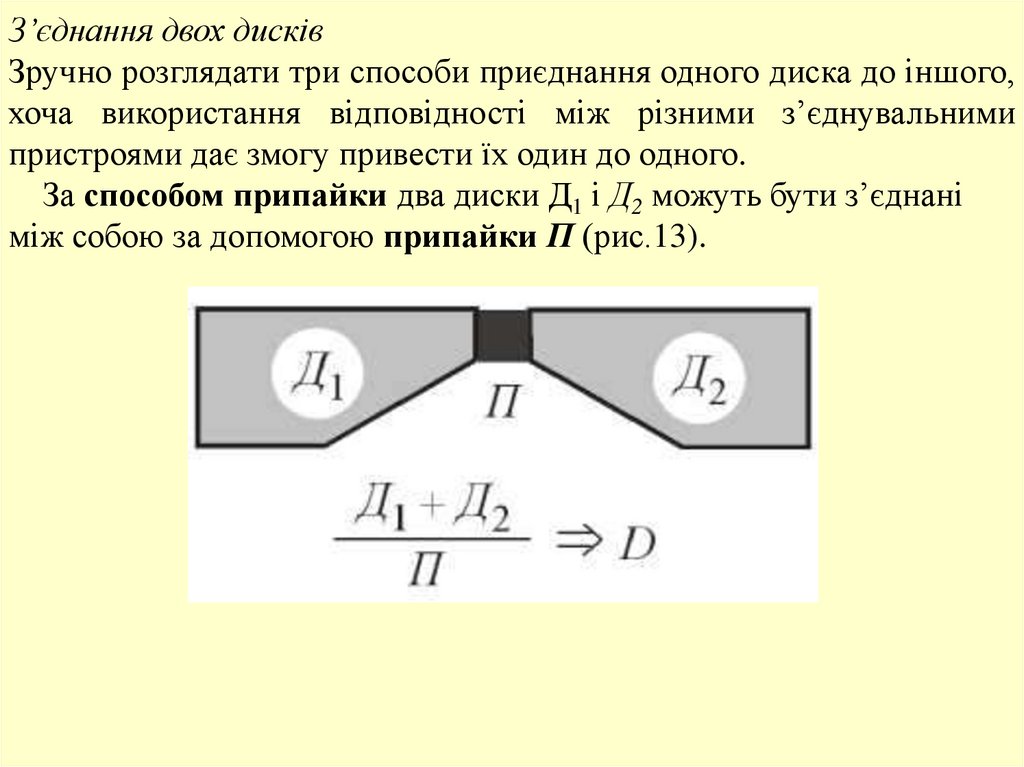
З’єднання двох дисків
Зручно розглядати три способи приєднання одного диска до іншого,
хоча використання відповідності між різними з’єднувальними
пристроями дає змогу привести їх один до одного.
За способом припайки два диски Д1 і Д2 можуть бути з’єднані
між собою за допомогою припайки П (рис.13).

39.

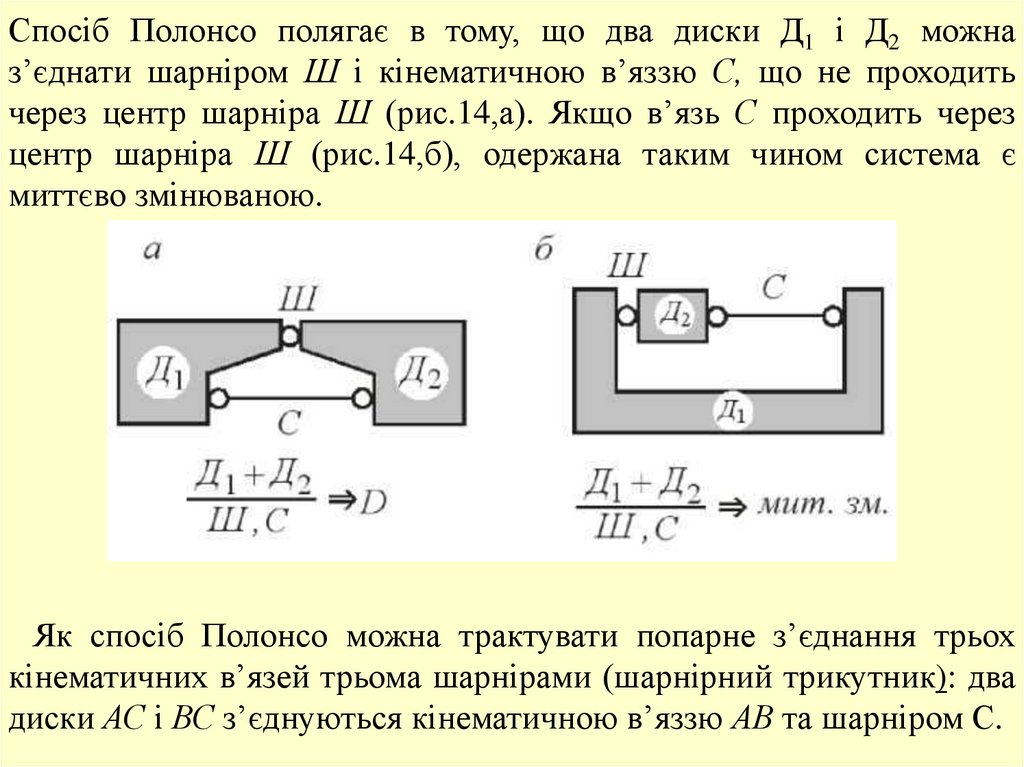
Спосіб Полонсо полягає в тому, що два диски Д1 і Д2 можна
з’єднати шарніром Ш і кінематичною в’яззю С, що не проходить
через центр шарніра Ш (рис.14,а). Якщо в’язь С проходить через
центр шарніра Ш (рис.14,б), одержана таким чином система є
миттєво змінюваною.
Як спосіб Полонсо можна трактувати попарне з’єднання трьох
кінематичних в’язей трьома шарнірами (шарнірний трикутник): два
диски АС і ВС з’єднуються кінематичною в’яззю АВ та шарніром С.

40.

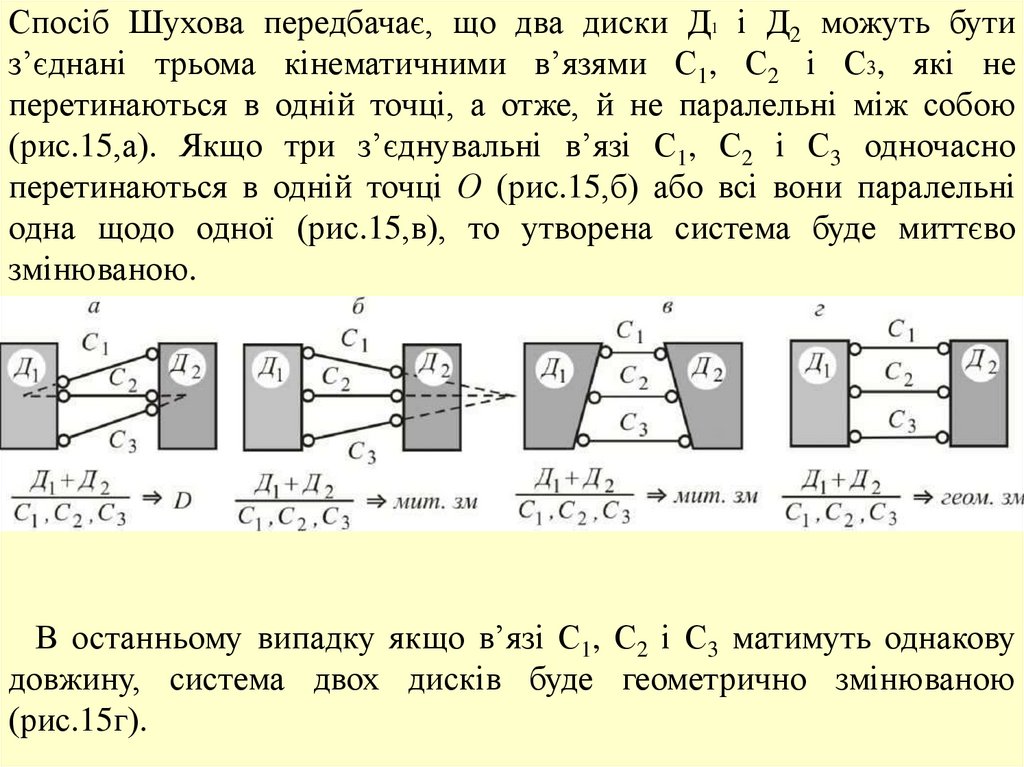
Спосіб Шухова передбачає, що два диски Д1 і Д2 можуть бути
з’єднані трьома кінематичними в’язями С1, С2 і С3, які не
перетинаються в одній точці, а отже, й не паралельні між собою
(рис.15,а). Якщо три з’єднувальні в’язі С1, С2 і С3 одночасно
перетинаються в одній точці О (рис.15,б) або всі вони паралельні
одна щодо одної (рис.15,в), то утворена система буде миттєво
змінюваною.
В останньому випадку якщо в’язі С1, С2 і С3 матимуть однакову
довжину, система двох дисків буде геометрично змінюваною
(рис.15г).

41.

З’єднання трьох дисків (спосіб шарнірного трикутника)
Три диски Д1, Д2 і Д3 можна з’єднати за допомогою трьох шарнірів
(реальних або фіктивних) Ш1,2, Ш1,3 і Ш2,3, які не лежать на одній
прямій (рис.16,а). Причому фіктивні шарніри (але не більш, ніж два з
них) можуть бути і нескінченно віддаленими.
1.
Так, усі три шарніри Ш12, Ш13 і Ш23, які з’єднують три диски Д1, Д2 і Д3 на
рис.16а, є дійсними. На рис.16,б диски Д1 і Д3 з’єднані дійсним шарніром
Ш13, диски Д1 і Д2 — фіктивним шарніром Ш12, розташованим у точці
перетину в’язей С1 і С2, що його утворили, а диски Д2 і Д3 - фіктивним
шарніром Ш23, утвореним в’язями С3 і С4 і розташованим на їх перетині.

42.

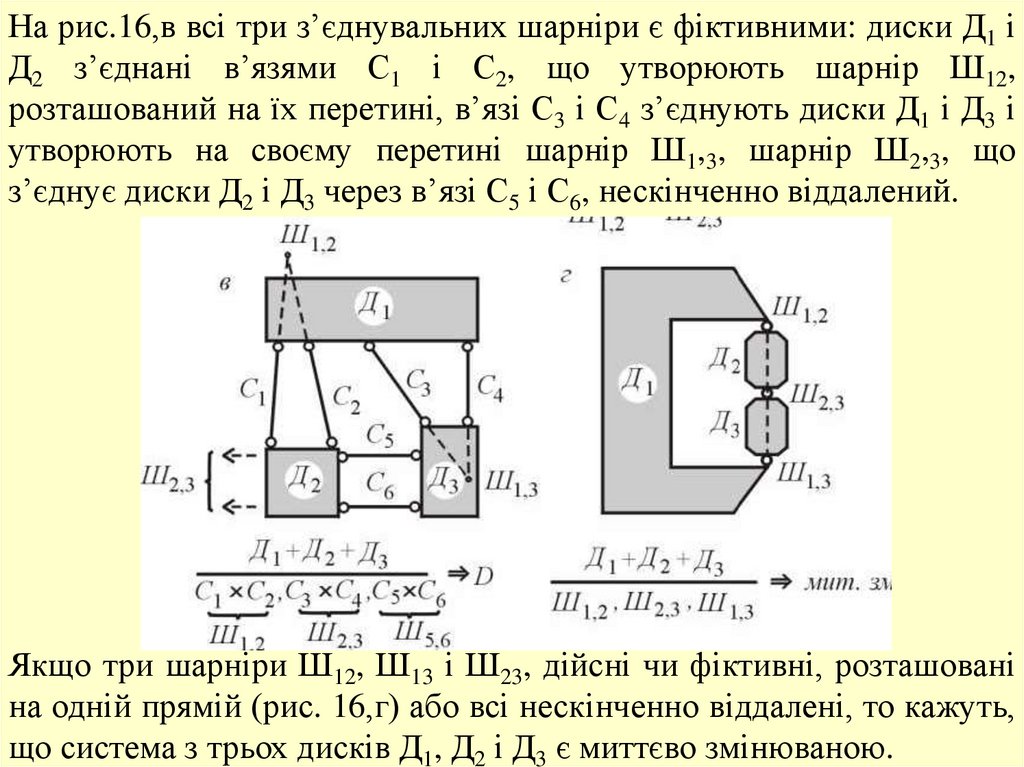
На рис.16,в всі три з’єднувальних шарніри є фіктивними: диски Д1 і
Д2 з’єднані в’язями С1 і С2, що утворюють шарнір Ш12,
розташований на їх перетині, в’язі С3 і С4 з’єднують диски Д1 і Д3 і
утворюють на своєму перетині шарнір Ш1,3, шарнір Ш2,3, що
з’єднує диски Д2 і Д3 через в’язі С5 і С6, нескінченно віддалений.
Якщо три шарніри Ш12, Ш13 і Ш23, дійсні чи фіктивні, розташовані
на одній прямій (рис. 16,г) або всі нескінченно віддалені, то кажуть,
що система з трьох дисків Д1, Д2 і Д3 є миттєво змінюваною.

43.

Кінематичний аналіз споруд
Миттєво змінювана система – це система з’єднання дисків
(стержнів), які допускають без деформації матеріалу безкінечно
малі переміщення дисків (стержнів) в перший момент прикладення
навантаження, після чого система стає незмінною.
Способи побудови споруд:
Системи, отримані із шарнірного трикутника шляхом послідовного
приєднання вузлів, причому кожного двома стержнями, що не
лежать на одній прямій, геометрично незмінні, тобто геометрична
структура їх незмінна. Такі системи (або ферми) називають
найпростішими, на відміну від складних, які утворюються,
зазвичай, в результаті видозміни найпростіших.
Два диски утворять геометрично незмінну систему, якщо вони
зв'язані між собою за допомогою трьох стержнів, осі яких не
перетинаються в одній точці і не паралельні між собою (спосіб
Шухова).

44.

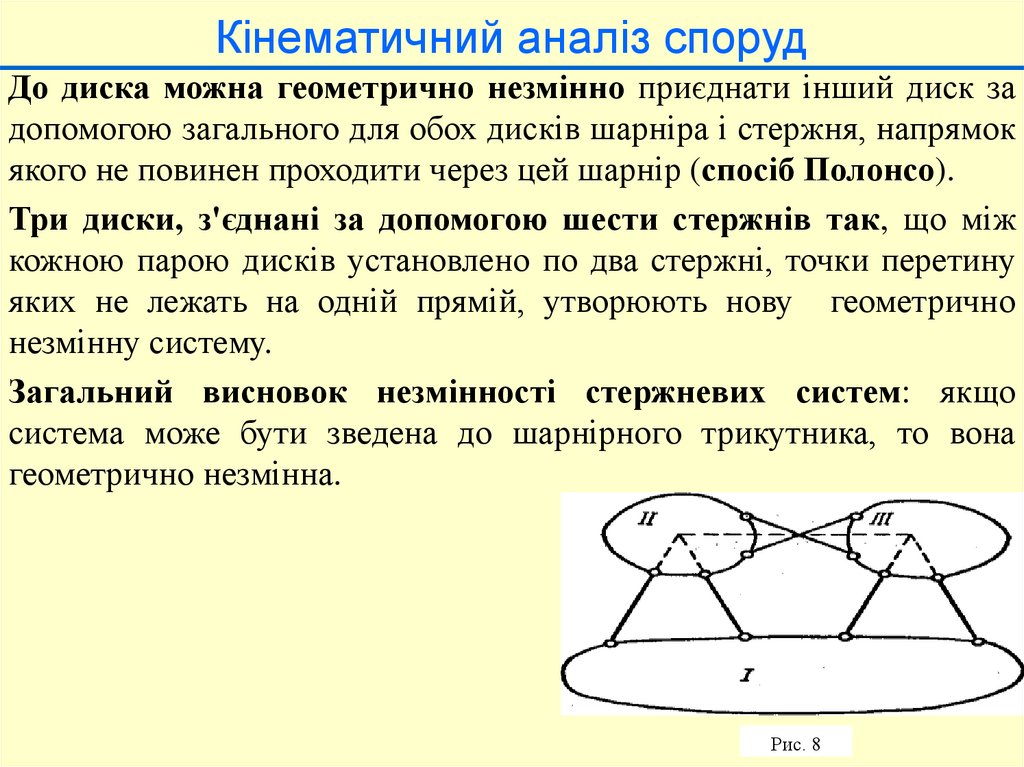
Кінематичний аналіз споруд
До диска можна геометрично незмінно приєднати інший диск за
допомогою загального для обох дисків шарніра і стержня, напрямок
якого не повинен проходити через цей шарнір (спосіб Полонсо).
Три диски, з'єднані за допомогою шести стержнів так, що між
кожною парою дисків установлено по два стержні, точки перетину
яких не лежать на одній прямій, утворюють нову геометрично
незмінну систему.
Загальний висновок незмінності стержневих систем: якщо
система може бути зведена до шарнірного трикутника, то вона
геометрично незмінна.
Рис. 8

45.

Кінематичний аналіз споруд
Порядок проведення кінематичного аналізу споруд:
- вибір розрахункової схеми споруди;
-визначення числа ступенів вільності системи;
- виділення незмінних частин споруди – дисків;
- проведення аналізу з’єднань дисків між собою.

46.

Кінематичний аналіз споруд
Кількісний етап кінематичного аналізу
При виконання першого етапу кінематичного аналізу
визначається кількісна характеристика її змінюваності – ступінь
геометричної змінюваності. Для цього необхідно підсумувати
ступені вільності окремих складових елементів системи та відняти
від цього числа суму ступенів вільності, які усувають всі з’єднання.
Виходячи з викладених вище кінематичних властивостей
елементів розрахункових схем, можна записати модифікацію
формули Чебишова для визначення ступеня геометричної
змінюваності Г системи:
(2)
Г = 3Д + 2В - 3П - 2Ш - С - 3,
де: Д - кількість простих дисків, включаючи опорний диск “землю”, якщо
система прикріплена до неї; В - кількість матеріальних точок, тобто вузлів,
в яких з’єднуються лише кінематичні в’язі; П - кількість простих
припайок; Ш - кількість простих шарнірів; С - кількість кінематичних
в’язей; 3 (три) - число ступенів вільності всієї плоскої розрахункової
схеми як одного геометрично незмінюваного складеного диска в своїй
площині.

47.

Кінематичний аналіз споруд
Г > 0, то розрахункова схема споруди є геометрично змінюваною.
Г = 0, то розрахункова схема споруди є геометрично не змінюваною.
Г < 0, то розрахункова схема споруди є геометрично не змінюваною.
Остаточно про геометричну незмінюваність розрахункової схеми
при Г ≤ 0 можна стверджувати лише після виконання її якісного
(структурного) аналізу.
Якісний (структурний) етап кінематичного аналізу
Якісний (структурний) аналіз розрахункової схеми полягає у
визначенні послідовності та способів утворення системи зі
складових елементів. З’єднання всієї системи або її фрагментів
повинно виконуватись відповідно до способів правильного
поєднання елементів у геометрично незмінювані системи – складені
диски.

48.

Кінематичний аналіз споруд
Далі розглянуто основні способи утворення найпростіших
геометрично незмінюваних плоских систем при використанні
мінімальної кількості з’єднувальних пристроїв. При їх поданні
поруч з відповідною схемою поєднання простих дисків у складений
використовуються умовні “формули”, що мають вигляд дробу, в
чисельнику якого міститься перелік з’єднаних елементів, а у
знаменнику - перелік з’єднувальних пристроїв. Після знака “ “
записується назва укрупненого складеного диска, який позначається
великою латинською літерою D з нижнім індексом. Якщо з’єднання
виконано за допомогою фіктивного шарніра, та в знаменнику
подається найменування двох в’язей, які утворюють цей шарнір, із
символом “×“ між ними.

49.

Кінематичний аналіз споруд
Остаточний висновок про геометричну незмінюваність,
геометричну або миттєву змінюваність розрахункової схеми
споруди. Якщо доведено правильне приєднання всіх елементів
системи, вся розрахункова схема може вважатись геометрично
незмінюваною. Якщо виявляється, що для з’єднання одних
елементів використані зайві пристрої, а для інших їх бракує, всю
розрахункову схему вважають геометрично змінюваною. Якщо ж
хоча б одне з’єднання виконується як у винятку з якогось способу,
що відповідає миттєвій змінюваності фрагмента, схема є миттєво
змінюваною.

50.

Кінематичний аналіз споруд
Визначення сил взаємодії дисків. Найбільш поширеним
способом визначення сил взаємодії дисків є використання методу
перерізів, який полягає в тому, що від розрахункової моделі споруди
уявним наскрізним перерізом відокремлюється якийсь його
фрагмент (диск або група дисків). Вплив „розрізаних” перерізом
з’єднань замінюються силами - реакціями цих з’єднань. Таким
чином, на відокремлений фрагмент діє система зовнішніх сил, яка
складається з активного навантаження та реакціями в’язей.

51.

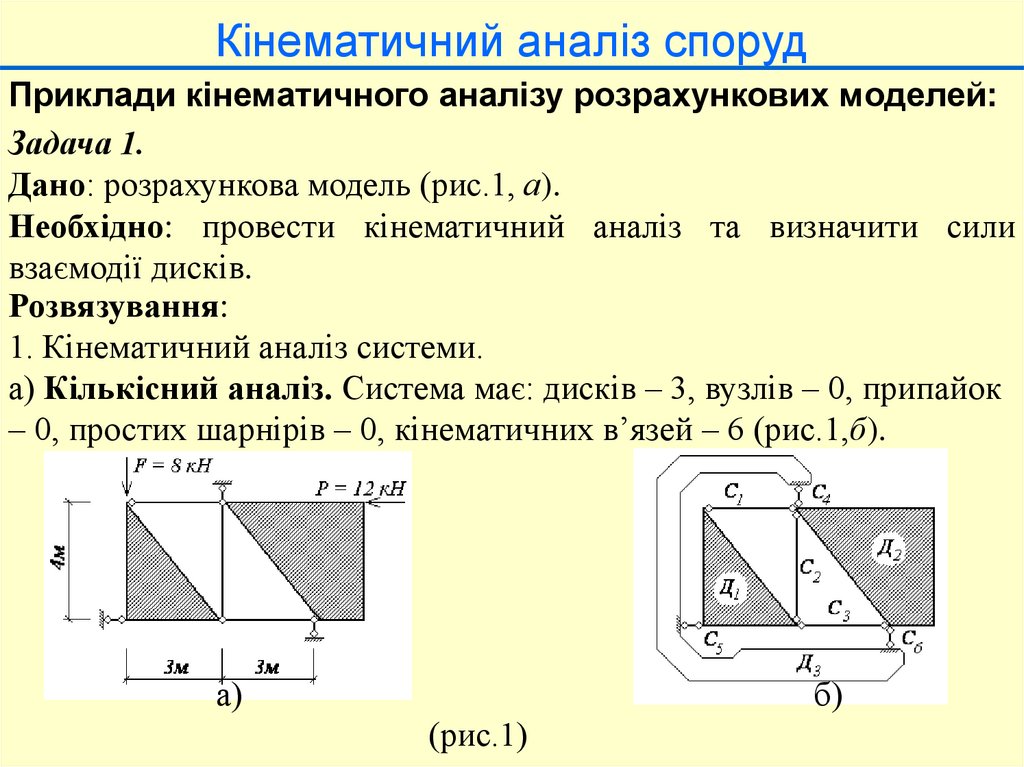
Кінематичний аналіз споруд
Приклади кінематичного аналізу розрахункових моделей:
Задача 1.
Дано: розрахункова модель (рис.1, а).
Необхідно: провести кінематичний аналіз та визначити сили
взаємодії дисків.
Розвязування:
1. Кінематичний аналіз системи.
а) Кількісний аналіз. Система має: дисків – 3, вузлів – 0, припайок
– 0, простих шарнірів – 0, кінематичних в’язей – 6 (рис.1,б).
а)
б)
(рис.1)

52.

Кінематичний аналіз споруд
За формулою Чебишова (2):
Г = 3 ∙ Д + 2В - 3П - 2Ш -С - 3 = 3 ∙ 3 + 2 ∙ 0 - 3 ∙ 0 - 2 ∙ 0 - 6 - 3 = = 9 9=0,
Висновок: система статично визначувана і може бути
геометрично незмінюваною.
б) Якісний аналіз.
Розрахункова схема будується в два етапи:
На першому етапі поєднуються диски Д1 та Д2 методом Шухова
Д Д
1
2 D
I
С ,С ,С
1 2 3
Другий етап створення розрахункової моделі (рис. 2,б) також
використовує метод Шухова
D Д
I
3 D
IІ
С ,С ,С
4 5 6

53.

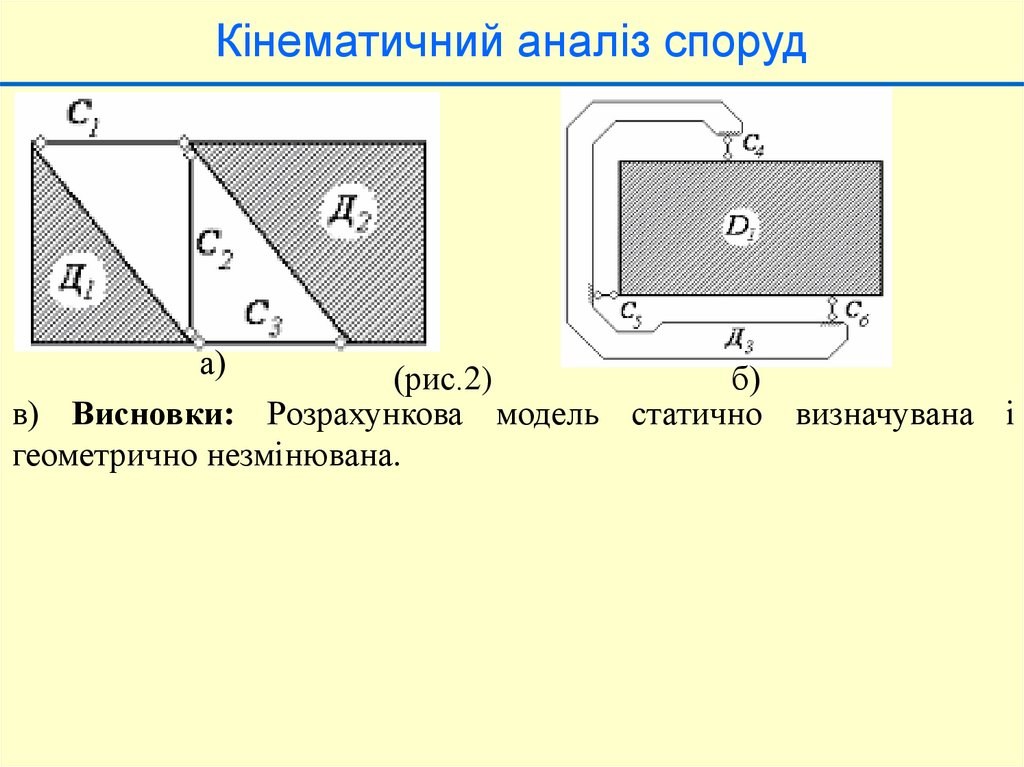
Кінематичний аналіз споруд
а)
(рис.2)
б)
в) Висновки: Розрахункова модель статично визначувана і
геометрично незмінювана.

54.

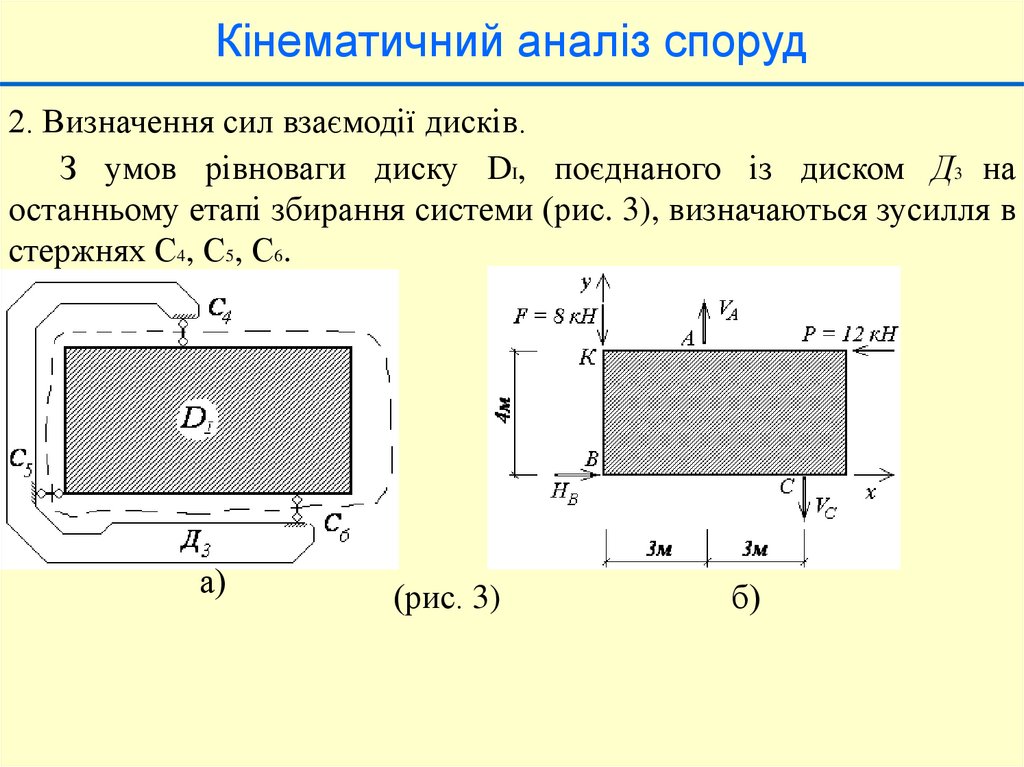
Кінематичний аналіз споруд
2. Визначення сил взаємодії дисків.
З умов рівноваги диску DI, поєднаного із диском Д3 на
останньому етапі збирання системи (рис. 3), визначаються зусилля в
стержнях С4, С5, С6.
а)
(рис. 3)
б)

55.

Кінематичний аналіз споруд
Перевірка рівноваги у в’язях:

56.

Кінематичний аналіз споруд
Визначення реакцій у в’язях, використаних на першому етапі
збирання конструкції:
(рис. 4)

57.

Кінематичний аналіз споруд
Перевірка рівноваги у в’язях:

58.

Кінематичний аналіз споруд
Дано: розрахункова модель (рис. 5).
Необхідно: провести кінематичний аналіз споруди.
Розвязування:
1. Кінематичний аналіз системи.
а) Кількісний аналіз. Система має: дисків –
3, вузлів – 0, припайок – 0, простих шарнірів
– 1, кінематичних в’язей (стержнів) – 4
(рис.6).
За формулою Чебишова (2):
Г = 3 ∙ Д + 2В - 3П - 2Ш -С - 3 = 3 ∙ 3 + 2 ∙
∙0-3∙0-2∙1-4-3= 9-9=0,
система статично
незмінюваною.
визначувана
і
може
рис. 5
бути геометрично

59.

Кінематичний аналіз споруд
б) Якісний аналіз.
Розрахункова схема будується в один
етап: диски Д1, Д2 та Д3 методом шарнірного
трикутника за допомогою шарніра Ш1-2 та
двох фіктивних шарнірів, утворених
парами стержнів С1, С2 та С3, С4. Однак
утворена система не може бути диском, т.я.
три шарніри лежать на одній прямій – отже
система миттєво визначувана (рис.6):
Д Д Д
1
2
3
D
Ш
,С С ,С С
1 2
1
2
3
4
ШФ ШФ
1 2
3 4
рис. 6
в) Висновок. Розрахункова модель є миттєво змінюваною.

60.

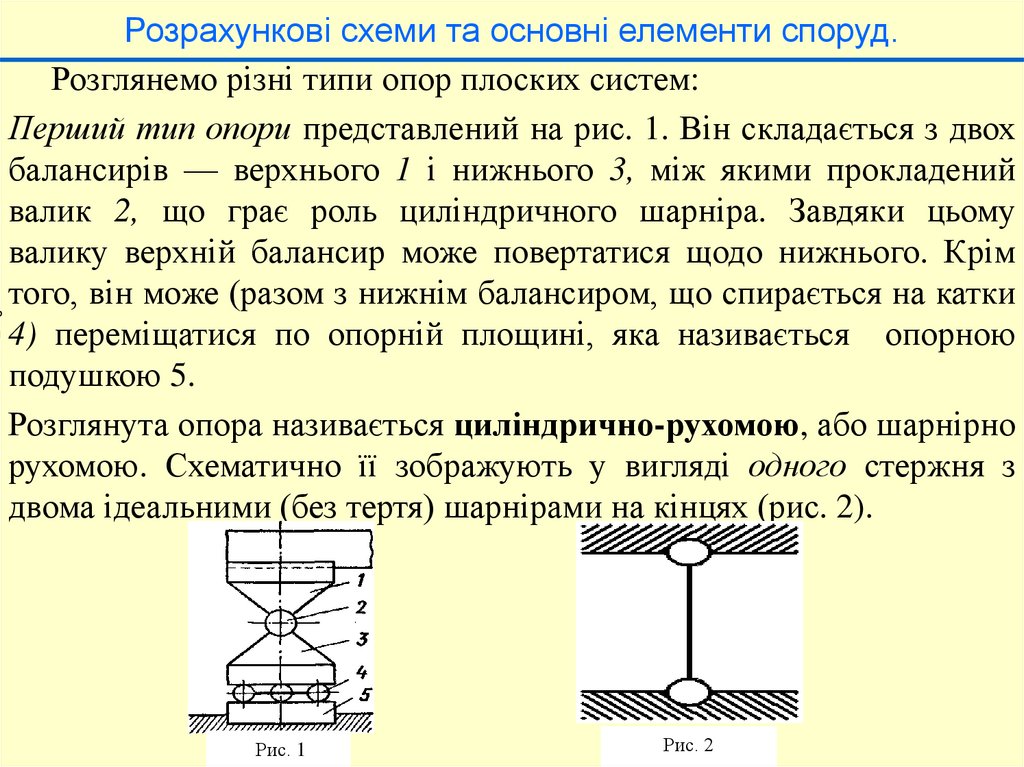
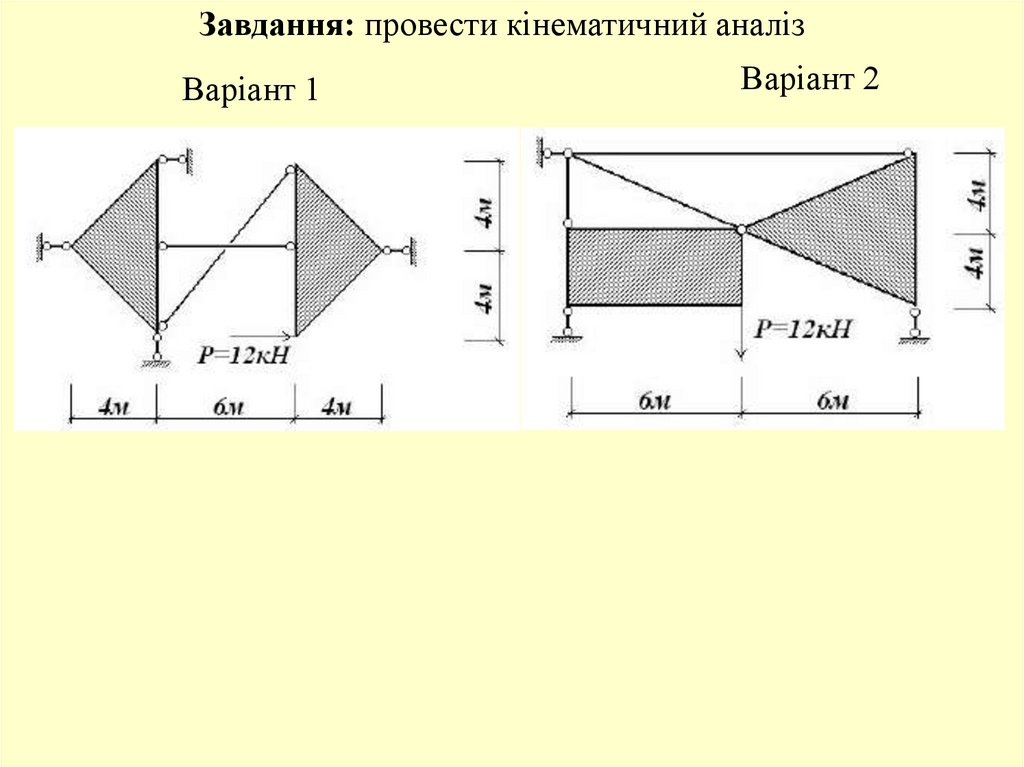
Завдання: провести кінематичний аналіз
Варіант 1
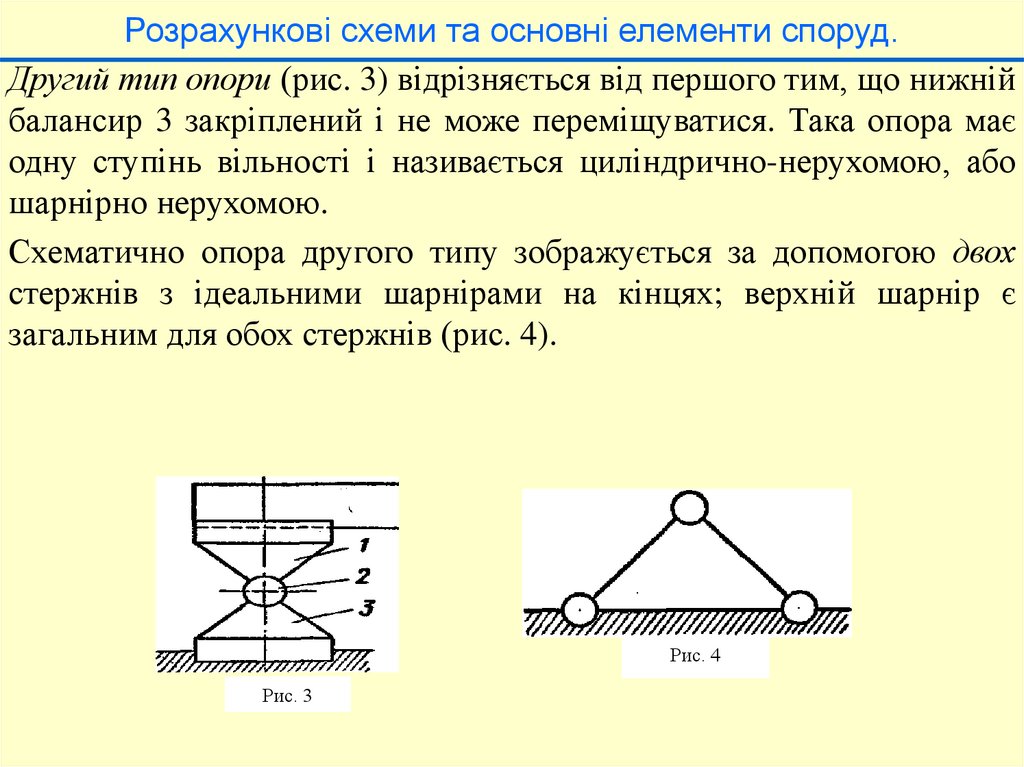
Варіант 2