Similar presentations:
Комплексные числа. Действия над комплексными числами в форме a+bi
1.
2.
Определение комплексныхчисел. Действия над
комплексными числами в
форме a+bi.
3.
4.
5.
6.
7.
8.
9.
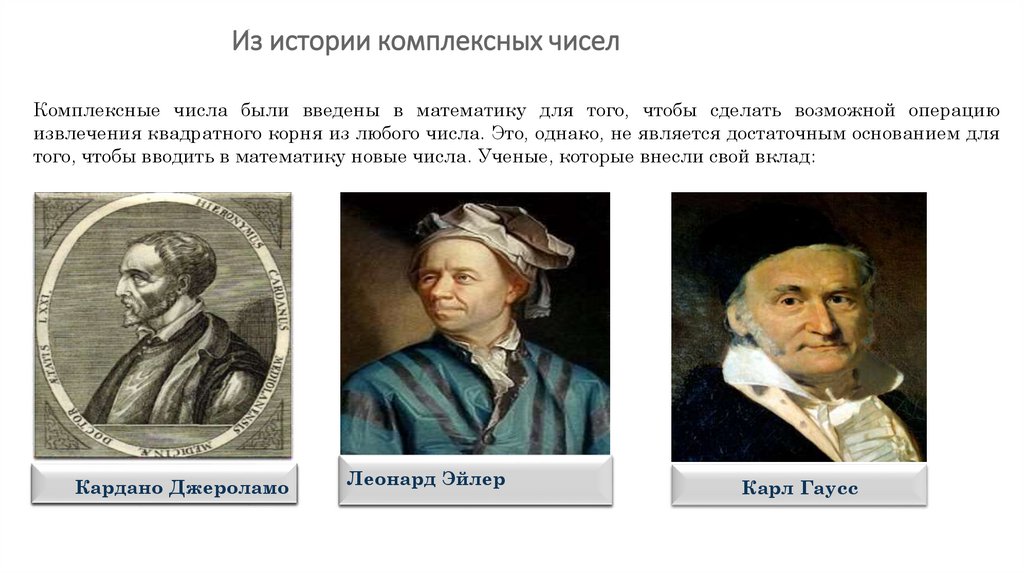
Из истории комплексных чиселКомплексные числа были введены в математику для того, чтобы сделать возможной операцию
извлечения квадратного корня из любого числа. Это, однако, не является достаточным основанием для
того, чтобы вводить в математику новые числа. Ученые, которые внесли свой вклад:
Кардано Джероламо
Леонард Эйлер
Карл Гаусс
10.
-In the set of real numbers, negative numbers donot have square roots.
-Imaginary numbers were invented so that negative
numbers would have square roots and certain
equations would have solutions.
-These numbers were devised using an imaginary
unit named i.
i 1
11.
-The imaginary numbers consist of all numbers bi,where b is a real number and i is the imaginary unit,
with the property that i² = -1.
2i
Example: 6i, -3i, , πi
5
12.
Powers of ii i
1
i 1
2
1.) Find i23
2.) Find i2006
3.) Find i37
4.) Find i828
i i
3
i
1
i
1
i 1
4
13.
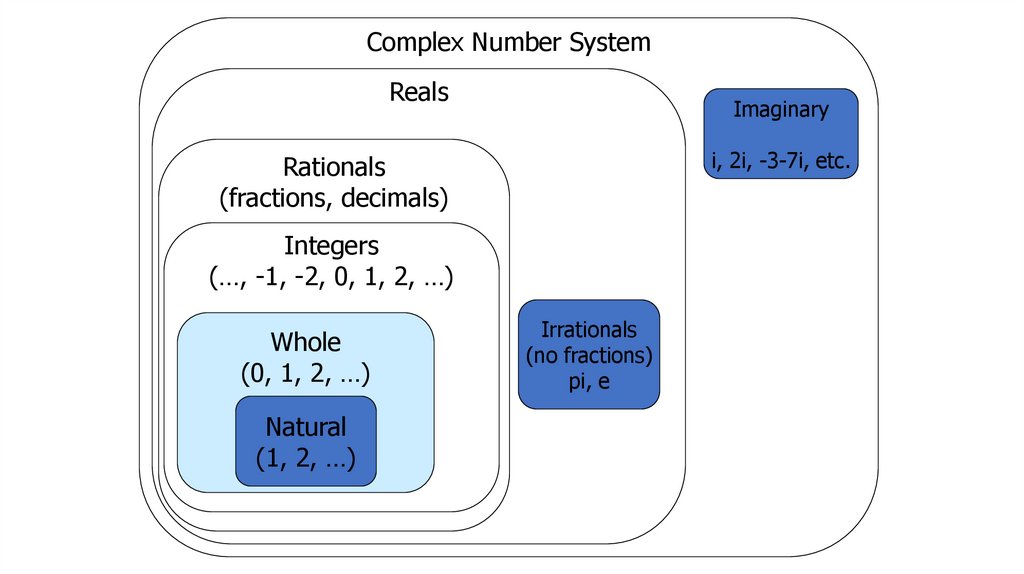
Complex Number SystemReals
Imaginary
i, 2i, -3-7i, etc.
Rationals
(fractions, decimals)
Integers
(…, -1, -2, 0, 1, 2, …)
Whole
(0, 1, 2, …)
Natural
(1, 2, …)
Irrationals
(no fractions)
pi, e
14.
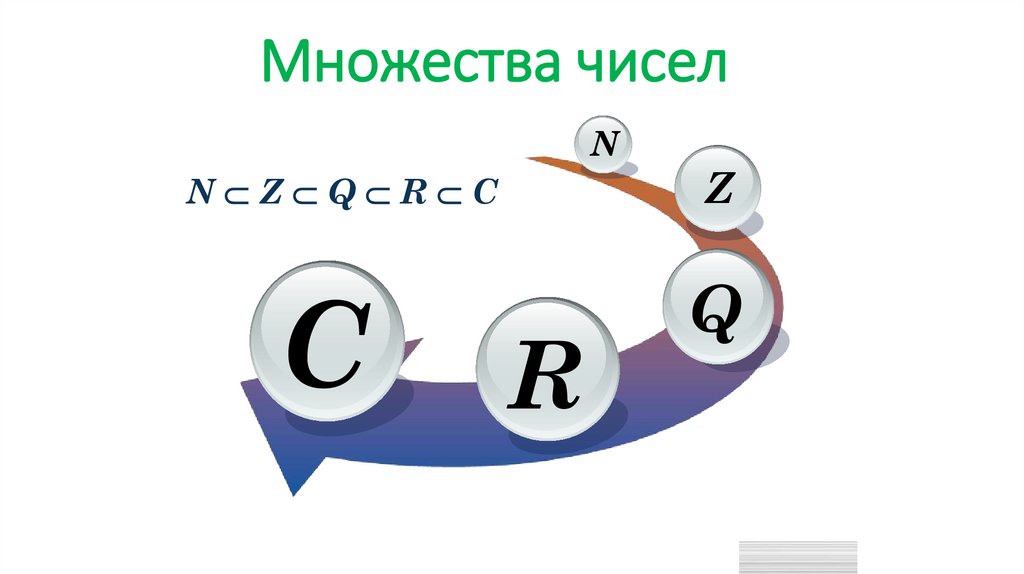
Множества чиселN
N Z Q R C
Z
С
Q
R
15.
Complex Numbersa + bi
real
imaginary
The complex numbers consist of all sums a + bi,
where a and b are real numbers and i is the imaginary
unit. The real part is a, and the imaginary part is b.
16.
Понятие комплексного числаКомплексные числа C – это пара (a; b) действительных чисел с
заданными определенным образом операциями умножения и
сложения.
Комплексное число z = (a; b) записывают как z = a + bi.
i2 = −1, i – мнимая единица.
Число Re z называется действительной частью числа z,
а число Im z – мнимой частью числа z.
Их обозначают a и b соответственно: a = Re z, b = Im z.
Определение:
Числа вида a + bi, где a и b – действительные числа, i – мнимая
единица, называются комплексными.
17.
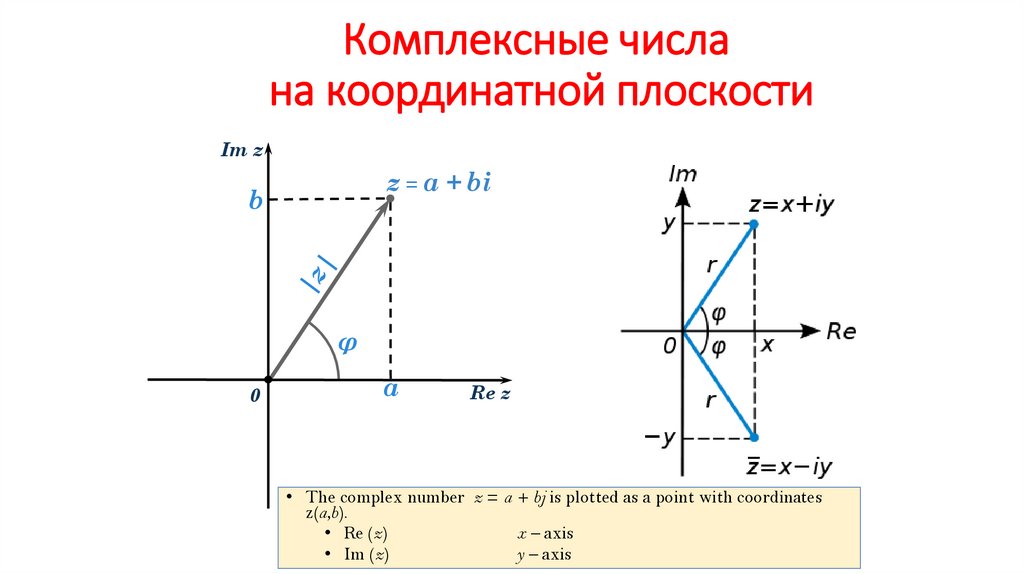
Комплексные числана координатной плоскости
Im z
z = a + bi
b
φ
0
a
Re z
• The complex number z = a + bj is plotted as a point with coordinates
z(a,b).
• Re (z)
x – axis
• Im (z)
y – axis
18.
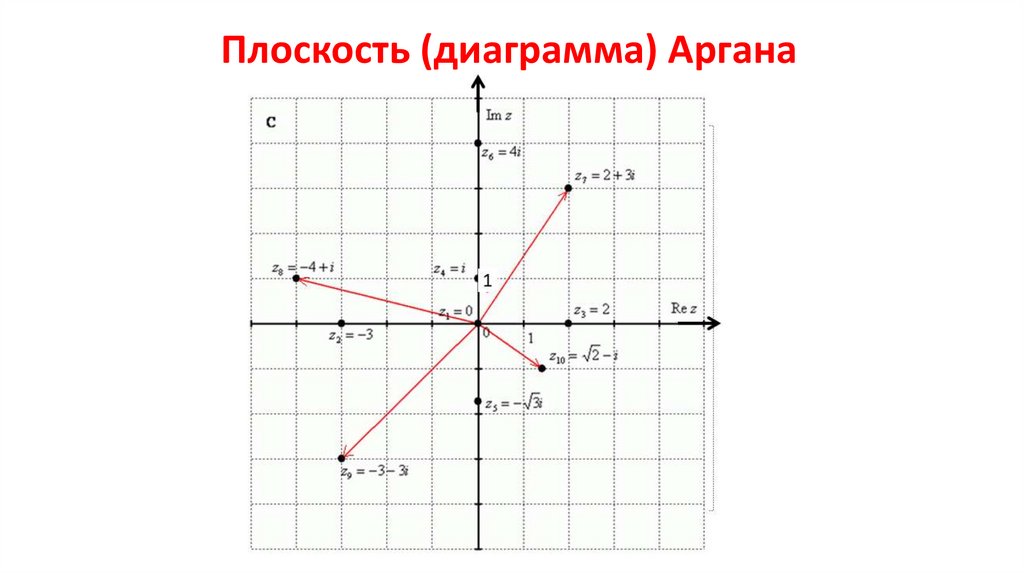
Плоскость (диаграмма) Аргана19.
The Complex Plane / Argand Diagram• Modulus of Complex Numbers
The modulus of z is defined by
r z a 2 b 2
20.
21.
Найдите модуль и аргументкомплексного числа:
1)
















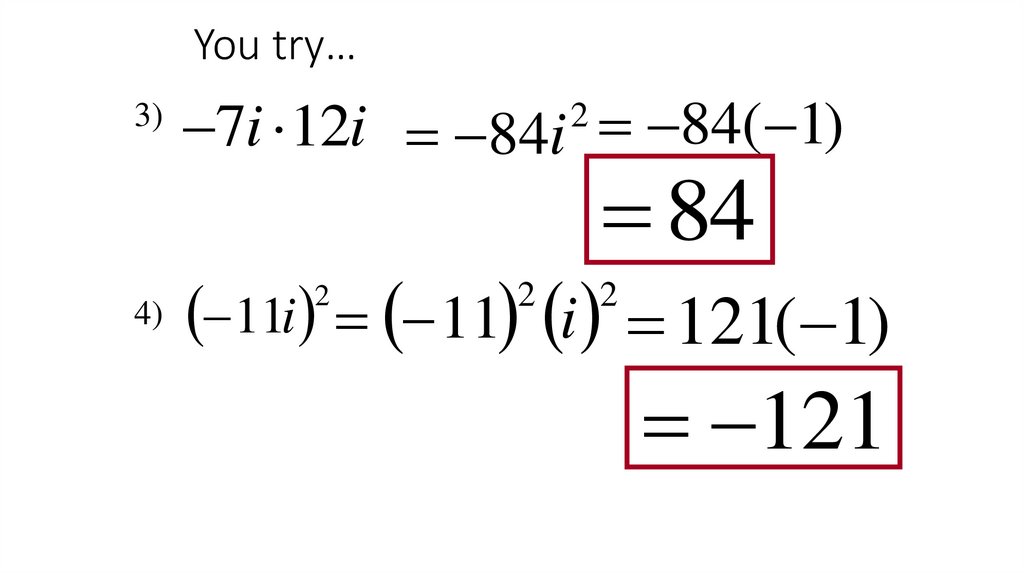


















 mathematics
mathematics








