Similar presentations:
Дерево отрезков. Персистентный массив. Алгоритмы и структуры данных
1.
Дерево отрезковПерсистентный массив
Алгоритмы и структуры данных
УрФУ, ФИИТ
2.
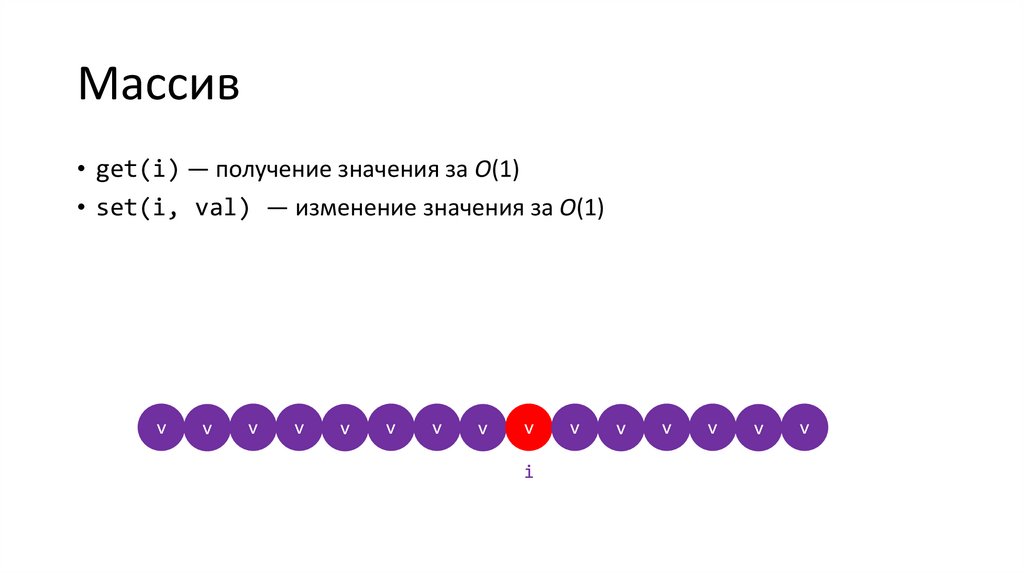
Массив• get(i) — получение значения за O(1)
• set(i, val) — изменение значения за O(1)
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
3.
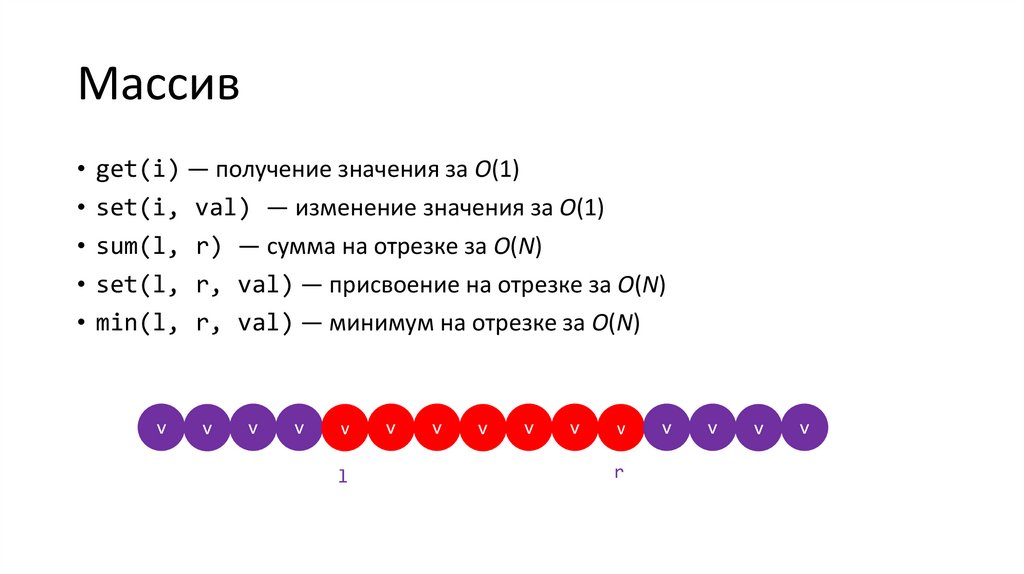
Массив• get(i) — получение значения за O(1)
• set(i, val) — изменение значения за O(1)
v
v
v
v
v
v
v
v
v
i
v
v
v
v
v
v
4.
Массив• get(i) — получение значения за O(1)
• set(i, val) — изменение значения за O(1)
• sum(l, r) — сумма на отрезке за O(N)
• set(l, r, val) — присвоение на отрезке за O(N)
• min(l, r, val) — минимум на отрезке за O(N)
v
v
v
v
v
l
v
v
v
v
v
v
r
v
v
v
v
5.
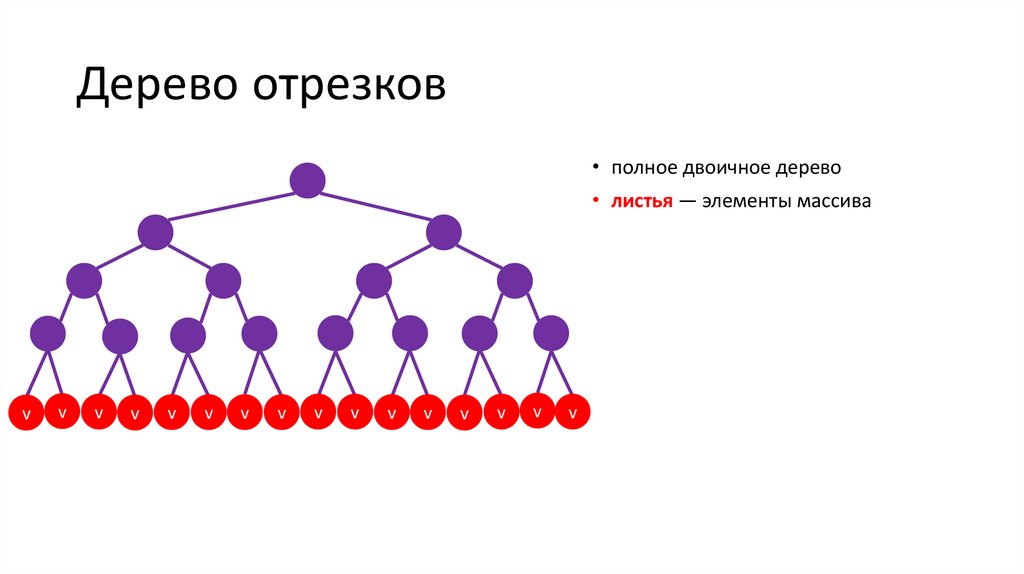
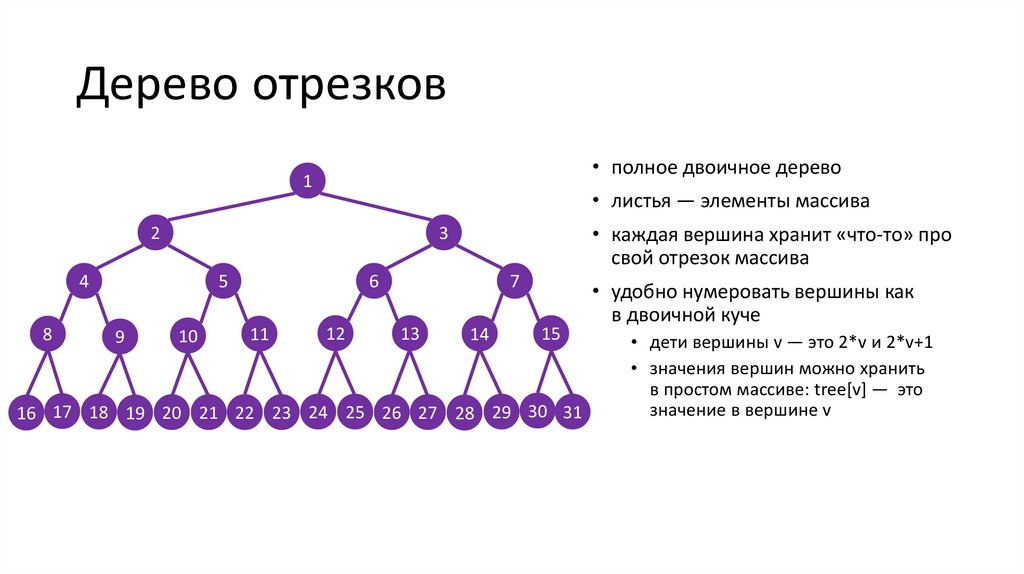
Дерево отрезков6.
Дерево отрезков• полное двоичное дерево
• листья — элементы массива
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
7.
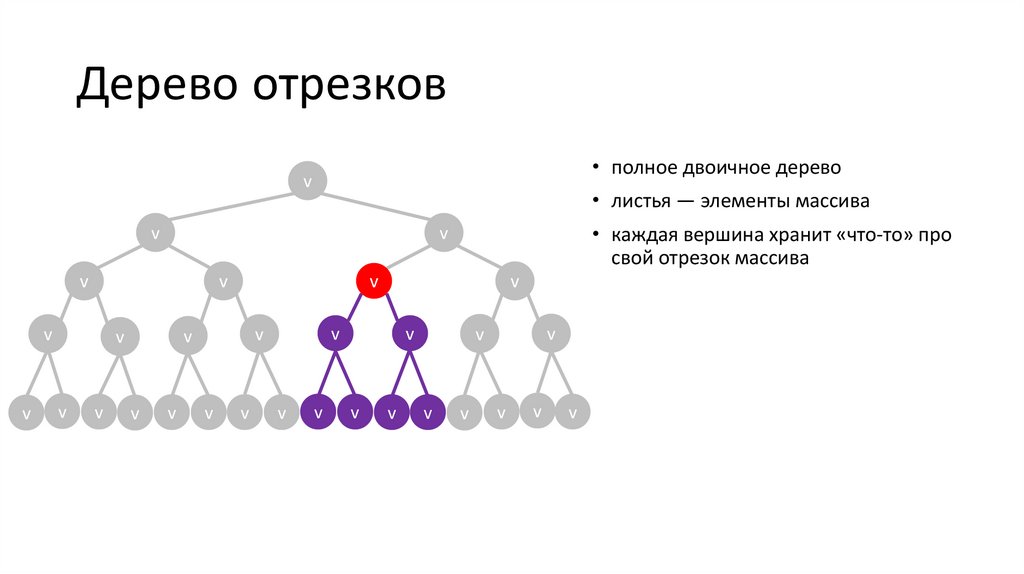
Дерево отрезков• полное двоичное дерево
v
• листья — элементы массива
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
v
• каждая вершина хранит «что-то» про
свой отрезок массива
v
v
v
v
v
v
v
v
v
v
v
v
v
8.
Дерево отрезков• полное двоичное дерево
1
• листья — элементы массива
2
4
8
5
9
• каждая вершина хранит «что-то» про
свой отрезок массива
3
10
6
11
12
7
13
14
15
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
• удобно нумеровать вершины как
в двоичной куче
• дети вершины v — это 2*v и 2*v+1
• значения вершин можно хранить
в простом массиве: tree[v] — это
значение в вершине v
9.
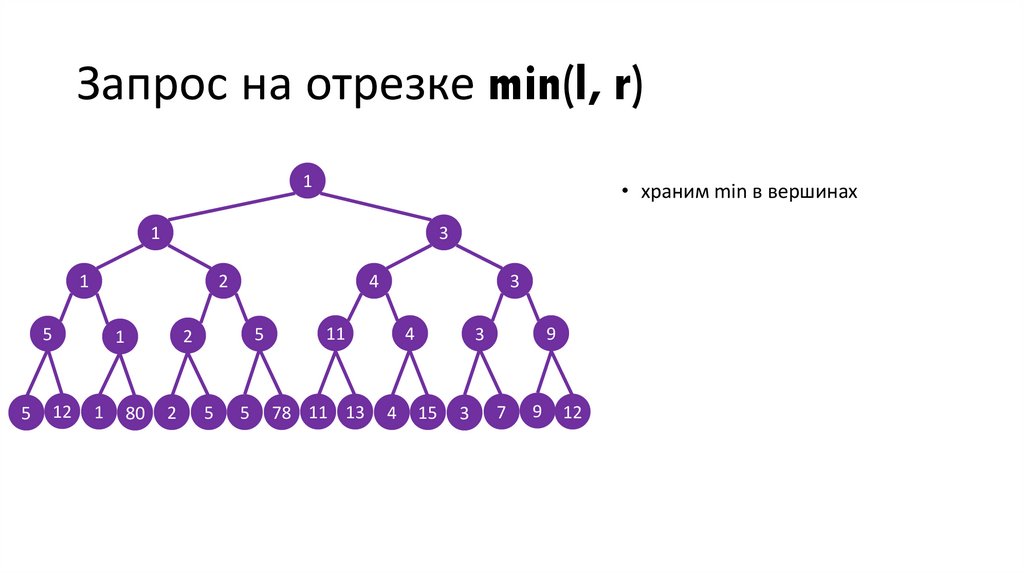
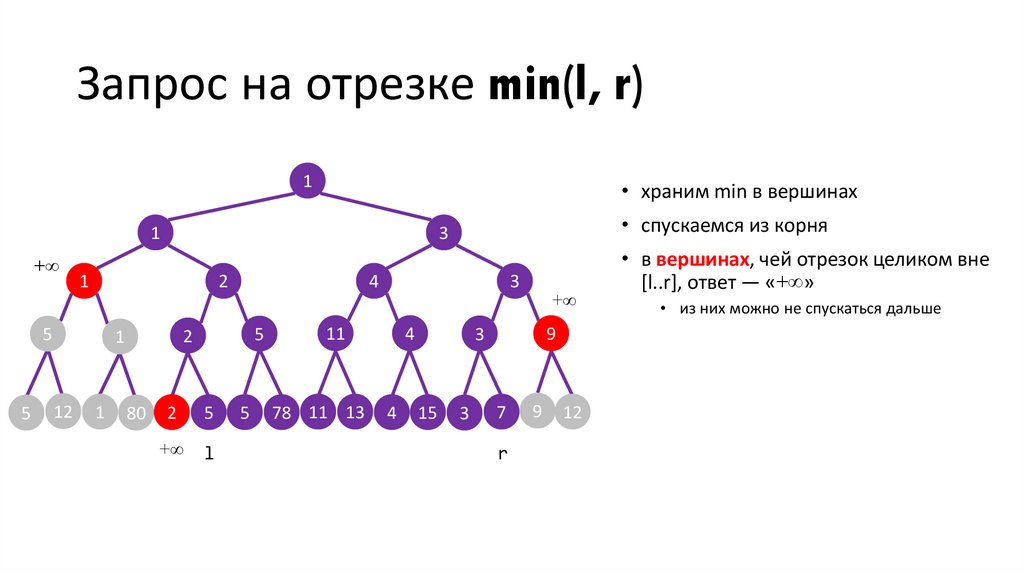
Запрос на отрезке min(l, r)1
• храним min в вершинах
1
3
1
2
5
5
12
5
2
1
1
4
80
2
5
5
3
11
78 11 13
4
4
9
3
15
3
7
9
12
10.
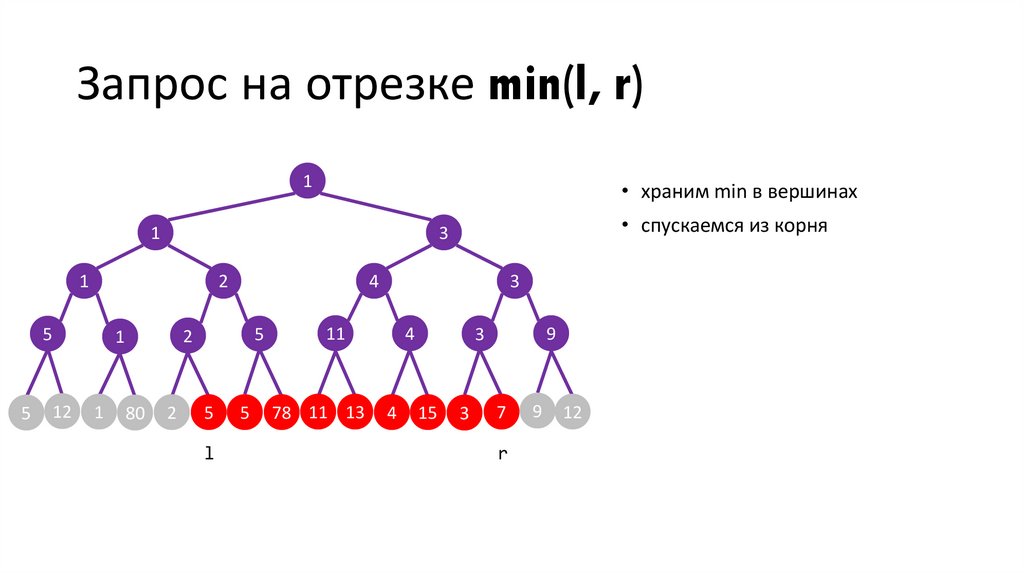
Запрос на отрезке min(l, r)1
• храним min в вершинах
1
1
2
5
5
12
4
5
2
1
1
80
• спускаемся из корня
3
2
5
l
5
3
11
78 11 13
4
4
9
3
15
3
7
r
9
12
11.
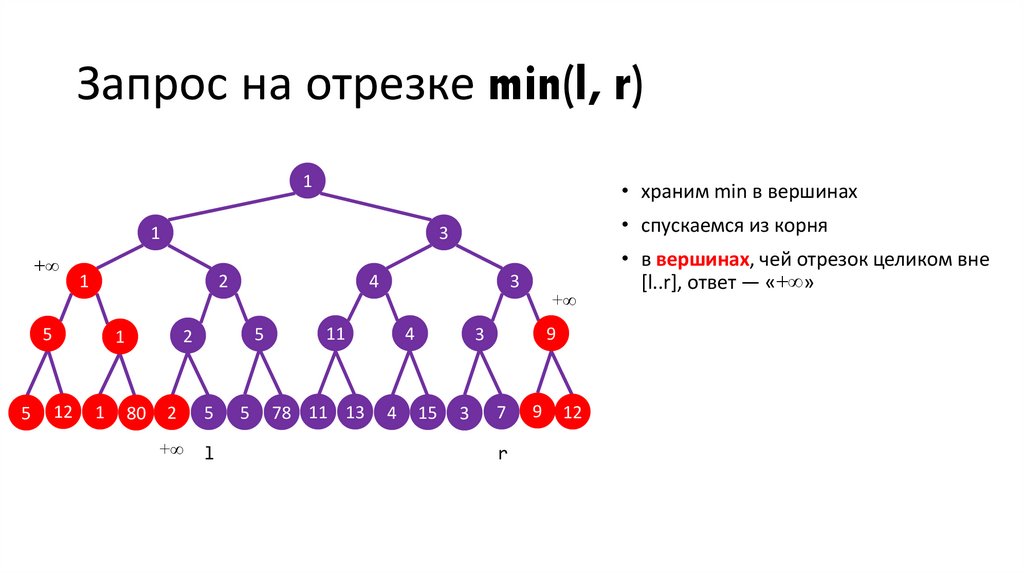
Запрос на отрезке min(l, r)1
• храним min в вершинах
1
+∞
1
2
5
5
1
4
5
2
1
12
80
• спускаемся из корня
3
2
5
+∞
l
5
3
11
78 11 13
4
4
+∞
9
3
15
3
7
r
9
12
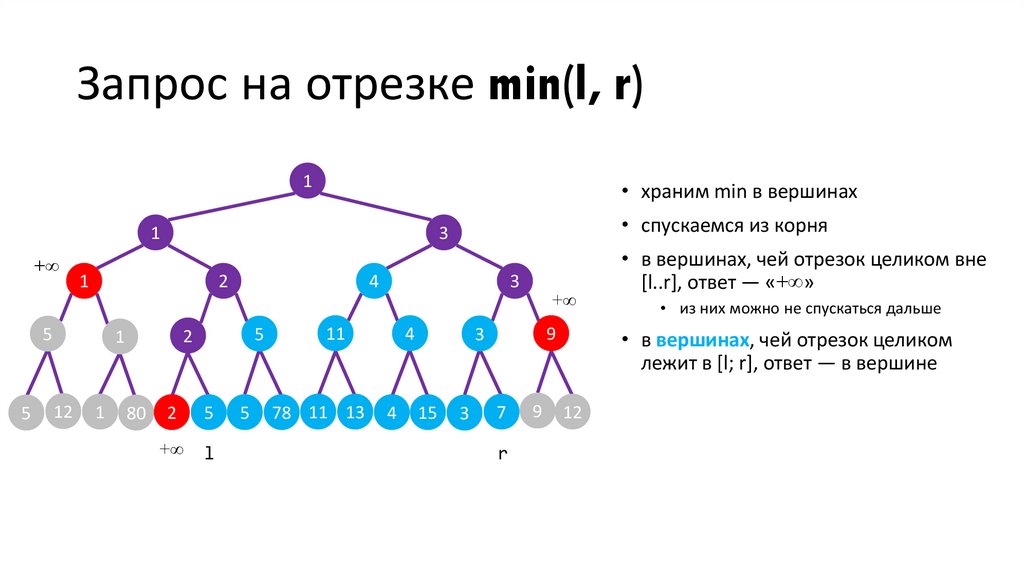
• в вершинах, чей отрезок целиком вне
[l..r], ответ — «+∞»
12.
Запрос на отрезке min(l, r)1
• храним min в вершинах
1
+∞
1
2
5
5
1
4
5
2
1
12
80
• спускаемся из корня
3
2
5
+∞
l
5
3
11
78 11 13
4
4
+∞
9
3
15
3
7
r
9
12
• в вершинах, чей отрезок целиком вне
[l..r], ответ — «+∞»
• из них можно не спускаться дальше
13.
Запрос на отрезке min(l, r)1
• храним min в вершинах
1
+∞
1
2
5
5
1
4
5
2
1
12
80
• спускаемся из корня
3
2
5
+∞
l
5
3
11
78 11 13
4
4
+∞
9
3
15
3
7
r
9
• в вершинах, чей отрезок целиком вне
[l..r], ответ — «+∞»
• из них можно не спускаться дальше
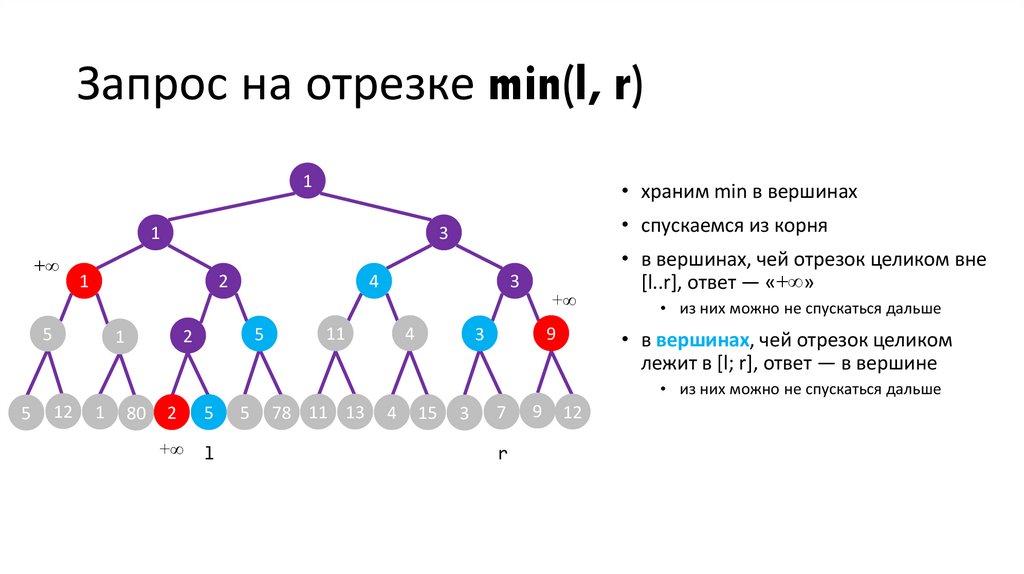
• в вершинах, чей отрезок целиком
лежит в [l; r], ответ — в вершине
12
14.
Запрос на отрезке min(l, r)1
• храним min в вершинах
1
+∞
1
2
5
• спускаемся из корня
3
4
5
2
1
3
11
4
+∞
9
3
• в вершинах, чей отрезок целиком вне
[l..r], ответ — «+∞»
• из них можно не спускаться дальше
• в вершинах, чей отрезок целиком
лежит в [l; r], ответ — в вершине
• из них можно не спускаться дальше
5
12
1
80
2
5
+∞
l
5
78 11 13
4
15
3
7
r
9
12
15.
Запрос на отрезке min(l, r)3
1
1
+∞
• спускаемся из корня
3
5
1
• храним min в вершинах
3
5
2
3
4
3
+∞
5
5
5
2
1
11
4
9
3
• в вершинах, чей отрезок целиком вне
[l..r], ответ — «+∞»
• из них можно не спускаться дальше
• в вершинах, чей отрезок целиком
лежит в [l; r], ответ — в вершине
• из них можно не спускаться дальше
5
12
1
80
2
5
+∞
l
5
78 11 13
4
15
3
7
r
9
12
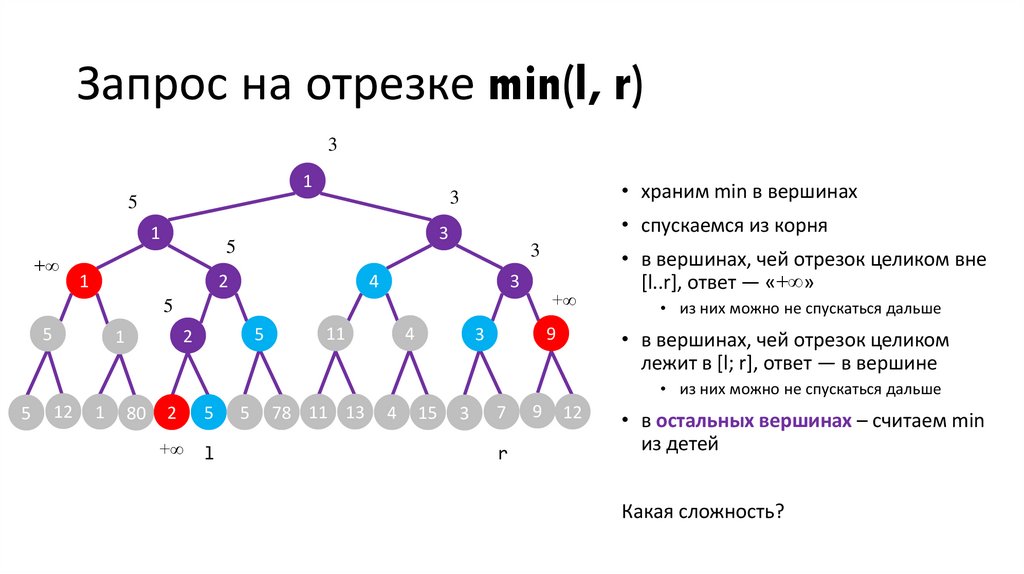
• в остальных вершинах – считаем min
из детей
Какая сложность?
16.
Запрос на отрезке min(l, r)// v — номер вершины, отвечающей за отрезок [tl, tr]
int get_min(int v, int tl, int tr, int l, int r) {
if (tl < l || r < tr) // отрезок вершины не пересекается с запросом
return INF;
if (l <= tl && tr <= r)
// отрезок вершины внутри отразка запроса
return tree_min[v];
int vm = (tl + tr) / 2;
return min(get_min(2*v,
tl,
vm, l, r),
get_min(2*v+1, vm+1, tr, l, r));
}
17.
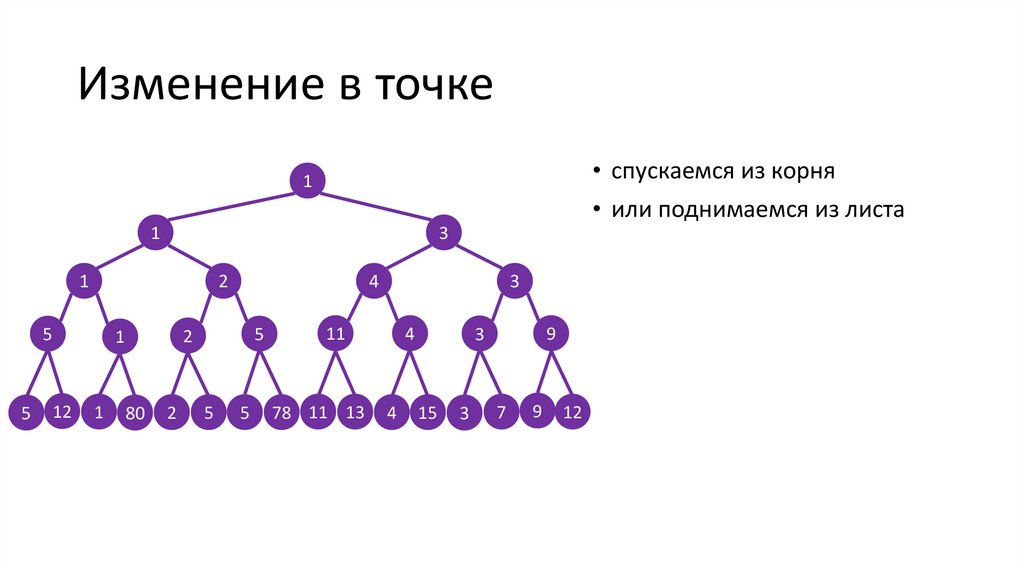
Изменение в точке• спускаемся из корня
• или поднимаемся из листа
1
1
3
1
2
5
5
12
5
2
1
1
4
80
2
5
5
3
11
78 11 13
4
4
9
3
15
3
7
9
12
18.
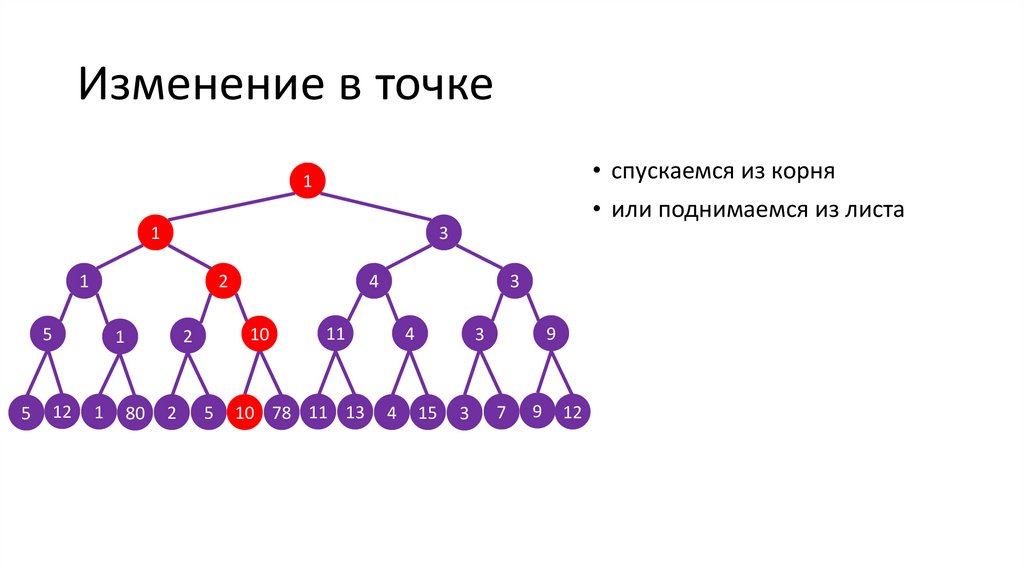
Изменение в точке• спускаемся из корня
• или поднимаемся из листа
1
1
3
1
2
5
5
12
1
10
2
1
80
2
4
5
3
11
10 78 11 13
4
4
9
3
15
3
7
9
12
19.
Изменение в точке// v — номер вершины, отвечающей за отрезок [tl, tr]
void set_val(int v, int tl, int tr, int pos, int val) {
if (tr < pos || pos < tl) return;
if (pos == tl && tr == pos) {
tree_min[v] = val;
return;
}
int tm = (tl + tr) / 2;
set_val(2*v,
tl,
tm, pos, val);
set_val(2*v+1, tm+1, tr, pos, val);
tree_min[v] = min(tree_min[2 * v], tree_min[2 * v + 1]);
}
20.
Изменение в точке// v — номер вершины, отвечающей за отрезок [tl, tr]
void set_val(int v, int tl, int tr, int pos, int val) {
if (tr < pos || pos < tl) return;
if (pos == tl && tr == pos) {
tree_min[v] = val;
return;
}
int tm = (tl + tr) / 2;
set_val(2*v,
tl,
tm, pos, val);
set_val(2*v+1, tm+1, tr, pos, val);
update(v); // обобщили!
}
21.
Дерево отрезков. Итого• Запрос операции на отрезке и изменение в точке — O(logN)
• Нужна ассоциативность операции запроса
22.
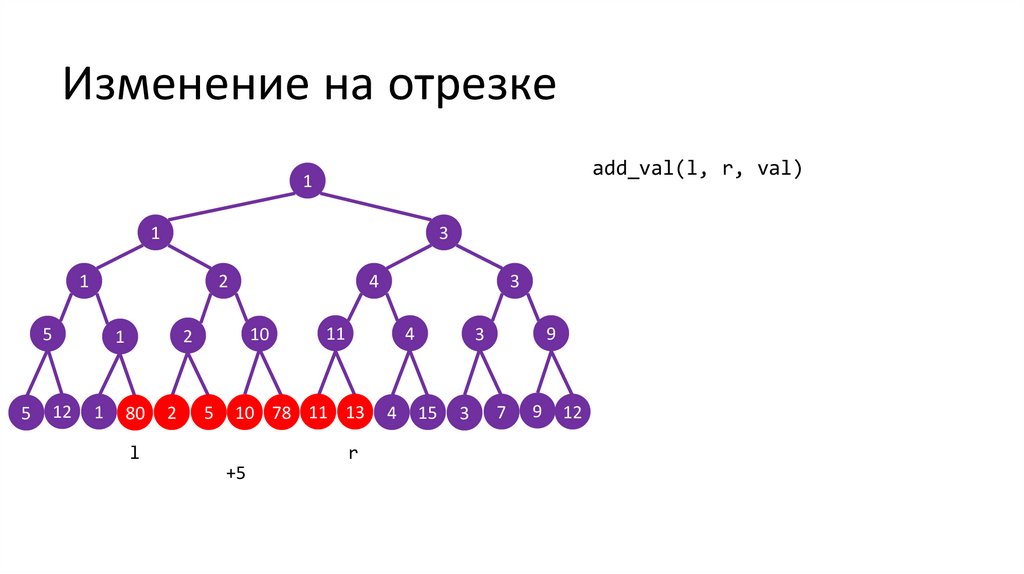
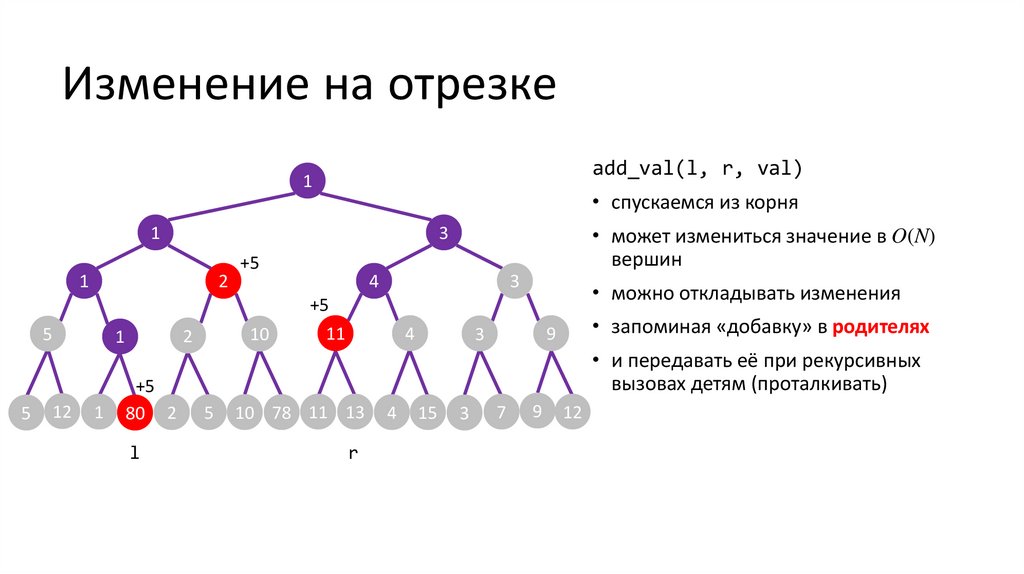
Изменение на отрезкеadd_val(l, r, val)
1
1
3
1
2
5
5
12
10
2
1
1
4
80
2
5
11
4
10 78 11 13
l
r
+5
3
4
9
3
15
3
7
9
12
23.
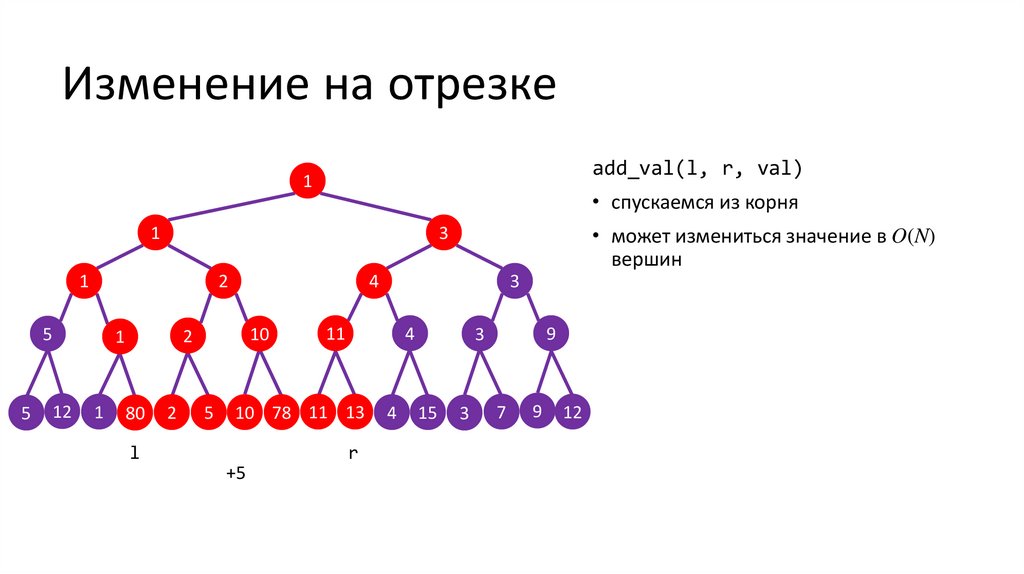
Изменение на отрезкеadd_val(l, r, val)
1
• спускаемся из корня
1
1
2
5
5
12
4
10
2
1
1
80
• может измениться значение в O(N)
вершин
3
2
5
11
4
10 78 11 13
l
r
+5
3
4
9
3
15
3
7
9
12
24.
Изменение на отрезкеadd_val(l, r, val)
1
• спускаемся из корня
1
1
2
5
5
12
1
+5
80 2
l
+5
10
2
1
• может измениться значение в O(N)
вершин
3
4
3
+5
11
4
• можно откладывать изменения
• запоминая «добавку» в родителях
9
3
• и передавать её при рекурсивных
вызовах детям (проталкивать)
5
10 78 11 13
r
4
15
3
7
9
12
25.
Изменение на отрезке// v — номер вершины, отвечающей за отрезок [tl, tr]
void add_val(int v, int tl, int tr, int l, int r, int val) {
if (tr < l || r < tl) return;
if (l <= tl && tr <= r) {
delay_add(v, val); // откладываем изменение
return;
}
push_add(v); // проталкиваем изменение перед рекурсией
int tm = (tl + tr) / 2;
add_val(2*v,
tl,
tm, l, r, val);
add_val(2*v+1, tm+1, tr, l, r, val);
update(v);
}
Инварианты:
1. Значение в текущей вершине корректно
2. Изменение к текущей вершине применено
3. К детям изменение не применено
26.
Изменение на отрезкеvoid delay_add(int v, int val) {
tree_min[v] += val;
tree_add[v] += val;
}
void push_add(int v) {
delay_add(2*v,
tree_add[v]);
delay_add(2*v+1, tree_add[v]);
tree_add[v] = 0;
}
27.
Дерево отрезков. Итого• Запрос операции и изменения на отрезке — O(logN)
• Нужна ассоциативность операции запроса
• Нужна дистрибутивность операции изменения относительно операции
запроса
28.
Персистентный массив29.
Обычный массивget(i) — получение значения
set(i, val) — изменение значения
30.
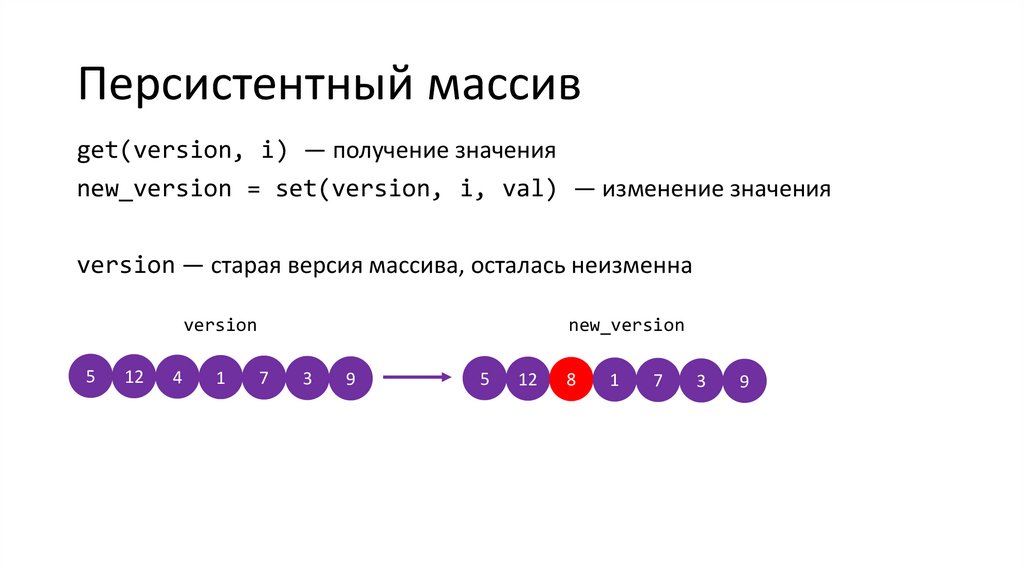
Персистентный массивget(version, i) — получение значения
new_version = set(version, i, val) — изменение значения
version — старая версия массива, осталась неизменна
version
5
12
4
1
new_version
7
3
9
5
12
8
1
7
3
9
31.
Наивные реализацииget(version, i) — получение значения
new_version = set(version, i, val) — изменение значения
1. Копировать массив на каждое изменение
• изменение O(N)
• запрос O(1)
2. Хранить дерево изменений (хранить diff на ребрах)
• изменение O(1)
• запрос O(N)
32.
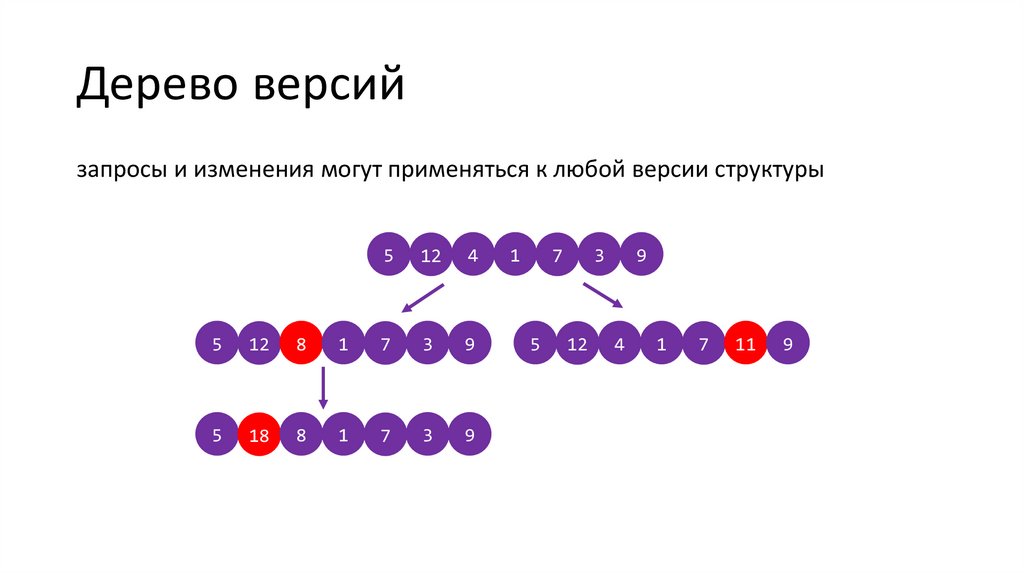
Дерево версийзапросы и изменения могут применяться к любой версии структуры
5
12
4
5
12
8
1
7
3
9
5
18
8
1
7
3
9
1
3
7
5
12
9
4
1
7
11
9
33.
Идея реализации• Сделаем дерево отрезков над массивом персистентным
• Будем пересоздавать изменившиеся узлы, и не менять не изменившиеся.
• Трюк с v*2 и v*2+1 для получения детей больше не будет работать
34.
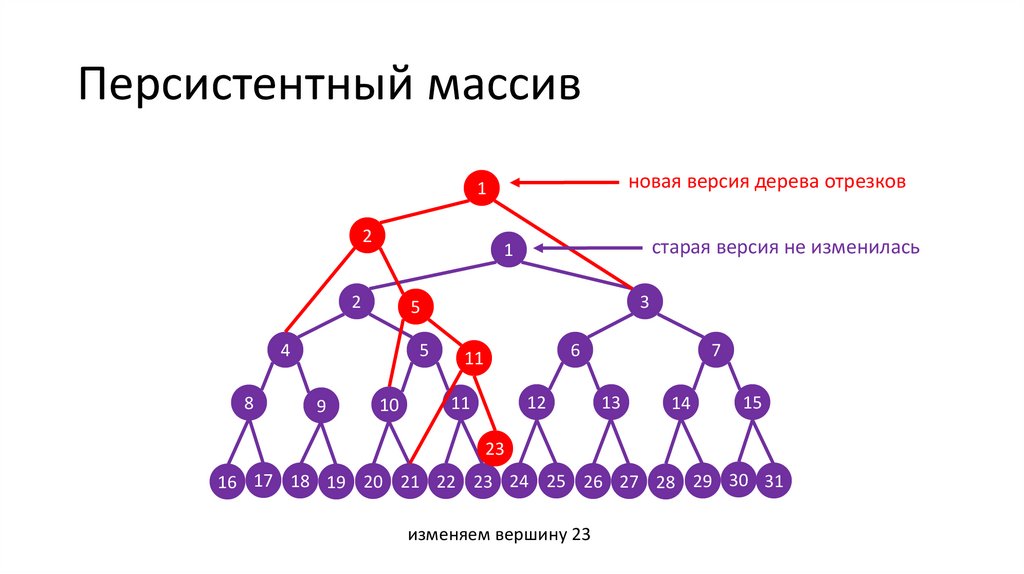
Персистентный массивновая версия дерева отрезков
1
2
2
5
9
3
5
4
8
старая версия не изменилась
1
10
6
11
12
11
7
13
14
15
23
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
изменяем вершину 23
35.
Изменение в точке// v — номер вершины, отвечающей за отрезок [tl, tr]
// возвращает новую версию вершины v
int set_val(int v, int tl, int tr, int pos, int val) {
if (tr < pos || pos < tl) return v;
new_v = copy_node(v);
if (pos == tl && tr == pos) {
tree_val[new_v] = val; return new_v;
}
int tm = (tl + tr) / 2;
left_child[new_v]
= set_val(left_child[new_v],
tl,
tm, pos, val);
right_child[new_v] = set_val(right_child[new_v], tm+1, tr, pos, val);
return new_v;
}
36.
Персистентныеструктуры данных
Любая структура данных, основанная на массивах превращается
в персистентную при переходе на персистентные массивы вместо обычных
• за дополнительный O(logN) времени (спуск по дереву)
• и за дополнительный O(logN) памяти (создаем новые узлы в дереве)
Во многих случаях от O(logN) можно избавиться, с применив аналогичную
идею с копированием изменившихся узлов
37.
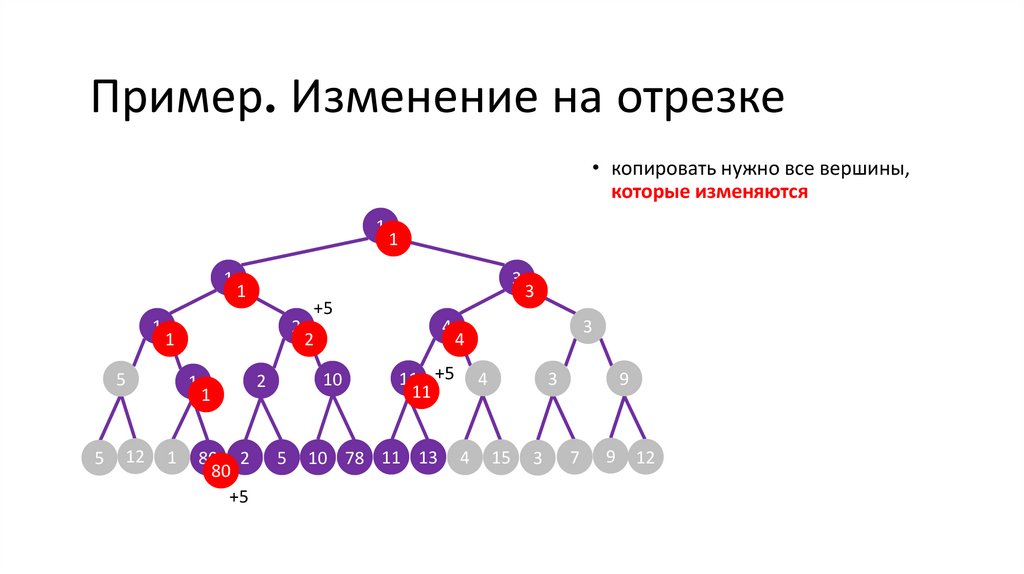
Пример. Изменение на отрезке• копировать нужно все вершины,
которые изменяются
1
1
1
5
12
3
1
2
1
5
1
1
1
80 2
80
+5
1
+5
10
2
5
4
2
3
4
11 +5
11
10 78 11 13
3
4
4
9
3
15
3
7
9
12
38.
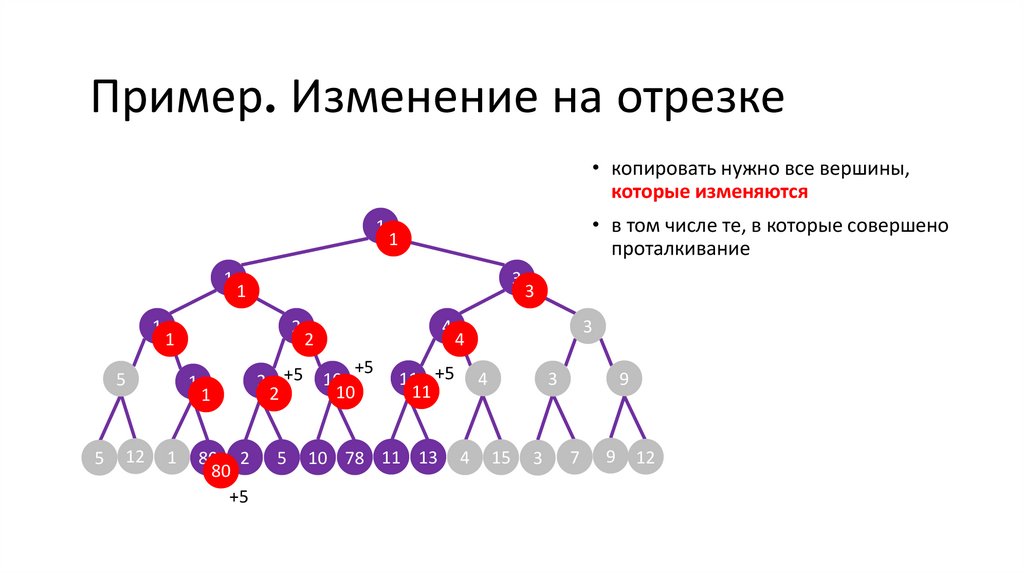
Пример. Изменение на отрезке• копировать нужно все вершины,
которые изменяются
1
1
1
5
12
3
1
2
1
5
1
1
• в том числе те, в которые совершено
проталкивание
1
1
80 2
80
+5
2 +5
2
5
4
2
+5
10
10
3
4
11 +5
11
10 78 11 13
3
4
4
9
3
15
3
7
9
12
















 programming
programming








