Принятие решений в конфликтных ситуациях на основе теории игр. Занятие № 11.9

1.

Тема № 11
«Принятие решений в
конфликтных ситуациях
на основе теории игр»
Занятие № 11.9
«Решение задач
статистических игр с
использованием различных
критериев»

2.

1. Обсуждение постановки задачи
2. Решение задачи
3. Анализ полученных результатов
и формулирование выводов

3.

П1
П2
П3
А1
0.2
0.3
0.15
А2
0.75
0.2
0.35
А3
0.25
0.8
0.25
А4
0.85
0.05
0.45
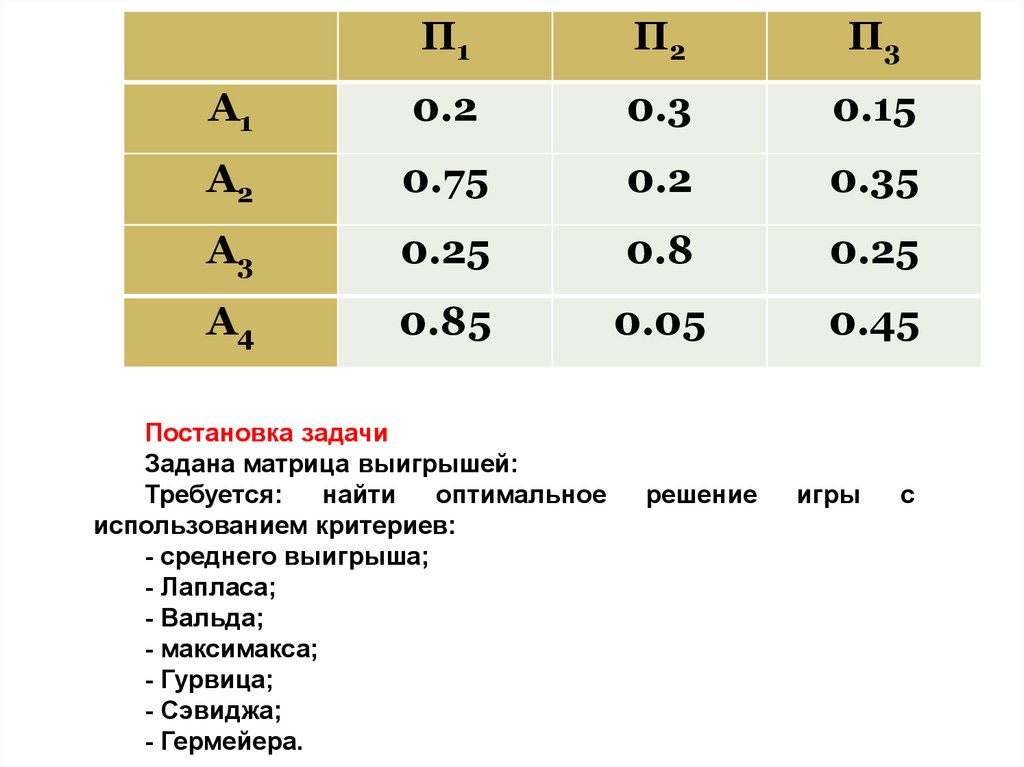
Постановка задачи
Задана матрица выигрышей:
Требуется:
найти
оптимальное
использованием критериев:
- среднего выигрыша;
- Лапласа;
- Вальда;
- максимакса;
- Гурвица;
- Сэвиджа;
- Гермейера.
решение
игры
с

4.

В этом учебном вопросе рекомендуется обсудить с
курсантами критерии оценки эффективности решений в
неопределенной операции, убедиться в понимании ими
сущности оценки по каждому критерию.
Оценку эффективности решений для неопределенной
операции проведем с использованием шести критериев:
- среднего выигрыша;
- Лапласа;
- Вальда;
- максимакса;
- Гурвица;
- Сэвиджа;
- Гермейера.
Расчеты по каждому критерию предполагает использование
соотношений:

5.

а) Критерий среднего выигрыша (для заданных значений
вероятностей p1, p2, p3, p4)
n
_____
U ( xi ) p jU ij , i 1, m .
j 1
U o max U ( xi ).
i
б) Критерий Лапласа:
_____
1 n
U ( xi ) U ij , i 1, m .
n j 1
U o max U ( xi ).
i

6.

в) Критерий Вальда:
_____
_____
U ( xi ) min U ij , i 1, m , j 1, n .
_____
U o max U ( xi ), i 1, m .
i
г) Критерий максимакса:
_____
U ( xi ) max U ij , j 1, n .
j
_____
_____
U o max(max U ij ), i 1, m , j 1, n .
i
j

7.

д) Критерий обобщенного максимина (Гурвица):
_____
U ( xi ) max U ij (1 ) min U ij , j 1, n .
j
j
_____
U o max U ij , i 1, m .
i
е) Критерий Сэвиджа:
_____
_____
U ij max U ij U ij , i 1, m , j 1, n ,
i
_____
U ( xi ) max U ij , j 1, n ,
j
_____
U o min U ( xi ), i 1, m .
i

8.

ж) Критерий Гермейера:
U ( xi ) p j u ij ;
i 1, m;
U o max min p j u ij ;
i
j
_____
_____
j 1, n.
_____
i 1, m;
Провести расчеты по выбранным
критериям.
_____
j 1, n.

9.

а) Определение
выигрыша.
Пусть:
p1 = 0,3;
p2 = 0,2;
p3 = 0,5
эффективности
решений
по
критерию
среднего
При расчетах используются значения матрицы эффективности,
представленные в таблице 9.
U(x1) = 0,3 * 0,2 + 0,2 * 0,3 + 0,5 * 0,15 = 0.06 + 0.15 + 0.075 = 0.285;
U(x2) = 0,3 * 0,75 + 0,2 * 0,2 + 0,5 * 0,35 = 0.225 + 0.04 + 0.175 = 0.44;
U(x3) = 0,3 * 0,85 + 0,2 * 0,8 + 0,5 * 0,25 = 0.255 + 0.16 + 0.125 = 0.54;
U(x4) = 0,2 * 0,043 + 0,2 * 0,05 + 0,5 * 0,45 = 0.0086 + 0.01 + 0.225 = 0.2436;
Uo = U(x3) = 0,54.

10.

б) Определение эффективности решений по критерию
Лапласа.
U(x1) = 0,33 * (0,2 + 0,3 + 0,15) = 0,33 * 0.65 = 0,2145;
U(x2) = 0,33 * (0,75 + 0,2 + 0,35) = 0,33 * 1.3 = 0,429;
U(x3) = 0,33 * (0,25 + 0,8 + 0,25) = 0,33 * 1.3 = 0,429;
U(x4) = 0,33 * (0,85 + 0,05 + 0,45) = 0,33 * 1.35 = 0,4455;
Uo = U(x4) = 0,4455.

11.

в) Определение эффективности решений по критерию
Вальда.
U(x1) = min (0,08; 0,055; 0,242; 0,335) = 0,055;
U(x2) = min (0,055; 0,045; 0,213; 0,334) = 0,045;
U(x3) = min (0,013; 0,032; 0,071; 0,143) = 0,013;
U(x4) = min (0,178; 0,127; 0,536; 0,723) = 0,127;
U(x5) = min (0,043; 0,096; 0,187; 0,325) = 0,043;
U(x6) = min (0,098; 0,098; 0,176; 0,287) = 0,098.
Uo = U(x4) = 0,127.

12.

г) Определение эффективности решений по критерию
максимакса.
U(x1) = max (0,08; 0,055; 0,242; 0,335) = 0,335;
U(x2) = max (0,055; 0,045; 0,213; 0,334) = 0,334;
U(x3) = max (0,013; 0,032; 0,071; 0,143) = 0,143;
U(x4) = max (0,178; 0,127; 0,536; 0,723) = 0,723;
U(x5) = max (0,043; 0,096; 0,187; 0,325) = 0,325;
U(x6) = max (0,098; 0,098; 0,176; 0,287) = 0,287.
Uo = U(x4) = 0,723.

13.

д) Определение эффективности решений по критерию
Гурвица (при α= 0,8).
U(x1) = 0,8 * 0,335 + (1 – 0,8) * 0,055 = 0,279;
U(x2) = 0,8 * 0,334 + (1 – 0,8) * 0,045 = 0,276;
U(x3) = 0,8 * 0,143 + (1 – 0,8) * 0,013 = 0,117;
U(x4) = 0,8 * 0,723 + (1 – 0,8) * 0,127 = 0,604;
U(x5) = 0,8 * 0,325 + (1 – 0,8) * 0,043 = 0,269;
U(x6) = 0,8 * 0,287 + (1 – 0,8) * 0,098 = 0,249.
Uo = U(x4) = 0,604.

14.

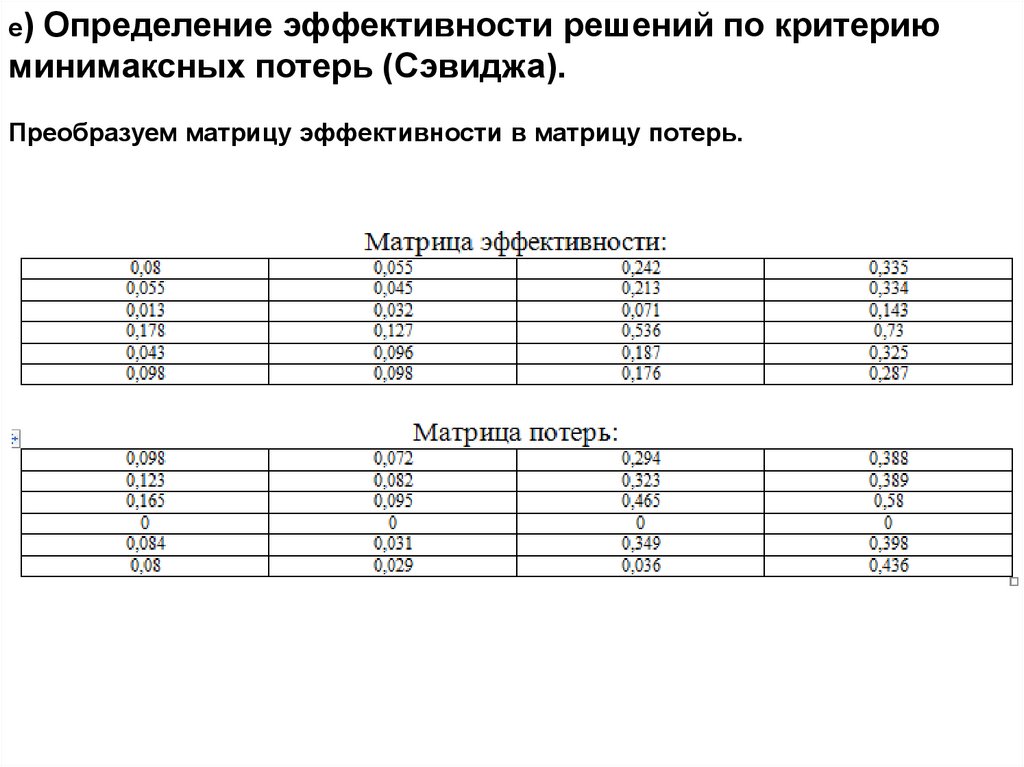
е) Определение эффективности решений по критерию
минимаксных потерь (Сэвиджа).
Преобразуем матрицу эффективности в матрицу потерь.

15.

U(x1) = max (0,098; 0,072; 0,294; 0,388) = 0,388;
U(x2) = max (0,123; 0,082; 0,323; 0,389) = 0,389;
U(x3) = max (0,165; 0,095; 0,465; 0,58) = 0,465;
U(x4) = max (0; 0; 0; 0) = 0;
U(x5) = max (0,084; 0,031; 0,349; 0,398) = 0,398;
U(x6) = max (0,08; 0,029; 0,036; 0,436) = 0,436.
Uo = U(x4) = 0.

16.

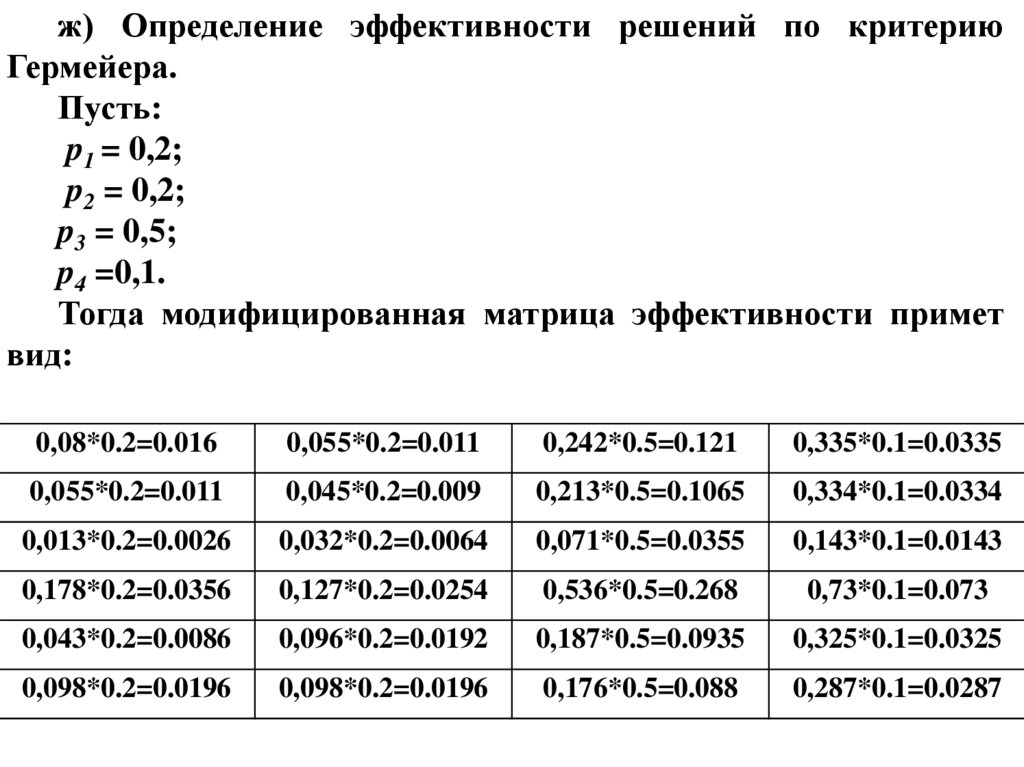
ж) Определение эффективности решений по критерию
Гермейера.
Пусть:
p1 = 0,2;
p2 = 0,2;
p3 = 0,5;
p4 =0,1.
Тогда модифицированная матрица эффективности примет
вид:
0,08*0.2=0.016
0,055*0.2=0.011
0,242*0.5=0.121
0,335*0.1=0.0335
0,055*0.2=0.011
0,045*0.2=0.009
0,213*0.5=0.1065
0,334*0.1=0.0334
0,013*0.2=0.0026
0,032*0.2=0.0064
0,071*0.5=0.0355
0,143*0.1=0.0143
0,178*0.2=0.0356
0,127*0.2=0.0254
0,536*0.5=0.268
0,73*0.1=0.073
0,043*0.2=0.0086
0,096*0.2=0.0192
0,187*0.5=0.0935
0,325*0.1=0.0325
0,098*0.2=0.0196
0,098*0.2=0.0196
0,176*0.5=0.088
0,287*0.1=0.0287

17.

U(x1) = min (0,016; 0,011; 0,121; 0,0335) = 0,011;
U(x2) = min (0,011; 0,009; 0,1065; 0,0334) = 0,009;
U(x3) = min (0,0026; 0,0064; 0,0355; 0,0143) = 0,0026;
U(x4) = min (0 ,0356; 0 ,0254; 0,268; 0,073) = 0,0254;
U(x5) = min (0,0086; 0,0192; 0,0935; 0,0325) = 0,0086;
U(x6) = min (0,0196; 0,0196; 0,088; 0,0287) = 0,0196.
Uo = U(x4) = 0,0254.

18.

19.

•По заданной матрице эффективности:
оценить эффективность решений и найти
оптимальное решение по критерию Лапласа.
Прокомментировать результат.
i / j
y1
y2
y3
y4
y5
x1
0.1
0.5
0.1
0.2
0.1
x2
0.2
0.3
0.2
0.4
0.3
x3
0.1
0.4
0.4
0.3
0.4

20.

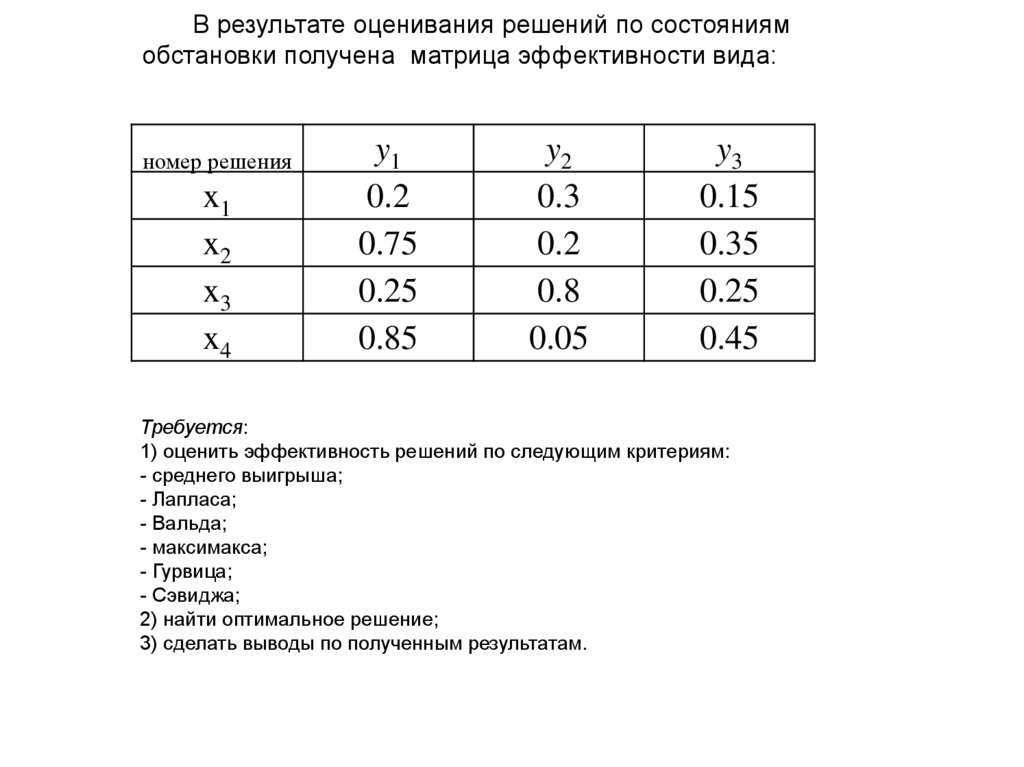
В результате оценивания решений по состояниям
обстановки получена матрица эффективности вида:
номер решения
x1
x2
x3
x4
y1
0.2
0.75
0.25
0.85
y2
0.3
0.2
0.8
0.05
y3
0.15
0.35
0.25
0.45
Требуется:
1) оценить эффективность решений по следующим критериям:
- среднего выигрыша;
- Лапласа;
- Вальда;
- максимакса;
- Гурвица;
- Сэвиджа;
2) найти оптимальное решение;
3) сделать выводы по полученным результатам.