Физическая химия. О чём этот предмет?

1.

Физическая химия
О чём этот предмет?
Физическая химия - это изучение макроскопических и
микроскопических явлений в химических системах с точки зрения
принципов и концепций физики, таких как:
движение, энергия, сила, время, термодинамика, квантовая механика,
статистическая механика,
применительно к:
квантовой химии, химическим равновесиям, кинетике и механизму
химических реакций, электрохимическим превращениям.
Лекции "Физическая химия, часть 1"
1

2.

Физическая химия
Основные разделы ФХ:
Строение вещества
Химическая термодинамика
Химическая кинетика
Учение о растворах
Электрохимия
Лекции "Физическая химия, часть 1"
2

3.

Физическая химия
Литература:
• Лефедова О.В., Немцева М.П. Основные понятия и определения дисциплин
«Физическая химия» и «Коллоидная химия» . Учебн. пособие. 2017. (Э)
• Федорова А.А., Лефедова О.В. Физическая и коллоидная химия.
Электронный курс лекций. (Э)
• Краткий справочник физико –химических величин. Под ред. Равделя
А.А., Пономаревой Л.М.
• И.В. Кудряшов, Г.С. Каретников. Сборник примеров и задач по физической
химии. - М. : ВШ. -1991.
• Практикум по физической химии. Под ред. Буданова В.В., Воробьева Н.К.
1986.
• Физическая химия. Под ред. Краснова К.С. Учебник. Том I и II. 2001
• А.Г. Стромберг, Д.П. Семченко. Физическая химия. Учебник. 1988.
• Поленов Ю.В., Егорова Е.В., Егорова К.О., Физическая химия. Часть I.
Электронный учебник. 2011 (Э)
• Поленов Ю.В., Егорова Е.В. Кинетика химических реакций. Учебное пособие.
2010 (Э)
Лекции "Физическая химия, часть 1"
3

4.

Записываемся на курс в
Moodle:
кодовое слово:
Лекции "Физическая химия, часть 1"
4

5.

Раздел 1. Химическая термодинамика
Химическая термодинамика – раздел физической химии, в
котором изучаются превращения различных видов энергии,
сопровождающие всевозможные химические процессы.
Объектами исследования химической термодинамики являются
только системы, состоящие из очень большого количества
микрочастиц, так называемые макроскопические системы.
Только в таких системах можно оперировать понятиями
температура, давление, теплота.
Лекции "Физическая химия, часть 1"
5

6.

Химическая термодинамика
Химическая термодинамика:
• НЕ рассматривает механизм протекания процесса
• В термодинамике отсутствует понятие «время»
• В
термодинамике
рассматриваются
характеристики
начального и конечного состояния системы, но НЕ сам
процесс
• Термодинамика
изучает
химических процессов
энергетические
эффекты
• Термодинамика позволяет определить направленность и
глубину протекания химического процесса
Лекции "Физическая химия, часть 1"
6

7.

Химическая термодинамика
Термодинамической системой называют любое тело или
совокупность тел, способных обмениваться между собой и с
окружающей средой энергией и веществом.
Термодинамические системы могут быть:
• открытыми, т.е. обмениваться энергией и веществом;
• закрытыми, в которых невозможен обмен веществом, но
возможен энергией
• изолированными, в которых исключен обмен и энергией, и
веществом.
• Фазой называется совокупность однородных частей системы,
ограниченная поверхностью.
Системы бывают:
• гомогенными (однофазными), если между частями системы
нет поверхностей раздела
• гетерогенными, если поверхности раздела присутствуют.
Лекции "Физическая химия, часть 1"
7

8.

Химическая термодинамика
Совокупность физических и химических свойств системы называется
состоянием системы.
В термодинамике рассматриваются обычно те свойства, которые
можно выразить через измеряемые на опыте величины, так
называемые параметры состояния:
температуру (Т); давление (р); объем (V); концентрации (С).
Параметры состояния связаны между собой уравнением состояния.
Пример: уравнение Менделеева – Клапейрона:
pV=nRT
где:
n − число молей (количество вещества)
R − универсальная газовая постоянная, R=8,314 Дж/(моль∙К)
Р − давление газа (Па),
V − объем газа (м3),
Т − температура (К)
Лекции "Физическая химия, часть 1"
8

9.

Химическая термодинамика
Термодинамические свойства разделяют на:
• экстенсивные, которые пропорциональны массе системы
(например, объем, теплоемкость, внутренняя энергия)
• интенсивные, не зависящие от массы (молярный объем,
температура, давление).
Если в термодинамической системе изменяется во времени хотя бы
одно из термодинамических свойств, то это означает, что в ней
протекает термодинамический процесс. Он может протекать:
•самопроизвольно, без затраты энергии извне (например,
диффузия, растворение веществ)
•несамопроизвольно (например, выделение газов на электродах
при электролизе, разделение воздуха на кислород и азот).
Лекции "Физическая химия, часть 1"
9

10.

Химическая термодинамика
Кроме того, термодинамические процессы разделяют на:
• равновесные (квазистатические) - протекают бесконечно
медленно через непрерывный ряд состояний, близких к
равновесными
• неравновесные (неквазистатические).
Полезная работа в равновесном процессе максимальна, а
затраченная - минимальна.
Если ход прямого и обратного процессов совпадает, и в системе и в
окружающей среде не наблюдается никаких изменений, то процесс
является термодинамически обратимым.
Лекции "Физическая химия, часть 1"
10

11.

Химическая термодинамика
Первый закон термодинамики
При протекании термодинамических процессов может совершаться
полезная работа. Работу будем обозначать W.
Например, при расширении газа в цилиндре под поршнем
совершается работа по перемещению поршня в определенном
направлении.
Таким образом, работа является упорядоченной формой передачи
энергии от одной системы (газ) к другой (поршень).
Причем величина работы зависит от вида процесса, т.е. работа –
функция процесса.
Работа, выполняемая системой против внешних сил, считается
положительной.
Лекции "Физическая химия, часть 1"
11

12.

Химическая термодинамика
Первый закон термодинамики
Другой способом передачи энергии от одной системы к другой − в
форме теплоты (Q), т.е. за счет беспорядочного столкновения молекул
о границу раздела систем.
Теплота также является функцией процесса.
Теплота, полученная системой, считается положительной, а отданная
внешнему миру – отрицательной.
Теплота и работа передаются за счет энергии частиц системы.
Совокупность всех видов энергии частиц в системе называется
внутренней энергией (U).
Она включает в себя: поступательную и вращательную энергию
молекул, колебательную – атомов и групп атомов, энергию движения
электронов, внутриядерную энергию, энергию взаимодействия всех
частиц между собой.
Внутренняя энергия является частью полной энергии.
U является функцией состояния системы, то есть зависит только от
начального и конечного состояния системы, но не от пути процесса.
Лекции "Физическая химия, часть 1"
12

13.

Химическая термодинамика
Первый закон термодинамики
Взаимосвязь между теплотой, работой и внутренней энергией
устанавливается первым законом термодинамики.
Этот закон, в свою очередь, является следствием закона сохранения
энергии.
Если к системе подвести какое-либо количество тепла, то оно
пойдет на изменение внутренней энергии системы и
совершение системой работы.
Математическая закона запись закона имеет вид:
Q=ΔU + W
где Q – количество теплоты; U – внутренняя энергия; W – работа.
Лекции "Физическая химия, часть 1"
13

14.

Химическая термодинамика
Первый закон термодинамики
Q=ΔU + W
Для бесконечно малых приращений:
где pdV – работа расширения;
W’- другие виды работ (электрическая, поверхностная и т.д.).
Обратите внимание на различные значки: d и δ:
• энергия и объем могут иметь изменение (приращение):
бесконечно малые d или измеряемые Δ,
• теплота и работа характеризуются «порциями» переданной
теплоты Q (или δQ) или совершенной работы W (или δW). А
понятие «изменение» к этим понятиям неприменимы.
Лекции "Физическая химия, часть 1"
14

15.

Химическая термодинамика
Первый закон термодинамики
Если другие виды работ отсутствуют, то:
Функция
Н = U + pV
называется энтальпией.
Так как U является функцией состояния, а изменения параметров p и V
зависят от их начальных и конечных значений, то Н − также функция
состояния.
Для изолированной системы Q = 0 и W = 0, так как обмен энергией в
любой форме с окружающей средой отсутствует, то dU = 0 и U = const,
то есть:
Запас внутренней энергии изолированной системы есть
величина постоянная
Лекции "Физическая химия, часть 1"
15

16.

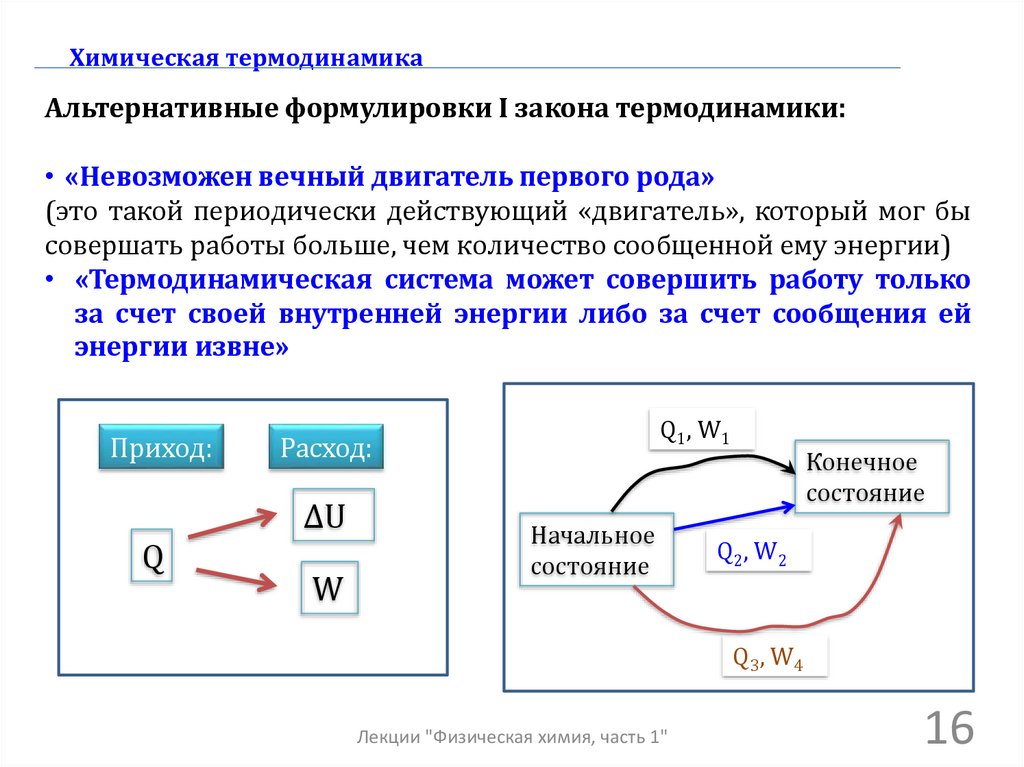
Химическая термодинамика
Альтернативные формулировки I закона термодинамики:
• «Невозможен вечный двигатель первого рода»
(это такой периодически действующий «двигатель», который мог бы
совершать работы больше, чем количество сообщенной ему энергии)
• «Термодинамическая система может совершить работу только
за счет своей внутренней энергии либо за счет сообщения ей
энергии извне»
Приход:
ΔU
Q
Q1, W1
Расход:
W
Начальное
состояние
Конечное
состояние
Q2, W2
Q3, W4
Лекции "Физическая химия, часть 1"
16

17.

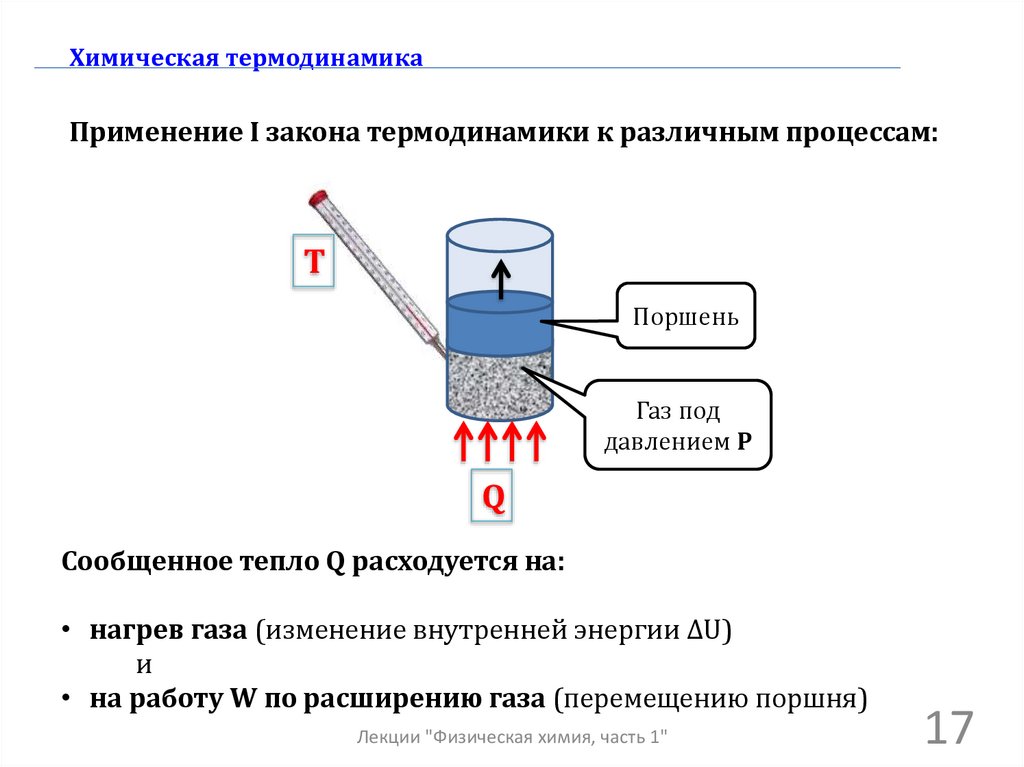
Химическая термодинамика
Применение I закона термодинамики к различным процессам:
Т
Поршень
Газ под
давлением Р
Q
Сообщенное тепло Q расходуется на:
• нагрев газа (изменение внутренней энергии ΔU)
и
• на работу W по расширению газа (перемещению поршня)
Лекции "Физическая химия, часть 1"
17

18.

Химическая термодинамика
Применение I закона термодинамики к различным процессам:
1) Изохорный процесс (V=const):
изохорном
процессе
δW=PdV ⇒ WV = 0 (т.к. dV=0) При
подводимое тепло идет только на
QV= ΔU или δQV= dU
нагрев
2) Изотермический процесс (Т=const):
U
i m
RT (для ид. газа)
2M
QT = W или δQТ=δW
⇒ U=const при Т=const ⇒ ΔU=0
При изотермическом процессе
подводимое тепло идет только на
работу расширения
Лекции "Физическая химия, часть 1"
18

19.

Химическая термодинамика
Применение I закона термодинамики к различным процессам:
3) Изобарный процесс (Р=const):
δW=PdV⇒ WР = РΔV (т.к. P=const) ⇒ QP= ΔU +PΔV
или с учетом уравнения Менделеева-Клапейрона:
i 2 m
i 2
QP
R T
или QP
P V
При изобарном процессе
2 M
2
тепловым эффектом
является изменение
или QP= Δ(U+PV) = ΔH
QP= ΔU+PΔV
энтальпии
4) Адиабатический процесс (Q=0):
0 = ΔU + W
W =−ΔU
или
δW =− dU
При адиабатическом процессе
система может совершать работу
только за счет (см. знак минус)
запаса внутренней энергии
Лекции "Физическая химия, часть 1"
19

20.

Химическая термодинамика
Формулы работы,
совершаемой идеальным газом в различных процессах
Процесс
Работа
Изохорный
WV = 0
Изотермический
m
V2 m
P1
WT
RT Ln
RT Ln
M
V1 M
P2
Изобарный
WP
Адиабатический
m 2
W
CV dT
M T1
m
RΔT PΔV
M
T
Лекции "Физическая химия, часть 1"
W
m
CV (T1 T2 )
M
20

21.

Химическая термодинамика
Закон Гесса. Тепловой эффект химической реакции
Раздел химической термодинамики, в котором изучаются процессы,
связанные с поглощением или выделением тепла, называется
термохимией.
Тепловые эффекты необходимы для расчетов тепловых балансов и для
исследования химического равновесия.
Предположим, что в идеальной газовой смеси протекает химическая
реакция согласно стехиометрическому уравнению:
ν1, ν2, ν3, ν4 стехиометрические
коэффициенты
Если в результате реакции прореагируют исходные веществ, и получатся
продукты реакции в стехиометрических количествах, то говорят, что
реакция совершила один пробег.
При отсутствии других видов работ, кроме работы расширения, можно
найти выражение для расчета теплоты, проинтегрировав уравнение:
V2
Q U PdV
V1
Лекции "Физическая химия, часть 1"
21

22.

Химическая термодинамика
Закон Гесса. Тепловой эффект химической реакции
Напомним, что при V = const QV = ΔU; при p = const QP = ΔU+pΔV=ΔH.
Для химической реакции теплоты QР и QV – тепловые эффекты при
постоянных давлении и объеме соответственно.
Введем понятие теплового эффекта химической реакции
Тепловым эффектом химической реакции называют количество теплоты,
которое выделяется (поглощается) при следующих условиях:
- реакция совершает один пробег;
- давление или объем постоянны;
- все другие виды работ, кроме работы расширения, отсутствуют;
- продукты реакции имеют ту же температуру, что и исходные вещества.
Лекции "Физическая химия, часть 1"
22

23.

Химическая термодинамика
Закон Гесса
Так как внутренняя энергия и энтальпия являются функциями
состояния, то:
Тепловой эффект химической реакции не зависит от
пути процесса (промежуточных стадий), а определяется
только начальным и конечным состояниями системы
(это формулировка закона Гесса)
Лекции "Физическая химия, часть 1"
23

24.

Химическая термодинамика
Найдем связь между тепловыми эффектами изобарного и
изохорного процессов:
Qp − QV = (ΔU + pΔV ) − ΔU = pΔV
Для идеальной газовой смеси: pΔV = (Δν)RT
Тогда:
где Δν = (ν3+ν4) – (ν1 +ν2 )
Qp − QV = (Δν)RT
!!!! Если в реакции участвуют вещества в конденсированном состоянии,
то при расчете Δν их стехиометрические коэффициенты НЕ учитывают.!!!!
Пример. Для реакции:
С6H6(ж) + 7,5O2(газ) = 6CO2(газ) + 3H2O(ж)
Δν = (6+0) − (0+7,5) = − 1,5
Лекции "Физическая химия, часть 1"
24

25.

Химическая термодинамика
Поскольку чаще реакции проводят при Р=const, то будем под тепловым
эффектом реакции будем понимать ΔrH.
Вспомним правило знаков для теплового эффекта:
• для экзотермической реакции тепловой эффект считается
отрицательным (Δr H <0), так как энергия (теплота) выделяется из
системы,
• для эндотермической реакции тепловой эффект положителен (ΔrH >0),
так как энергия (теплота) поглощается из окружающей среды.
Закон Гесса дает возможность рассчитывать тепловые эффекты,
сопровождающие химические превращения. В термохимии наиболее
часто используют понятия теплот образования, сгорания и
растворения.
Лекции "Физическая химия, часть 1"
25

26.

Химическая термодинамика
Теплота образования (Δf H):
Под теплотой образования химического соединения понимают тепловой
эффект реакции образования 1 моль этого вещества из простых веществ,
взятых в устойчивом состоянии при рассматриваемых условиях.
(простыми называют вещества, состоящие из атомов одного хим. элемента,
например, С(граф.), О2, Н2, …)
Теплота сгорания(ΔСH):
Под теплотой сгорания химического соединения понимают тепловой
эффект реакции полного сгорания 1 моль этого вещества с образованием
продуктов определенного состава.
Продуктами полного сгорания являются CO2, Н2О(ж), N2, SO2, HCl и т.д.
Теплота растворения (Δраств.H):
Под теплотой растворения химического соединения понимают тепловой
эффект реакции полного растворения 1 моль этого вещества в
бесконечном количестве растворителя:
Δраств.H = Δкрист. реш.H + Δсольв.H
Лекции "Физическая химия, часть 1"
26

27.

Химическая термодинамика
В справочной литературе приводятся значения теплот образования и
сгорания при стандартных условиях: Т = 298,15 К и p = 1 атм, обозначения
которых ΔfH298о и Δс H298о.
Для простых веществ теплоты образования приняты равными нулю!
Расчеты тепловых эффектов возможны на основании следствий из закона Гесса:
Следствие 1:
Тепловой эффект реакции равен алгебраической сумме теплот
образования продуктов реакции за вычетом алгебраической суммы
теплот образования исходных веществ (с учетом стехиометрических
коэффициентов).
Δr H2980 = [ν3Δf H2980 (A3 ) + ν4Δf H2980 (A4 )] - [ν1Δf H2980 (A1 ) + ν2Δf H2980 (A2 )]
Следствие 1:
Тепловой эффект реакции равен алгебраической сумме теплот сгорания
исходных веществ за вычетом алгебраической суммы теплот сгорания
продуктов реакции (с учетом стехиометрических коэффициентов).
Δr H2980 = [ν1Δc H2980 (A1 ) + ν2Δc H2980 (A2 )] - [ν3Δc H2980 (A3 ) + ν4Δc H2980 (A4 )]
Лекции "Физическая химия, часть 1"
27

28.

Химическая термодинамика
Δr H2980 = [ν3Δf H2980 (A3 ) + ν4Δf H2980 (A4 )] - [ν1Δf H2980 (A1 ) + ν2Δf H2980 (A2 )]
Пример.
Для реакции
С6H6(ж) + 7,5O2(газ) = 6CO2(газ) + 3H2O(ж)
расчет теплоты реакции по следствию из закона Гесса запишется следующим
образом:
ΔrH2980 = [6ΔfH298о(CO2(газ))+3Δf H298о(H2O(ж))]−[1ΔfH298о(С6H6(ж))+7,5ΔfH298о (O2(газ))]
Продукты реакции
Исходные вещества
В справочнике вы найдете, что для простого вещества ΔfH298о (O2(газ))=0,
поскольку кислород в форме вещества O2 в газообразном состоянии при 298
К является наиболее устойчивой формой кислорода.
Для другой формы кислорода, озона O3, ΔfH298о(O3(газ))=142 кДж/моль,
она менее устойчива, чем O2(газ) при 298 К и 1 атм.
Лекции "Физическая химия, часть 1"
28

29.

Химическая термодинамика
Зависимость теплового эффекта реакции от температуры.
Уравнения Кирхгоффа
Кроме расчета теплового эффекта реакции при стандартной
температуре (298,15 К), часто возникает необходимость расчета тепловых
эффектов при других температурах. Для этого используют зависимость
теплоемкости вещества от температуры.
Под средней теплоемкостью в интервале температур ΔТ понимают
отношение конечного количества теплоты, затраченного на нагревание
единицы массы (или количества) вещества, к разности температур:
С
Q
m T
С
Q
n T
− средняя удельная теплоемкость, Дж/(кг∙К)
− средняя молярная теплоемкость, Дж/(моль∙К),
n – число молей
Лекции "Физическая химия, часть 1"
29

30.

Химическая термодинамика
Зависимость теплового эффекта реакции от температуры.
Уравнения Кирхгоффа
Истинная теплоемкость – отношение бесконечно малого количества
теплоты δQ к бесконечно малому приращению температуры dT:
С
Q
− истинная молярная теплоемкость
ndT
В зависимости от условий определения различают теплоемкость при
постоянном давлении (СР) и постоянном объеме (СV).
Так как количество теплоты при постоянном объеме равно изменению
внутренней энергии, а при постоянном давлении – изменению энтальпии,
то истинные теплоемкости равны (в расчете на 1 моль):
U
H
СV
C
P
T
T
V
P
Связь между СР и СV (формула Майера):
СV CP R
Лекции "Физическая химия, часть 1"
30

31.

Химическая термодинамика
Зависимость теплового эффекта реакции от температуры.
Уравнения Кирхгоффа
Для расчетов необходимо знать значения теплоемкостей при различных
температурах. Их зависимости от температуры в имеются в справочниках
виде интерполяционных степенных уравнений вида:
Ср = a + bT + c'T −2
Ср = a + bT + cT2
– для неорганических веществ
– для органических веществ
H
T P
С учетом уравнения CP
для теплового эффекта реакции можно записать:
r H T
r CP (T )
T P
а также:
rU T
r CV (T )
T V
Эти уравнения называются
уравнениями Кирхгоффа в дифференциальной форме.
Лекции "Физическая химия, часть 1"
31

32.

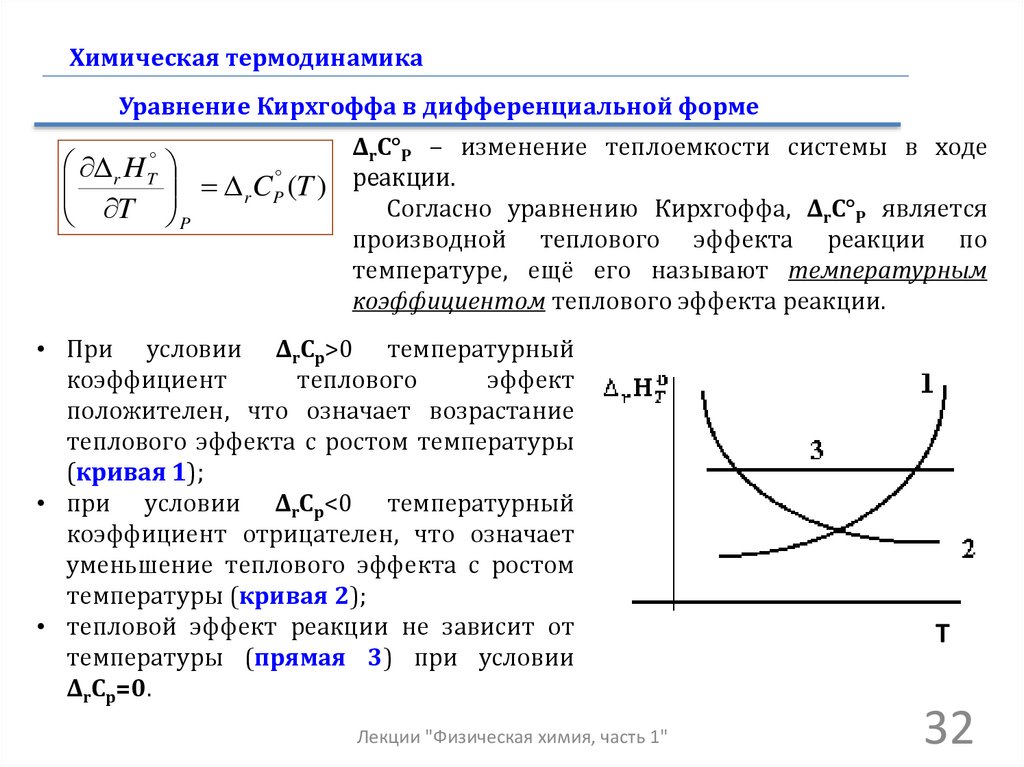
Химическая термодинамика
Уравнение Кирхгоффа в дифференциальной форме
ΔrC°P − изменение теплоемкости системы в ходе
r H
r CP (T ) реакции.
Согласно уравнению Кирхгоффа, ΔrC°P является
T P
производной теплового эффекта реакции по
температуре, ещё его называют температурным
коэффициентом теплового эффекта реакции.
T
• При условии ΔrCp>0 температурный
коэффициент
теплового
эффект
положителен, что означает возрастание
теплового эффекта с ростом температуры
(кривая 1);
• при условии ΔrCp<0 температурный
коэффициент отрицателен, что означает
уменьшение теплового эффекта с ростом
температуры (кривая 2);
• тепловой эффект реакции не зависит от
температуры (прямая 3) при условии
ΔrCp=0.
Лекции "Физическая химия, часть 1"
Т
32

33.

Химическая термодинамика
Уравнение Кирхгоффа в интегральной форме
Уравнение Кирхгоффа дает возможность вычислить тепловой эффект
при любой заданной температуре. Для этого уравнение необходимо
проинтегрировать.
Ввиду того, что при небольших давлениях тепловой эффект практически
не зависит от давления, частную производную можно заменить на полную
и разделить переменные:
dΔrHT0 = ΔrCpdT
После интегрирования получаем выражение для расчета теплового эффекта:
Уравнение Кирхгоффа
в интегральной форме
(здесь в качестве нижнего предела температуры взяли стандартную 298 К,
для которой легко вычислить тепловой эффект)
Лекции "Физическая химия, часть 1"
33

34.

Химическая термодинамика
Уравнение Кирхгоффа в интегральной форме
Если известны средние теплоемкости веществ (участников реакции) в
интервале температур от 298 К до Т, то получим выражение:
Для вычисления изменения средней теплоемкости необходимо
найти в справочных таблицах их средние значения:
Лекции "Физическая химия, часть 1"
34

35.

Химическая термодинамика
Уравнение Кирхгоффа в интегральной форме
Для более точного расчета теплового эффекта необходимо
использовать зависимости теплоемкостей веществ от температуры,
заданные в виде степенных уравнений (см. раньше):
T
r H r H
298
T
r a r bT r cT 2 r c T 2 dT
298
После интегрирования получим:
Лекции "Физическая химия, часть 1"
35

36.

Химическая термодинамика
Уравнение Кирхгоффа в интегральной форме
Имеется еще один способ расчета ΔrH°T,
с помощью высокотемпературной составляющей энтальпии:
r H T r H 298
r [ H T H 298
]
или
r H T r H 0 r [ H T H 0 ]
Высокотемпературные составляющей энтальпии [H°T−H°0] индивидуальных
веществ даны в справочнике.
ΔrH0 рассчитывается на основании имеющихся в справочнике величин ΔfH0.
Лекции "Физическая химия, часть 1"
36

37.

Химическая термодинамика
Второй закон термодинамики. Энтропия
Первый закон термодинамики, который мы рассмотрели перед этим,
позволяет составлять энергетические балансы термодинамических
процессов.
Но он не позволяет судить о возможности или невозможности того или
иного процесса.
Для этого используют второй закон термодинамики, который, так же,
как и первый закон, является постулатом, и применим для макросистем.
Лекции "Физическая химия, часть 1"
37

38.

Химическая термодинамика
Второй закон термодинамики. Энтропия
Имеются различные формулировки данного закона, которые являются
эквивалентными, либо следуют одна из другой.
Формулировка, предложенная Кельвином и Планком:
«Невозможна периодически действующая тепловая
машина, единственным результатом действия которой
было бы получение работы за счет отнятия теплоты от
теплового резервуара»
W = Q1 - Q2
Лекции "Физическая химия, часть 1"
38

39.

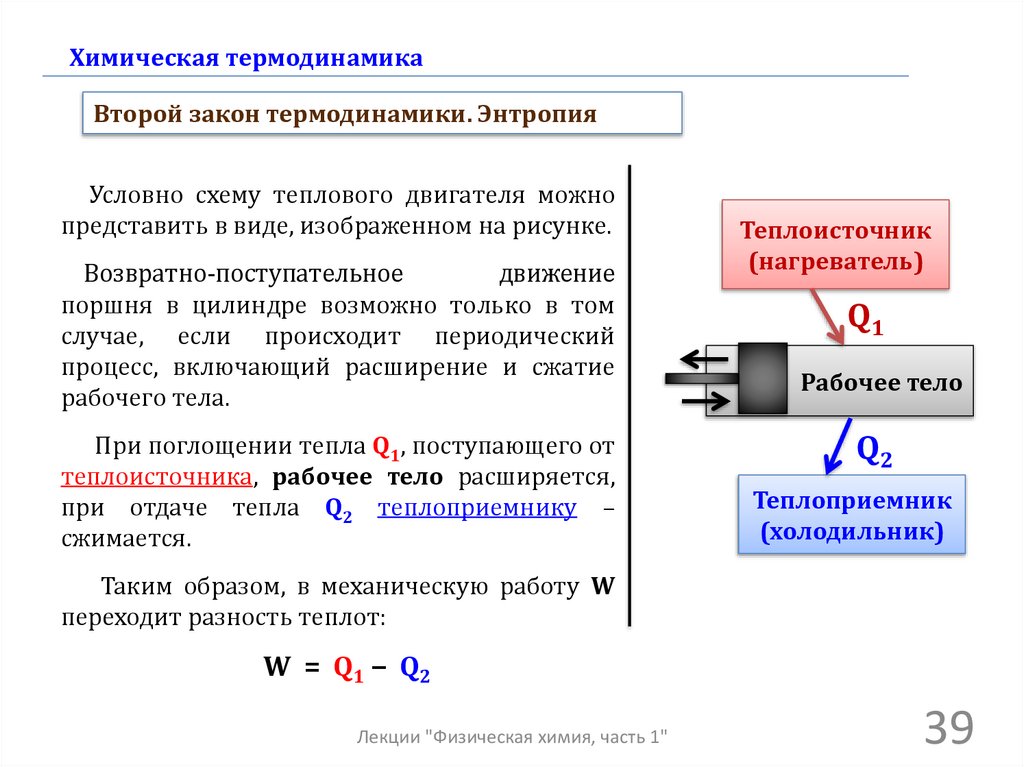
Химическая термодинамика
Второй закон термодинамики. Энтропия
Условно схему теплового двигателя можно
представить в виде, изображенном на рисунке.
Возвратно-поступательное
движение
поршня в цилиндре возможно только в том
случае, если происходит периодический
процесс, включающий расширение и сжатие
рабочего тела.
При поглощении тепла Q1, поступающего от
теплоисточника, рабочее тело расширяется,
при отдаче тепла Q2 теплоприемнику –
сжимается.
Теплоисточник
(нагреватель)
Q1
Рабочее тело
Q2
Теплоприемник
(холодильник)
Таким образом, в механическую работу W
переходит разность теплот:
W = Q1 − Q2
Лекции "Физическая химия, часть 1"
39

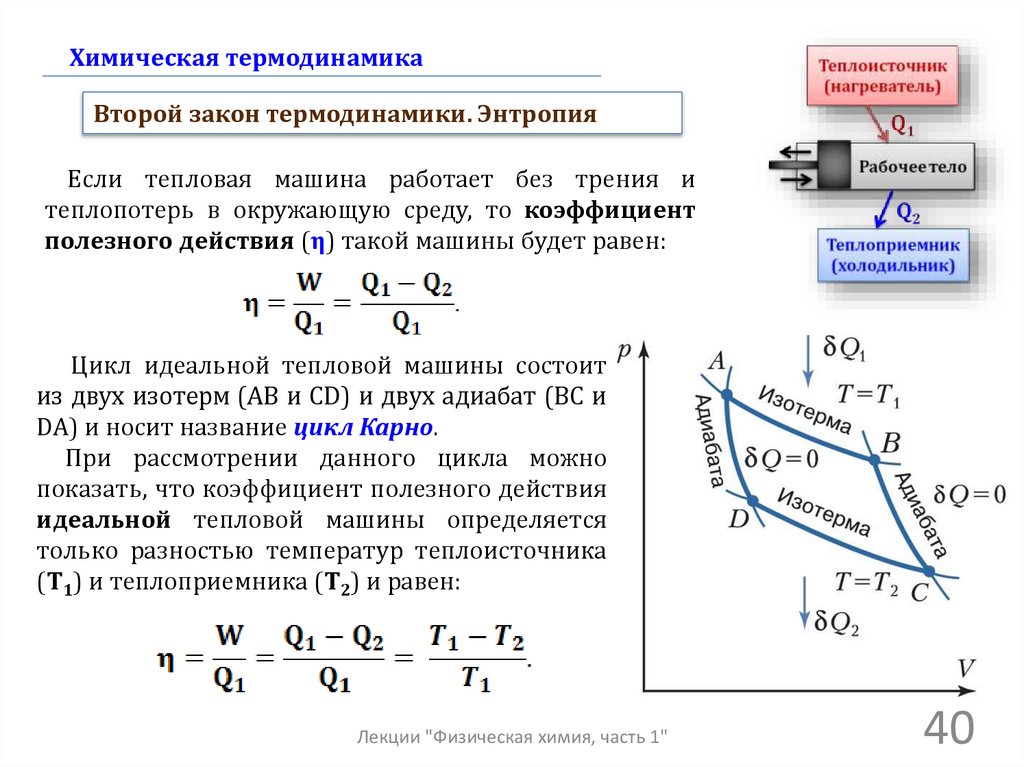
40.

Химическая термодинамика
Второй закон термодинамики. Энтропия
Если тепловая машина работает без трения и
теплопотерь в окружающую среду, то коэффициент
полезного действия (η) такой машины будет равен:
Цикл идеальной тепловой машины состоит
из двух изотерм (AB и CD) и двух адиабат (BC и
DA) и носит название цикл Карно.
При рассмотрении данного цикла можно
показать, что коэффициент полезного действия
идеальной тепловой машины определяется
только разностью температур теплоисточника
(Т1) и теплоприемника (Т2) и равен:
Лекции "Физическая химия, часть 1"
40

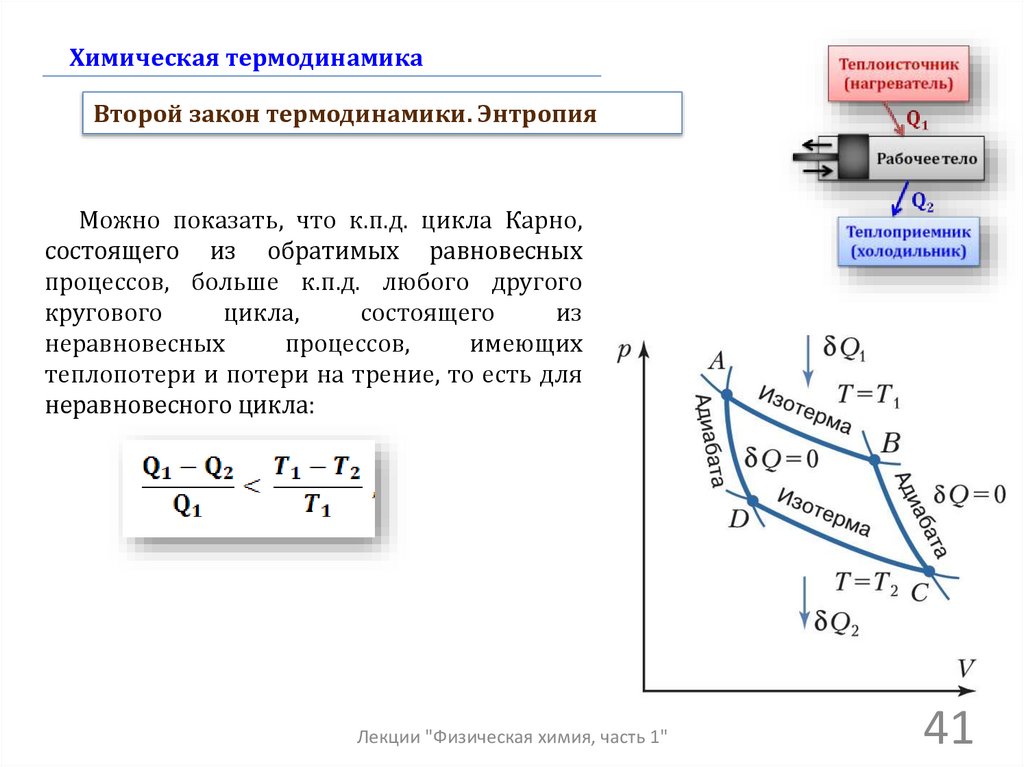
41.

Химическая термодинамика
Второй закон термодинамики. Энтропия
Можно показать, что к.п.д. цикла Карно,
состоящего из обратимых равновесных
процессов, больше к.п.д. любого другого
кругового
цикла,
состоящего
из
неравновесных
процессов,
имеющих
теплопотери и потери на трение, то есть для
неравновесного цикла:
Лекции "Физическая химия, часть 1"
41

42.

Химическая термодинамика
Второй закон термодинамики. Энтропия
Другие формулировки второго закона термодинамики:
Теплота не может самопроизвольно переходить от менее
нагретого тела к более нагретому
Невозможен вечный двигатель второго рода, т.е. такого
устройства, в котором всё подводимое тепло полностью
переходило бы в работу
Любая форма работы может полностью перейти в теплоту, но
теплота преобразуется в работу лишь частично.
Лекции "Физическая химия, часть 1"
42

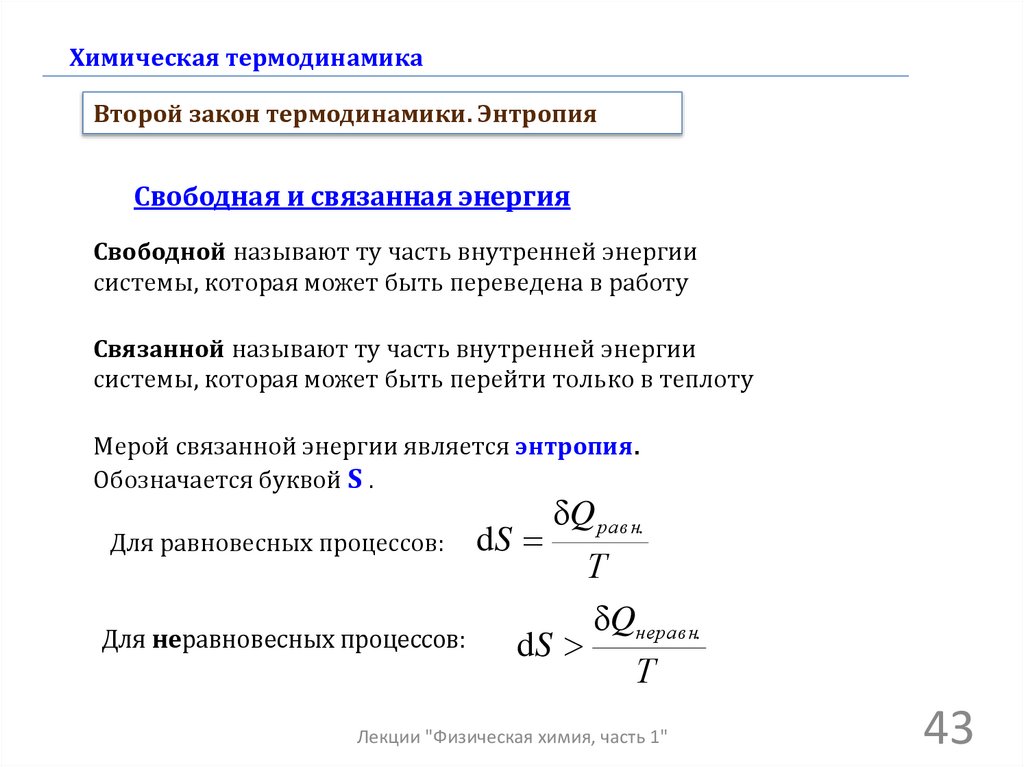
43.

Химическая термодинамика
Второй закон термодинамики. Энтропия
Свободная и связанная энергия
Свободной называют ту часть внутренней энергии
системы, которая может быть переведена в работу
Связанной называют ту часть внутренней энергии
системы, которая может быть перейти только в теплоту
Мерой связанной энергии является энтропия.
Обозначается буквой S .
Для равновесных процессов:
Для неравновесных процессов:
dS
δQ равн.
dS
Т
δQнеравн.
Т
Лекции "Физическая химия, часть 1"
43

44.

Химическая термодинамика
Второй закон термодинамики. Энтропия
dS
δQнеравн.
Т
Это уравнение является математической записью
второго закона термодинамики для неравновесных
процессов
Если неравновесный процесс протекает в изолированной системе, то
δQ = 0, U = const, V = const, и из уравнения следует, что
(dS)U,V > 0 или (ΔS)U,V > 0
Когда в результате неравновесного процесса изолированная система
придет в состояние равновесия, то энтропия ее достигнет максимума, и
условиями равновесия будут:
(dS)U,V = 0;
(d2 S)U,V = 0;
(ΔS)U,V = 0
Таким образом, изменение энтропии может служить критерием
направленности и равновесия термодинамических процессов в
изолированной системе.
Лекции "Физическая химия, часть 1"
44

45.

Химическая термодинамика
Изменение энтропии в различных процессах
Рассмотрим вычисление изменения энтропии для ряда обратимых
процессов.
1.Изменение энтропии при фазовых переходах.
Фазовые равновесные превращения первого рода – переходы одной
кристаллической модификации вещества в другую, плавление, возгонка,
испарение протекают при постоянных давлении и температуре.
dS
δQ равн.
Т
Итак, при фазовом переходе:
Лекции "Физическая химия, часть 1"
45

46.

Химическая термодинамика
Изменение энтропии в различных процессах
2. Изменение энтропии при нагревании (охлаждении) системы
При изохорном процессе
При изобарном процессе
Если полагать, что теплоемкость не зависит от температуры, то:
При V=const
При Р=const
При нагревании энтропия всегда увеличивается!
Лекции "Физическая химия, часть 1"
46

47.

Химическая термодинамика
Изменение энтропии в различных процессах
3. Изменение энтропии для различных процессов с идеальным газом
Выразим δQр из уравнения
dS
δQ равн.
Т
и подставим в выражение:
получим:
объединенное выражение
первого и второго законов
термодинамики
Лекции "Физическая химия, часть 1"
47

48.

Химическая термодинамика
Изменение энтропии в различных процессах
3. Изменение энтропии для различных процессов с идеальным газом
Выразим δQр из уравнения
dS
δQ равн.
Т
и подставим в выражение:
получим:
При Т=const:
ΔS R ln
или
Лекции "Физическая химия, часть 1"
V2
P
R ln 1
V1
P2
48

49.

Химическая термодинамика
Изменение энтропии в различных процессах
4. Изменение энтропии при смешении идеальных газов
Δсм еш. S n1 R ln
V1 V2
V V
n2 R ln 1 2
V1
V2
где:
n1 и n2 – число молей газов,
V1 и V2 – начальные объемы газов
Лекции "Физическая химия, часть 1"
49

50.

Химическая термодинамика
Изменение энтропии в различных процессах
5. Изменение энтропии при протекании химической реакции
Если реакция совершает один пробег при постоянных температуре и
давлении, то изменение энтропии:
где ν – стехиометрические коэффициенты, S – мольные энтропии реагентов,
значения которых можно найти в таблицах для стандартных условий.
Для произвольно выбранной температуры Т и постоянном давлении:
Лекции "Физическая химия, часть 1"
50

51.

Химическая термодинамика
Статистическое толкование понятия энтропия
Формулировка Планка соответствует определению энтропии в
статистической физике через термодинамическую вероятность состояния
системы:
S k ln
Где k= 1,38∙10−23 Дж/К − постоянная Больцмана,
Ω − термодинамическая вероятность состояния системы
Лекции "Физическая химия, часть 1"
51

52.

Химическая термодинамика
Третий закон
термодинамики
По приведенным выше уравнениям можно вычислять лишь изменение
энтропии (ΔS) в различных процессах, но найти абсолютное значение
энтропии (S) не представляется возможным.
В. Нернст в 1906 году пришел к выводу, что вблизи абсолютного нуля
температур изменение энтропии становится пренебрежимо малым.
Позднее М. Планк в 1912 году высказал утверждение, не доказуемое на
опыте, что при абсолютном нуле энтропия чистого кристаллического
вещества равна нулю.
Это утверждение получило название постулата Планка или третьего
закона термодинамики и позволило предложить способ вычисления
абсолютного значения энтропии для различных веществ.
Лекции "Физическая химия, часть 1"
52

53.

Химическая термодинамика
Третий закон термодинамики
Рассчитаем абсолютную энтропию 1 моль идеального газа при
температуре Т:
Нагрев
твердого
от 0 К до Тпл.
Плавление
при Тпл.
lim [