Разбор некоторых задач по БП и ДП (простой вариант ДП – мемоизация)

1.

Разбор некоторых задач по БП и ДП
(простой вариант ДП – мемоизация)
Разбираем задачки…

2.

1 Префиксные суммы. 1.1 Задача из Квалификации - 2023

3.

1 Префиксные суммы. 1.1 Задача из Квалификации - 2023

4.

1 Префиксные суммы. 1.1 Задача из Квалификации - 2023
Объемы входных данных и ограничения по времени говорят о том, что эту задачу нельзя
решить перебором ! O(n^2) при n = 2 * 10 ^ 5 даст 4 * 10 ^ 10 - нельзя посчитать за 1 с !
Идея – используем префиксные суммы . Мы считаем префиксные суммы для всех четных
номеров карточек и для всех нечетных номеров карточек, затем перебираем все карточки и
для каждой карточки по массиву префиксных сумм определяем, чему будет равна сумма ДО
этой карточки для четных (Монокарп ходит первым с шага 0 – тогда четных, либо 1 – тогда
нечетных) + сумма ПОСЛЕ этой карточки, но уже для суммы другой четности. И находим
максимум из этих значений.

5.

1 Префиксные суммы. 1.2 Задача из Лиги Поволжья и Юга – 24
(Div 2 раунд 3)

6.

1 Префиксные суммы. 1.2 Задача из Лиги Поволжья и Юга – 24
(Div 2 раунд 3)

7.

1 Префиксные суммы. 1.2 Задача из Лиги Поволжья и Юга – 24
(Div 2 раунд 3)
Объемы входных данных и ограничения по времени, а точнее – необходимость выполнять
множество запросов на строке из n = 3 * 10 ^ 5 символов - нельзя посчитать за 2 с !
Идея – используем массив префиксных сумм количества подряд идущих символов.

8.

1 Префиксные суммы. 1.3 Задача D из Round 859 (Div. 4)

9.

1 Префиксные суммы. 1.3 Задача D из Round 859 (Div. 4)

10.

1 Префиксные суммы. 1.3 Задача D из Round 859 (Div. 4)
Объемы входных данных и ограничения по времени говорят о том, что эту задачу нельзя
решить перебором ! O(n^2) при n = 2 * 10 ^ 5 даст 4 * 10 ^ 10.
Идея – используем префиксные суммы . То есть мы считаем префиксные суммы,
соответственно, для любых l и r мы сможем найти за O(1) нужные подсуммы. Нужно обратить
внимание на возможные переполнения (не на питоне !), а на С++ нужно использовать тип
long long. Как вариант – можно использовать не сами суммы, а их четность / нечетность, что
сильно сэкономит память и немного – время.

11.

1 Префиксные суммы. 1.4 Задача B из Round 836 (Div. 2)

12.

1 Префиксные суммы. 1.4 Задача B из Round 836 (Div. 2)

13.

1 Префиксные суммы. 1.4 Задача B из Round 836 (Div. 2)
Объемы входных данных и ограничения по времени говорят о том, что эту задачу нельзя
решить перебором ! n и k <= 2 * 10 ^ 5
Идея – используем префиксную сумму (без массива таких сумм) . Перебираем элементы
массива и считаем максимальную сумму префикса.

14.

1 Динамика (?). 1.5 Задача D из Round 937 (Div. 4)

15.

1 Динамика (?). 1.5 Задача D из Round 937 (Div. 4)

16.

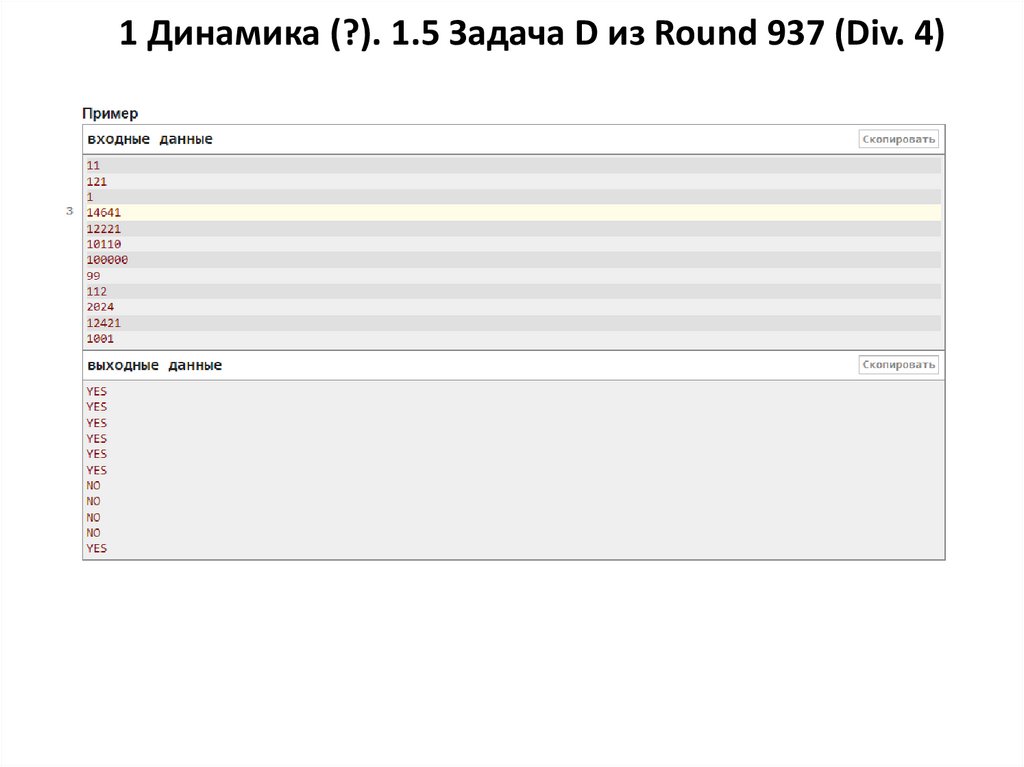
1 Динамика (?). 1.5 Задача D из Round 937 (Div. 4)
Объемы входных данных и ограничения по времени говорят о том, что эту задачу нельзя
решить перебором ! Числа до 10^5 и кол-во тестов = 50 000 !
Идея – используем мемоизацию (не обязательно) и аналог метода разложения числа на
простые множители. Можно ли упростить код ниже ?