Similar presentations:
Нелинейные структуры данных. Графы
1. Нелинейные структуры данных. Графы
12. Леонард Эйлер
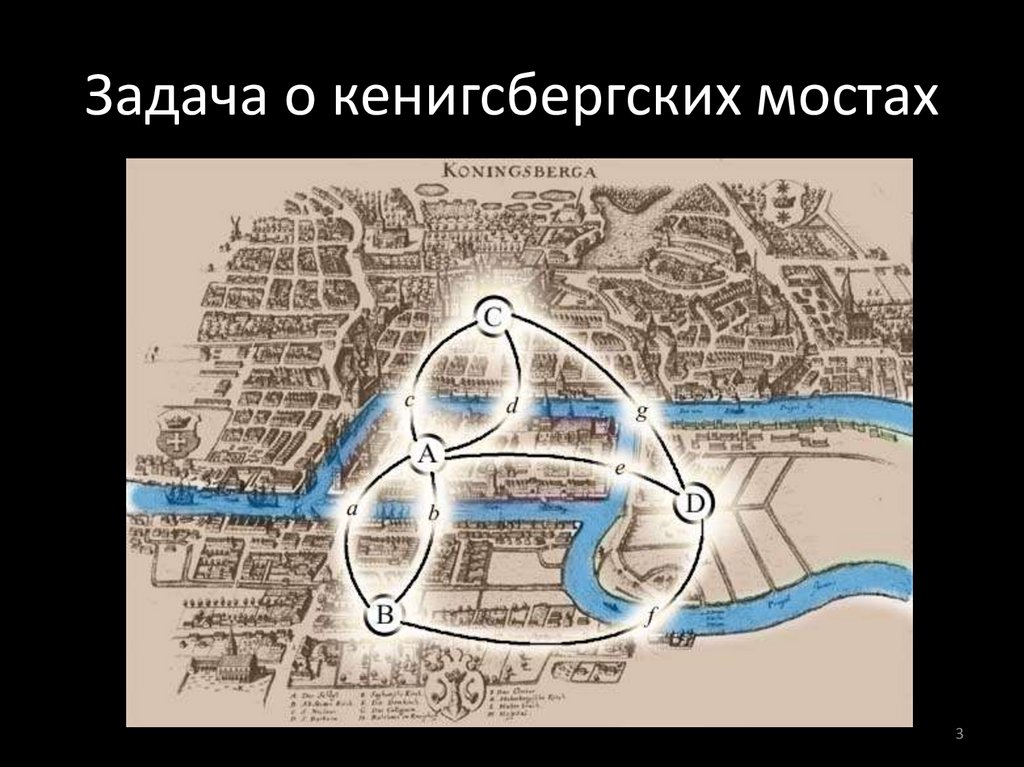
23. Задача о кенигсбергских мостах
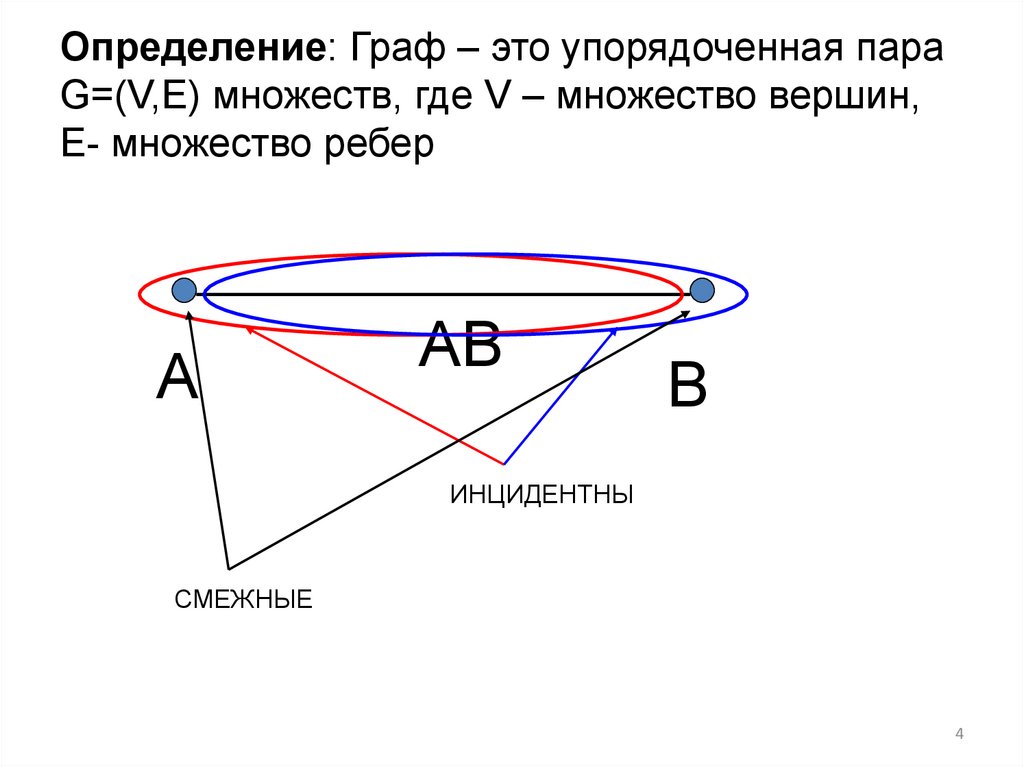
34. Определение: Граф – это упорядоченная пара G=(V,E) множеств, где V – множество вершин, E- множество ребер
AAB
B
ИНЦИДЕНТНЫ
СМЕЖНЫЕ
4
5.
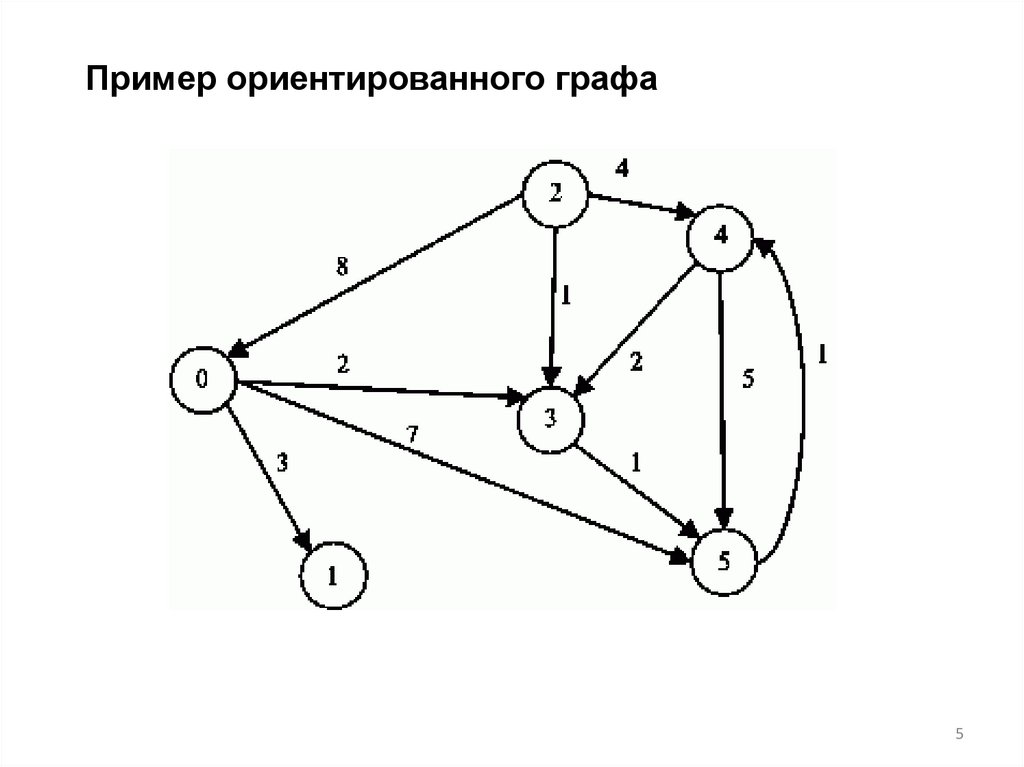
Пример ориентированного графа5
6.
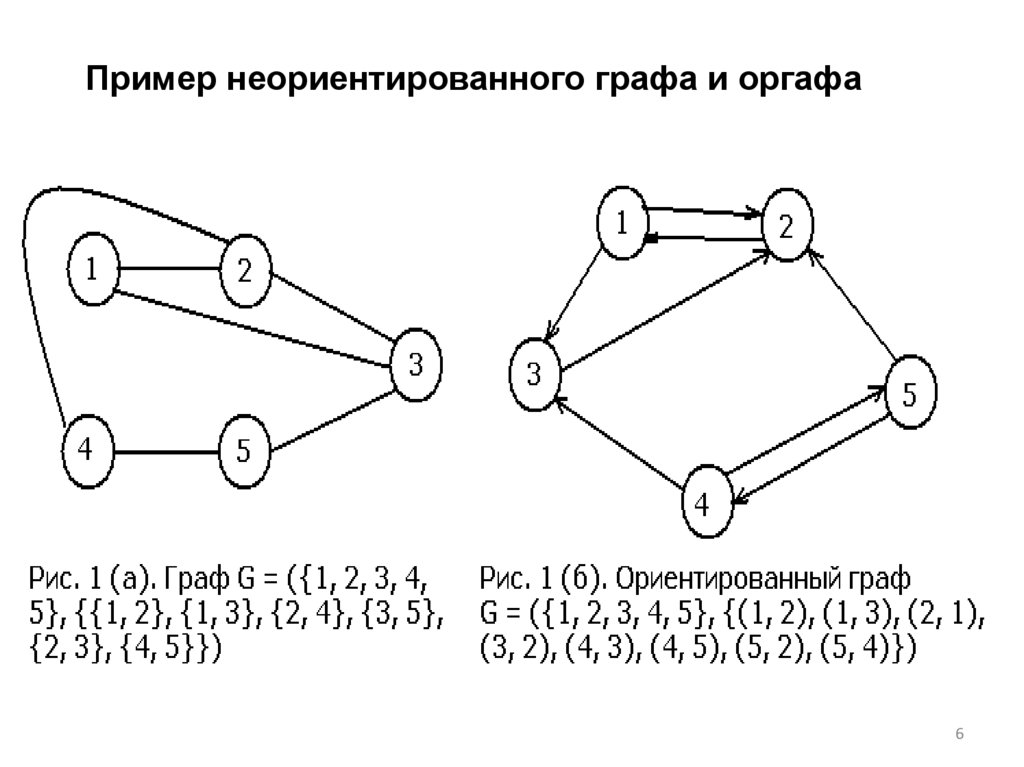
Пример неориентированного графа и оргафа6
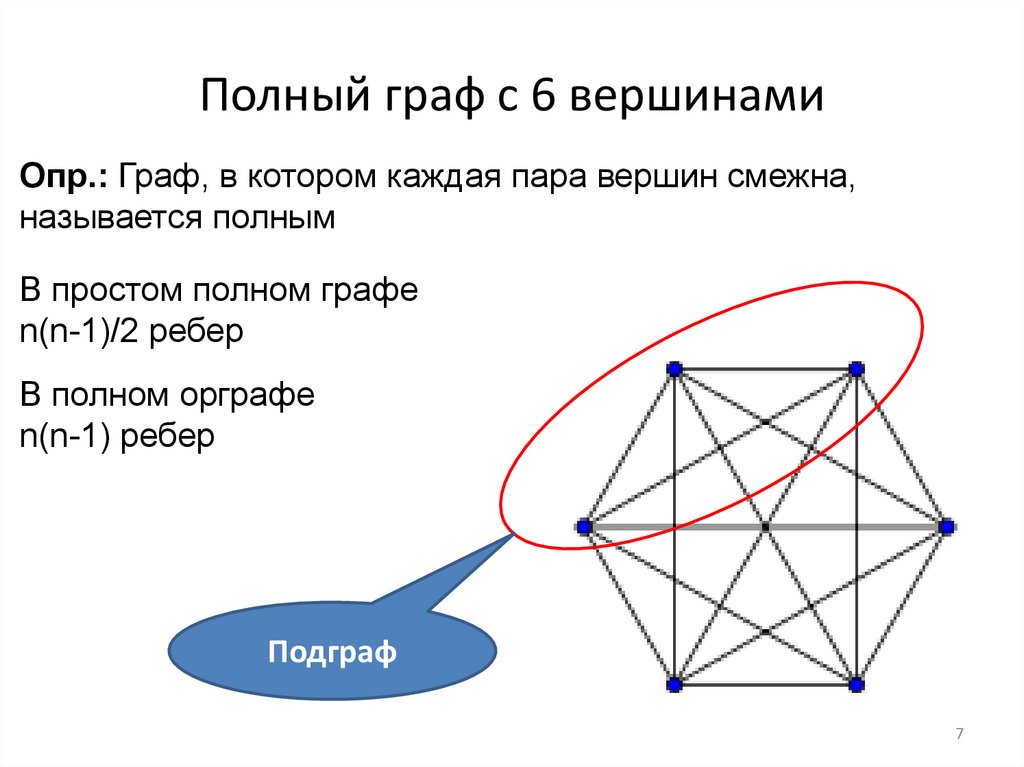
7. Полный граф с 6 вершинами
Опр.: Граф, в котором каждая пара вершин смежна,называется полным
В простом полном графе
n(n-1)/2 ребер
В полном орграфе
n(n-1) ребер
Подграф
7
8.
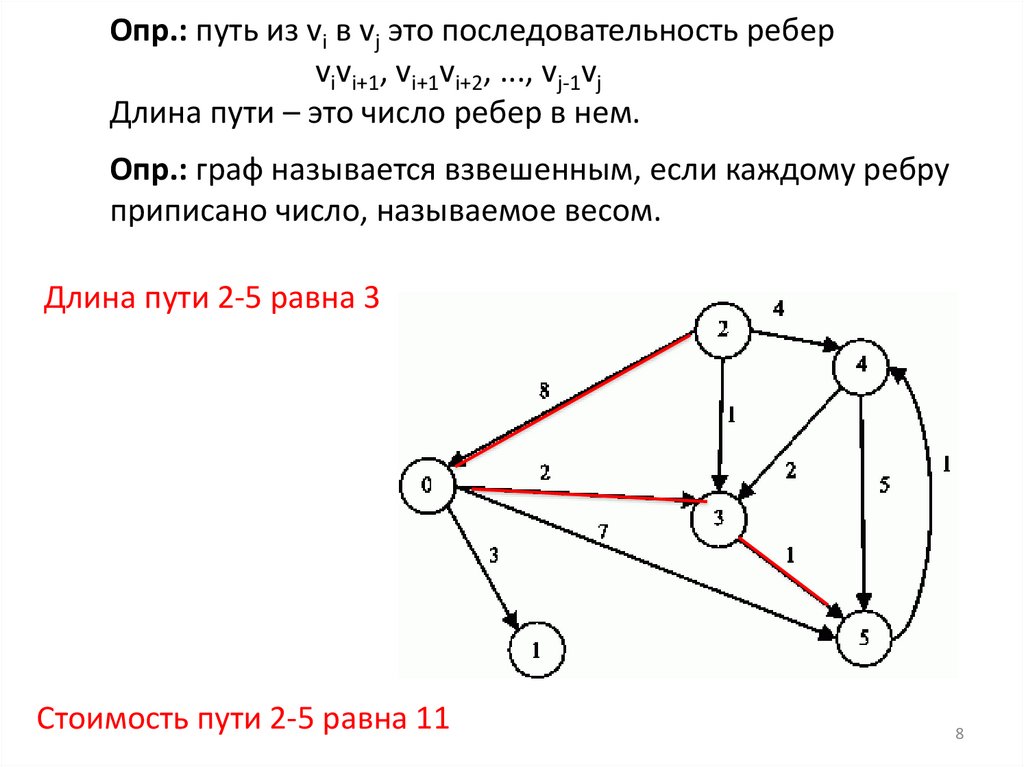
Опр.: путь из vi в vj это последовательность реберvivi+1, vi+1vi+2, ..., vj-1vj
Длина пути – это число ребер в нем.
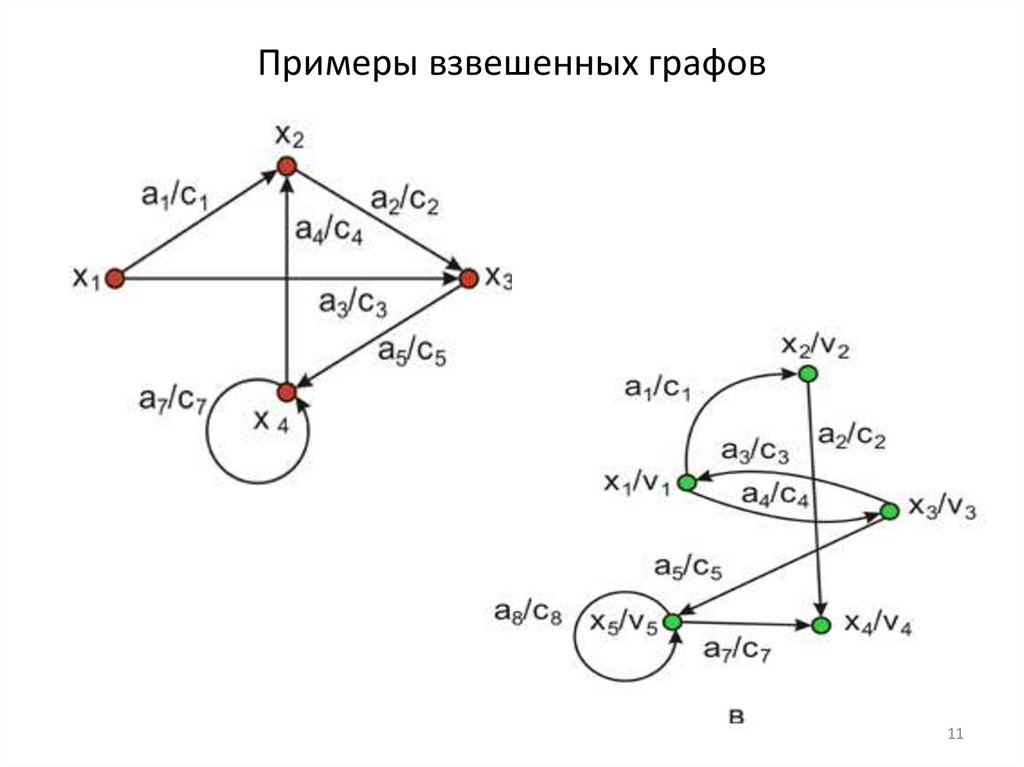
Опр.: граф называется взвешенным, если каждому ребру
приписано число, называемое весом.
Длина пути 2-5 равна 3
Стоимость пути 2-5 равна 11
8
9.
Опр.: граф называется связным, если всякую пару вершинможно соединить по крайней мере одним путем.
Опр.: Цикл – это путь, который начинается и заканчивается
в одной и той же вершине.
Опр.: Дерево – это связный ациклический граф .
9
10.
1011. Примеры взвешенных графов
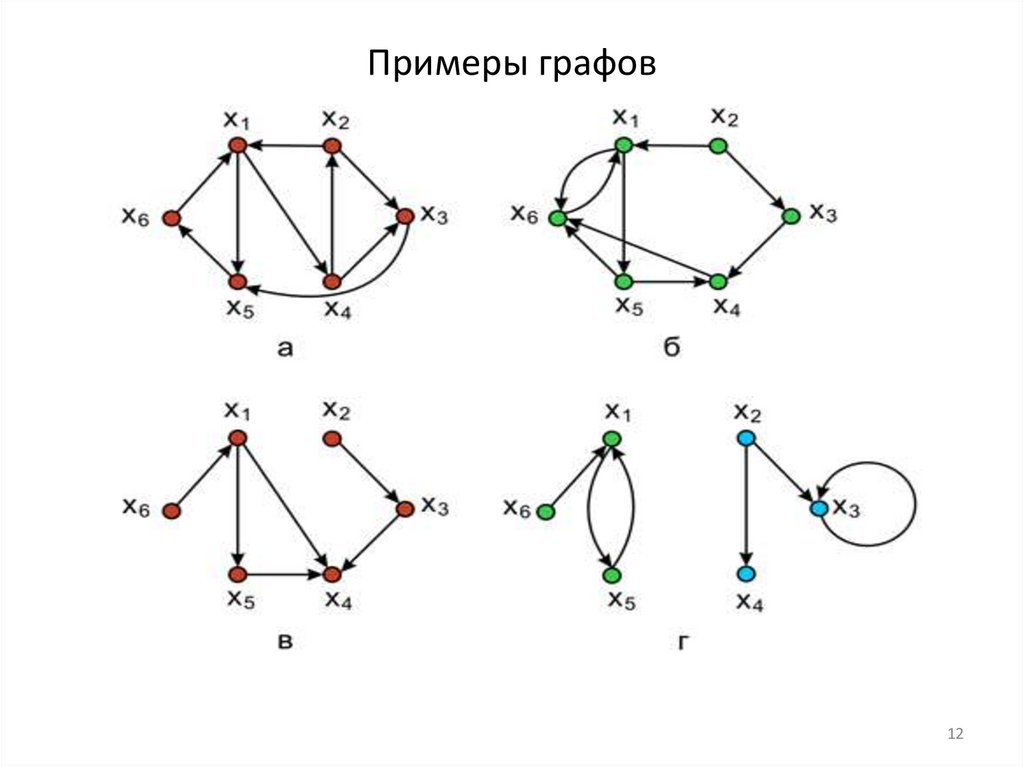
1112. Примеры графов
1213.
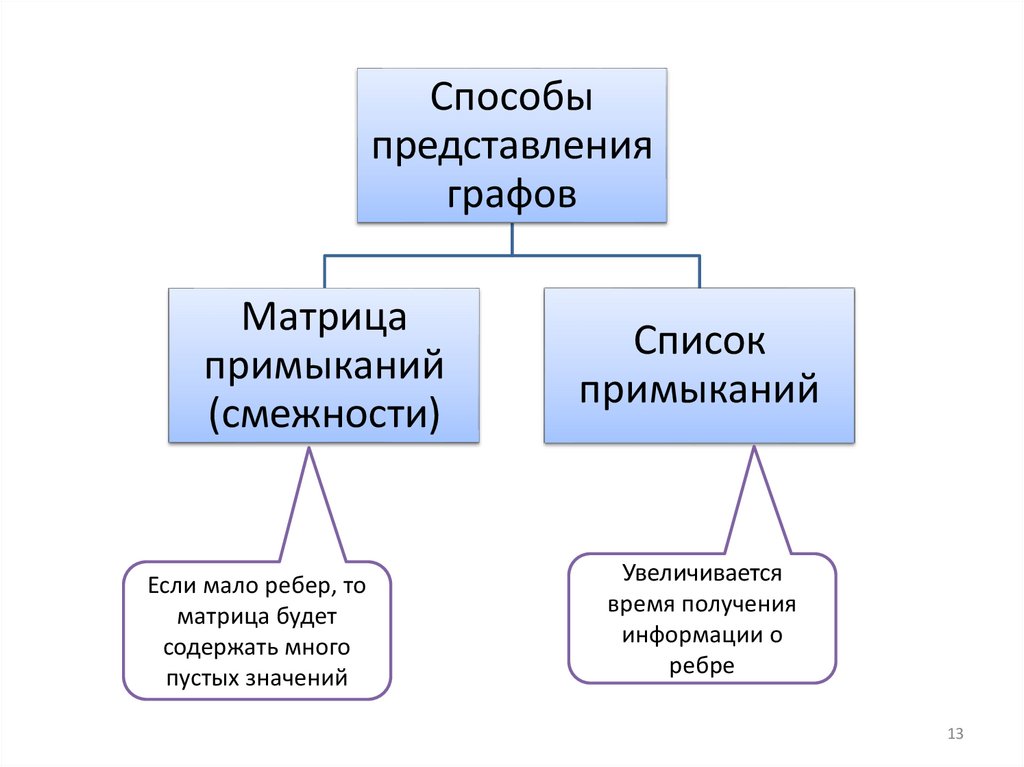
Способыпредставления
графов
Матрица
примыканий
(смежности)
Если мало ребер, то
матрица будет
содержать много
пустых значений
Список
примыканий
Увеличивается
время получения
информации о
ребре
13
14. Структуры данных для представления графов
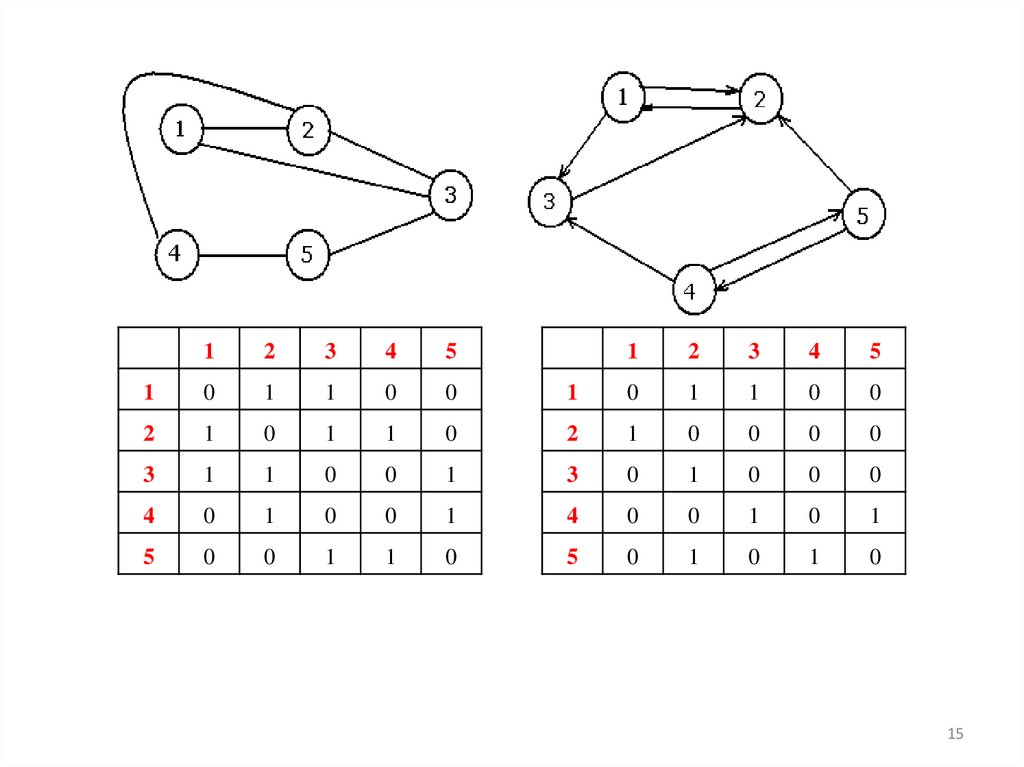
1. Матрица примыканий графа G=(V,E)14
15.
12
3
4
5
1
2
3
4
5
1
0
1
1
0
0
1
0
1
1
0
0
2
1
0
1
1
0
2
1
0
0
0
0
3
1
1
0
0
1
3
0
1
0
0
0
4
0
1
0
0
1
4
0
0
1
0
1
5
0
0
1
1
0
5
0
1
0
1
0
15
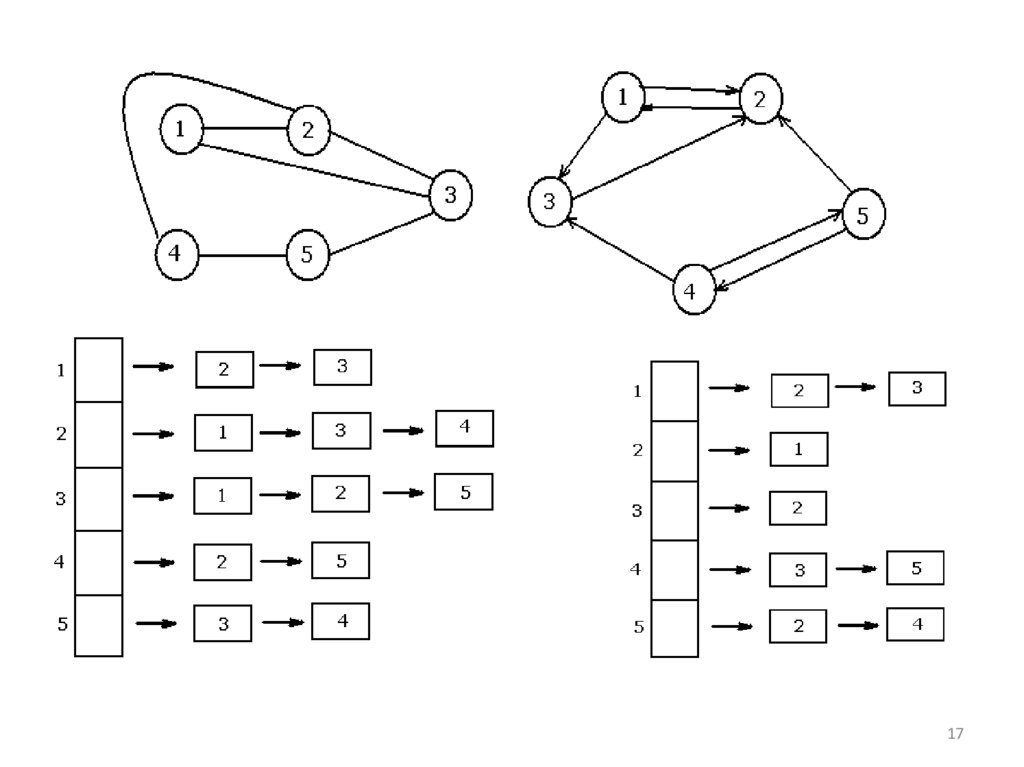
16. Структуры данных для представления графов
2. Список примыканий графа G=(V,E) с числомвершин n записывается в виде одномерного
массива длины n, каждый элемент которого
представляет собой ссылку на список вершин,
смежных с соответствующей вершиной графа
16
17.
1718.
Обходыграфов
В глубину
Идем настолько
глубоко по графу,
насколько это
возможно
В ширину
Двигаемся
равномерно вдоль
всех возможных
направлений
18
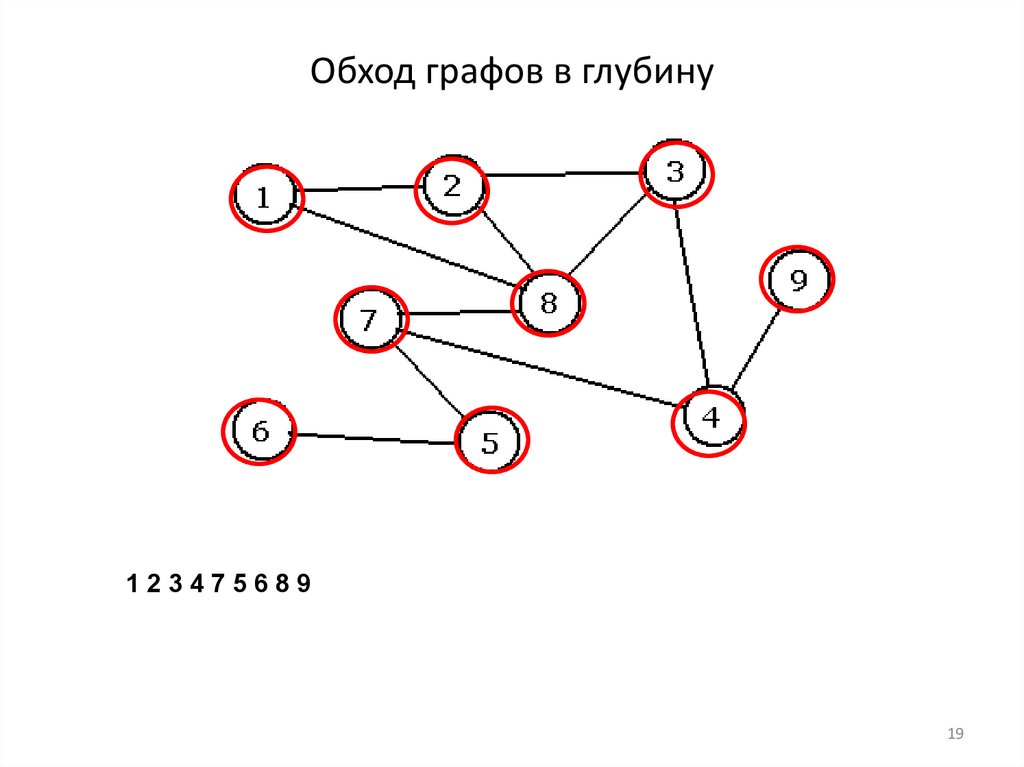
19. Обход графов в глубину
12347568919
20. Рекурсивный алгоритм обхода в глубину
DepthFirstTraversal (G, v)G граф
v текущий узел
Visit(v)
Mark(v)
for каждого ребра vw графа G do
if вершина w непомечена then
DepthFirstTraversal(G, w)
end if
end for
20
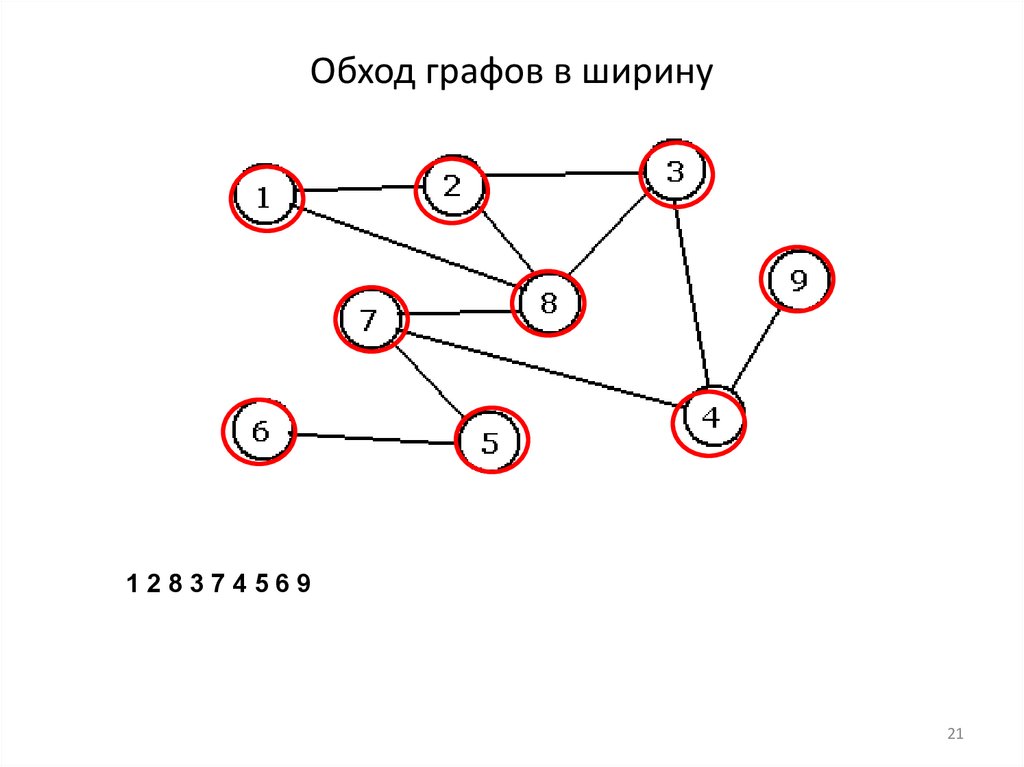
21. Обход графов в ширину
12837456921
22. Рекурсивный алгоритм обхода в ширину
BreadthFirstTraversal(G, v)G граф
v текущий узел
Visit(v)
Mark(v)
Enqueue(v)
while очередь непуста do
Dequeue(v)
for каждого ребра vw в графе G do
if вершина w непомечена then
Visit(w)
Mark(w)
Enqueue(w)
end if
end for
end while
22
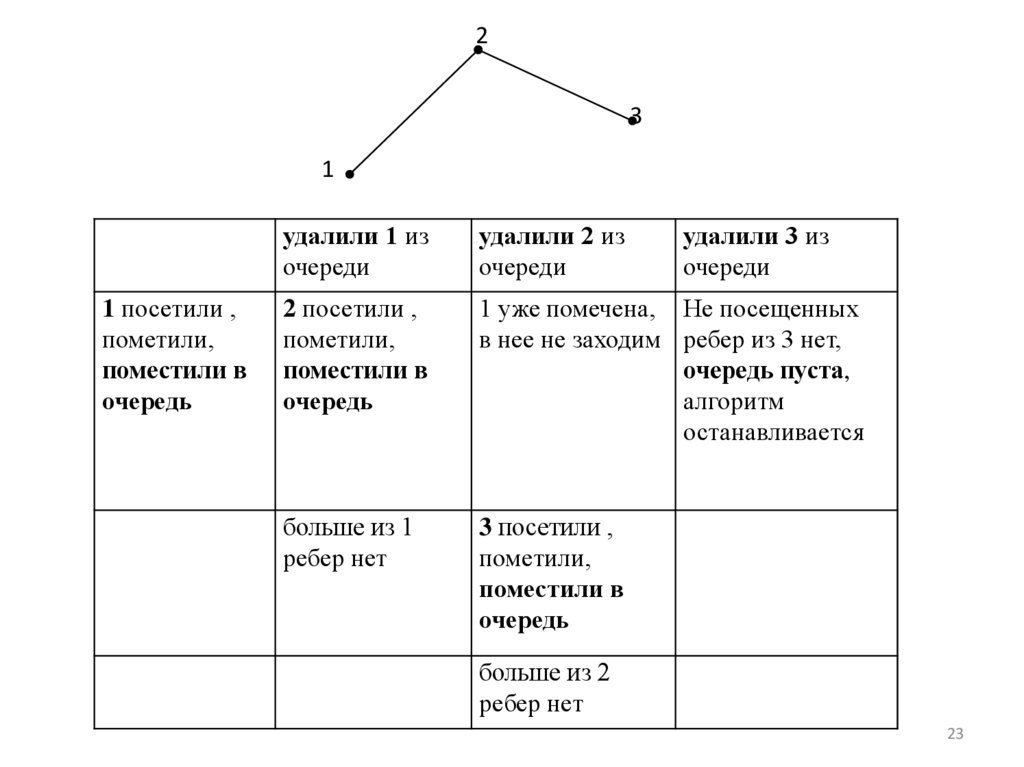
23.
23
1
1 посетили ,
пометили,
поместили в
очередь
удалили 1 из
очереди
удалили 2 из
очереди
удалили 3 из
очереди
2 посетили ,
пометили,
поместили в
очередь
1 уже помечена, Не посещенных
в нее не заходим ребер из 3 нет,
очередь пуста,
алгоритм
останавливается
больше из 1
ребер нет
3 посетили ,
пометили,
поместили в
очередь
больше из 2
ребер нет
23
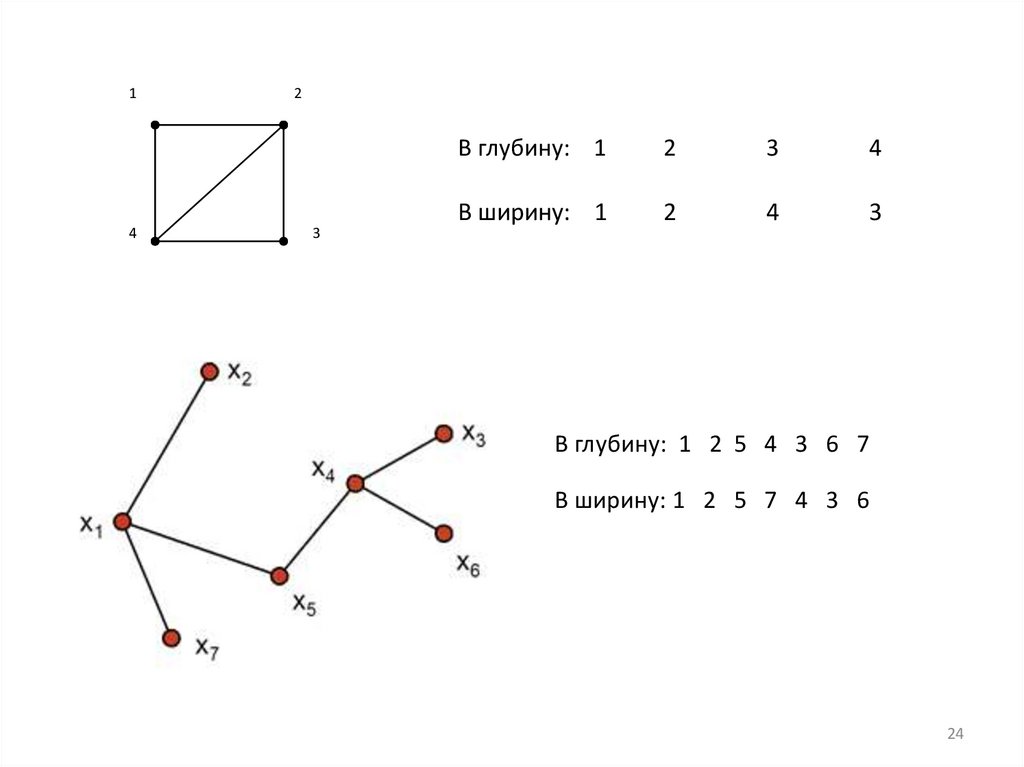
24.
14
2
3
В глубину: 1
2
3
4
В ширину: 1
2
4
3
В глубину: 1 2 5 4 3 6 7
В ширину: 1 2 5 7 4 3 6
24
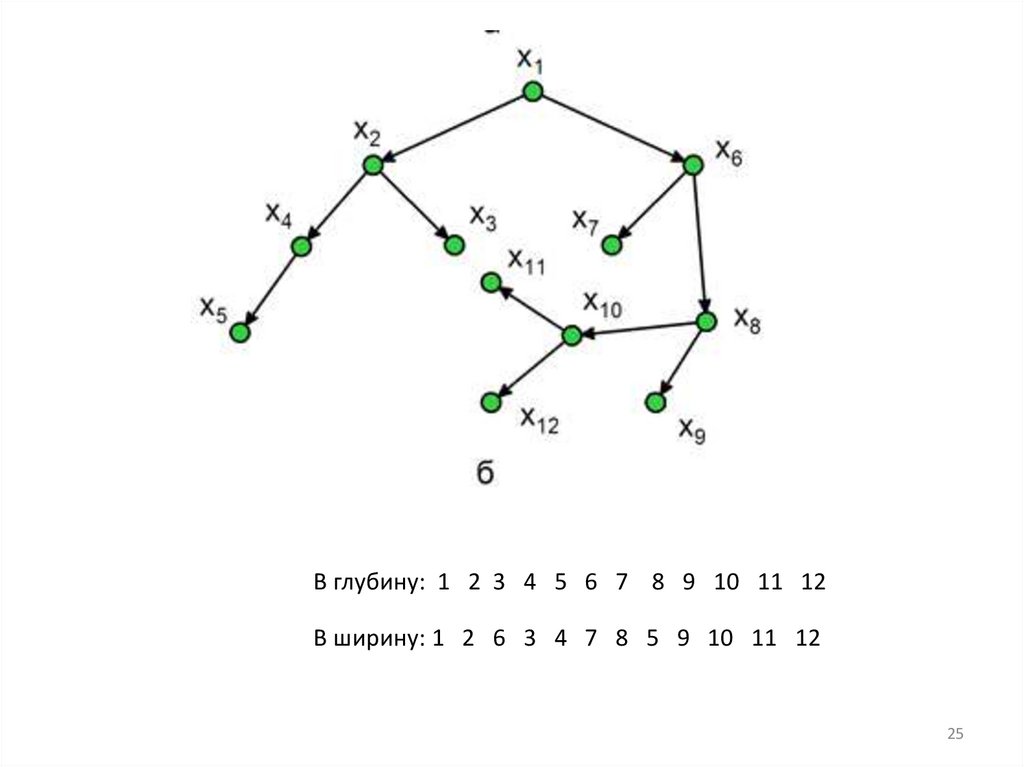
25.
В глубину: 1 2 3 4 5 6 7 8 9 10 11 12В ширину: 1 2 6 3 4 7 8 5 9 10 11 12
25
26.
• https://reference.wolfram.com/language/Combinatorica/guide/GraphAlgorithms.html
26








 mathematics
mathematics








