Элементы комбинаторики

1.

2.

Произведение натуральных чисел от 1
до n в математике называют
факториалом числа n и обозначают n!
Символ n! от латинского factor, что
значит множитель.
0!=1, 3!=1·2·3=6.
При n=1 n!=1!=1

3.

Перестановкой из n элементов называется
всякое расположение элементов данного
конечного множества, получающееся при
некотором упорядочении этого множества,
причем отдельные подмножества различаются
только порядком своих элементов. Число
перестановок из n элементов равно произведению
первых n натуральных чисел
24.05.24
3

4.

Задача: Сколькими способами можно разместить
группу учеников 8 «А» класса, изучающих немецкий
язык, если их количество 10 человек, а аудитория
(кабинет) содержит 10 посадочных мест?
Решение: Число способов равно
Р10=10!=10·9·8·7·6·5·4·3·2·1=3628800.
24.05.24
4

5.

Размещением из n элементов по m в каждом ( )
называется любое упорядоченное подмножество из m
элементов множества, состоящего из n различных
элементов.
24.05.24
5

6.

Задача: В президиум собрания избраны 8
человек. Сколькими способами они могут
распределить между собой обязанности
председателя, секретаря и счётчика (если нет
компьютера)?
Решение: Искомое число есть размещение
из 8 элементов по 3:
24.05.24
6

7.

.
Сочетанием из n элементов по m
называется любое подмножество из m
элементов, которые принадлежат множеству,
состоящему из n различных элементов.
Сочетания(комбинации)
Число сочетаний вычисляется по формуле
24.05.24
7

8.

.
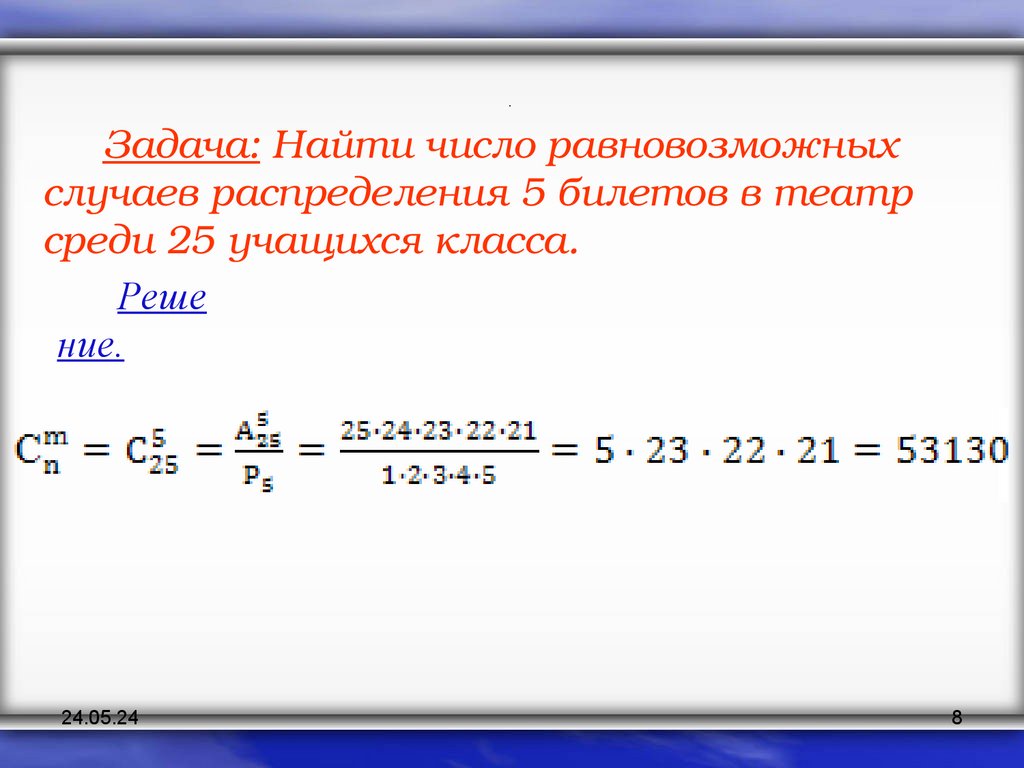
Задача: Найти число равновозможных
случаев распределения 5 билетов в театр
среди 25 учащихся класса.
Реше
ние.
24.05.24
8

9.

24.05.24
9

10.

.
Число размещений из n элементов по k с
повторениями вычисляем по формуле
24.05.24
10

11.

Задача: В гостинице 10 комнат, каждая из
которых может разместить 4 человека.
Сколько существует вариантов размещения 4
гостей?
Решение. Каждый гость может быть
размещён в одну из 10 комнат.
24.05.24
11

12. Анализ самостоятельной работы предыдущего урока

13.

Вариант I
Вариант II
1. Лена сказала своей
1. Чтобы приобрести 8
подруге, что для
тетрадей по математике ( в
покупки обеда, мама
клетку) мама дала Серёже
дала ей ________руб.
_________руб. Сколько
Сколько денег дала мама стоит 1 тетрадь, если все
Лене?
деньги были
Ответ: 7,5 р.
израсходованы.
Ответ: 2,5 руб.
24.05.24
13

14.

Вариант I
Вариант II
1. Число перестановок из n 1. В конференции
букв относится к числу
участвовало 25 человек.
перестановок из n+2 букв, Каждый с каждым
как 0,1 к 3. Найти n.
обменялись визитной
(Решение.
карточкой. Сколько всего
понадобиться карточек?
(25·24=600).
Следует (n+1)(n+2)=30
n1=4, n=-7
n___N, значит, n=4.)
24.05.24
14

15.

Вариант I
3. У меня есть 9 разных
книг из серии
«Занимательная
математика».
Сколькими способами я
могу выбрать 3 из них
победителю школьной
математической
олимпиады?
Вариант II
3. Число сочетаний из n
элементов по 3 в 5 раз
меньше числа сочетаний
из (n+2) элементов по 4.
Найти n.
n=3 или n=14
24.05.24
15

16.

4. Составить задачу практической
направленности по данным школьной жизни.
24.05.24
16

17.

Теория вероятностей –
математическая наука,
позволяющая по вероятностям
одних случайных событий
находить вероятности других
случайных событий, связанных
каким – либо образом с
первыми.
24.05.24
17

18.

Определение 1. Два события называются
несовместными, если они в рассматриваемом опыте не
могут произойти одновременно.
Определение 2. События, которые в рассматриваемом
опыте могут произойти одновременно, называются
совместными.
Определение 3. Событие А благоприятствует событию
В, если из того, что произошло событие А следует, что
произошло событие В.
24.05.24
18

19. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

24.05.24
19

20.

КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.
Вероятностью Р наступления
случайного события А называется
отношение
m
n,
где n – число всех
возможных исходов эксперимента, а m –
число всех благоприятных исходов:
m
P ( A)
n
24.05.24
20

21.

Классическое
определение
вероятности было
впервые дано в
работах
французского
математика Лапласа.
Пьер-Симо́н Лапла́с
24.05.24
21

22.

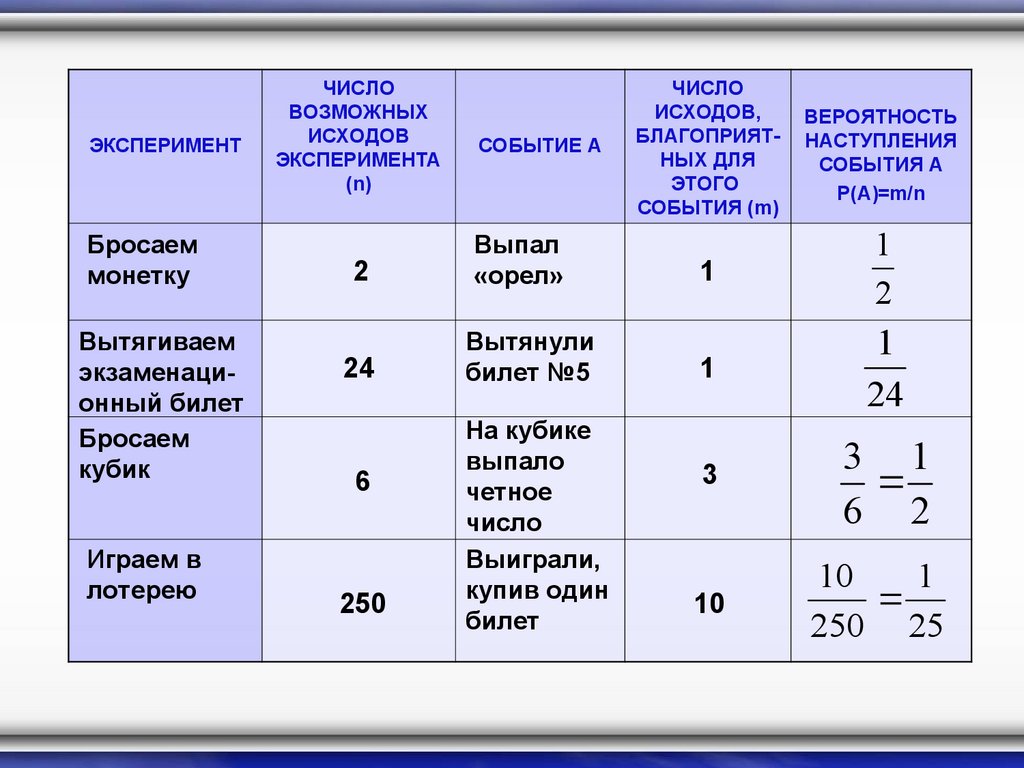
ЭКСПЕРИМЕНТ
Бросаем
монетку
Вытягиваем
экзаменационный билет
Бросаем
кубик
Играем в
лотерею
ЧИСЛО
ВОЗМОЖНЫХ
ИСХОДОВ
ЭКСПЕРИМЕНТА
(n)
2
24
6
250
СОБЫТИЕ А
Выпал
«орел»
Вытянули
билет №5
На кубике
выпало
четное
число
Выиграли,
купив один
билет
ЧИСЛО
ИСХОДОВ,
БЛАГОПРИЯТНЫХ ДЛЯ
ЭТОГО
СОБЫТИЯ (m)
ВЕРОЯТНОСТЬ
НАСТУПЛЕНИЯ
СОБЫТИЯ А
Р(А)=m/n
1
1
2
1
1
24
3
3 1
6 2
10
10
1
250 25