Similar presentations:
Тригонометрическая и показательная форма комплексного числа
1.
Министерство образования и науки Нижегородской областиГосударственное бюджетное профессиональное образовательное учреждение
«Уренский индустриально-энергетический техникум»
ТРИГОНОМЕТРИЧЕСКАЯ И
ПОКАЗАТЕЛЬНАЯ ФОРМА
КОМПЛЕКСНОГО ЧИСЛА
Разработал:
преподаватель ЕН.01 Математика
Соловьев А.А.
г. Урень, 2024 г.
2.
Министерство образования и науки Нижегородской областиГосударственное бюджетное профессиональное образовательное учреждение
«Уренский индустриально-энергетический техникум»
ОПРЕДЕЛЕНИЕ
Любое комплексное число (кроме нуля) z = a
+ bi можно записать в тригонометрической
форме:
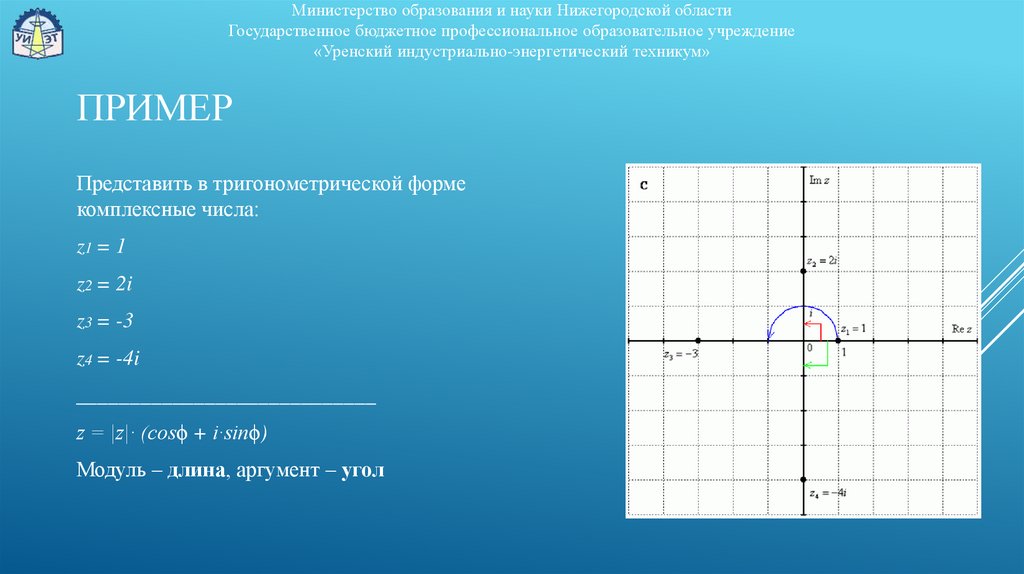
z = |z|· (cosϕ + i·sinϕ),
где |z| - это модуль комплексного числа,
а ϕ – аргумент комплексного числа
3.
Министерство образования и науки Нижегородской областиГосударственное бюджетное профессиональное образовательное учреждение
«Уренский индустриально-энергетический техникум»
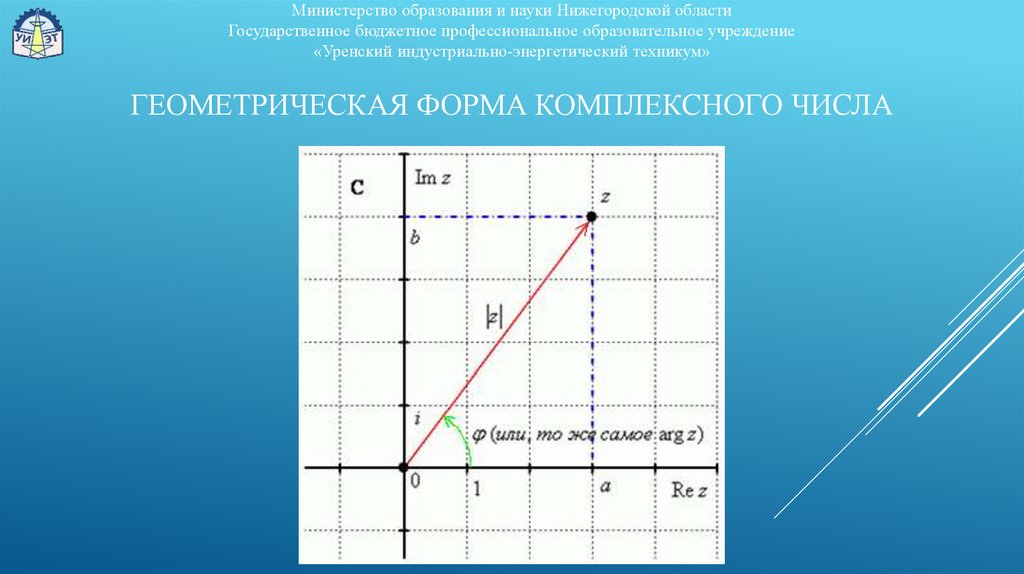
ГЕОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
4.
Министерство образования и науки Нижегородской областиГосударственное бюджетное профессиональное образовательное учреждение
«Уренский индустриально-энергетический техникум»
ОПРЕДЕЛЕНИЕ
Модулем комплексного числа z называется расстояние
от начала координат до соответствующей точки
комплексной плоскости
(модуль – это длина радиус-вектора):
| z | или r.
|z| =









 industry
industry